학생의 t-분포

학생 t

확률밀도함수
누적분포함수
매개변수	> ${\displaystyle \nu >0}$자유도(실제)
지원	$(-\displaystyle x\in (-\flatty,\flatty )}$
PDF	${\displaystyle \textstyle {\frac {\\Gamma \left({\frac {\nu +1}{2}}\오른쪽)}}{{\sqrt {\nu \pi }}\\감마 \좌({\frac {}{2}}\우)}}\좌(1+{\frac{x^{2}}}{\nu }}}^{-{\prac {\nu +1}:{2}}\}\!}$
CDF	${\displaystyle {\begin{matrix}{\frac {1}{2}}+x\Gamma \left({\frac {\nu +1}{2}}\right)\times \\[0.5em]{\frac {\,_{2}F_{1}\left({\frac {1}{2}},{\frac {\nu +1}{2}};{\frac {3}{2}};-{\frac {x^{2}}{\nu }}\right)}}{{\sqrt {\pi \nu }}}\\Gamma \left({\frac {}{nu }{2}}\오른쪽)}}}}}$ 여기서 F는1 초기하 함수다.
평균	> ${\displaystyle \nu >1}$의 경우 0 그렇지 않으면 정의되지 않음
중앙값	0
모드	0
분산	${\displaystyle \frac{\mathrm{\nu }}{}}$ - 2 ${\$ {\$nu }{\nu -2$}}:$$ > ${\displaystyle \$ >$2$ $<<\displaystyle$ 1$>[\nu$$\leq$ 2$},$ 그렇지 않으면 정의되지 않음
왜도	> ${\displaystyle \nu >3}$의 경우 0 그렇지 않으면 정의되지 않음
엑스트라 쿠르토시스	${\displaystyle \frac{}{}}$ ${\displaystyle \frac{\nu }{}}$- ${\displaystyle \frac{4}{}}$$\$$displaystyle$$\textstyle${\$frac {6}{\$$nu -4$$}$의 경우 <$≤$ $>$의 경우, 그렇지 않으면 정의되지 않음
엔트로피	${\displaystyle {\begin{matrix}{\frac {\nu +1}{2}}\left[\psi \left({\frac {1+\nu }{2}}\right)-\psi \left({\frac {\nu }{2}}\right)\right]\\[0.5em]+\ln {\left[{\sqrt {\nu }}B\left({\frac {\nu }{2}},{\frac {1}{2}}\right)\right]}\,{\scriptstyle {\text{(nats)}}}\끝{{matrix}}}$ ψ: 디감마 함수, B: 베타 함수
MGF	정의되지 않은
CF	${\displaystyle \textstyle {\frac {K_{\nu /2}\left({\sqrt {\nu }} t \right)\cdot \left({\sqrt {\nu }} t \right)^{\nu /2}}{\Gamma (\nu /2)2^{\nu /2-1}}}}$ for ${\displaystyle \nu >0}$ ${\displaystyle K_{}}$ ${\displaystyle \nu {}_{}}$( x${\displaystyle }$) ${\displaystyle K_{\nu }(x)}$: 두 번째 종류의[1] 수정된 Besel 함수

확률과 통계에서 학생의 t-분포(또는 단순히 t-분포)는 표본 크기가 작고 모집단의 표준 편차를 알 수 없는 상황에서 정규 분포 모집단의 평균을 추정할 때 발생하는 연속 확률 분포 계열의 구성원이다.영국의 통계학자 윌리엄 씰리 고셋이 '스튜디오'라는 필명으로 개발했다.

t-분포는 두 표본 평균 차이의 통계적 유의성을 평가하기 위한 학생의 t-검정, 두 모집단 평균 차이에 대한 신뢰 구간 구성 및 선형 회귀 분석에서 광범위하게 사용되는 여러 통계 분석에서 역할을 한다.학생의 t 분포는 일반 가정의 데이터에 대한 베이지안 분석에서도 발생한다.

정규 분포에서 $n{\displaystyle }$ ${\displaystyle n}$ 관측치의$$ 표본을 추출하는 경우 freedom${\displaystyle }$= ${\displaystyle \mathrm{n}}$- ${\displaystyle 1}$ ${\displaystyle \nu =n-1}$자유도가 있는 t 분포는 sta로 곱한 후 참 평균에 상대적인 표본 평균 위치의 분포로 정의할 수 있다.ndardizing 용어 ${\$ 이러한 방식으로 t-분포를 사용하여 실제 평균에 대한 신뢰 구간을 구성할 수 있다.

t-분포는 정규분포와 같이 대칭이며 종 모양이다.그러나 t 분포는 꼬리가 더 무거워 평균에서 멀리 떨어진 값을 산출하기 쉽다는 것을 의미한다.이것은 분모의 변동이 증폭되고 비율의 분모가 0에 가까울 때 외향 값을 산출할 수 있는 특정 유형의 무작위 수량 비율의 통계적 동작을 이해하는 데 유용하다.학생의 t-분포는 일반화된 쌍곡선 분포의 특별한 경우다.

역사와 어원

통계에서 t 분포는 1876년 헬머트와^[2][3][4] 뤼트로스에 의해 후분포로서 처음 도출되었다.^[5][6][7]t-분포는 칼 피어슨의 1895년 논문에서도 피어슨 4종 분포로 보다 일반적인 형태로 나타났다.^[8]

영문학에서 이 분포는 윌리엄 씰리 고셋의 1908년 비오메트리카에 실린 논문에서 '학생'^[9]이라는 필명으로 그 이름을 따왔다.고셋은 아일랜드 더블린에 있는 기네스맥주에서 일했고, 작은 표본의 문제, 예를 들어 표본 크기가 3 정도 되는 보리의 화학적 특성 등에 관심이 있었다.가명 원고의 한 버전은 고셋의 고용주가 실명 대신 과학논문을 발행할 때 직원이 필명을 사용하는 것을 선호해 '스튜던트'라는 이름을 사용해 신분을 숨겼다는 것이다.또 다른 버전은 기네스북이 경쟁자들이 원료의 품질을 결정하기 위해 t-테스트를 사용하고 있다는 사실을 알고 싶어하지 않았다는 것이다.^[10][11]

고셋의 논문은 분포를 "정상 모집단에서 추출한 표본의 표준 편차의 빈도 분포"라고 한다.그것은 로널드 피셔의 작품을 통해 잘 알려지게 되었는데, 그는 그 분포를 "학생의 분포"라고 불렀고 t자로 시험값을 나타내었다.^[12][13]

학생 분포가 표본 추출에서 발생하는 방법

Let ${\textstyle X_{1},\ldots ,X_{n}}$ be independently and identically drawn from the distribution ${\displaystyle {\mathcal {N}}(\mu ,\sigma ^{2})}$, i.e. this is a sample of size ${\displaystyle n}$ from a normally distributed population with expected mean value ${\displaysty$$\mu }$과(와) 분산 ${\displaystyle {\sigma \mathrm{}}^{}}$ 2 ${\$

내버려두다

${\displaystyle {\bar{X}={\frac {1}{n}\sum _{i=1}^{n}X_{i}}}}$

을 본보기로 삼가다

${\displaystyle S^{2}={\frac {1}{n-1}\sum _{i=1}^{n}(X_{i}-{\bar{X})^{2}}$

표본 분산이다그러면 랜덤 변수

${\displaystyle {\frac {{\bar}-\mu }{\sigma /{\sqrt{n}}}}$

표준 정규 분포(예: 기대 평균이 0이고 분산 1인 정규 분포) 및 랜덤 변수가 있음

${\displaystyle {\frac {{\bar {{X}-\mu}{S/{\sqrt{n}}}}$

즉, $S{\displaystyle }$ ${\displaystyle S}$이(가) $\sigma {\displaystyle }$ ${\displaystyle \sigma }$을(를) 대체한 경우$$$,$ 학생 t-분포가 $n{\displaystyle }$- ${\displaystyle 1}$ {\$displaystyle n-1}$ 자유도를$$ 가지고 있다.$S$ ${\textstyle S}$이(가) $\sigma$, ${\textstyle \sigma ,}$을(를) 대체했기 때문에 이 식에서 관측할 수 없는 유일한$$ 수량은 $\mu$, ${\textstyle$ $\mu ,}$이므로 이것은$$ $\mu$에 대한 신뢰 구간을 도출하는 데 사용될 수 있다$.$ ${\text$ stypot.e 동일한 샘플 $X{}_{}$ ${1\mathrm{}}_{}$,$$…$$, ${}_{}$ $n_{}$ ${\$에 기초하고 있음$.$This can be seen by observing that ${\textstyle \operatorname {cov} ({\overline {X}},\,X_{i}-{\overline {X}})=0,}$ and recalling that ${\textstyle {\overline {X}}}$ and ${\textstyle X_{i}-{\overline {X}}}$ are both linear combinations of the same set of i.i.d.정규 분포를 따르는 랜덤 변수.

정의

확률밀도함수

학생의 t-분포에는 다음과 같은 확률밀도함수(PDF)가 있다.

${\displaystyle f(t)={\frac {\Gamma ({\frac {\nu +1}{2}})}{{\sqrt {\nu \pi }}\,\Gamma ({\frac {\nu }{2}})}}\left(1+{\frac {t^{2}}{\nu }}\right)^{\!-{\frac {\nu +1}{2}}},\!}$

여기서 $\nu {\displaystyle }$ ${\displaystyle \nu}$은(는) 자유도 수이고 $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma}$은(는) 감마함수다.이것은 또한 다음과 같이 쓰여질 수 있다.

${\displaystyle f(t)={\frac {1}{{\sqrt {\nu }}\,\mathrm {B} ({\frac {1}{2}},{\frac {\nu }{2}})}}\left(1+{\frac {t^{2}}{\nu }}\right)^{\!-{\frac {\nu +1}{2}}}\!,}$

여기서 B는 베타 함수다.특히 자유도의 정수 값 $\nu {\displaystyle }${\$displaystyle \nu$}에$$ 대해서는 다음과 같은 사항을 제공한다.

> ${\displaystyle \nu >1}$의 경우에도,

${\displaystyle {\frac {\gamma({\frac {\nu +1}{2}}:}{{\\sqrt {\nu \pi }}}\\Gamma({\frac {\nu }{2}})}}}={\frac {(\nu -1)(\nu -3)\cdot 5\cdot 3}{2{\\sqrt {\nu -2)}(\nu -2)(\nu -4)\cdot 4\cdot 2\,}}$

> ${\displaystyle \nu >$1$}$홀수인 경우,

${\displaystyle {\frac {\gamma({\frac {\nu +1}{2}}:}{{\\sqrt {\nu \pi }}}\\Gamma({\frac {\nu }{2}})}}}={\frac {(\nu -1)(\nu -3)\cdots 4\cdot 2}{\pi {\sqrt {\nu -2)(\nu -2)(\nu -4)\cdot 5\cdot 3\,}\cdot \!}$

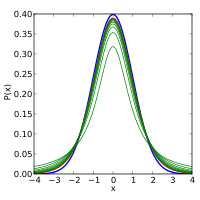
확률밀도함수는 대칭이며, 그 전체적인 모양은 약간 낮고 넓다는 점을 제외하고는 평균 0과 분산 1의 정규 분포 변수의 종 모양과 유사하다.자유도가 증가함에 따라 t 분포는 평균 0과 분산 1로 정규 분포에 접근한다.이 때문에 ${\$은(는) 정규성 파라미터로도 알려져 있다.^[14]

다음 이미지는 $\nu {\displaystyle }$ ${\displaystyle \nu }$의 증가 값에 대한 t 분포의 밀도를 보여준다$.$ 정상 분포는 비교를 위해 파란색 선으로 표시된다.t-분포(빨간색 선)는 $\nu {\displaystyle }$ ${\displaystyle \nu }$이(가) 증가함에 따라 정규 분포에 가까워진다는 점에 유의하십시오.

누적분포함수

누적분포함수(CDF)는 정규화된 불완전 베타함수인 I로 작성할 수 있다.t > 0의 경우,^[15]

${\displaystyle F(t)=\int _{-\not}^{t}f(u)\,du=1-{\tfrac {1}{2}}I_{x(t)}\좌측({\tfrac {}{{nu{2}},{\tfrac {1},{1}, 우측)}}$

어디에

${\displaystyle x(t)={\frac {\nu }{t^{2}+\nu }}.}$

다른 값들은 대칭으로 얻을 수 있을 것이다. < ${\displaystyle t^{2}<\nu$ 에 유효한 대체 공식은 다음과^[15] 같다.

${\displaystyle \int _{-\nu +1)^{t}f(u)\,du={\tfrac{1}{1}:{1}2}}+t{\prac {\Gamma \좌({\tfrac {1}{1}{1}{2}}(\nu +1)\오른쪽)}{{\sqrt {\pi \nu }}\,\Gamma \left({\tfrac {\nu }{2}}\right)}}\,{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}}(\nu +1);{\tfrac {3}{2}};-{\tfrac {t^{2}}{\nu }}\right),}$

여기서 F는₁ 초기하 함수의 특별한 경우다.

역 누적 분포 함수에 대한 자세한 내용은 § 학생의 t-분포를 참조하십시오.

특례

$\nu {\displaystyle }$ ${\displaystyle \nu}$의 특정 값은 특히 단순한 형태를 나타낸다$$.

• ${\displaystyle \nu =1}$

분포 함수:

${\displaystyle F(t)={\tfrac {1}{2}}+{\tfrac {1}{\pi }}}\arctan(t).}$

밀도 함수:

${\displaystyle f(t)={\frac {1}{\pi(1+t^{2})}}.}$

Cauchy 분포 참조

• $\displaystyle \nu =2}$

분포 함수:

${\displaystyle F(t)={\tfrac {1}{1}:{2}}+{{2}{\prac {t}{2}{\sqrt{1}{1+{t^{2}}}}}}}}.}$

밀도 함수:

${\displaystyle f(t)={\frac {1}{2{\\sqrt{2}}:}\왼쪽(1+{\frac{t^{2}}:\오른쪽)^{\frac {3}}}.}$

• $\displaystyle \nu =3}$

분포 함수:

${\displaystyle F(t)={\frac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {1}{\sqrt {3}}}{\frac {t}{1+{\frac {t^{2}}{3}}}}+\arctan \left({\frac {t}{\sqrt {3}}}\right)\right]}.}$

밀도 함수:

${\displaystyle f(t)={\frac {2}{\pi {\sqrt{3}}\왼쪽(1+{\frac{t^{2}}:{3}\오른쪽)^{2}}.}$

• $\displaystyle \nu =4}$

분포 함수:

${\displaystyle F(t)={\tfrac {1}{2}}+{\frac {3}{8}}{\frac {t}{\sqrt {1+{\frac {t^{2}}{4}}}}}{\left[1-{\frac {1}{12}}{\frac {t^{2}}{1+{\frac {t^{2}}{4}}}}\right]}.}$

밀도 함수:

${\displaystyle f(t)={\frac {3}{8\좌측(1+{\frac{t^{2}}:{4}\우측)^{\frac {5}{2}}.}$

• $\displaystyle \nu =5}$

분포 함수:

${\displaystyle F(t)={\tfrac {1}{2}}+{\frac {1}{\pi }}{\left[{\frac {t}{{\sqrt {5}}\left(1+{\frac {t^{2}}{5}}\right)}}\left(1+{\frac {2}{3\left(1+{\frac {t^{2}}{5}}\right)}}\right)+\arctan \left({\frac {t}{\sqrt {5}}}\right)\right]}.}$

밀도 함수:

${\displaystyle f(t)={\frac {8}{3\pi {\sqrt{5}\{5}}\좌측(1+{\frac{t^{5}}}{5}\우측)^{3}}}.}$

• $\displaystyle \nu =\flotty }$

분포 함수:

${\displaystyle F(t)={\frac {1}{1}{2}}: {\좌측[1+\operatorname {erf} \좌측({\frac {t}{\sqrt {2}}\우측)\우측]}}}}.}$

오류 함수 참조

밀도 함수:

${\displaystyle f(t)={\frac {1}{\\sqrt{2\pi }}e^{-{\frac{t^{2}}.}$

정규 분포를 참조하십시오.

t-분포 발생 방법

시료채취분포

$x{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}\cdots ,}$ ${\displaystyle {}_{}}$ ${\displaystyle n_{}}$ ${\$을(를) 예상 값 ${\displaystyle \mu }$을(를) 가진 연속 분포 모집단에서 표본에서 관측된 숫자로 한다$$$.$ 표본 평균과 표본 분산은 다음과 같이 주어진다.

${\displaystyle {\i1}{x}&={\frac {x_{1}+\cdots +x_{n}}{n}},\s^{n}&={n1}{n-1}\sum _{i=1}^{n}(x_{x}-})^{2}}.\end{정렬}}}$

결과 t-값은

${\displaystyle t={\frac {{\bar {{x}-\mu }{s/{\sqrt{n}}}.}$

자유도가$$ $n{\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle n-1}$인 t 분포는 표본이 정규 분포 모집단에서 동일한 독립 분포 관측치로 구성되었을 때 t-값의 표본 분포다.따라서 추론 목적상 t는 평균과 분산$({\displaystyle \mu }$ ,${\displaystyle {\mu \mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) ${\displaystyle (\mu ,\sigma ^{2})$이 미지의 모집단 매개변수인 경우에 유용한 "양"으로, t-값이 $\mu {\displaystyle }$ ${\displaystyle \mu$ \mu$$}, $\$에 의존하지 않는 확률 분포를 가진다.$시그마 ^{2$

베이시안 추론

베이시안 통계량에서 (확대, 이동) t 분포는 알 수 없는 분산에 대한 의존성이 한계화된 경우 정규 분포의 미지의 평균에 대한 한계 분포로 발생한다.^[16]

${\displaystyle {\begin{aligned}p(\mu \mid D,I)=&\int p(\mu ,\sigma ^{2}\mid D,I)\,d\sigma ^{2}\\=&\int p(\mu \mid D,\sigma ^{2},I)\,p(\sigma ^{2}\mid D,I)\,d\sigma ^{2},\end{aligned}}}$

여기서 $D{\displaystyle }$ ${\displaystyle D}$은(는) 데이터${\displaystyle }${${\displaystyle {xi}_{}}$}$${\$displaystyle$\{$x_{i$을(를) 나타내며$$, $I{\displaystyle }$ ${\displaystyle I}$은 모델을 생성하는 데 사용되었을 수 있는 다른 모든 정보를 나타낸다.따라서$$ 분포는 $데이터$가 주어진$\mu s$의 조건부 분포 {\$displaystyle \mu$}과 ${\displaystyle {데이터}^{}}$가 ${\displaystyle {주어진\mathrm{}}^{}}$ μs$$2 {\$displaystyle$$$\$sigma ^{$2}}의 한계 분포가 합쳐진 것이다$.$

n{n\displaystyle}데이터 지점을 사용하는 경우, 또는 평평한, 위치와 규모 충분한 전과}}과(σ 2∣ 나는)∝ 1/σ 2{\displaystyle p(\sigma ^{2}\mid 나는)\propto 1/\sigma ^{2}}과 σ2μ에 하든지 베이즈 정리의 giv으로 여겨질 수 있는 동업-(μ ∣ σ 2, 나는))const{\displaystyle p(\mu\mid \sigma ^{2},I)={\text{const}p.es

${\displaystyle {\begin{aligned}p(\mu \mid D,\sigma ^{2},I)&\sim N({\bar {x}},\sigma ^{2}/n),\\p(\sigma ^{2}\mid D,I)&\sim \operatorname {Scale-inv-} \chi ^{2}(\nu ,s^{2}),\end{aligned}}}$

정규 분포와 스케일 역치-제곱 분포 각각${\displaystyle ,}$ $여기$서 ${\displaystyle n}$= ${\displaystyle \mathrm{n}}$ -$$1 {\$displaystyle \nu$ =$n-1}$ 및

${\displaystyle s^{2}=\sum {\frac {(x_{i}-{\bar{x}})^{2}}{n-1}.}$

따라서 한계화 적분은

${\displaystyle{\begin{정렬}(\mu \mid D,I)&,\propto \int _{0}^{\infty}{\frac{1}{\sqrt{\sigma ^{2}}}}\exp \left(-{\frac{1}{2\sigma ^{2}}}n(\mu-{\bar{x}})^{2}\right)\cdot \sigma ^ᆱ\exp(-\nu s^{2}/2\sigma ^{2})\,d\sigma ^{2}\\&, \propto\int _{0}^{\infty}\sigma ^{-\nu-3}\exp \left(-{\frac{1}{2\sigma ^{2}}}\left(n(\mu-{\bar{.x}})^{2}+\nu s^{2}\오른쪽)\,d\bma ^{2}.\end{정렬}}}$

$이것$은 z${\displaystyle }$= ${\displaystyle A}$/ 2 ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$${\displaystyle A}$$/2\sigma ^{2$ $여기$서 A${\displaystyle }$= n${\displaystyle }$(${\displaystyle \mu }$- ${\displaystyle x\stackrel{}{}}$μ - x )${\displaystyle {}^{2\mathrm{}}}$+ ${\displaystyle \nu }$ s ${\displaystyle {2\mathrm{}}^{}}$ ${\$ -${bar{x}})^{2}+\nu$ s$^2}},$ 주어$$평가한다.

${\displaystyle dz=-{\frac {A}{2\sigma ^{4}}\,d\sigma ^{2},}$

그렇게

${\displaystyle p(\mu \mid D,I)\propto A^{-{-{\frac {\nu +1}{2}}\int_{0}^{{0}{\nu -1)/2} exp(-z)\,dz.}$

그러나 z 적분은 이제 표준 감마 적분으로, 상수로 평가하여 남는다.

${\displaystyle {\begin{aligned}p(\mu \mid D,I)&\propto A^{-{\frac {\nu +1}{2}}}\\&\propto \left(1+{\frac {n(\mu -{\bar {x}})^{2}}{\nu s^{2}}}\right)^{-{\frac {\nu +1}{2}}}.\end{정렬}}}$

이는 명시적 스케일링과 시프트가 있는 t-분포의 한 형태로서, 아래 추가 섹션에서 자세히 살펴볼 것이다.대체에 의한 표준화된 t-분포와 관련될 수 있다.

${\displaystyle t={\frac {\mu -{\bar{x}}{s/{\sqrt{n}}}.}$

위의 도출은 $[\displaystyle \mu }$ 및$$ ${\displaystyle {\mu \mathrm{}}^{}}$ 2$[\$에 대한 비정보적 사전의 경우에 대해 제시되었지만, 정상 분포를 스케일 역치 제곱 분포와 조합하게 하는 모든 사전 분포는 스케일 및 시 분포를 포함한 t-분포를 야기할 것이 명백하다$.$$위$의 ${\displaystyle \frac{{}^{}}{}}$ ${\$}에 해당하는 스케일링 $파라미터$는 위의 데이터뿐만 아니라 이전 정보와 데이터 모두에 의해 영향을 받지만 P$($${\displaystyle \mu }$ D ,${\displaystyle I}$) ${\mu \mid D,I$$}$에 대한 fting.

특성화

검정 통계량의 분포로서

$degrees{\displaystyle }$ ${\displaystyle \nu }$자유도를$$ 가진 학생의 t 분포는 다음 값을^[15][17] 가진 랜덤 변수 T의 분포로 정의할 수 있다.

${\displaystyle T={\frac {Z}{\sqrt {V/\nu}}}=Z{\sqrt {\frac {}{V}}}},}$

어디에

• Z는 기대값이 0이고 분산이 1인 표준 정규 분포를 따른다.
• V에는 자유도가 ${\displaystyle \nu }$인 카이-제곱 분포(분포²)가 있다.
• Z와 V는 독립적이다.

다른 분포는 주어진 일정한 μ에 대해 정의된 랜덤 변수의 분포로 정의된다.

${\displaystyle(Z+\mu ){\sqrt {\frac {\nu}{V}}.}$

이 랜덤 변수는 비중심 t-분포를 가지며 비중심 파라미터 μ를 가진다.이 분포는 학생 t-검사의 힘에 대한 연구에서 중요하다.

파생

X₁, ..., X가_n 정규 분포를 따르는 임의 변수 X의 독립적 실현이라고 가정해 보자. X는 기대값 μ와 분산 μ를² 가지고 있다.내버려두다

${\displaystyle {\overline{X}_{n}={\frac {1}{n1}(X_{1}+\cdots +X_{n})}$

표본의 평균이다, 그리고

${\displaystyle S_{n}^{n2}={\frac {1}{n-1}\sum _{i=1}^{n}\좌측(X_{i}-{\overline {X}_{n}\오른쪽)^{2}}$

표본의 분산을 편파적으로 추정하다랜덤 변수가

${\displaystyle V=(n-1){\frac {S_{n}^{2}}:{\sigma ^{2}}:$

$\nu {\displaystyle }$= ${\displaystyle \mathrm{n}}$- 1 ${\displaystyle \nu =n-1}$ 자유도를$$ 갖는 카이 제곱 분포를 가진다(^[18]코크란의 정리).그 수량은 쉽게 알 수 있다.

${\displaystyle Z=\왼쪽({\overline {X}_{n}-\mu \right){\frac {\sqrt{n}{\sigma}}}}$

표본 평균 $X$의${\displaystyle {\stackrel{}{}n}_{}}$ ${\$은(는) 평균 μ와 분산 σ²/n으로 정규 분포되기 때문에 평균 0과 분산 1로 정규 분포를 따른다.더욱이 이러한 두 개의 랜덤 변수(정상적으로 분포된 Z와 카이-제곱 분포된 V)가 독립적이라는 것을 보여줄 수 있다.결과적으로^{[clarification needed]} 중추적인 수량

${\textstyle T\equiv {\z}{\sqrt {V/\nu}}}}=\좌측({\overline {X}_{n}-\mu \right){\frac {\sqrt{n}}}}, {\sqrt}, {\s_{n}}}}}},},},},},},},$

이는 정확한 표준 편차 σ이 무작위 변수_n S로 대체된다는 점에서 Z와 다른 점이며, 위에서 정의한 학생 t-분포를 가지고 있다.알 수 없는 모집단 분산 σ은² 분자와 분모 둘 다에 있어서 취소하였으므로 T에는 나타나지 않는다는 점에 유의한다.고셋은 직관적으로 위에서 말한 확률밀도함수를 n - 1과 같은 equal$$ ${\displaystyle \nu }$로 얻었고, 피셔는 1925년에 그것을 증명했다.^[12]

시험통계 T의 분포는 $\mu$나 μ는 아니지만$$μ는$$\$displaystyle \nu }$에 따라 달라진다. μ와 μ는 μ와 μ에 대한 의존도의 부족이 이론과 실제 모두에서 t-분포를 중요하게 만든다.

최대 엔트로피 분포로서

학생의 t-분포는 $E{\displaystyle \mathrm{}(\ln }$ ${\displaystyle }$ (${\displaystyle \nu }$ + ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$)${\displaystyle \operatorname {E}(\ln(\nu +X^{2}))$이 고정된$$ 임의 변수 X에 대한 최대 엔트로피 확률 분포다.^{[19][clarification needed][better source needed]}

특성.

순간

> 1 ${\displaystyle \nu >1}$의 경우t-분포의 원시 모멘트는

${\displaystyle \operatorname {E} (T^{k})={\begin{cases}0&k{\text{ odd}},\quad 0<k<\nu \\{\frac {1}{{\sqrt {\pi }}\Gamma \left({\frac {\nu }{2}}\right)}}\left[\Gamma \left({\frac {k+1}{2}}\right)\Gamma \left({\frac {\nu -k}{2}}\오른쪽)\nu ^{\frac {1}{2}}\오른쪽]&k{\text{ven}},\quad 0<\nu.\\end{case}}$

$moments{\displaystyle }$ ${\displaystyle \nu}$ 이상 주문$$ 모멘트가 존재하지 않음.^[20]

< < ${\displaystyle 0<\k<\nu},$ 짝수의 용어는 감마함수의 속성을 사용하여 다음과 같이 단순화할 수 있다.

${\displaystyle \operatorname {E}(T^{k})=\nu ^{\frac {k}{2}}\,\prod_{i=1}^{k/2}}{\frac {2i-1}{\nu -2}}\qquad k{{ven},\quad 0<k\nu.}}$

$\nu {\displaystyle }$ ${\displaystyle \nu$$}$자유도가$$ 있는 t 분포의 경우 은 ${\displaystyle \nu >1}$이면 0이고 > 2 ${\$ -2$}}$인 경우$$ 분산은 ${\displaystyle \frac{\nu }{}}$ -${\displaystyle \frac{2}{}}$ ${\displaystylean \nu$ >$2}$이다wn> ${\displaystyle \nu >3}$이면 왜도가 0이고, 초과 첨도는 6 ${\displaystyle \frac{\mathrm{\nu }}{}}$- 4 ${\displaystyle$ {6$}{\nu -4},$ > ${\displaystyle \nu >4}$이다

몬테카를로 샘플링

학생의 t-분포에서 무작위 샘플을 만드는 방법은 다양하다.문제는 표본이 독립적으로 필요한지, 또는 균일한 표본에 정량적 함수를 적용하여 시공해야 하는지에 따라 달라진다(예: 코풀라 의존성의 다차원적 적용 기준).^{[citation needed]}독립형 표본 추출의 경우 Box-Muller 방법의 확장 및 극형 형태가 쉽게 배치된다.^[21]모든 진짜 양의 자유도인 ν에 동등하게 잘 적용되는 반면, ν이 0에 가까우면 다른 많은 후보 방법이 실패한다는 장점이 있다.^[21]

학생의 확률밀도함수와 p-값의 정수

함수 A(t ν)는 t ≥ 0에 대한 학생 확률밀도함수의 정수인 -t와 t 사이의 f(t)이다.따라서 관측된 데이터에서 계산된 값보다 작은 값이 우연히 발생할 확률을 제공한다.따라서 두 데이터 세트를 동일한 모집단에서 추출한 경우 t의 해당 값과 발생 확률을 계산하여 두 데이터 집합의 평균 간 차이가 통계적으로 유의한지 여부를 검정할 때 A(t ν) 함수를 사용할 수 있다.이것은 다양한 상황에서 특히 t-테스트에서 사용된다.통계 t의 경우, 자유도가 ∆인 경우, A(t ν)는 두 평균이 같을 경우 t가 관측값보다 작을 확률이다(더 작은 평균을 더 큰 평균에서 빼서 t ≥ 0을 얻는 경우).t-분포의 누적분포함수 F_ν(t)로 쉽게 계산할 수 있다.

${\displaystyle A(t\mid \nu )=F_{\nu }-F_{\nu }=1-I_{\nu }{\nu +t^{2}}}\왼쪽 \frac {\nu }{2}},{\frac {1}{2}}\오른쪽),}$

여기서 나는_x 정규화된 불완전 베타 함수(a, b)이다.

통계적 가설 검정에서 이 함수는 p-값을 구성하는 데 사용된다.

일반화 학생의 t-분포

$스케일링$ 파라미터 ^ $^$ {\$displaystyle${\$hat {\sigma }$ 또는 ^ ${\displaystyle {\stackrel{}{^}}^{}}$ ${\displaystyle 2^{\mathrm{}}}$ ${\$

학생의 t 분포는 위치 모수 $\mu {\displaystyle \hat{}}$ {\$displaystyle {\mu$}}과(와$)$ 관계를$$ 통해 $위치{\displaystyle \stackrel{}{}}$ 모수 μ${\displaystyle \stackrel{}{^}}$ ${\$을$($를) 도입하여 세 가지 모수 위치 척도 패밀리로 일반화할 수 있다.

${\displaystyle X={\hat{\mu }}+{\hat {\sigma }T}$

또는

${\displaystyle T={\frac {X-{\hat{\mu }}{\hat {\sigma }}}{\hat {\sigma }}}}}}}}}$

이는 $x{\displaystyle \frac{}{}}$ -${\displaystyle \frac{\mu }{\stackrel{}{}}}$ $^$ ^ ${\displaystyle \frac{\stackrel{}{^}}{}}$ ${\$$hat$${\$$sigma$}}}}}}}}}}}}}}}이(가) $자유도$인$$고전적인 학생 t 분포를 가지고 있음을$$ 의미한다.

결과적으로 비표준화된 학생의 t-분포는 다음과 같이 정의된다.^[22]

${\displaystyle p(x\mid \nu ,{\hat {\mu }},{\hat {\sigma }})={\frac {\Gamma ({\frac {\nu +1}{2}})}{\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu }}{\hat {\sigma }}\,}}\left(1+{\frac {1}{\nu }}\left({\frac {x-{\hat {\mu }}}{\hat {\sigma }}}\right)^{2}\right)^{-{\frac {\nu +1}{2}}}}$

여기서 $\sigma {\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$은(는) 표준 편차에 해당하지 않는다$$. 이는 존재하지도 않을 수 있는 스케일링 t 분포의 표준 편차가 아니며, 알 수 없는 기본 정규 분포의 표준 편차도 아니다.${\displaystyle \stackrel{}{\sigma }}$ ${\displaystyle \stackrel{}{^}}$ ${\$은(는) 단순히 분포의 전체 스케일링을 설정하십시오.위의$$ 알려지지 않은 정규 평균 $\mu {\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$의 한계 분포에 대한 베이시안 파생에서 여기서 $사용$되는 ^ ${\displaystyle \stackrel{}{^}}$ ${\$ ${\$$hat {\sigma}}}}$은$($는) $s{\displaystyle }$/ ${\displaystyle n\sqrt{}}$ ${\$ {$s/{\s}}}}}}}}}}}$에 해당한다.

${\displaystyle s^{}}$ ${\displaystyle {2\mathrm{}}^{}}$= ${\displaystyle \sum \frac{}{}}$( ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{i\stackrel{}{}{}_{}}{}}$- x ${\displaystyle \frac{\stackrel{}{""}{}^{}}{}}$) ${\displaystyle \frac{\mathrm{2n}}{}}$- 1 $displaystyle s^{2}=\sum {\frac {(x_{i}-{\bar{x}}})^{2}}{n-1$

동등하게 분포는 $다음$과 같은 척도 모수의 제곱인 $,$ ${\displaystyle {\stackrel{}{^}}^{}}$ ${\displaystyle 2^{\mathrm{}}}$ ${\$

${\displaystyle p(x\mid \nu ,{\hat {\mu }},{\hat {\sigma }}^{2})={\frac {\Gamma ({\frac {\nu +1}{2}})}{\Gamma ({\frac {\nu }{2}}){\sqrt {\pi \nu {\hat {\sigma }}^{2}}}}}\left(1+{\frac {1}{\nu }}{\frac {(x-{\hat {\mu }})^{2}}{{\hat {\sigma }}^{2}}}\right)^{-{\frac {\nu +1}{2}}}}$

이 버전의 배포의 다른 속성은 다음과 같다.^[22]

${\displaystyle {\begin{aligned}\operatorname {E} (X)&={\hat {\mu }}&{\text{ for }}\nu >1\\\operatorname {var} (X)&={\hat {\sigma }}^{2}{\frac {\nu }{\nu -2}}&{\text{ for }}\nu >2\\\operatorname {mode} (X)&={\hat {\mu }}\end{aligned}}}$

이$$ 분포는 가우스 분포(정규 분포)를 평균$\mu {\displaystyle }$ {\$displaystyle \mu }$과(와$)$ $알{\displaystyle }$ 수 없는 분산으로 혼합하여 얻으며, 역 감마 분포는 $모수{\displaystyle a}$ =${\displaystyle {\stackrel{}{}}^{}}$${\displaystyle /}$${\displaystyle {}^{}}$/ ${\displaystyle 2^{\mathrm{}}}$$$${\displaystyle$ a$=\nu {\hat {\sigma }}^{{}}}}}$$2}/2$ 즉, 랜덤 변수 X는 알 수 없는 분산이 역 감마선으로 분포된 가우스 분포를 갖는 것으로 가정하고, 그 다음 분산이 소외된다(통합 아웃).이 특성화의 유용성은 역 감마 분포가 가우스 분포의 분산의 사전 결합 분포이기 때문이다.결과적으로, 표준화되지 않은 학생의 t-분포는 많은 베이시안 추론 문제에서 자연스럽게 발생한다.아래 내용 참조.

동등하게, 이 분포는 $가우스{\displaystyle }$ 분포를$$scaled {\$displaystyle \nu$} $및$ ^${\displaystyle {\stackrel{}{}}^{}}$^ ${\displaystyle 2^{\mathrm{}}}${\$displaystyle${\$hat{\sigma$}}:{2$\}\}:$ 축척-반전-치-제곱 분포로 합성하여 얻는다.스케일-인버스-치-스퀘어 분포는 역 감마 분포와 정확히 동일한 분포지만, 매개변수화가 다른 경우${\displaystyle ,}$ 즉 ${\displaystyle 2}$ =${\displaystyle }$2 ${\displaystyle a{\stackrel{}{}}^{}}$,${\displaystyle {\stackrel{}{}2}^{\mathrm{}}}$ ${\displaystyle 2\frac{}{}}$ = ${\displaystyle \frac{b}{}}$ ${\$= $2a,\\\\\hat{\sigma }^{2}={\frac {b}{a$

이 버전의 t-분포는 재무 모델링에 유용할 수 있다.예를 들어 플라텐과 시도로위츠는 일반화된 쌍곡선 분포의 계열 중에서 약 4도의 자유도를 갖는 t-분포의 형태가 많은 전 세계 주식 지수의 (로그) 수익에 가장 적합하다는 것을 발견했다.^[23]

역 스케일링 모수 λ

역 스케일링 매개 변수 ${\displaystyle \lambda$}(정밀도가 분산의 역수인 방식과 유사함)$$에 대한 대체 매개 변수 $\lambda {\displaystyle }$= 1 ${\displaystyle \frac{{\stackrel{}{}}^{}}{}}$ ${\displaystyle \frac{{\stackrel{}{^}}^{}}{}}$ ${\displaystyle \frac{2^{\mathrm{}}}{}}$ $displaystyle \lambda ={\1}{\hat{}}{\hat$ 농도:^[24]

${\displaystyle p(x\mid \nu ,{\hat {\mu }},\lambda )={\frac {\Gamma ({\frac {\nu +1}{2}})}{\Gamma ({\frac {\nu }{2}})}}\left({\frac {\lambda }{\pi \nu }}\right)^{\frac {1}{2}}\left(1+{\frac {\lambda (x-{\hat {\mu }})^{2}}{\nu }}\right)^{-{\frac {\nu +1}{2}}}.}$

이 버전의 배포의 다른 속성은 다음과 같다.^[24]

${\displaystyle {\begin{aligned}\operatorname {E} (X)&={\hat {\mu }}&&{\text{ for }}\nu >1\\[5pt]\operatorname {var} (X)&={\frac {1}{\lambda }}{\frac {\nu }{\nu -2}}&&{\text{ for }}\nu >2\\[5pt]\operatorname {mode} (X)&={\hat {\mu }}\end{aligned}}}$

이 분포는 가우스 분포와 평균 $\mu {\displaystyle \hat{}}$ ${\$ 및 알$$ 수 없는 정밀도(분산의 역수)를 곱한 결과, 감마 ${\displaystyle \mathrm{분포}}$는 모수 $a{\displaystyle }$=$$ $/$ 2 {\$displaystyle$ a$=\$$nu$ /2} 및 b = ${\displaystyle \nu }$ /${\displaystyle }$($2λ$ )${\displaystyparm)$로 정밀도형 b$=b.$$bda )}.$즉, 랜덤 변수 X는 알 수 없는 정밀도가 감마선으로 분포된 정규 분포를 갖는 것으로 가정하고, 그 다음 감마 분포에 대해 한계화된다.

관련 분포

• If ${\displaystyle X}$ has a Student's t-distribution with degree of freedom ${\displaystyle \nu }$ then X² has an F-distribution: ${\displaystyle X^{2}\sim \mathrm {F} \left(\nu _{1}=1,\nu _{2}=\nu \right)}$
• 비중앙 t-분포는 위치 파라미터를 포함하도록 t-분포를 일반화한다.비표준화된 t-분포와 달리 비중심 분포는 대칭이 아니다(중위값이 모드와 같지 않음).
• 이산 학생의 t-분포는 r:에 비례하는 확률 질량 함수로 정의된다.^[25]

${\displaystyle \prod _{j=1}^{k}{\frac {1}{(r+j+a)^{2}+b^{2}}}\cHB \dots r=\ldots,-1,\dots .}$

여기서 a, b, k는 변수다.이 분포는 연속 분포에 대한 Pearson 분포와 유사한 이산 분포 시스템의 구성에서 발생한다.^[26]

• 정규 분포와 χ-분포의² 제곱근에서 변수의 비율을 취함으로써 Student-t 표본을 생성할 수 있다.예를 들어 어윈-홀 분포와 같은 정규 분포 대신 사용할 경우 정규 분포, 유니폼 분포, 삼각 분포, 학생 분포 및 카우치 분포가 포함된 대칭 4-모수 분포를 전체적으로 얻는다.이것은 정규 분포의 다른 대칭 일반화보다 더 유연하다.
• t-평균은 비율 분포의 한 예다.

사용하다

빈번한 통계적 추론에서.

학생의 t-분포는 데이터가 부가오류로 관측되는 환경에서 평균값과 같은 미지의 모수를 추정하는 것을 목적으로 하는 다양한 통계적 추정 문제에서 발생한다.(거의 모든 실제 통계 작업에서와 마찬가지로) 이러한 오류의 모집단 표준 편차를 알 수 없고 데이터로부터 추정해야 하는 경우, t 분포는 종종 이 추정에 따른 추가 불확실성을 설명하기 위해 사용된다.대부분의 그러한 문제에서 오차의 표준 편차를 알면 t-분포 대신 정규 분포를 사용하게 된다.

신뢰구간과 가설검사는 특정 통계량의 표본분포(예: 표준점수)의 정량적 분포를 요구하는 두 가지 통계적 절차다.이 통계가 데이터의 선형 함수인 모든 상황에서, 표준 편차의 일반적인 추정치로 나눈 결과 수량의 크기를 조정하고 학생의 t-분포를 따르도록 중심을 맞출 수 있다.평균, 가중 평균 및 회귀 계수를 포함하는 통계 분석은 모두 이러한 형태를 갖는 통계로 이어진다.

교과서 문제는 모집단 표준 편차를 알고 있는 것처럼 취급하여 학생의 t-분포를 사용할 필요가 없는 경우가 꽤 많다.이러한 문제들은 일반적으로 (1) 표본 크기가 너무 커서 분산의 데이터 기반 추정치를 확실한 것처럼 취급할 수 있는 문제들과 (2) 표준 편차 추정 문제가 autho가 아닌 점이기 때문에 일시적으로 무시되는 수학 추론을 설명하는 문제들이다.r 또는 강사가 설명하고 있다.

가설 검정

관심 있는 귀무 가설에서 중간 크기의 표본에 대해 t-분포를 갖는 여러 통계량을 보여줌으로써 t-분포가 유의성 검정의 기초를 형성한다.예를 들어, Spearman의 순위 상관 계수 ρ의 분포는 null의 경우(상관 0)가 약 20개 이상의 표본 크기에 대한 t 분포에 의해 잘 근사하다.^{[citation needed]}

신뢰구간

A라는 숫자가 너무 선택되어 있다고 가정하자.

${\displaystyle \Pr(-A<T>=0.9,}$

T가 자유도가 n - 1인 t-분포를 갖는 경우.대칭적으로 이것은 A가 만족한다고 말하는 것과 같다.

${\displaystyle \Pr(T<A)=0.95,}$

그래서 A는 이 확률 분포의 "95번째 백분위수" 또는 $A{\displaystyle }$= ${\displaystyle {}_{}}$(${\displaystyle {0.05}_{}}$,${\displaystyle n_{}}$- ${\displaystyle 1_{}}$ $){\$ 그러면

${\displaystyle \Pr \left(-A<{\frac {{\overline{X}_{n}-\mu}{\frac {S_{n}}}{\sqrt{n}}}}}}}}}{\sqrt{n}}}}}<A\rig)=0.9,}$

그리고 이것은 에 해당한다.

${\displaystyle \Pr \left({\overline {X}_{n}-A{\prac {S_{n}}}}<\mu <{\overline {X}_{n}}}+)A{\frac{S_{n}}{\sqrt{n}}\오른쪽)=0.9.}$

따라서 엔드포인트가 있는 간격

${\displaystyle {\overline{X}_{n}\pm A{\frac {S_{n}}{\sqrt{n}}}}}$

μ에 대한 90% 신뢰 구간.따라서, 우리가 합리적으로 정규 분포를 가질 것으로 예상할 수 있는 관측치 집합의 평균을 발견하면, t-분포를 사용하여 해당 평균에 대한 신뢰 한계가 귀무 가설에서 예측된 값과 같이 이론적으로 예측된 값을 포함하는지 여부를 조사할 수 있다.

학생의 t 검정에 사용되는 이 결과: 두 정규 분포에서 표본 평균의 차이 자체가 정규 분포를 따르므로 t-분포를 사용하여 해당 차이가 0으로 합리적으로 가정할 수 있는지 여부를 조사할 수 있다.

데이터가 정규 분포를 따르는 경우 평균의 단측(1 - α)-상측 신뢰 한계(UCL)는 다음 방정식을 사용하여 계산할 수 있다.

${\displaystyle \mathrm{UCL} _{1-\alpha }={\overline{X}}+t_{\alpha,n-1}{\frac {S_{n}}{\sqrt{n}}}.}$

결과 UCL은 주어진 신뢰 구간과 모집단 크기에 대해 발생하는 가장 큰 평균 값이 될 것이다.즉 ${\displaystyle X_{}}$의${\displaystyle {\stackrel{}{}}_{}}$n ${\$은 관측치$$ 집합의 평균으로, 분포의 평균이 UCL보다_1−α 낮을 확률은 신뢰수준 1 - α와 같다.

예측 구간

t-분포는 평균과 분산을 알 수 없는 정규 분포에서 관측되지 않은 표본에 대한 예측 구간을 구성하는 데 사용할 수 있다.

베이지안 통계학

학생의 t-분포는 특히 3-모수(위치-척도) 버전에서 정규분포와 연관된 결과로 베이시안 통계에서 자주 발생한다.정규 분포 랜덤 변수의 분산을 알 수 없고 역 감마 분포를 따르는 결합 전 배치될 때마다 변수의 결과 한계 분포는 학생의 t 분포를 따를 것이다.동일한 결과를 갖는 등가 구조에는 분산에 대한 결합 축척-반향-치 제곱 분포 또는 정밀도에 대한 결합 감마 분포가 포함된다.σ에⁻² 비례하는 부적절한 사전 비율이 분산 위에 놓이면 t-분포도 발생한다.정규 분포 변수의 평균을 알 수 있는지, 이전에 정규 분포된 공극에 따라 알 수 없는지, 또는 이전의 부적절한 상수에 따라 알 수 없는 것인지에 관계없이 이 경우다.

t-분포를 발생시키는 관련 상황은 다음과 같다.

• 정규 분포 변수의 알 수 없는 평균의 한계 후방 분포로, 위의 모형에 따른 알 수 없는 이전 평균과 분산이 있다.
• 위의 모델과 같이 이전 평균과 분산을 사용하여 동일한 분산된 일련의 독립적 정규 분포 데이터 점이 관찰된 경우 새로운 정규 분포 데이터 포인트의 사전 예측 분포 및 후방 예측 분포.

강력한 파라메트릭 모델링

t-분포는 종종 데이터에 대한 모델로서 정규 분포의 대안으로 사용되는데, 이는 종종 정규 분포가 허용하는 것보다 더 무거운 꼬리를 가지고 있다(예: 참조).랜지 ^[27]외고전적인 접근방식은 특이치를 식별하고(예: 그루브스 검정을 사용) 어떤 식으로든 이를 배제하거나 저체중화하는 것이었다.그러나 특이치를 식별하는 것이 항상 쉬운 것은 아니며(특히 높은 치수에서), t-분포는 그러한 데이터에 대한 자연스러운 모델 선택이며 강력한 통계량에 대한 파라메트릭 접근법을 제공한다.

베이시안 계정은 겔만 등지에서 찾을 수 있다.^[28]자유도 모수는 분포의 첨도를 제어하며 척도 모수와 상관 관계가 있다.가능성은 여러 개의 국부적 최대치를 가질 수 있으며, 따라서 자유도를 상당히 낮은 값으로 고정하고 이것을 주어진 것으로 간주하는 다른 매개변수를 추정해야 하는 경우가 많다.일부 저자들은^{[citation needed]} 3에서 9 사이의 가치가 종종 좋은 선택이라고 보고한다.Venables와 Ripley는^{[citation needed]} 5의 값이 종종 좋은 선택이라고 제안한다.

학생의 t-과정

실질적인 회귀 분석과 예측 요구를 위해 학생의 t-프로세스가 도입되었는데, 이는 기능에 대한 학생 t-분산의 일반화다.학생의 t-프로세스는 가우스 분포로 구성되는 것처럼 학생의 t-분포에서 구성된다.가우스 공정의 경우 모든 값 집합은 다차원 가우스 분포를 가진다.Analogiusly, ${\displaystyle X(t)}$ is a Student t-process on an interval ${\displaystyle I=[a,b]}$ if the correspondent values of the process ${\displaystyle X(t_{1}),...,X(t_{n})}$ (${\displaystyle t_{i}\in I}$) have a joint multivariate Student t-di공로를 ^[29]세우다이러한 프로세스는 회귀 분석, 예측, 베이시안 최적화 및 관련 문제에 사용된다.다변량 회귀 분석 및 다중 출력 예측의 경우 다변량 학생 t-프로세스를 도입하여 사용한다.^[30]

선택한 값 표

다음 표에는 일방 또는 양면 임계 영역의 범위에 대해 자유도가 ν인 t-분산 값이 나열되어 있다.첫 번째 열은 ν이고, 상단을 따라 있는 백분율은 신뢰수준이며, 표의 본문에 있는 숫자는 신뢰구간에 관한 절에 기술된 $t{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$,${\displaystyle n_{}}$ - ${\displaystyle 1_{}}$ ${\$ 요인이다$$.

무한 ν의 마지막 행은 자유도가 무한히 많은 t 분포가 정규 분포이기 때문에 정규 분포에 임계 포인트를 준다는 점에 유의한다.(위의 관련 분포를 참조하십시오.)

일방적	75%	80%	85%	90%	95%	97.5%	99%	99.5%	99.75%	99.9%	99.95%
양면	50%	60%	70%	80%	90%	95%	98%	99%	99.5%	99.8%	99.9%
1	1.000	1.376	1.963	3.078	6.314	12.71	31.82	63.66	127.3	318.3	636.6
2	0.816	1.080	1.386	1.886	2.920	4.303	6.965	9.925	14.09	22.33	31.60
3	0.765	0.978	1.250	1.638	2.353	3.182	4.541	5.841	7.453	10.21	12.92
4	0.741	0.941	1.190	1.533	2.132	2.776	3.747	4.604	5.598	7.173	8.610
5	0.727	0.920	1.156	1.476	2.015	2.571	3.365	4.032	4.773	5.893	6.869
6	0.718	0.906	1.134	1.440	1.943	2.447	3.143	3.707	4.317	5.208	5.959
7	0.711	0.896	1.119	1.415	1.895	2.365	2.998	3.499	4.029	4.785	5.408
8	0.706	0.889	1.108	1.397	1.860	2.306	2.896	3.355	3.833	4.501	5.041
9	0.703	0.883	1.100	1.383	1.833	2.262	2.821	3.250	3.690	4.297	4.781
10	0.700	0.879	1.093	1.372	1.812	2.228	2.764	3.169	3.581	4.144	4.587
11	0.697	0.876	1.088	1.363	1.796	2.201	2.718	3.106	3.497	4.025	4.437
12	0.695	0.873	1.083	1.356	1.782	2.179	2.681	3.055	3.428	3.930	4.318
13	0.694	0.870	1.079	1.350	1.771	2.160	2.650	3.012	3.372	3.852	4.221
14	0.692	0.868	1.076	1.345	1.761	2.145	2.624	2.977	3.326	3.787	4.140
15	0.691	0.866	1.074	1.341	1.753	2.131	2.602	2.947	3.286	3.733	4.073
16	0.690	0.865	1.071	1.337	1.746	2.120	2.583	2.921	3.252	3.686	4.015
17	0.689	0.863	1.069	1.333	1.740	2.110	2.567	2.898	3.222	3.646	3.965
18	0.688	0.862	1.067	1.330	1.734	2.101	2.552	2.878	3.197	3.610	3.922
19	0.688	0.861	1.066	1.328	1.729	2.093	2.539	2.861	3.174	3.579	3.883
20	0.687	0.860	1.064	1.325	1.725	2.086	2.528	2.845	3.153	3.552	3.850
21	0.686	0.859	1.063	1.323	1.721	2.080	2.518	2.831	3.135	3.527	3.819
22	0.686	0.858	1.061	1.321	1.717	2.074	2.508	2.819	3.119	3.505	3.792
23	0.685	0.858	1.060	1.319	1.714	2.069	2.500	2.807	3.104	3.485	3.767
24	0.685	0.857	1.059	1.318	1.711	2.064	2.492	2.797	3.091	3.467	3.745
25	0.684	0.856	1.058	1.316	1.708	2.060	2.485	2.787	3.078	3.450	3.725
26	0.684	0.856	1.058	1.315	1.706	2.056	2.479	2.779	3.067	3.435	3.707
27	0.684	0.855	1.057	1.314	1.703	2.052	2.473	2.771	3.057	3.421	3.690
28	0.683	0.855	1.056	1.313	1.701	2.048	2.467	2.763	3.047	3.408	3.674
29	0.683	0.854	1.055	1.311	1.699	2.045	2.462	2.756	3.038	3.396	3.659
30	0.683	0.854	1.055	1.310	1.697	2.042	2.457	2.750	3.030	3.385	3.646
40	0.681	0.851	1.050	1.303	1.684	2.021	2.423	2.704	2.971	3.307	3.551
50	0.679	0.849	1.047	1.299	1.676	2.009	2.403	2.678	2.937	3.261	3.496
60	0.679	0.848	1.045	1.296	1.671	2.000	2.390	2.660	2.915	3.232	3.460
80	0.678	0.846	1.043	1.292	1.664	1.990	2.374	2.639	2.887	3.195	3.416
100	0.677	0.845	1.042	1.290	1.660	1.984	2.364	2.626	2.871	3.174	3.390
120	0.677	0.845	1.041	1.289	1.658	1.980	2.358	2.617	2.860	3.160	3.373
∞	0.674	0.842	1.036	1.282	1.645	1.960	2.326	2.576	2.807	3.090	3.291
일방적	75%	80%	85%	90%	95%	97.5%	99%	99.5%	99.75%	99.9%	99.95%
양면	50%	60%	70%	80%	90%	95%	98%	99%	99.5%	99.8%	99.9%

신뢰 구간 계산

크기가 11이고 표본 평균이 10이고 표본 분산 2인 표본이 있다고 가정합시다.자유도가 10인 90%인 경우 표의 단측 t-값은 1.372이다.그런 다음 다음 다음에서 계산된 신뢰 구간을 사용하여

${\displaystyle {\x}_{n}\pm t_{\alpha,\nu}{\frac {S_{n}}{\sqrt{n}}}},$

우리는 90%의 자신감으로 아래에 진정한 평균이 있다고 판단한다.

${\displaystyle 10+1.372{\frac {\sqrt{2}}{\\sqrt{11}}=10.585.}$

즉, 특정 표본으로부터 이 방법에 의해 상한 임계값을 계산하는 시간의 90%는 이 상한 임계값이 참 평균을 초과한다.

그리고 90%의 자신감으로 우리는 위에 있는 진정한 평균을 가지고 있다.

${\displaystyle 10-1.372{\frac {\sqrt{2}}{\\sqrt{11}}=9.414.}$

즉, 특정 표본으로부터 이 방법에 의해 낮은 임계값을 계산하는 시간의 90%가, 이 낮은 임계값은 참 평균보다 낮다.

따라서 80% 신뢰도(100% - 2×(1 - 90%) = 80%로 계산됨)에서 구간 내에 실제 평균이 거짓말을 함

${\displaystyle \left(10-1.372{\frac{\sqrt{2}}:\sqrt{11}}},10+1.372{\sqrt{2}}:{\sqrt{11}}\right)=(9.414,10.585).}$

상한과 하한 임계값이 주어진 표본에서 이 방법에 의해 계산되는 시간의 80%를 말한다면, 참 평균은 상한 임계값보다 낮으며 하한 임계값보다 높다고 말하는 것은 실제 평균이 계산된 특정 상한과 하한 임계값 사이에 있을 확률이 80%라고 말하는 것과 같지 않다.이 방법에 따라; 신뢰구간과 검사의 오류를 보라.

오늘날, R 프로그래밍 언어와 같은 통계 소프트웨어와 많은 스프레드시트 프로그램에서 이용할 수 있는 기능들은 표 없이 t-분포와 그것의 역분포의 값을 계산한다.

참고 항목

메모들

참조

• Senn, S.; Richardson, W. (1994). "The first t-test". Statistics in Medicine. 13 (8): 785–803. doi:10.1002/sim.4780130802. PMID 8047737.
• Hogg RV, Craig AT (1978). Introduction to Mathematical Statistics (4th ed.). New York: Macmillan. ASIN B010WFO0SA.
• Venables, W. N.; Ripley, B. D. (2002). Modern Applied Statistics with S (Fourth ed.). Springer.
• Gelman, Andrew; John B. Carlin; Hal S. Stern; Donald B. Rubin (2003). Bayesian Data Analysis (Second ed.). CRC/Chapman & Hall. ISBN 1-58488-388-X.

외부 링크

• "Student distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 수학의 일부 단어의 초기 알려진 사용법 (S) (학생 분포라는 용어의 역사에 대한 설명)
• Rouaud, M. (2013), Probability, Statistics and Estimation (PDF) (short ed.) 112페이지의 첫 번째 학생.
• 학생 t-Distribution,^{[dead link]} ck12