관리도

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정확한 인용문을 도입하여 이 기사의 개선에 도움을 주시기 바랍니다. (2013년 12월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

관리도
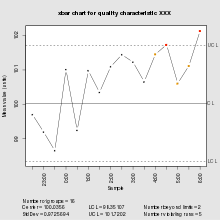품질의 7가지 기본 도구 중 하나
최초 설명자	월터 A.슈하트
목적	품질 관련 문제에 대한 공정의 정식 검사 여부 결정

관리도(Shewhart 차트라고도 함) Shewhart) 또는 공정 행동 차트는 제조 또는 비즈니스 공정이 관리 상태에 있는지 여부를 판단하는 데 사용되는 통계 공정 관리 도구입니다.관리도는 SPM(Statistical Process Monitoring)을 위한 그래픽 장치라고 하는 것이 적절합니다.기존 관리도는 공정 분포의 기본 형태가 알려진 경우 공정 모수를 모니터링하도록 설계되어 있습니다.그러나 21세기에는 기본 프로세스 분포에 대한 지식이 없어도 착신 데이터 스트리밍을 모니터링할 수 있는 보다 고급 기술이 제공되고 있습니다.무배포 관리도가 점점 인기를 끌고 있다.

개요

관리도를 분석한 결과 공정이 현재 관리 상태에 있음을 알 수 있는 경우(즉, 공정에 공통적인 출처에서만 변동이 발생하며 안정적임) 공정 관리 모수를 수정하거나 변경할 필요가 없습니다.또한 프로세스의 데이터를 사용하여 프로세스의 미래 성능을 예측할 수 있습니다.관리도에 모니터링되는 공정이 관리 상태에 있지 않음을 나타내는 경우 관리도를 분석하면 공정 ^[1]성능이 저하되므로 변동 원인을 파악하는 데 도움이 됩니다.안정적이지만 바람직한 (사양) 한계를 벗어나 작동하는 공정(예: 스크랩 속도는 통계적 통제 상태에 있을 수 있지만 바람직한 한계를 초과함)은 현재 성능의 원인을 이해하고 ^[2]프로세스를 근본적으로 개선하기 위한 신중한 노력을 통해 개선되어야 한다.

관리도는 품질 ^[3]관리를 위한 7가지 기본 도구 중 하나입니다.일반적으로 연속형 데이터 또는 변수 데이터라고도 하는 시계열 데이터에 관리도가 사용됩니다.논리적 비교 가능성이 있는 데이터(즉, 동시에 모두 채취한 표본이나 다른 개인의 성능을 비교하려는 경우)에도 사용할 수 있지만,^[4] 이 작업에 사용되는 차트 유형은 고려해야 합니다.

역사

관리도는 월터 A에 의해 발명되었다. 1920년대에 ^[5]벨 연구소에서 일했던 쉬와트입니다그 회사의 엔지니어들은 전화 전송 시스템의 신뢰성을 개선하기 위해 노력해왔다.앰프 등 장비를 지하에 파묻어야 했기 때문에 고장 빈도와 수리 빈도를 줄여야 할 필요성이 커졌다.1920년까지 엔지니어들은 이미 제조 공정의 변화를 줄이는 것의 중요성을 깨달았습니다.또한 부적합에 대한 지속적인 프로세스 조정이 실제로 변동과 품질 저하를 증가시킨다는 것을 깨달았습니다.Shewhart는 공통 및 특수 변동 원인의 관점에서 문제를 정리했고 1924년 5월 16일 두 가지를 구별하기 위한 도구로서 관리도를 소개하는 내부 메모를 작성했다.쉐하트의 상사 조지 에드워즈는 "닥터 쉐하트는 약 한 페이지 정도의 짧은 메모를 준비했다.그 페이지의 약 3분의 1이 간단한 도표로 넘어갔는데, 오늘날에는 도식적인 관리도로 인식될 것입니다.이 도표와 그 앞뒤에 있는 짧은 텍스트는 오늘날 우리가 프로세스 ^[6]품질 관리라고 알고 있는 것과 관련된 모든 기본 원칙과 고려 사항을 명시하고 있습니다."Shewhart는 생산 공정을 통계적 통제 상태로 전환하고, 공통 원인에 의한 변동만 존재하는 상태로 유지하고, 향후 생산량을 예측하고 공정을 경제적으로 관리하기 위해 필요하다고 강조했다.

Shewhart는 신중하게 설계된 실험을 통해 관리도와 통계 관리 상태의 개념을 위한 기초를 만들었다.Shewhart는 순수 수학 통계 이론에서 도출한 반면, 물리적 과정의 데이터는 일반적으로 "정규 분포 곡선"(일반적으로 "벨 곡선"이라고도 함)을 생성한다는 것을 이해했다.그는 관측된 제조 데이터의 변동이 자연 상태의 데이터와 항상 같은 방식으로 동작하지는 않는다는 것을 발견했습니다(브라운 입자의 움직임).Shewhart는 모든 공정에서 변동을 표시하는 반면, 일부 공정은 공정의 자연스러운 통제된 변동을 표시하는 반면 다른 공정은 공정 인과 체계에 ^[7]항상 존재하지 않는 통제되지 않은 변동을 보인다고 결론을 내렸습니다.

1924년 또는 1925년, Shewhart의 혁신은 당시 Hawthorne 시설에서 일하던 W. Edwards Deming의 눈에 띄었다.데밍은 후에 미국 농무부에서 일했고 미국 인구조사국의 수학 고문이 되었다.이후 반세기 동안, 데밍은 슈하트의 업적 중 가장 뛰어난 챔피언이자 지지자가 되었다.제2차 세계대전 말기에 일본이 패전한 후, 데밍은 연합군 최고사령관의 통계 고문으로 일했다.이후 일본 생활에의 관여와 오랜 산업 컨설턴트로서의 경력은 1950년대와 1960년대에 걸쳐 일본 제조업계에 Shewhart의 사고와 관리도를 널리 보급시켰다.

차트 상세

관리도는 다음과 같이 구성됩니다.

• 공정에서 서로 다른 시간(예: 데이터)에 추출된 표본의 품질 특성에 대한 측정값의 통계량(예: 평균, 범위, 비율)을 나타내는 점
• 모든 표본을 사용하여 이 통계량의 평균을 계산하거나(예: 평균의 평균, 범위의 평균, 비율의 평균) 변화를 평가할 수 있는 기준 기간에 대해 계산한다.마찬가지로 중위수를 대신 사용할 수 있습니다.
• 중심선은 통계량의 평균 또는 중위수 값에 그려집니다.
• 통계량의 표준 편차(예: 평균의 sqrt(분산))는 모든 표본을 사용하여 계산되거나 변화를 평가할 수 있는 기준 기간에 대해 다시 계산됩니다.XmR 관리도의 경우 표준 편차의 근사치이며, 는^{[clarification needed]} 표준 편차가 발생하는 시간 경과에 따른 공정의 균질성을 가정하지 않습니다.
• 공정 출력이 통계적으로 '달리'로 간주되고 일반적으로 중심선에서 3 표준 편차로 그려지는 임계값을 나타내는 관리 상한 및 하한("자연 공정 한계"라고도 함)

차트에는 다음과 같은 기타 옵션 기능이 있습니다.

• 더 제한적인 상한 및 하한 경고 또는 관리 한계선으로, 별도의 선으로 그려지며, 일반적으로 중심선 위와 아래에 두 개의 표준 편차가 표시됩니다.공정에서 변동성을 더 엄격하게 제어해야 할 때 정기적으로 사용됩니다.
• 각 구역의 관측 빈도를 관리하는 규칙을 추가하여 구역으로 나눈다.
• 프로세스의 품질을 담당하는 품질 엔지니어가 결정하는 관심 이벤트가 포함된 주석
• 특수 원인에 대한 조치

(n.b. 신호 검출에는 몇 가지 규칙 집합이 있습니다.이것은 1개의 집합일 뿐입니다.규칙 집합은 명확하게 기술해야 합니다.)

1. 관리 한계를 벗어난 모든 점
2. 중앙선 위 또는 아래 모두 7포인트 실행 - 생산을 중지합니다.
   • 검역 및 100% 확인
   • 프로세스를 조정합니다.
   • 5개의 연속 표본 확인
   • 프로세스를 속행합니다.
3. 7포인트 업 또는 다운 실행 - 위와 같은 절차

차트 사용 현황

공정이 관리 상태에 있고 공정 통계량이 정규 분포인 경우 모든 점의 99.7300%가 관리 한계 사이에 들어갑니다.한계를 벗어난 관측치 또는 내부의 체계적인 패턴은 특수 원인 변동으로 알려진 새로운(예상하지 않은) 변동원의 도입을 시사합니다.변동 증가는 품질 비용의 증가를 의미하므로, 관리도는 특수 원인의 존재를 "신호화"하기 위해 즉각적인 조사가 필요합니다.

따라서 제어 한계는 매우 중요한 의사결정 보조 수단이 됩니다.관리 한계는 공정 동작에 대한 정보를 제공하며 규격 목표값이나 공차와는 아무런 관련이 없습니다.실제로 공정 설계는 단순히 원하는 수준에서 공정 특성을 전달할 수 없기 때문에 공정 평균(따라서 중심선)이 품질 특성의 지정된 값(또는 목표값)과 일치하지 않을 수 있습니다.

공정과 관련된 사람들(예: 기계 조작자)이 사양에 따라 수행하는 데 초점을 맞추는 경향 때문에 관리도는 규격 한계 또는 목표값을 제한합니다. 실제로 가장 비용이 적게 드는 작업 과정은 공정 변동을 가능한 낮게 유지하는 것입니다.목표 사양과 동일한 자연 중심이 아닌 공정을 목표 사양에 맞게 수행하려고 하면 공정의 변동성이 증가하고 비용이 크게 증가하며 운영의 비효율성이 크게 발생합니다.그러나 공정 능력 연구에서는 자연 공정 한계(관리 한계)와 규격 사이의 관계를 조사합니다.

관리도의 목적은 공정 변동성의 증가를 나타내는 사건을 단순하게 탐지하는 것입니다.^[8] 공정 특성이 지속적으로 변화하는 경우에는 이 간단한 결정이 어려울 수 있습니다. 관리도는 통계적으로 객관적인 변경 기준을 제공합니다.변화가 검출되어 양호하다고 판단되면 그 원인을 특정하여 새로운 작업방식이 될 수 있습니다.변화가 나쁘면 그 원인을 특정하여 제거해야 합니다.

경고 한도를 추가하거나 관리도를 구역별로 세분화하는 목적은 잘못된 사항이 있을 경우 조기 통보하는 것이다.품질 엔지니어는 특수 원인이 존재하는지 여부를 판단하기 위해 즉시 프로세스 개선 작업을 시작하는 대신 프로세스가 진정으로 관리 상태에 있음을 분명히 할 때까지 프로세스 출력에서 샘플을 추출하는 속도를 일시적으로 높일 수 있습니다.3 시그마 제한에서는 공통 원인에 따라 왜곡된 프로세스의 경우 22포인트마다 1포인트 미만, 정규 분포 ^[9]프로세스의 경우 약 370포인트(1/370.4)마다 1포인트 미만의 신호가 발생한다는 점에 주의해 주십시오.2-시그마 경고 수준은 정규 분포 데이터의 22개(1/21.98) 표시된 점에 대해 약 한 번 도달한다. (예를 들어 분산이 존재하는 실질적으로 모든 기본 분포에서 추출한 충분히 큰 표본의 평균은 중앙 한계 정리에 따라 정규 분포에 따라 정규 분포된다.)

제한의 선택

Shewhart는 다음과 같은 기준으로 3-시그마(3-표준 편차) 한계를 설정합니다.

• 확률 분포에서 평균으로부터 k 표준 편차보다 큰 결과가 나올 확률은 최대 1/k라는² 체비셰프의 부등식의 대략적인 결과입니다.
• Vysochanskii의 더 좋은 결과-페투닌 부등식, 단일한 확률 분포의 경우 평균에서 k 표준 편차보다 큰 결과가 나올 확률은 최대 4/(9k²)입니다.
• 매우 일반적인 확률 분포인 정규 분포에서는 관측치의 99.7%가 평균의 세 표준 편차 내에서 발생합니다(정규 분포 참조).

Shewhart는 다음과 같이 결론을 요약했다.

...우리가 우연히 사용하는 기준이 고급 통계 이론에서 훌륭한 조상을 가지고 있다는 사실은 그것을 사용하는 것을 정당화하지 않는다.그러한 정당성은 그것이 효과가 있다는 경험적 증거로부터 나와야 한다.실제 엔지니어가 말하듯 푸딩의 증거는 먹어봐야 합니다.^[10]

Shewhart는 처음에 확률 분포에 기초한 한계를 실험했지만 결국 다음과 같이 썼다.

통계적 통제 상태를 특성화하려는 초기 시도 중 일부는 주파수 함수 f의 특별한 형태가 존재한다는 믿음에서 영감을 얻었으며, 일반 법칙이 그러한 상태를 특성화한다고 초기에 주장되었다. 일반 법칙이 불충분한 것으로 판명되면, 일반화된 함수 형태를 시도했다. 그러나 오늘날, 독특한 기능적 형태 f를 찾는 모든 희망은 ^[11]산산조각이 났다.

관리도는 휴리스틱으로 사용됩니다.Deming은 이것이 가설 테스트가 아니며 Neyman-Pearson 보조정리에 의해 동기 부여되지 않았다고 주장했다.그는 대부분의 산업적 상황에서 모집단과 표본추출범위의 분리된 특성으로 인해 전통적인 통계기법의 사용이 훼손되었다고 주장했다.Deming의 의도는 프로세스의 원인 시스템에 대한 통찰력을 찾는 것이었습니다... 광범위한 알 수 없는 상황, 미래 및 과거...^{[citation needed]}그는 이런 상황에서 3 시그마 한계는 경제적 손실을 최소화하는 합리적이고 경제적인 지침을 제공한다고 주장했다.다음 두 가지 ^{[citation needed]}오류로부터.

1. 실제로 원인이 시스템(공통 원인)에 속하는 경우에는 변동 또는 오류를 특수 원인(지정 가능한 원인)으로 돌립니다.(타입 I 오류 또는 False Positive라고도 함)
2. 실제로 원인이 특수 원인(지정 가능한 원인)인 경우 시스템(공통 원인)의 변화 또는 오류를 원인으로 돌립니다.(타입 II 오류 또는 False Negative라고도 함)

표준편차의 산출

관리 한계 계산의 경우 공정의 공통 원인 변동에 대한 표준 편차(오차)가 필요합니다.따라서 표본 분산의 관점에서 일반적인 추정치는 변동의 공통 원인 및 특수 원인 모두에서 총 제곱 오차 손실을 추정하기 때문에 사용되지 않는다.

다른 방법은 표본의 범위와 Leonard H. C.에 의해 도출된 표준 편차 사이의 관계를 사용하는 것입니다. Tippett은 ^{[citation needed]}특수 원인을 나타내는 극단적 관측치의 영향을 덜 받는 경향이 있는 추정치입니다.

신호 검출 규칙

가장 일반적인 세트는 다음과 같습니다.

• 웨스턴 일렉트릭의 법칙
• Wheeler 규칙(Western Electric Zone^[12] 테스트에 상당)
• 넬슨의 법칙

6, 7, 8, 9가 모두 다양한 작가들에 의해 주창되고 있는 가운데, 모두 중심선의 같은 쪽에 있는 일련의 관찰이 신호로 간주되어야 하는 시간에 대해 특별한 논란이 있었다.

규칙 집합을 선택하는 데 가장 중요한 원칙은 데이터를 검사하기 전에 선택하는 것입니다.데이터를 확인한 후 규칙을 선택하면 데이터에 의해 제시된 검정 효과 때문에 유형 I 오류율이 증가하는 경향이 있습니다.

대체 베이스

1935년 영국표준협회는 Egon Pearson의 영향과 Shewhart의 정신에 반하여 관리도를 채택하여 3-시그마 한계를 정규 분포의 백분위수에 기초한 한계로 대체하였다.이 움직임은 존 오클랜드와 다른 사람들에 의해 계속 대표되고 있지만, 쉐하트-데밍 전통에 있는 작가들에 의해 널리 비난 받아왔다.

관리도 성능

점이 특정 관리도에 대해 설정된 한계를 벗어나면 기본 공정에 대한 책임자는 특수 원인이 발생했는지 여부를 확인할 것으로 예상됩니다.그렇다면 특수 원인에 의한 결과가 일반적인 원인에 의한 결과보다 좋은지 나쁜지 판단하는 것이 적절합니다.만약 더 나쁘다면, 그 원인은 가능하면 제거되어야 한다.더 나은 경우에는 ^{[citation needed]}결과를 생성하는 시스템 내에 특수 원인을 의도적으로 유지하는 것이 적절할 수 있습니다.

공정이 관리 상태에 있는 경우에도(즉, 시스템에 특수 원인이 존재하지 않는 경우) 점이 3-시그마 관리 한계를 초과할 확률은 약 0.27%입니다.따라서 적절하게 구성된 관리도에 표시된 관리 프로세스에서도 실제로는 발생하지 않았더라도 결국 특수 원인이 존재할 수 있다는 신호가 됩니다.3-시그마 한계를 사용하는 Shewhart 관리도의 경우 이 잘못된 경보가 1/0.0027 또는 370.4 관측치마다 평균 한 번씩 발생합니다.따라서 Shewhart 관리도의 관리 평균 런 길이(또는 관리 ARL)는 370.^{[citation needed]}4입니다.

한편, 특별한 원인이 발생할 경우 차트에 즉각적인 경보 조건이 생성될 정도로 크지 않을 수 있다.특수 원인이 발생하면 해당 공정의 평균 및/또는 분산의 변화를 측정하여 해당 원인을 설명할 수 있습니다.이러한 변화를 수량화하면 ^{[citation needed]}관리도에 대한 관리 이탈 ARL을 확인할 수 있습니다.

Shewhart 관리도는 관리 이탈 상태의 ARL이 매우 짧기 때문에 공정 평균 또는 분산의 큰 변화를 탐지하는 데 매우 뛰어난 것으로 나타났습니다.그러나 작은 변화(예: 평균의 1-시그마 또는 2-시그마 변화)의 경우 Shewhart 관리도는 이러한 변화를 효율적으로 탐지하지 못합니다.EWMA 관리도, CUSUM 관리도 및 실시간 대비 차트 등 최신 데이터 ^[13]지점 이전에 수집된 관측치의 정보를 사용하여 보다 효율적으로 작은 변화를 탐지하는 다른 유형의 관리도도 개발되었습니다.

많은 관리도는 가우스 가정이 있는 숫자 데이터에 가장 적합합니다.실시간 대비 차트는 복잡한 특성(예: 고차원, 숫자 및 범주형 혼합, 결측값, 비가우스, 비선형 관계)^[13]을 가진 프로세스를 모니터링하기 위해 제안되었다.

비판

몇몇 저자들은 관리도가 우도 ^{[citation needed]}원칙에 위배된다는 이유로 이를 비판하였다.그러나 이 원칙 자체는 논란의 여지가 있으며, 관리도를 지지하는 사람들은 일반적으로 통계적 관리 상태에 있지 않은 공정에 대해 우도 함수를 지정하는 것은 불가능하며, 특히 공정의 원인 체계에 대한 지식이 ^{[citation needed]}약하다고 주장한다.

일부 저자는 평균이 일반적으로 변동성과 난이도가 ^{[citation needed]}높은 기하학적 분포를 따르기 때문에 관리도 성능 비교에 평균 런 길이(ARL)를 사용하는 것을 비판하였다.

일부 저자는 대부분의 관리도가 숫자 데이터에 초점을 맞춘다고 비판했습니다.오늘날 프로세스 데이터는 훨씬 더 복잡할 수 있습니다(예: 비가우스어, 숫자 및 범주형 혼합, 결측값).^[13]

차트의 종류

차트	공정 관찰	공정 관측치 관계	공정 관측치 유형	탐지할 이동 크기
${\displaystyle \stackrel{}{x}}$ $（$ \ $displaystyle$\ $bar${ $x$} ）및$$ R 관리도	한 부분군 내의 품질 특성 측정	독립적인	변수	라지( 11.5 †)
$(\$ 및$$ s 차트	한 부분군 내의 품질 특성 측정	독립적인	변수	라지( 11.5 †)
Shewhart 개별 관리도(ImR 관리도 또는 XmR 관리도)	한 관측치에 대한 품질 특성 측정	독립적인	변수†	라지( 11.5 †)
삼원 차트	한 부분군 내의 품질 특성 측정	독립적인	변수	라지( 11.5 †)
p차트	한 부분군 내에서 부적합한 부분군	독립적인	속성†	라지( 11.5 †)
np-차트	한 부분군 내 번호 부적합	독립적인	속성†	라지( 11.5 †)
c차트	한 부분군 내 불량품의 수	독립적인	속성†	라지( 11.5 †)
u차트	한 부분군 내의 단위당 부적합	독립적인	속성†	라지( 11.5 †)
EWMA 관리도	한 부분군 내 품질 특성 측정의 지수 가중 이동 평균	독립적인	속성 또는 변수	소형 (1.5 °C 미만)
누적합[CUSUM] 관리도	한 부분군 내 품질 특성 측정값의 누적 합계	독립적인	속성 또는 변수	소형 (1.5 °C 미만)
시계열 모형	한 부분군 내의 품질 특성 측정	자기 상관	속성 또는 변수	없음
회귀 관리도	한 부분군 내의 품질 특성 측정	공정 관리 변수에 종속됨	변수	라지( 11.5 †)

^†일부 실무자는 계수형 데이터에 대해 개별 관리도를 사용할 것을 권장합니다. 특히 이원 분포 데이터(p- 및 np-차트) 또는 포아송 분포 데이터(u- 및 c-차트)의 가정이 ^[14]위반되는 경우에는 더욱 그렇습니다.이 관행에 대한 두 가지 주요 이유가 제시된다.첫째, 통계적 관리에는 정규성이 필요하지 않으므로 개체 관리도를 비정규 ^[15]데이터와 함께 사용할 수 있습니다.둘째, 계수형 관리도는 (확률 분포를 가정하여) 평균 비율에서 직접 분산 측도를 도출하는 반면, 개별 관리도는 평균과 무관하게 데이터에서 분산 측도를 도출하여 개별 관리도를 분포에 대한 가정의 위반에 대한 계수형 관리도보다 더 견고하게 만듭니다.전체 인구 ^[16]중 가장 많죠.이항 분포와 포아송 분포가 정규 분포에 가까운 경우, 즉 p- 및 np-차트의 경우 시행 횟수가 1000회 이상 또는 u- 및 c-차트의 경우 500회 이상일 때 개체 관리도의 대체가 큰 카운트에 가장 잘 작동한다는 것을 알 수 있습니다.

이 방법을 비판하는 사람들은 공정 데이터가 정규 분포를 따르지 않거나 이원 분포(또는 포아송)되지 않은 경우와 같이 기본 가정이 위반되는 경우에는 관리도를 사용해서는 안 된다고 주장합니다.이러한 프로세스는 관리 상태에 있지 않으므로 관리도를 적용하기 전에 개선해야 합니다.또한 이러한 편차가 존재하는 상태에서 관리도를 적용하면 관리도의 유형 I 및 유형 II 오류율이 증가하므로 관리도는 거의 ^{[citation needed]}실용적이지 않을 수 있습니다.

「 」를 참조해 주세요.

• 분석 및 열거 통계 연구
• 공통 원인 및 특수 원인
• 무배포 관리도
• W. 에드워즈 데밍
• 프로세스 능력
• 품질의 7가지 기본 도구
• 식스 시그마
• 통계 프로세스 제어
• 종합 품질 관리

레퍼런스

참고 문헌

• Deming, W. E. (1975). "On probability as a basis for action". The American Statistician. 29 (4): 146–152. CiteSeerX 10.1.1.470.9636. doi:10.2307/2683482. JSTOR 2683482.
• Deming, W. E. (1982). Out of the Crisis: Quality, Productivity and Competitive Position. ISBN 978-0-521-30553-2.
• Deng, H.; Runger, G.; Tuv, Eugene (2012). "System monitoring with real-time contrasts". Journal of Quality Technology. 44 (1): 9–27. doi:10.1080/00224065.2012.11917878. S2CID 119835984.
• Mandel, B. J. (1969). "The Regression Control Chart". Journal of Quality Technology. 1 (1): 1–9. doi:10.1080/00224065.1969.11980341.
• Oakland, J. (2002). Statistical Process Control. ISBN 978-0-7506-5766-2.
• Shewhart, W. A. (1931). Economic Control of Quality of Manufactured Product. ISBN 978-0-87389-076-2.
• Shewhart, W. A. (1939). Statistical Method from the Viewpoint of Quality Control. ISBN 978-0-486-65232-0.
• Wheeler, D. J. (2000). Normality and the Process-Behaviour Chart. ISBN 978-0-945320-56-2.
• Wheeler, D. J.; Chambers, D. S. (1992). Understanding Statistical Process Control. ISBN 978-0-945320-13-5.
• Wheeler, Donald J. (1999). Understanding Variation: The Key to Managing Chaos (2nd ed.). SPC Press. ISBN 978-0-945320-53-1.

외부 링크

• NIST/SEMATECH 통계 방법 전자 핸드북
• 관리도를 사용한 감시 및 제어