삼각 타일링 벌집
Triangular tiling honeycomb| 삼각 타일링 벌집 | |
|---|---|
 | |
| 유형 | 쌍곡선 정규 벌집 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | {3,6,3} h{6,3,6} h{6,3[3]}파운드 {3[3,3]} |
| 콕시터-딘킨 도표 | |
| 세포 | {3,6} |
| 얼굴 | 삼각형 {3} |
| 에지 피겨 | 삼각형 {3} |
| 정점수 | 육각 타일링 |
| 이중 | 셀프듀얼 |
| 콕시터 그룹 | [3,6,3] } [6,3[3]] 3 [3[3,3]] |
| 특성. | 정규 |
삼각형 타일링 허니콤은 쌍곡선 3공간에 있는 11개의 파라콤팩트 공간 채우기 테셀레이션(또는 허니컴) 중 하나이다.무한 세포와 꼭지점 형상을 가지고 있고, 모든 정점이 무한에서 이상적인 점으로 되어 있기 때문에 파라콤팩트라고 불린다.슐래플리 기호 {3,6,3}이(가) 삼각 타일링 셀로 구성되어 있다.벌집모양의 각 가장자리는 세 개의 세포로 둘러싸여 있으며, 각각의 꼭지점은 그곳에서 무한히 많은 세포가 만나는 이상적인 것이다.그것의 꼭지점은 육각형 타일링이다.
기하학적 벌집이란 다면체나 고차원적 세포의 공간을 채워서 틈이 생기지 않도록 하는 것이다.그것은 어떤 차원에서도 보다 일반적인 수학적 타일링 또는 테셀레이션의 예다.
허니컴은 보통 볼록한 균일한 허니컴과 같은 일반적인 유클리드("평평평한") 공간에서 만들어진다.그것들은 쌍곡선 균일 벌집과 같은 비유클리드 공간에도 건설될 수 있다.어떤 유한 균일 폴리토프는 구면 공간에 균일한 벌집을 형성하기 위해 그것의 원주에 투영될 수 있다.
대칭
그것은 2개의 낮은 반사 대칭 구조를 가지고 있는데, 이는 교대로 6각형 타일링 벌집, £ 및 에서 3종류의 삼각형 기울기를 모든 가장자리를 중심으로 번갈아 가며 한다.Coxeter 표기법에서 3번째 미러와 4번째 미러를 제거하면 [3,6[3,3],3*]이(가) 새로운 Coxeter 그룹[3], , 부분군 색인 6을 생성한다.기본영역은 6배 더 크다.Coxeter 다이어그램에 따르면 새로운 기본 영역에 있는 최초의 원본 거울의 복사본 3개가 있다: £.
관련 틸링
그것은 2D 쌍곡선 무한궤도 타일링과 유사하며, 무한궤도 면과 이상적인 표면에 모든 정점을 가지고 있다.
관련 허니컴
삼각형 타일링 허니콤은 3칸의 일반 쌍곡 벌집이며, 11개의 파라콤팩트 벌집 중 하나이다.
| 11개의 파라콤팩트 일반 꿀벌집 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 {6,3,3} |  {6,3,4} |  {6,3,5} |  {6,3,6} |  {4,4,3} |  {4,4,4} | ||||||
 {3,3,6} |  {4,3,6} |  {5,3,6} |  {3,6,3} |  {3,4,4} | |||||||
[3,6,3] Coxeter 그룹 계열에는 9개의 균일한 벌집이 있는데, 여기에는 이 정규 형태와 비트롤링 형태 t1,2{3,6,3}가 포함되며, 모든 잘린 육각형 타일링 면이 있다.
| {3,6,3} | r{3,6,3} | t{3,6,3} | rr{3,6,3} | t0,3{3,6,3} | 2t{3,6,3} | tr{3,6,3} | t0,1,3{3,6,3} | t0,1,2,3{3,6,3} |
|---|---|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |  |  |
허니콤은 삼각형 테두리를 가진 일련의 폴리초라와 허니콤의 일부분이기도 하다.
| {3,p,3}개의 폴리토페스 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 공간 | S3 | H3 | |||||||||
| 형태 | 유한한 | 작은 | 파라콤팩트 | 비컴팩트 | |||||||
| {3,p,3} | {3,3,3} | {3,4,3} | {3,5,3} | {3,6,3} | {3,7,3} | {3,8,3} | ... {3,∞,3} | ||||
| 이미지 |  |  |  |  |  |  |  | ||||
| 세포 |  {3,3} |  {3,4} |  {3,5} |  {3,6} |  {3,7} |  {3,8} |  {3,∞} | ||||
| 꼭지점 형상을 나타내다 |  {3,3} |  {4,3} |  {5,3} |  {6,3} |  {7,3} |  {8,3} |  {∞,3} | ||||
수정삼각형 타일링 벌집
| 수정삼각형 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | r{3,6,3} h2{6,3,6} |
| 콕시터 다이어그램 | |
| 세포 | r{3,6} {6,3} |
| 얼굴 | 삼각형 {3} 육각형 {6} |
| 정점수 |  삼각 프리즘 |
| 콕시터군 | [3,6,3] } [6,3[3]] 3 [3[3,3]] |
| 특성. | 정점 변환, 에지 변환 |
정류된 삼각형 타일링 벌집 , 는 삼각 프리즘 꼭지점과 함께 3헥각형 타일링과 육각형 타일링 셀을 가지고 있다.
대칭
이 벌집의 더 낮은 대칭은 통조림-6각형 타일링 벌집으로서 건설될 수 있다. 두 번째 낮은 지수 건설은 파운드다.
잘린 삼각 타일링 벌집
| 잘린 삼각 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | t{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | t{3,6} {6,3} |
| 얼굴 | 육각형 {6} |
| 정점수 | 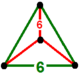 사면체 |
| 콕시터군 | [3,6,3] [3,3,6] |
| 특성. | 정규 |
잘린 삼각형 타일링 벌집 , 는 육각형 타일링 벌집의 낮은 대칭 형태로서, 4면 정점인 육각 타일링 면을 포함하고 있다.
삼각형 타일링 벌집
| 삼각형 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | 2t{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | t{6,3} |
| 얼굴 | 삼각형 {3} 도데카곤 {12} |
| 정점수 | 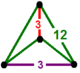 사방형 분산형 |
| 콕시터군 | [3,6,3] |
| 특성. | 정점 변환, 에지 변환, 셀 변환 |
잘린 삼각형 타일링 벌집, 은 6각형 타일링 셀을 가지고 있으며, 4각형 분산 정점 형상을 가지고 있다.
삼각형 타일링 벌집
| 삼각형 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | rr{3,6,3} 또는 t0,2{3,6,3} s2{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | rr{6,3} r{6,3} {}×{3} |
| 얼굴 | 삼각형 {3} 정사각형 {4} 육각형 {6} |
| 정점수 |  쐐기를 박다 |
| 콕시터군 | [3,6,3] |
| 특성. | 정점 변환 |
통조림 삼각형 타일링 벌집, 은 rhombitrihexangular tiling, 3hexangular tiling, 삼각 프리즘 셀을 가지고 있으며 쐐기 꼭지점 모양을 하고 있다.
대칭
그것은 또한 대칭이 있는 반대칭 형태의 삼각형 타일링 벌집, , 캔틱 스너브 삼각형 타일링 벌집으로 구성될 수 있다[3+,6,3].
캔티트런 삼각 타일링 벌집
| 캔티트런 삼각 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | tr{3,6,3} 또는 t0,1,2{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | tr{6,3} t{6,3} {}×{3} |
| 얼굴 | 삼각형 {3} 정사각형 {4} 육각형 {6} 도데카곤 {12} |
| 정점수 | 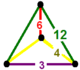 거울에 비친 스페노이드 |
| 콕시터군 | [3,6,3] |
| 특성. | 정점 변환 |
칸티트런으로 절단된 삼각형 타일링 벌집, 은 3헥사사각형 타일링, 잘린 육각 타일링, 삼각 프리즘 셀을 가지고 있으며, 미러링된 스페노이드 정점 형상을 가지고 있다.
삼각 타일링 벌집
| 삼각 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | t0,3{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | {3,6} {}×{3} |
| 얼굴 | 삼각형 {3} 정사각형 {4} |
| 정점수 | 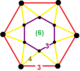 육각 항정신병 |
| 콕시터군 | [3,6,3] |
| 특성. | 정점 변환, 에지 변환 |
윤활된 삼각 타일링 벌집 , 는 삼각 타일링과 삼각 프리즘 셀을 가지고 있으며, 육각형 항정신병 정점 형상을 가지고 있다.
윤활 삼각 타일링 벌집
| 윤활 삼각 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | t0,1,3{3,6,3} s2,3{3,6,3} |
| 콕시터 도표 | |
| 세포 | t{3,6} rr{3,6} {}×{3} {}×{6} |
| 얼굴 | 삼각형 {3} 정사각형 {4} 육각형 {6} |
| 정점수 | 이소체-트라페지오이드의 피라미드를 짓다 |
| 콕시터군 | [3,6,3] |
| 특성. | 정점 변환 |
시계가 잘린 삼각형 타일링 벌집, 은 육각형 타일링, 광각형 타일링, 삼각 프리즘, 육각형 프리즘 셀을 가지고 있으며, 이소체-사다리꼴 피라미드 꼭지 모양을 하고 있다.
대칭
그것은 또한 대칭이 있는 반대칭 형태의 삼각형 타일링 벌집, , 로 구성될 수 있다[3+,6,3].
잡동사니 삼각 타일링 벌집
| 잡동사니 삼각 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 균일 벌집 |
| 슐레플리 기호 | t0,1,2,3{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | tr{3,6} {}×{6} |
| 얼굴 | 정사각형 {4} 육각형 {6} 도데카곤 {12} |
| 정점수 | 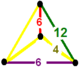 식물성 분산체 |
| 콕시터군 | [3,6,3] |
| 특성. | 정점 변환, 에지 변환 |
잡동사니 모양의 삼각형 타일링 벌집 은 3헥각형 타일링과 육각 프리즘 세포가 잘려나가며, 식물성 분산형 꼭지점이 있다.
삼각형 타일링 벌집
| 삼각형 타일링 벌집 | |
|---|---|
| 유형 | 파라콤팩트 메스폼 벌집 |
| 슐레플리 기호 | s3{3,6,3} |
| 콕시터 다이어그램 | |
| 세포 | r{6,3} {}x{3} {3,6} 트라이크업 |
| 얼굴 | 삼각형 {3} 정사각형 {4} 육각형 {6} |
| 정점수 | |
| 콕시터군 | [3+,6,3] |
| 특성. | 정점 변환, 균일하지 않음 |
삼각형 타일링 벌집 , 는 3헥각형 타일링, 삼각 타일링, 삼각 프리즘, 삼각 큐폴라 셀을 가지고 있다.존슨 고체 삼각 큐폴라 세포를 포함하고 있기 때문에 정점 변환이지만 균일하지는 않다.
참고 항목
참조
- Coxeter, 일반 폴리토페즈, 3번째, Dover Publishments, 1973. ISBN0-486-61480-8. (테이블 I 및 II: 일반 폴리탑 및 허니컴, 페이지 294–296)
- 기하학의 아름다움: 12개의 에세이(1999), 도버 출판물, LCCN 99-35678, ISBN 0-486-40919-8 (10장, 쌍곡 공간의 일반 허니컴) 표 III
- 제프리 R. Weeks The Shape of Space, 제2판 ISBN 0-8247-0709-5 (16-17장: 3-manifolds I,II)
- 노먼 존슨유니폼 폴리토페스, 원고
- N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
- N.W. 존슨: 기하학과 변환, (2018) 13장: 쌍곡선 콕시터 그룹