브래그의 법칙

물리학과 화학에서 브래그의 법칙, 울프-브라그의 조건 또는 라우에-브라그 간섭, 라우에 회절의 특별한 경우는 큰 결정 격자에서 파동의 일관된 산란을 위한 각도를 제공합니다. 이는 격자 평면에 의해 산란되는 파면의 중첩을 포함하여 파장과 산란각 사이의 엄격한 관계를 유도하거나, 그렇지 않으면 결정 격자에 대한 파동 벡터 전달을 유도합니다. 이러한 법칙은 처음에는 결정체에 대한 X선을 위해 공식화되었습니다. 하지만 원자 수가 많으면 원자 거리의 중성자파, 전자파 등 모든 종류의 양자 빔에 적용되며, 인공 주기 마이크로스케일 격자가 있는 가시광선에도 적용됩니다.

역사

브래그 회절(X선^[1] 회절의 브래그 공식이라고도 함)은 1913년 로렌스 브래그와 그의 아버지 윌리엄 헨리 브래그가 결정질 고체가 반사된 X선의 놀라운 패턴을 생성한다는 것을 발견한 것에 대한 반응으로 처음 제안했습니다. 그들은 특정한 파장과 입사각에서 이 결정들이 반사된 방사선의 강렬한 피크를 생성한다는 것을 발견했습니다. 파생된 브래그의 법칙은 라우에 회절에 대한 특별한 해석으로, 브래그는 결정 격자 평면에서 나오는 파동의 반사에 의해 기하학적인 방식으로 건설적인 라우에-브래그 간섭을 해석하여 경로-차이가 입사 파장의 배수가 됩니다.

로렌스 브래그(Lawrence Bragg)는 이 결과를 상수 $매개변수$ d로 분리된 이산 평행면의 집합으로 모델링하여 설명했습니다. 다양한 평면에서 반사되는 것이 건설적으로 간섭한다면 입사 X선 방사선이 브래그 피크를 생성할 것이라고 제안되었습니다. 위상 이동이 $2$ π의 배수일 때 간섭은 건설적입니다. 이 조건은 브래그의 법칙에 의해 표현될 수 있으며(아래 브래그 조건 부분 참조) 1912년 11월 11일 로렌스 브래그가 케임브리지 철학 학회에 처음 발표했습니다. 비록 간단하지만 브래그의 법칙은 원자 규모에서 실제 입자의 존재를 확인했을 뿐만 아니라 X선과 중성자 회절의 형태로 결정을 연구하는 강력한 새로운 도구를 제공했습니다. 로렌스 브래그(Lawrence Bragg)와 그의 아버지 윌리엄 헨리 브래그(William Henry Bragg)는 1915년 NaCl, ZnS, 다이아몬드로 시작하는 결정 구조를 결정한 공로로 노벨 물리학상을 수상했습니다. 그들은 공동으로 우승한 유일한 부자 팀입니다.

브래그 회절의 개념은 중성자 회절에도 동일하게 적용되며, 전자 회절에도 거의 동일하게 적용됩니다.^[4] 이 모든 것에서 파장은 원자간 거리(~ 150pm)와 비슷하므로 이 길이 척도에 적합한 프로브입니다. 많은 다른 유형의 물질파도 회절하는 것으로 나타났습니다.

브래그 상태

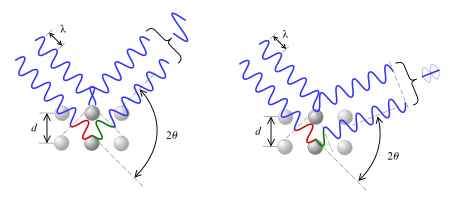
브래그 회절은 원자 간격과 비슷한 $파장$ 의 λ의 복사가 결정계의 원자에 의해 특정한 방식으로 산란되어(거울과 같은 반사) 건설적인 간섭을 받을 때 발생합니다. 결정질 고체의 경우 파동은 연속적인 원자 층 사이의 거리 $d만큼$ 떨어진 격자면에서 산란됩니다.^[6]^{: 223} 흩어진 파동들이 건설적으로 간섭할 때 그들은 위상을 유지합니다. 이들은 표면에 일정한 각도로 부딪힐 때만 반사됩니다. ( $오른쪽$ 그림 참조) θ은 θ을 표면 법선으로부터 측정하는 스넬의 $법칙$ 과 다르며, 파장 λ $및$ 결정의 "격자 상수" $d$ 는 다음 관계에 의해 연결됩니다.

n\lambda =2d\sin \theta

n

is the diffraction order (

n=1

is first order,

n=2

is second order,^[6]^{: 221}

n=3

is third order^[7]^{: 1028}). 결정 격자의 연속적인 결정학적 평면(h,k,l)에서의 반사의 누적 효과로 인해 건설적 또는 파괴적 간섭의 효과가 심화됩니다(Miller 표기법에 의해 설명됨). 이는 θ의 건설적 간섭이 가장 강력한 조건을 설명하는 브래그의 법칙으로 이어집니다.

산란각의 함수로 산란파의 세기를 측정하여 회절 패턴을 얻습니다. 회절 패턴은 산란각이 브래그 조건을 만족할 때 브래그 피크로 알려진 강한 강도가 얻어집니다. 서론에서 언급한 바와 같이, 이 조건은 보다 일반적인 Laue 방정식의 특수한 경우이며, Laue 방정식은 추가적인 가정 하에서 브래그 조건으로 감소하는 것을 보여줄 수 있습니다.

산란공정 보강

X선이 원자에 입사하면 전자 구름을 움직이게 하고, 전자파도 마찬가지입니다. 이러한 전하의 이동은 다양한 영향으로 인해 약간 흐려진 동일한 주파수의 파동을 재방사합니다. 이러한 현상을 레일리 산란(또는 탄성 산란)이라고 합니다. 산란되는 파동 자체는 산란될 수 있지만 이 2차 산란은 무시할 수 있다고 가정합니다.

유사한 과정은 중성자파를 핵에서 산란시키거나 짝을 이루지 않은 전자와의 일관된 스핀 상호작용에 의해 발생합니다. 이러한 재방출 파동장은 건설적 또는 파괴적으로 서로 간섭합니다(겹침파는 서로 합쳐져서 더 강한 피크를 생성하거나 서로 어느 정도 차감됨). 검출기 또는 필름에 회절 패턴을 생성합니다. 결과적인 파동 간섭 패턴은 회절 분석의 기초가 됩니다. 이 분석을 브래그 회절이라고 합니다.

휴리스틱 유도

$d$ 단색파가 $\theta$ θ ${\displaystyle$ $\theta$ \theta $\theta$ $d$ 각도에서 분리된 {\displaystyle $d}$ 개의 격자점들의 정렬된 평면에 입사한다고 가정하자. 점 A와 C는 한 평면에 있고, B는 아래 평면에 있습니다. 점 ABCC'는 4각형을 형성합니다.

AC'를 따라 반사되는 광선과 AB를 따라 투과된 후 BC를 따라 반사되는 광선 사이에는 경로 차이가 있을 것입니다. 이 경로 차이는

{\displaystyle(AB+BC)-\left(AC'\right)\,}

두 개의 분리된 파동은 동일한 위상을 가진 한 지점(이 격자 평면에서 무한히 변위됨)에 도달하므로 이 경로 차이가 파장의 정수 값과 동일한 경우에만 보강 간섭을 받게 됩니다.

n\lambda =(AB+BC)-\left(AC'\right)

여기서 $n$ $n$ 및 $\lambda$ λ ${\displaystyle$ \ lambda }는 각각 정수 및 입사파의 파장입니다.

그러므로,

AB=BC={\frac {d}{\sin \theta }}{\text{ and }}AC={\frac {2d}{\tan \theta }}\,,

그 후의 일로

AC'=AC\cdot \cos \theta ={\frac {2d}{\tan \theta }}\cos \theta =\left({\frac {2d}{\sin \theta }}\cos \theta \right)\cos \theta ={\frac {2d}{\sin \theta }}\cos ^{2}\theta \,.

모든 것을 종합해 보면,

n\lambda ={\frac {2d}{\sin \theta }}-{\frac {2d}{\sin \theta }}\cos ^{2}\theta ={\frac {2d}{\sin \theta }}\left(1-\cos ^{2}\theta \right)={\frac {2d}{\sin \theta }}\sin ^{2}\theta

위에 표시된 브래그의 법칙인 $n\lambda =2d\sin \theta \,,$ λ = 2d sin lambda , ${\$ displaystyle n\⁡ θ = 2d\sin \theta \...}로 단순화됩니다.

만약 그림과 같이 두 개의 원자 평면만이 회절한다면, 보강 간섭에서 파괴 간섭으로의 전환은 각도의 함수로서 점진적일 것이고, 브래그 각도에서 완만하게 최대가 될 것입니다. 그러나 대부분의 실제 물질에는 많은 원자 평면이 간섭에 참여하고 있기 때문에 대부분 파괴적인 간섭으로 둘러싸인 매우 날카로운 피크가 발생합니다.^[9]

보다 일반적인 Laue 방정식에서 엄밀한 유도를 사용할 수 있습니다(페이지 참조: 라우 방정식).

브래그의 법칙을 넘어서

일반적으로 선택된 영역 전자 회절 패턴입니다. 각 지점은 서로 다른 회절 방향에 해당합니다.

브래그 조건은 매우 큰 결정에 적합합니다. X선과 중성자의 산란이 상대적으로 약하기 때문에 크기가 100nm 이상인 상당히 큰 결정을 사용하는 경우가 많습니다. 결정 결함으로 인해 추가적인 영향이 있을 수 있지만, 이들은 종종 상당히 작습니다. 반대로 전자는 X선보다 고체와 수천 배 더 강하게 상호작용하고,^[4] 에너지도 손실합니다(비탄성 산란).^[10] 따라서 투과 전자 회절에 사용되는 샘플은 훨씬 얇습니다. 그림과 같은 일반적인 회절 패턴은 결정을 떠나는 전자의 다른 방향(평면파)에 대한 점을 보여줍니다. 브래그의 법칙이 예측하는 각도는 여전히 대략적으로 옳지만, 일반적으로 전자빔의 방향에 직각인 역격자의 투영에 가까운 점들의 격자가 존재합니다. (이에 반해 브래그의 법칙은 동시에 수십~수백 개가 아니라 한 개 또는 두 개만 존재할 것으로 예측합니다.) 일반적으로 전자 에너지가 30-1000 전자 볼트인 저에너지 전자 회절의 경우 표면에서 반사된 전자와 결과가 비슷합니다.^[11] 또한 일반적으로 회절 반점의 고리로 이어지는 반사 고에너지 전자 회절도 유사합니다.^[12]

X선을 사용하면 작은 결정을 갖는 효과는 셔러 방정식으로 설명됩니다.^[13]^[14]^[15] 이로 인해 결정의 크기를 추정하는 데 사용할 수 있는 브래그 피크가 넓어집니다.

콜로이드에 의한 가시광선의 브래그 산란

콜로이드 결정(colloidal crystal)은 긴 범위(길이가 수 밀리미터에서 1 센티미터)에 걸쳐 형성되는 입자의 정렬된 배열입니다. 콜로이드 결정은 원자 또는 분자와 거의 유사한 모양과 특성을 가지고 있습니다.^[16] 반발적인 쿨롱 상호작용으로 인해 수성 환경에서 전기적으로 대전된 거대분자는 긴 범위의 결정과 같은 상관관계를 나타낼 수 있으며, 종종 입자간 분리 거리가 개별 입자 직경보다 상당히 크다는 것이 수년 전부터 알려져 왔습니다. 구면 입자의 주기적 배열은 입사 광파와 크기가 같은 경우 가시 광파의 자연 회절 격자 역할을 하는 간공극(입자 사이의 공간)을 발생시킵니다.^[17]^[18]^[19] 자연에서 이러한 경우, 밝은 적외선(또는 색의 재생)은 결정성 고체에서 X선이 산란되는 것과 유사한 문제에서 브래그의 법칙에 따라 가시 광선의 회절과 보강 간섭에 기인합니다. 분리 파라미터 $d$ 가 실제 결정보다 훨씬 크기 때문에 가시 파장에서 효과가 발생합니다. 프레셔스 오팔은 콜로이드 결정이 눈에 띄는 광학 효과를 내는 한 예입니다.

볼륨 브래그 격자

볼륨 브래그 격자(VBG) 또는 볼륨 홀로그램 격자(VHG)는 굴절률에 주기적인 변화가 있는 볼륨으로 구성됩니다. 굴절률의 변조 방향에 따라 파장의 작은 대역폭을 전송하거나 반사하는 데 VBG를 사용할 수 있습니다.^[20] (볼륨 홀로그램에 맞게 조정된) 브래그의 법칙은 어떤 파장이 회절될 것인지를 결정합니다.^[21]

2\Lambda \sin(\theta +\varphi )=m\lambda _{B}\,

여기서 $m$ 은 브래그 차수(양의 정수), 회절파장 λ, 격자의 프린지 간격 λ, 입사빔과 $입구면$ 의 법선(N) 사이의 각도를 θ하고 $법선과$ 격자벡터(K) 사이의 각도를 φ합니다. 브래그의 법칙과 일치하지 않는 방사선은 VBG를 회절하지 않고 통과할 것입니다. 입사각(θ)을 변경하여 출력 파장을 수백 나노미터 이상 조정할 수 있습니다. VBG는 광범위하게 조정 가능한 레이저 소스를 생성하거나 전역 초분광 영상을 수행하는 데 사용되고 있습니다(Photon 등 참조).

선택 규칙 및 실용 결정학

브래그의 법칙은 위에서 언급한 바와 같이 다음 관계를 통해 특정 입방체계의 격자 간격을 구할 수 있습니다.

d={\frac {a}{\sqrt {h^{2}+k^{2}+\ell ^{2}}}}\,,

$a$ 서 $a$ 는 입방정의 격자 간격이고, $h$ , $k$ , ℓ은 브래그 평면의 밀러 지수입니다. 이 관계를 브래그의 법칙과 결합하면 다음과 같은 결과를 얻을 수 있습니다.

\left ({\frac {\lambda }{2a}}\right)^{2}=\left ({\frac {\lambda }{2d}}\right)^{\frac {1}{h^{2}+k^{2}+\ell ^{2}}}

서로 다른 입방 Bravais 격자에 대한 Miller 지수에 대한 선택 규칙을 도출할 수 있습니다. 여기서는 여러 개에 대한 선택 규칙이 그대로 주어집니다.

Miller 지수의 선택 규칙
브라바리스 라떼	예시 화합물	반사 허용	금지된 반사
심플 큐빅	포	아무어, ㅋ, ㅋ.	없음.
체심입방	Fe,W,Ta,Cr	h + k + ℓ = 짝수	h + k + ℓ = 홀수
얼굴중심입방(FCC)	Cu, Al, Ni, NaCl, LiH, PbS	h, k, ℓ이 모두 이상하거나 짝수인	h, k, 홀수와 짝수가 섞인 ℓ
다이아몬드 FCC	시, 게	h + k + ℓ = 4n인 홀수 또는 짝수	h, k, 홀수와 짝수가 혼합된 ℓ 또는 모두 h + k + ℓ ≠ 4n
삼각격자	Ti, Zr, Cd, Be	ℓ even, h + 2k ≠ 3n	h + 2k = 3n for odd ℓ

이러한 선택 규칙은 주어진 결정 구조를 가진 모든 결정에 사용할 수 있습니다. KCl은 면심 입방정 Bravais 격자를 가지고 있습니다. 그러나⁺ K와 Cl⁻ 이온은 전자의 수가 같고 크기가 상당히 가깝기 때문에 회절 패턴은 격자 파라미터가 절반인 단순한 입방 구조의 경우와 본질적으로 같아집니다. 다른 구조물에 대한 선택 규칙은 다른 곳에서 참조하거나 유도할 수 있습니다. 다른 결정 시스템에 대한 격자 간격은 여기에서 확인할 수 있습니다.

참고 항목

참고문헌

^ Bragg, W. H.; Bragg, W. L. (1913). "The Reflexion of X-rays by Crystals". Proc. R. Soc. Lond. A. 88 (605): 428–38. Bibcode:1913RSPSA..88..428B. doi:10.1098/rspa.1913.0040. S2CID 13112732.
^ 예를 들어, 이 예제 계산은 2011년 7월 10일에 Wayback Machine에서 Bragg의 법칙을 적용한 원자간 거리 측정 방법을 참조하십시오.
^ 이 법칙의 발견을 W.L 브래그와 그의 아버지 W.H. 브래그의 탓으로 돌리는 학술 미국 백과사전과 같은 자료들이 있습니다. 그러나 공식적인 노벨상 사이트와 그에 대해 쓰여진 전기("Light Is a Messenger: 빛은 메신저입니다. 윌리엄 로렌스 브래그의 삶과 과학", 그레임 K. Hunter, 2004, "20세기의 위대한 고체 상태 물리학자" Julio Antonio Gonzalo, Carmen Aragó López)는 로렌스 브래그가 단독으로 이 법칙을 도출했다고 분명히 밝혔습니다.
^ ^a ^b 존 엠. 카울리 (1975) 회절 물리학 (North-Holland, 암스테르담) ISBN 0-444-1071-6.
^ Bragg, Henry W.; Bragg, Lawrence W. (January 1915), G. Bell and sons L.T.D. London (ed.), X RAYS AND CRYSTAL STRUCTURE, p. 228, retrieved 2021-05-12
^ ^a ^b Moseley, Henry H. G. J.; Darwin, Charles G. (July 1913). "on the Reflexion of the X-rays". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 210–232. doi:10.1080/14786441308634968. Retrieved 2021-04-27.
^ ^a ^b Moseley, Henry G. J. (1913). Smithsonian Libraries. "The High-Frequency Spectra of the Elements". The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science. 6. London-Edinburgh: London : Taylor & Francis. 26: 1024–1034. doi:10.1080/14786441308635052.
^ H. P. Myers (2002). Introductory Solid State Physics. Taylor & Francis. ISBN 0-7484-0660-3.
^ "x-ray diffraction, Bragg's law and Laue equation". electrons.wikidot.com.
^ Egerton, R. F. (2009). "Electron energy-loss spectroscopy in the TEM". Reports on Progress in Physics. 72 (1): 016502. Bibcode:2009RPPh...72a6502E. doi:10.1088/0034-4885/72/1/016502. S2CID 120421818.
^ Moritz, Wolfgang; Van Hove, Michel (2022). Surface structure determination by LEED and X-rays. Cambridge, United Kingdom. ISBN 978-1-108-28457-8. OCLC 1293917727.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)
^ Ichimiya, Ayahiko; Cohen, Philip (2004). Reflection high-energy electron diffraction. Cambridge, U.K.: Cambridge University Press. ISBN 0-521-45373-9. OCLC 54529276.
^ Scherrer, P. (1918). "Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. 1918: 98–100.
^ Patterson, A. L. (1939). "The Scherrer Formula for X-Ray Particle Size Determination". Physical Review. 56 (10): 978–982. Bibcode:1939PhRv...56..978P. doi:10.1103/PhysRev.56.978.
^ Warren, B. E. (1969). X-ray diffraction. Reading, Mass.: Addison-Wesley Pub. Co. ISBN 0-201-08524-0. OCLC 21564.
^ Pieranski, P (1983). "Colloidal Crystals". Contemporary Physics. 24: 25–73. Bibcode:1983ConPh..24...25P. doi:10.1080/00107518308227471.
^ Hiltner, PA; IM Krieger (1969). "Diffraction of Light by Ordered Suspensions". Journal of Physical Chemistry. 73 (7): 2386–2389. doi:10.1021/j100727a049.
^ Aksay, IA (1984). "Microstructural Control through Colloidal Consolidation". Proceedings of the American Ceramic Society. 9: 94.
^ Luck, Werner; Klier, Manfred; Wesslau, Hermann (1963). "Über Bragg-Reflexe mit sichtbarem Licht an monodispersen Kunststofflatices. II". Berichte der Bunsengesellschaft für physikalische Chemie. 67 (1): 84–85. doi:10.1002/bbpc.19630670114. ISSN 0005-9021.
^ Barden, S.C.; Williams, J.B.; Arns, J.A.; Colburn, W.S. (2000). "Tunable Gratings: Imaging the Universe in 3-D with Volume-Phase Holographic Gratings (Review)". ASP Conf. Ser. 195: 552. Bibcode:2000ASPC..195..552B.
^ C. Kress, Bernard (2009). Applied Digital Optics : From Micro-optics to Nanophotonics. ISBN 978-0-470-02263-4.

외부 링크

[1] Bragg, W. H.; Bragg, W. L. (1913). "The Reflexion of X-rays by Crystals". Proc. R. Soc. Lond. A. 88 (605): 428–38. Bibcode:1913RSPSA..88..428B. doi:10.1098/rspa.1913.0040. S2CID 13112732.

[2] 예를 들어, 이 예제 계산은 2011년 7월 10일에 Wayback Machine에서 Bragg의 법칙을 적용한 원자간 거리 측정 방법을 참조하십시오.

[3] 이 법칙의 발견을 W.L 브래그와 그의 아버지 W.H. 브래그의 탓으로 돌리는 학술 미국 백과사전과 같은 자료들이 있습니다. 그러나 공식적인 노벨상 사이트와 그에 대해 쓰여진 전기("Light Is a Messenger: 빛은 메신저입니다. 윌리엄 로렌스 브래그의 삶과 과학", 그레임 K. Hunter, 2004, "20세기의 위대한 고체 상태 물리학자" Julio Antonio Gonzalo, Carmen Aragó López)는 로렌스 브래그가 단독으로 이 법칙을 도출했다고 분명히 밝혔습니다.

[:0-4] 존 엠. 카울리 (1975) 회절 물리학 (North-Holland, 암스테르담) ISBN 0-444-1071-6.

[bragg-5] Bragg, Henry W.; Bragg, Lawrence W. (January 1915), G. Bell and sons L.T.D. London (ed.), X RAYS AND CRYSTAL STRUCTURE, p. 228, retrieved 2021-05-12

[moseley1913a-6] Moseley, Henry H. G. J.; Darwin, Charles G. (July 1913). "on the Reflexion of the X-rays". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (151): 210–232. doi:10.1080/14786441308634968. Retrieved 2021-04-27.

[Mose1913-7] Moseley, Henry G. J. (1913). Smithsonian Libraries. "The High-Frequency Spectra of the Elements". The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science. 6. London-Edinburgh: London : Taylor & Francis. 26: 1024–1034. doi:10.1080/14786441308635052.

[8] H. P. Myers (2002). Introductory Solid State Physics. Taylor & Francis. ISBN 0-7484-0660-3.

[9] "x-ray diffraction, Bragg's law and Laue equation". electrons.wikidot.com.

[10] Egerton, R. F. (2009). "Electron energy-loss spectroscopy in the TEM". Reports on Progress in Physics. 72 (1): 016502. Bibcode:2009RPPh...72a6502E. doi:10.1088/0034-4885/72/1/016502. S2CID 120421818.

[11] Moritz, Wolfgang; Van Hove, Michel (2022). Surface structure determination by LEED and X-rays. Cambridge, United Kingdom. ISBN 978-1-108-28457-8. OCLC 1293917727.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)

[12] Ichimiya, Ayahiko; Cohen, Philip (2004). Reflection high-energy electron diffraction. Cambridge, U.K.: Cambridge University Press. ISBN 0-521-45373-9. OCLC 54529276.

[13] Scherrer, P. (1918). "Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. 1918: 98–100.

[14] Patterson, A. L. (1939). "The Scherrer Formula for X-Ray Particle Size Determination". Physical Review. 56 (10): 978–982. Bibcode:1939PhRv...56..978P. doi:10.1103/PhysRev.56.978.

[15] Warren, B. E. (1969). X-ray diffraction. Reading, Mass.: Addison-Wesley Pub. Co. ISBN 0-201-08524-0. OCLC 21564.

[Pieranski_1983-16] Pieranski, P (1983). "Colloidal Crystals". Contemporary Physics. 24: 25–73. Bibcode:1983ConPh..24...25P. doi:10.1080/00107518308227471.

[Hiltner_1969-17] Hiltner, PA; IM Krieger (1969). "Diffraction of Light by Ordered Suspensions". Journal of Physical Chemistry. 73 (7): 2386–2389. doi:10.1021/j100727a049.

[Aksay_1984-18] Aksay, IA (1984). "Microstructural Control through Colloidal Consolidation". Proceedings of the American Ceramic Society. 9: 94.

[LuckKlier1963-19] Luck, Werner; Klier, Manfred; Wesslau, Hermann (1963). "Über Bragg-Reflexe mit sichtbarem Licht an monodispersen Kunststofflatices. II". Berichte der Bunsengesellschaft für physikalische Chemie. 67 (1): 84–85. doi:10.1002/bbpc.19630670114. ISSN 0005-9021.

[20] Barden, S.C.; Williams, J.B.; Arns, J.A.; Colburn, W.S. (2000). "Tunable Gratings: Imaging the Universe in 3-D with Volume-Phase Holographic Gratings (Review)". ASP Conf. Ser. 195: 552. Bibcode:2000ASPC..195..552B.

[21] C. Kress, Bernard (2009). Applied Digital Optics : From Micro-optics to Nanophotonics. ISBN 978-0-470-02263-4.

[1]

[4]

[5]

[6]

[7]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

Search