압축성인자

열역학
클래식 카르노 열기관
나뭇가지 고전적인 통계적 케미컬 양자 열역학 평형/비평형
법 제롯 먼저 둘째 세 번째
시스템들 폐쇄형 시스템 절연계통 주 상태 방정식 이상기체 리얼 가스 물질 상태 위상(물질) 평형 제어량 계기 과정 이소바르어 이소차리아어 등온 아디아바틱 등방성 이센탈픽 콰지스타틱 다항성 자유팽창 가역성 불가역성 내재해성 사이클 열기관 열펌프 열효율
시스템 속성 참고: 이탤릭체의 결합 변수 특성 다이어그램 집약적이고 광범위한 속성 공정함수 일 열 국가의 기능 온도 / 엔트로피(소개) 압력/볼륨 화학전위/입자수 증기 품질 감소된 특성
재료 특성 속성 데이터베이스 특정 열 용량 ${\displaystyle c=}$ $T}$ $\displaystyle \partial S}$ ${\디스플레이 스타일 N}$ $\displaystyle \partial T}$ 압축성 ${\displaystyle \cHB =-}$ ${\displaystyle 1}$ $\displaystyle \partial V}$ $(\displaystyle V}$ $\displaystyle \displayp p}$ 열팽창 ${\displaystyle \cHB =}$ ${\displaystyle 1}$ $\displaystyle \partial V}$ $(\displaystyle V}$ $\displaystyle \partial T}$
방정식 카르노의 정리 클로스 정리 근본관계 이상기체법 맥스웰 관계 온사저 호혜 관계 브리그만 방정식 열역학 방정식 표
가능성 자유 에너지 자유 엔트로피 내부 에너지 ${\displaystyle U(S,V)}$ 엔탈피 ${\displaystyle H(S,p)=U+pV}$ 헬름홀츠 자유 에너지 $A(T,V)=U-TS}$ 기브스 자유 에너지 $(\displaystyle G(T,p)=H-TS}$
역사 문화 역사 일반 엔트로피 가스법칙 "주기적 운동" 기계 철학 엔트로피와 시간 엔트로피와 생명 브라운 래칫 맥스웰의 악마 열사 역설 로슈미트의 역설 시너게틱스 이론들 칼로리 이론 Vis viva ("생존력") 열과 기계적 등가 원동력 주요 출판물 "실험적 질문 컨서닝 ... 열" "이종균질 물질의 평형성에 대하여" "불의 모티브 파워에 대한 반향" 타임라인 열역학 열기관 예술 , 교육 맥스웰의 열역학적 표면 에너지 분산으로서의 엔트로피
과학자들 베르누이 볼츠만 카르노 클라피론 클라우시우스 캐러테오도리 듀헴 깁스 폰 헬름홀츠 줄 맥스웰 폰 마이어 온사거 플랑크 랭킨 스마톤 스타울 톰프슨 톰슨 판데르 발스 워터스턴
기타 핵 자가 조립 자기 조직화 질서와 무질서
카테고리
v t

열역학에서 압축 계수 또는 기체 편차 계수로도 알려진 압축성 계수(Z)는 이상적인 기체 거동에 대한 실제 기체의 편차를 설명하는 보정 계수다. 단순히 동일한 온도와 압력에서 이상적인 기체의 어금니 부피 대비 기체의 어금니 부피의 비율로 정의된다. 그것은 실제 가스 행동을 설명하기 위해 이상적인 가스 법칙을 수정하는 데 유용한 열역학적 특성이다.^[1] 일반적으로 이상적인 행동으로부터의 편차는 기체가 위상 변화에 가까울수록, 온도가 낮거나 압력이 클수록 더 중요해진다. 압축성 계수 값은 일반적으로 복합 특이 경험 상수를 입력으로 사용하는 처녀 방정식과 같은 상태 방정식(EOS)에서 계산하여 얻는다. 둘 이상의 순수 가스(예를 들어 공기 또는 천연 가스)가 혼합된 기체의 경우, 압축성을 계산하기 전에 가스 구성을 알아야 한다.
또는 특정 가스에 대한 압축성 계수는 $Z{\displaystyle }$ ${\displaystyle Z}$을(를) 일정한 온도에서 압력의 함수로 표시하는$$ 일반화된 압축성 차트에서^[1] 읽을 수 있다.

압축성 계수는 압축성(압축성 계수 또는 등온 압축성 계수라고도 함)과 혼동해서는 안 되며, 이는 압력 변화에 대응하는 유체 또는 고체의 상대적 부피 변화를 측정하는 척도다.

정의 및 물리적 중요성

압축성 계수는 열역학 및 엔지니어링에서 자주 다음과 같이 정의된다.

${\displaystyle Z={\frac {p}{\rho R_{\text{특정}}T}},}$

where p is the pressure, ${\displaystyle \rho }$ is the density of the gas and ${\displaystyle R_{\text{specific}}={\frac {R}{M}}}$ is the specific gas constant,^[2] ${\displaystyle M}$ being the molar mass, and the ${\displaystyle T}$ is the absolute temperature (Kelvin or Rankine scale).

통계 역학에서 설명은 다음과 같다.

${\displaystyle Z={\frac {pV}{nnRT},}$

여기서 p는 압력, n은 기체의 두더지 수, $T{\displaystyle }$ ${\displaystyle T}$은 절대 온도, $R{\displaystyle }$ ${\displaystyle R}$은 기체 상수다.

이상적인 기체의 경우 압축성 계수는 정의당$$ ${\displaystyle \mathrm{Z}}$= 1 ${\displaystyle Z=1}$이다. 많은 실제 세계에서 정확성에 대한 애플리케이션 요건은 이상적인 가스 행동, 즉 실제 가스 행동으로부터의 편차를 고려해야 한다고 요구한다. $Z{\displaystyle }$ ${\displaystyle Z}$의 값은 일반적으로$$ 압력에 따라 증가하고 온도에 따라 감소한다. 고압에서는 분자가 더 자주 충돌한다. 이를 통해 분자 간의 반발력이 눈에 띄는 효과를 낼 수 있어 실제 기체의 어금니 부피(${\displaystyle {Vm\mathrm{}}_{}}$ ${\$가 해당 ${\displaystyle {\text{이상 기체}}_{}}$의 어금니 부피${\displaystyle {}_{}{Vm}_{}{}_{}}$ = ${\displaystyle R}$ T${\displaystyle }$/ ${\displaystyle p}$ ${\displaystyle (V_{m}}}}}}}}{\text{ideal gas}=}}}}}}}}}}}}})$보다 커진다.$Z{\displaystyle }$ ${\displaystyle Z}$이(가)^[3] 1을 초과하게$$ $하는$RT/$p}$ $$). 압력이 낮아지면 분자는 자유롭게 움직일 수 있다. 이 경우 매력적인 힘이 지배하여 < $>을 만든다$ 기체가 임계점이나 비등점에 가까울수록 $Z{\displaystyle }$ ${\displaystyle Z}$이(가) 이상적인 케이스에서 벗어나게$$ 된다.

도망성

압축성 계수는 관계에^{[citation needed]} 의해 도망성과 연결된다.

${\displaystyle f=P\exp \left(\int {\frac {Z-1}{P}dP\right)}$

순수 가스에 대한 일반화된 압축성 계수 그래프

압축성 인자와 감소된 온도 사이의 ${\displaystyle {고유}_{}}$한 관계인$$T r {\$displaystyle$ T_${r$와 감소된 압력인 ${\displaystyle P_{}}$ $r{\displaystyle {}_{}}$ ${\$는 1873년 요하네스 디데릭 반 데르 바알스에 의해 처음 인정되어 해당 상태의 2변수 원리로 알려져 있다. 해당 상태의 원리는 분자간 힘에 의존하는 기체의 성질이 기체의 임계적 성질과 관련이 있다는 일반화를 보편적으로 표현하고 있다. 그것은 분자 성질의 상관관계를 발전시키는데 가장 중요한 기초를 제공한다.

기체의 압축성에 관해서는, 해당 상태의 원리는 동일한 ${\displaystyle {감소온도}_{}}$ $T{\displaystyle {}_{}}$ r ${\$$r}$와 감소압력 $P{\displaystyle {}_{}}$ ${\displaystyle r_{}}$ ${\$에서 모든 순수$$기체는 동일한 압축률을 가져야 함을 나타낸다.

감소된 온도와 압력은 다음에 의해 정의된다.

${\$$T_{c}}}}$과(${\displaystyle {와}_{}}$ P r = ${\displaystyle P\frac{}{}}$ ${\displaystyle \frac{c_{}}{}}$. ${\displaystyle P_{r}={\frac {P}{P_{c}}}.$$}$

여기서 $T{\displaystyle {}_{}}$ ${\$와 $P{\displaystyle {}_{}}$ ${\displaystyle c_{}}$ ${\$는 기체의 임계온도와 임계압력으로 알려져$$ 있다. 각 특정 가스의 특성으로 T ${\displaystyle c_{}}$ ${\$는 특정 가스를 액화시킬 수 없는 온도 이상이고$$ $P{\displaystyle {}_{}}$ ${\displaystyle c_{}}$ ${\$는 해당$$ 가스를 임계 온도에서 액화하는데 필요한 최소 압력이다. 그들은 함께 주어진 액체의 뚜렷한 액체와 가스 단계가 존재하지 않는 위 액체의 임계점을 정의한다.

실제 가스에 대한 압력 용적 온도(PVT) 데이터는 순수 가스마다 다르다. 단, 다양한 단일 구성성분 기체의 압축성 인자를 그래프로 표시할 때 압력 대 온도 차이를 나타내는 그래프도 많다.

여러 가지 다른 기체에 사용할 수 있는 일반화된 그래프를 얻기 위해 감소된 압력 및 온도 $P{\displaystyle {}_{}}$ ${\displaystyle r_{}}$ ${\$ 및 $T$ ${\displaystyle r_{}}$ ${\$를 사용하여 압축성 인자 데이터를 정규화한다. 그림 2는 메탄, 에탄, 에틸렌, 에틸렌, 프로판, 엔부탄, 아이펜탄, 엔헥산, 질소, 이산화탄소, 증기 등 10개 순수 가스의 수백 개의 실험 PVT 데이터 지점에서 도출한 일반화된 압축성 인자 그래프의 예다.

넬슨-오버트 그래프와 같은 25개 이상의 순가스를 기반으로 한 보다 상세한 일반화된 압축성 인자 그래프가 있다. 이러한 그래프는 $0{\displaystyle }$.6보다 큰 Z ${\displaystyle Z}$ 값에$$ 대해서는 1~2%, 0.3~0.$6$의 Z$$$${\$displaystyle Z$} 값에 대해서는 4~6% 이내의 정확도를 갖는다고 한다.

일반화된 압축성 인자 그래프는 양전하 중심과 음전하 중심이 일치하지 않는 강한 극성 가스의 경우 상당한 오차가 있을 수 있다. 이러한 경우 $Z{\displaystyle }$ ${\displaystyle Z}$에 대한 추정치는 15~20% 정도 오류가 발생할 수 있다$$.

수소, 헬륨 및 네온의 양자 기체는 해당 상태 거동에 부합하지 않으며 세 기체에 대한 감소된 압력과 온도는 일반화된 그래프를 사용할 때 압축성 인자를 예측하는 정확도를 개선하기 위해 다음과 같이 재정의해야 한다.

${\$$T_{c}+8}}$과(${\displaystyle {와}_{}}$ ${\displaystyle \frac{P{}_{}}{}}$ r = P c$$+${\displaystyle \frac{{}_{}8}{}}$ {\$displaystyle P_{$r}={\$frac$ {$P}{$P_${c}+8}}}}}$

온도가 켈빈에 있고 압력이 대기 중에 있는 곳.^[4]

일반화 압축성 차트를 읽는 방법

압축성 차트를 읽으려면 감소된 압력과 온도를 알아야 한다. 감소된 압력 또는 온도를 알 수 없는 경우 감소된 특정 부피를 찾아야 한다. 감소된 압력 및 온도와 달리 감소된 특정 부피는 임계 부피를 사용하여 찾을 수 없다. 감소된 특정 볼륨은 다음에 의해 정의된다.

${\displaystyle \nu _{R}={\frac {\nu _{\text{actual}}}{\displaystyle \nu}}RT_{\text{cr}/P_{\text{cr}}}}$

여기서 $\nu {\displaystyle {}_{}}$ ${\displaystyle {\text{real}}_{}}$ ${\$은(는) 특정 볼륨이다$$.^[5]

감소된 특성 3개 중 2개가 발견되면 압축성 차트를 사용할 수 있다. 압축성 차트에서 감소된 압력은 x축에, Z는 y축에 있다. 감소된 압력 및 온도가 주어지면 X축에서 주어진 압력을 찾으십시오. 거기서 주어진 감소된 온도가 발견될 때까지 차트에서 위로 이동한다. Z는 그 두 점이 교차하는 곳을 보면 알 수 있다. 감소된 특정 부피가 압력 또는 온도 감소로 주어지는 경우에도 동일한 과정을 따를 수 있다.

일반화된 압축성 차트에서 만든 관측치

일반화된 압축성 차트를 볼 때 세 가지 관측치를 볼 수 있다. 이러한 관측치는 다음과 같다.

1. 가스는 감소된 압력이 1보다 훨씬 작을 때 온도에 관계없이 이상적인 기체로 작용한다(P_R< 1).
2. 감소된 온도가 2(T_R > 2)보다 크면 압력이 훨씬 크지 않은 한 압력과 관계없이 이상 가스 동작을 가정할 수 있다.
   1(P_R >> 1)보다.
3. 기체는 임계점 근처에서 가장 이상적인 기체 행동에서 벗어난다.^[6]

이론적 모델

처녀 방정식은 다음과 같은 통계적 역학에서 직접 도출되기 때문에 분자 수준에서 비이상성의 원인을 설명하는데 특히 유용하다.

${\displaystyle Z=1+{\frac {B}{V_{\matrm {m}}}}{V_{\matrm {m}^{2}}}+{\frac {D}{V_{{\matrm}{}}}}}}}{{{3}}}}}}}}}}+\dots}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.$

여기서 분자의 계수를 처녀계수라고 하며 온도의 함수라고 한다.

정력 계수는 연속적으로 더 큰 분자 그룹 간의 상호작용을 설명한다. 예를 들어, $B{\displaystyle }$ ${\displaystyle B}$은(는) 쌍 간의 상호작용을 $설명$하며,$$C {\$displaystyle$ C$}$은(는) 세 개의 가스 분자 간의 상호작용을 설명한다$$$$. 많은 수의 분자 사이의 상호작용이 드물기 때문에, 정력 방정식은 보통 3항 이후에 잘린다.^[7]

이 절단을 가정할 때 압축성 계수는 다음과 같이 분자간 힘 전위 φ에 연결된다.

${\displaystyle Z=1+2\pi {\frac {N_{\text{A}}{V_{\text{m}}\int _{0}^{\inflt }\reft(1-\exp \left)({\frac {\varphi }}{k)T}}\오른쪽)r^{2}dr}$

Real gas 기사는 압축성 인자를 계산하기 위한 더 이론적인 방법을 특징으로 한다.

온도와 압력에 의존하는 물리적 이유

압축성 인자 Z의 일탈은 매력적이고 혐오스러운 분자간 힘에 기인한다. 주어진 온도와 압력에서 반발력은 이상적인 가스를 위한 것보다 부피를 더 크게 만드는 경향이 있다; 이러한 힘이 Z를 지배할 때는 통일보다 더 크다. 매력적인 세력이 지배할 때 Z는 단결력보다 못하다. 매력적인 힘의 상대적 중요성은 온도가 증가함에 따라 감소한다(가스에 대한 효과 참조).

위에서 본 바와 같이 Z의 거동은 모든 기체에 대해 질적으로 유사하다. 분자 질소인 N은₂ 그 행동을 더 자세히 설명하고 이해하기 위해 여기서 사용된다. 이 절에 사용된 모든 데이터는 NIST 화학 웹북에서 입수했다.^[8] N의₂ 경우 액체의 정상 비등점은 77.4 K이고 임계점은 126.2 K와 34.0 bar이다.

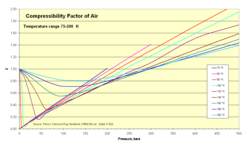
오른쪽 그림은 광범위한 온도 범위를 포괄하는 개요를 보여준다. 저온(100K)에서 곡선에는 특징적인 체크 표시 모양이 있으며, 곡선의 상승 부분은 압력에 매우 정비례한다. 중간 온도(160K)에서는 넓은 최소의 부드러운 곡선이 있다. 고압 부분이 다시 거의 선형이지만 더 이상 압력에 정비례하지 않는다. 마지막으로 고온(400K)에서 Z는 모든 압력에서 단결 이상이다. 모든 곡선에서 Z는 저압에서 단일성의 이상적인 가스 값에 접근하고 매우 높은 압력에서 그 값을 초과한다.

이러한 곡선을 더 잘 이해하기 위해 낮은 온도와 압력에 대한 동작을 두 번째 그림에서 자세히 살펴본다. 모든 곡선은 Z가 0 압력에서 일률과 같게 시작하고 Z는 압력이 증가함에 따라 처음에는 감소한다. N은₂ 이러한 조건하에서 기체여서 분자간의 거리는 크지만 압력이 증가함에 따라 작아진다. 이것은 분자 간의 매력적인 상호작용을 증가시켜 분자들을 더 가까이 끌어당기고 같은 온도와 압력에서 이상적인 기체에 비해 부피를 적게 만든다. 온도가 높을수록 매력적인 상호작용의 효과가 감소하고 기체는 거의 이상적인 방식으로 작용한다.

압력이 증가함에 따라, 가스는 결국 그림의 점선으로 보여지는 기체-액체 공존 곡선에 도달한다. 그럴 때, 매력적인 상호작용은 분자가 퍼져나가게 하는 열운동의 경향을 극복할 만큼 충분히 강해졌다; 그래서 가스는 응축되어 액체를 형성한다. 곡선의 수직 부분에 있는 점은 N이₂ 부분적으로 기체이고 부분적으로 액체인 것에 해당한다. 공존 곡선에는 Z에 대해 가능한 두 개의 값이 있는데, 이는 가스에 해당하는 큰 값과 액체에 해당하는 작은 값이다. 일단 모든 가스가 액체로 전환되면, 압력이 더 증가하면서 부피는 약간만 감소한다; 그러면 Z는 압력에 매우 비례한다.

공생곡선을 따라 온도와 압력이 높아지면 가스는 액체처럼 되고 액체는 기체처럼 된다. 결정적인 시점에서 두 사람은 같다. 따라서 임계 온도(126.2K) 이상의 온도에서는 위상 전환이 없다. 압력이 증가함에 따라 기체는 점차 액체와 같은 것으로 변한다. 임계점 바로 위에는 Z가 상당히 빠르게 떨어지는 압력 범위가 있지만(130K 곡선 참조) 높은 온도에서는 프로세스가 완전히 점진적이다.

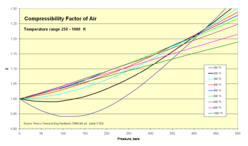
최종 수치는 임계 온도보다 훨씬 높은 온도에서의 행동을 보여준다. 혐오 상호작용은 본질적으로 온도의 영향을 받지 않지만 매력적인 상호작용은 점점 더 적은 영향을 미친다. 그러므로 충분히 높은 온도에서 반발하는 상호작용은 모든 압력에서 지배한다.

이는 고온 동작을 보여주는 그래프에서 확인할 수 있다. 온도가 증가하면 초기 기울기는 음수가 감소하고 Z가 최소인 압력은 작아지며, 혐오적 상호작용이 지배하기 시작하는 압력, 즉 Z가 단합 이하에서 단결보다 큰 것으로 변하는 압력은 작아진다. 보일 온도(N의₂ 경우 327K)에서 매력적이고 혐오스러운 효과는 낮은 압력에서 서로를 취소한다. 그 후 Z는 수십 바의 압력까지 합성의 이상적인 가스 값을 유지한다. 보일 온도 이상에서는 압축성 계수가 항상 단결보다 크고 압력이 증가함에 따라 느리지만 꾸준히 증가한다.

실험값

이상적인 기체로부터의 편차가 어떤 압력이나 온도가 중요해지는가를 일반화하기는 극히 어렵다. 경험의 법칙으로서 이상적인 가스 법칙은 약 2 atm의 압력까지 합리적으로 정확하며, 작은 비연관 분자의 경우 더욱 높다. 예를 들어 극지방 분자인 염화메틸의 경우 분자간 힘이 유의하여 압축성 인자의 실험 값은 10 atm 압력과 100 °C 온도에서$$ $Z{\displaystyle }$= $[\디스플레이$ 스타일 $Z=0.9152]$이다.^[9] 거의 동일한 조건에서 공기(작은 비극성 분자)의 경우 $압축성{\displaystyle }$ 계수는 Z${\displaystyle }$=${\displaystyle 1.0025}$ ${\디스플레이$ 스타일 $Z=1.0025}$에 불과하다($$10bar, 400K의 경우 아래 표 참조).

공기의 압축성

정상 공기는 80퍼센트의 질소 N과
₂ 20퍼센트의 산소 O로
₂ 구성된다. 두 분자는 모두 작고 극성이 아니다(따라서 연관성이 없다). 그러므로 우리는 넓은 온도 및 압력 범위 내에서 공기의 행동을 합리적인 정확도를 가진 이상적인 기체로 근사하게 추정할 수 있다고 기대할 수 있다. 압축성 인자에 대한 실험 값은 이를 검증한다.

• 압력 1~500bar의 함수로서 공기에 대한 Z
• 

  75–200 K 등축

• 

  250–1000 K 등축

공기의 압축성 계수(실험적 값)^[10]

온도(K)	압력, 절대(막대)
	1	5	10	20	40	60	80	100	150	200	250	300	400	500
75	0.0052	0.0260	0.0519	0.1036	0.2063	0.3082	0.4094	0.5099	0.7581	1.0125
80		0.0250	0.0499	0.0995	0.1981	0.2958	0.3927	0.4887	0.7258	0.9588	1.1931	1.4139
90	0.9764	0.0236	0.0453	0.0940	0.1866	0.2781	0.3686	0.4681	0.6779	0.8929	1.1098	1.3110	1.7161	2.1105
100	0.9797	0.8872	0.0453	0.0900	0.1782	0.2635	0.3498	0.4337	0.6386	0.8377	1.0395	1.2227	1.5937	1.9536
120	0.9880	0.9373	0.8860	0.6730	0.1778	0.2557	0.3371	0.4132	0.5964	0.7720	0.9530	1.1076	1.5091	1.7366
140	0.9927	0.9614	0.9205	0.8297	0.5856	0.3313	0.3737	0.4340	0.5909	0.7699	0.9114	1.0393	1.3202	1.5903
160	0.9951	0.9748	0.9489	0.8954	0.7803	0.6603	0.5696	0.5489	0.6340	0.7564	0.8840	1.0105	1.2585	1.4970
180	0.9967	0.9832	0.9660	0.9314	0.8625	0.7977	0.7432	0.7084	0.7180	0.7986	0.9000	1.0068	1.2232	1.4361
200	0.9978	0.9886	0.9767	0.9539	0.9100	0.8701	0.8374	0.8142	0.8061	0.8549	0.9311	1.0185	1.2054	1.3944
250	0.9992	0.9957	0.9911	0.9822	0.9671	0.9549	0.9463	0.9411	0.9450	0.9713	1.0152	1.0702	1.1990	1.3392
300	0.9999	0.9987	0.9974	0.9950	0.9917	0.9901	0.9903	0.9930	1.0074	1.0326	1.0669	1.1089	1.2073	1.3163
350	1.0000	1.0002	1.0004	1.0014	1.0038	1.0075	1.0121	1.0183	1.0377	1.0635	1.0947	1.1303	1.2116	1.3015
400	1.0002	1.0012	1.0025	1.0046	1.0100	1.0159	1.0229	1.0312	1.0533	1.0795	1.1087	1.1411	1.2117	1.2890
450	1.0003	1.0016	1.0034	1.0063	1.0133	1.0210	1.0287	1.0374	1.0614	1.0913	1.1183	1.1463	1.2090	1.2778
500	1.0003	1.0020	1.0034	1.0074	1.0151	1.0234	1.0323	1.0410	1.0650	1.0913	1.1183	1.1463	1.2051	1.2667
600	1.0004	1.0022	1.0039	1.0081	1.0164	1.0253	1.0340	1.0434	1.0678	1.0920	1.1172	1.1427	1.1947	1.2475
800	1.0004	1.0020	1.0038	1.0077	1.0157	1.0240	1.0321	1.0408	1.0621	1.0844	1.1061	1.1283	1.1720	1.2150
1000	1.0004	1.0018	1.0037	1.0068	1.0142	1.0215	1.0290	1.0365	1.0556	1.0744	1.0948	1.1131	1.1515	1.1889

${\displaystyle Z}$ ${\displaystyle Z}$ 값은$$ 바세르만, 카자브친스키, 라비노비치에서 압력, 부피(또는 밀도) 및 온도의 값, "공기 및 공기 구성요소의 열물리학적 특성; 모스크바, 나우카, 1966 및 NBS-NSF 트랜스'에서 계산된다. TT 70-50095, 1971: 및 바세르만과 라비노비치 "액체 공기와 그 구성요소의 열물리학적 특성 "모스코우, 1968 및 NBS-NSF Transs. 69-55092, 1970.

참고 항목

• 도망성
• 리얼 가스
• 해당 상태의 정리
• 반데르발스 방정식

참조

외부 링크

• 압축성 인자(가제) ACitizendium 기사.
• 실제 가스는 압축성 요인에 대한 논의를 포함한다.