유한충동반응

신호 처리에서 유한 임펄스 응답(FIR) 필터는 유한한 시간에 0으로 안착하기 때문에 임펄스 응답(또는 유한한 길이 입력에 대한 응답)이 유한한 지속시간인 필터다. 이는 무한충동반응(IIIR) 필터와는 대조적인 것으로, 내부 피드백이 있을 수 있고 무한정 반응(보통 붕괴)할 수 있다.

N-오더^th 이산 시간 FIR 필터의 임펄스 응답(즉, 크론커 델타 입력에 대한 응답 출력)은 정확히 $N+1$ + 1 ${\displaystyle$ N $+1}$ 샘플 $N+1$ (첫 번째 0이 아닌 원소에서 마지막 0이 아닌 원소까지)이 0으로 설정되기 전에 지속된다.

FIR 필터는 이산 시간 또는 연속 시간, 디지털 또는 아날로그일 수 있다.

정의

순서 N의 직접 형태 이산 시간 FIR 필터. 상단부는 N+1탭이 있는 N단계 지연선이다. 각 단위 지연은 Z 변환 표기법으로 z 연산자다⁻¹.

순서 N의 격자형 이산 시간 FIR 필터. 각 단위 지연은 Z 변환 표기법으로 z 연산자다⁻¹.

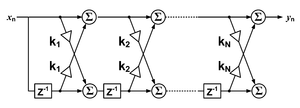
순서 N의 원인 이산 시간 FIR 필터의 경우, 출력 시퀀스의 각 값은 가장 최근의 입력 값의 가중 합이다.

{\begin}y[n]&=b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{N}x[n-N]\&=\sum _{i=0}^{N}b_{n-i}}}cdot x[n-i],\ended}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

여기서:

${\textstyle x[n]}$ [ ${\textstyle x[n]}$ ${\textstyle x[n]}$ ${\textstyle x[n]}$ 은 ${\textstyle x[n]}$ (는) 입력 신호,
${\textstyle y[n]}$ [ ${\textstyle y[n]}$ ${\textstyle y[n]}$ ${\textstyle y[n]}$ 은 ${\textstyle y[n]}$ (는) 출력 신호,
${\textstyle N}$ ${\textstyle N}$ 이 ${\textstyle N}$ (가) 필터 순서임. ${\textstyle N}$ {\ $textstyle$ N $}-$ order ${\textstyle N}$ ^th 필터 오른쪽에는 ${\textstyle N+1}$ + 1 ${\textstyle$ N+1} $개의$ 항이 ${\textstyle N+1}$ 있음
${\textstyle b_{i}}$ ${\textstyle b_{i}}$ ${\$ 은(는) ${\textstyle N^{\text{th}}}$ ${\textstyle N^{\text{th}}}$ ${\$ N $^{\text{th}$ -Order ${\textstyle N^{\text{th}}}$ FIR ${\textstyle 0\leq i\leq N}$ $필터$ 의 0 ${\textstyle 0\leq i\leq N}$ i ${\$ }에 대한 I'번째 순간의 임펄스 응답 값이다 ${\textstyle b_{i}}$ . 필터가 직접 형태 FIR 필터인 경우 ${\textstyle b_{i}}$ i ${\$ 도 필터 계수다 ${\textstyle b_{i}}$ .

이 계산은 이산 콘볼루션으로도 알려져 있다.

이러한 용어의 ${\textstyle x[n-i]}$ ${\textstyle x[n-i]}$ [ n ${\textstyle x[n-i]}$ - ${\textstyle x[n-i]}$ ${\textstyle x[n-i]}$ ${\textstyle x[n-i]}$ 은(는) 많은 구현 또는 블록 다이어그램에서 곱셈 작업에 지연된 입력을 제공하는 탭의 구조에 기초하여 일반적으로 taps라고 불린다. 예를 들어, 5번째 순서/6번째 탭 필터에 대해 말할 수 있다.

정의된 필터의 임펄스 응답은 유한한 지속시간에 걸쳐 0이 아니다. 0을 포함하여, 충동 반응은 무한 시퀀스:

h[n]=\sum _{i=0}^{{N}b_{i}\cdot \delta [n-i]={\begin}b_{n}\leq N\0&{n\leq n\n&{otherwise}.\end{case}}

FIR 필터가 비-주의적인 경우, 충격 반응에서 0이 아닌 값의 범위는 정의 공식이 적절하게 일반화된 $n=0$ 에서 n $n=0$ = $n=0$ ${\displaystyle n=0$ 이전에 시작할 수 있다.

특성.

FIR 필터는 때로는 무한충동 응답(IIIR) 필터보다 선호되는 많은 유용한 속성을 가지고 있다. FIR 필터:

피드백을 요구하지 않는다. 즉, 반올림 오류는 총 반복으로 복합되지 않는다. 각 계산에서 동일한 상대적 오류가 발생한다. 이것은 또한 구현을 더 단순화시킨다.
출력은 입력값의 유한한 배수의 합이므로 입력에 나타나는 가장 큰 값의 ${\textstyle \sum |b_{i}|}$ ${\textstyle \sum |b_{i}|}$ i $textstyle \sum b_{i}$ 보다 ${\textstyle \sum |b_{i}|}$ 클 수 없기 때문에 본질적으로 안정적이다.
계수 시퀀스를 대칭으로 만들어 선형 위상이 되도록 쉽게 설계할 수 있다. 이 속성은 데이터 통신, 지진학, 교차 필터 및 마스터링과 같은 위상 민감 애플리케이션에 필요할 때도 있다.

FIR 필터의 주요 단점은 특히 저주파(샘플 속도에 상대적인) 컷오프가 필요한 경우, 유사한 선명도 또는 선택성을 가진 IIR 필터에 비해 범용 프로세서의 연산력이 상당히 더 많이 필요하다는 것이다. 그러나 많은 디지털 신호 프로세서는 FIR 필터를 많은 애플리케이션에서 IIR만큼 대략적으로 효율적이게 만들기 위해 전문화된 하드웨어 기능을 제공한다.

주파수 응답

필터의 시퀀스 $x[n]$ [ $x[n]$ $x[n]$ $x[n]$ 에 대한 영향은 콘볼루션 정리에 의해 주파수 영역에 설명된다 $x[n]$ .

\underbrace {{\mathcal {F}}\{x*h\}} _{Y(\omega )}=\underbrace {{\mathcal {F}}\{x\}} _{X(\omega )}\cdot \underbrace {{\mathcal {F}}\{h\}} _{H(\omega )}

and

y[n]=x[n]*h[n]={\mathcal {F}}^{-1}{\big \{}X(\omega )\cdot H(\omega ){\big \}},

{\displaystyle y[n]=x[n]*h[n]={\mathcal{F}^{1}{\big \}X(\omega )\cdot

여기서 연산자 ${\mathcal {F}}$ ${\$ 과 ${\mathcal {F}}$ ( ${\mathcal {F}}^{-1}$ F ${\mathcal {F}}^{-1}$ - 1 {\ $displaystyle$ {\ $mathcal$ { $F}^{-1}$ 는 ${\mathcal {F}}^{-1}$ 각각 이산 시간 푸리에 변환(DTFT)과 그 역순을 나타낸다. 따라서 복합 값 $H(\omega )$ 함수 H( $H(\omega )$ ) $displaystyle$ H $(\omega )}$ 은 필터의 주파수 응답이다 $H(\omega)$ . Fourier 시리즈로 정의된다.

H_{2\pi }(\omega )\ \triangleq \sum _{n=-\infty }^{\infty }h[n]\cdot \left({e^{i\omega }}\right)^{-n}=\sum _{n=0}^{N}b_{n}\cdot \left({e^{i\omega }}\right)^{-n},

여기서 첨자가 추가된 것은 2개의 첨자성을 나타낸다. 여기서 $\omega$ $\omega$ 은 $\omega$ (는) 정규화된 단위로 주파수를 나타낸다(라디안/샘플). 대체 $\omega =2\pi f,$ = $\omega =2\pi f,$ $\omega =2\pi f,$ f , $\omega =2\pi f,$ {\ $displaystyle \omega =2\pi$ f $,}$ 많은 필터 설계 프로그램에서 선호하는 $\omega =2\pi f,$ 주파수(^[A] $(f)$ ) ${\displaystyle$ (f $)$ 의 단위를 주기/샘플로 $(f)$ 변경하고 주기성을 1로 변경한다. x[n] 시퀀스에 알려진 샘플링 $f_{s}$ 인 f $f_{s}$ {\ $displaystyle f_{s}$ 샘플 $f_{s}$ /second가 있는 경우, $\omega =2\pi f/f_{s}$ $\omega =2\pi f/f_{s}$ = 2 $\omega =2\pi f/f_{s}$ f $\omega =2\pi f/f_{s}$ / $\omega =2\pi f/f_{s}$ $s$ ${\$ $displaystyle \$ $omega=2\pi f/f_s$ $}}$ 의 주파수 $(f)$ 단위를 주기/초 $($ 헤르츠 $(f)$ 로 $(f)$ 변경하고 $\omega =2\pi f/f_{s}$ 주기성을 $.$ {\ $displaystylease f_f_s}$ . $}}$ $\omega =\pi$ = $\omega =\pi$ $\omega =\pi$ 은 $f_s.$ $f={\tfrac {f_{s}}{2}}$ 는) f = f 2 $f={\tfrac {f_{s}}{2}}$ {\ $displaystyle$ f $={f_{s}}{2$ }} $f={\tfrac {f_{s}}{2}}$ Hz $f={\tfrac {f_{s}}{2}}$ $={\tfrac {1}{2}}$ = $={\tfrac {1}{2}}$ $={\tfrac {1}{2}}$ ${\$ 의 $= \tfrac{1}{2}$ 주기/샘플에 해당한다 $\omega =\pi$ .

$H_{2\pi }(\omega )$ $H_{2\pi }(\omega )$ $H_{2\pi }(\omega )$ ( $H_{2\pi }(\omega )$ ) $H_{2\pi }}(\omega )$ 도 필터 임펄스 응답의 Z 변환의 관점에서 표현할 수 있다 $H_{2\pi }(\omega )$ .

{\widehat{H}(z)\ \triangleq \sum _{n=-\nft }^{\nflt }h[n]\cdot z^{-n}.

H_{2\pi }(\omega )=\왼쪽.{\widehat{H}(z)\,\right _{z=e^{j\omega}}={\widehat{H}(e^{j\omega }).

필터 디자인

FIR 필터는 시간 영역(예: 일치된 필터) 및/또는 주파수 영역(가장 일반적인 필터)에 있을 수 있는 특정 사양을 충족하는 계수 및 필터 순서를 찾아 설계한다. 일치하는 필터는 입력 신호와 알려진 펄스 모양 사이의 교차 상관 관계를 수행한다. FIR convolution은 입력 신호와 임펄스 응답의 시간 역반복 사본 사이의 교차 상관관계다. 따라서 일치하는 필터의 임펄스 응답은 알려진 펄스 형태를 샘플링하여 필터 계수로 역순으로 사용하여 "설계"된다.^[1]

특정 주파수 응답을 원하는 경우 다음과 같은 몇 가지 다른 설계 방법이 일반적이다.

창구설계법
주파수 샘플방식
최소 MSE(평균 제곱 오차) 방법
Parks-McClellan 방법(Equiriple, Optimal 또는 Minimax 방법으로도 알려져 있다). 레메즈 교환 알고리즘은 최적 등분계수 집합을 찾는 데 일반적으로 사용된다. 여기서 사용자는 원하는 주파수 응답, 이 응답의 오류에 대한 가중 함수, 필터 순서 N을 지정한다. 그런 다음 알고리즘은 이상과의 최대 편차를 최소화하는 ${\textstyle N+1}$ + ${\textstyle N+1}$ ${\textstyle N+1}$ 계수 ${\textstyle N+1}$ 집합을 찾는다. 직관적으로 ${\textstyle N+1}$ + ${\textstyle N+1}$ ${\textstyle N+1}$ 계수만 ${\textstyle N+1}$ 사용할 수 있는 경우 원하는 응답에 최대한 가까운 필터를 찾는다. 이 방법은 적어도 하나의 텍스트가^[2] 원하는 필터와 N을 사용하고 최적 계수를 반환하는 프로그램을 포함하기 때문에 특히 실무에서 쉽다.
Equiripple FIR 필터도 DFT 알고리즘을 사용하여 설계할 수 있다.^[3] 그 알고리즘은 본질적으로 반복적이다. 초기 필터 설계의 DFT는 FFT 알고리즘을 사용하여 계산된다(초기 견적을 사용할 수 없는 경우 h[n]=delta[n]를 사용할 수 있다). Fourier 도메인, 즉 DFT 도메인에서, 주파수 응답은 원하는 사양에 따라 수정되며, 그 후 역 DFT가 계산된다. 시간 영역에서는 첫 번째 N 계수만 유지된다(다른 계수는 0으로 설정됨). 그런 다음 프로세스는 반복적으로 반복된다: DFT는 다시 한번 계산되고, 주파수 영역에는 보정이 적용된다.

MATLAB, GNU 옥타브, Scilab, SciPy와 같은 소프트웨어 패키지는 이러한 다양한 방법을 적용할 수 있는 편리한 방법을 제공한다.

창구설계법

창 설계 방법에서는 우선 이상적인 IIR 필터를 설계한 다음, 유한 길이 창 함수에 곱하여 무한 임펄스 반응을 잘라낸다. 그 결과는 IIR 필터로부터 주파수 응답이 수정된 유한 임펄스 응답 필터다. 시간영역에서 윈도우 기능에 의한 무한충동을 곱하면 IIR의 주파수 응답은 윈도우 기능의 푸리에 변환(또는 DTFT)으로 수렴된다. 윈도우의 주엽이 좁은 경우 복합 주파수 응답은 이상적인 IIR 필터에 가깝게 유지된다.

이상적인 반응은 종종 직사각형이며, 해당 IIR은 sinc 함수다. 주파수 영역 콘볼루션의 결과는 사각형의 가장자리가 테이퍼로 되어 있고, 통과 대역과 정지 대역에 잔물결이 나타난다. 역방향으로 작업하면 테이퍼 영역(변환 밴드)의 기울기(또는 너비)와 리플의 높이를 지정해 적절한 창 기능의 주파수 영역 파라미터를 도출할 수 있다. 임펄스 응답으로 역행하는 것은 필터 설계 프로그램을 반복하여 최소 필터 순서를 찾아냄으로써 이루어질 수 있다. 또 다른 방법은 솔루션 세트를 Kaiser 창의 파라메트릭 계열로 제한하여 시간 영역과 주파수 영역 매개변수 사이의 폐쇄적인 형태 관계를 제공하는 것이다. 일반적으로 이 방법은 가능한 최소한의 필터 순서를 달성하지는 못하지만, 동적이고 즉각적인 필터 설계를 필요로 하는 자동화된 애플리케이션에 특히 편리하다.

윈도우 설계 방법은 다른 샘플 포인트(중앙 1 제외)마다 해당 sinc 함수가 0이기 때문에 효율적인 하프밴드 필터를 만드는 데도 유리하다. 윈도우 기능이 있는 제품은 0을 변경하지 않기 때문에 최종 임펄스 반응 계수의 거의 절반은 0이다. FIR 계산의 적절한 구현은 필터의 효율성을 배가시키기 위해 그 속성을 이용할 수 있다.

최소 평균 제곱 오차(MSE) 방법

목표:

MSE 감각으로 FIR 필터를 설계하기 위해 얻은 필터와 원하는 필터 사이의 평균 제곱 오차를 최소화한다.

{\displaystyle {\text{M

SE}}=f_{s}^{-1}\int _{-f_{s}/2}^{f_{s}/2} H(f)-H_{d}(f) ^{2}\,df}

, where

f_{s}\,

is sampling frequency,

H(f)\,

is the spectrum of the filter we obtained, and

H_{d}(f)\,

is the spectrum of the desired filter.

방법:

N-point

h[n]

필터 h

h[n]

[

h[n]

h[n]

h[n]

및 r

r[n]=h[n+k],k={\frac {(N-1)}{2}}

[

r[n]=h[n+k],k={\frac {(N-1)}{2}}

=

r[n]=h[n+k],k={\frac {(N-1)}{2}}

[

r[n]=h[n+k],k={\frac {(N-1)}{2}}

n +

r[n]=h[n+k],k={\frac {(N-1)}{2}}

= (

r[n]=h[n+k],k={\frac {(N-1)}{2}}

-

r[n]=h[n+k],k={\frac {(N-1)}{2}}

) 2

{\

1단계:

h[n]

[

h[n]

h[n]

h[n]

이

h[n]

(가) 대칭이라고 가정합시다. 그런 다음

r[n]

[

r[n]

]

r[n]

의 이산 시간 푸리에 변환을 다음과 같이 정의한다

r[n]

.

R(F)=e^{j2\pi Fk}H(F)=\sum _{n=0}^{k}s[n]\cos(2\pi nF)

2단계: 평균 제곱 오차를 계산하십시오.

{\text{MSE}}=\int _{-1/2}} R(F)-H_{d}(F) ^{2}\,dF

그러므로

{\text{MSE}}=\int _{-1/2}^{1/2}\sum _{n=0}^{k}s[n]\cos(2\pi nF)\sum _{\tau =0}^{k}s[\tau ]\cos(2\pi \tau F)\,dF-2\int _{-1/2}^{1/2}\sum _{n=0}^{k}s[n]\cos(2\pi nF)H_{d}\,dF+\int _{-1/2}^{1/2}H_{d}(F)^{2}\,dF

3단계:

s[n]

[

s[n]

s[n]

s[n]

과(와) 관련하여 MSE의 부분파생물을 수행하여 평균 제곱 오차를 최소화하십시오.

{\frac {\partial {\text{M}SE}}{\partial s[n]}=2\sum _{\tau =0}^{k}s[\tau ]\int _{-1/2}^{1/2}\cos(2\pi nF)\cos(2\pi-2\int)\,dF-2\int _{1/2}}H_{d}(F)^{2}\cos(2\pi nF)\,dF=0

조직화된 후, 우리는

s[0]=\int _{-1/2}^{1/2}H_{d}(F)\,dF

{\displaystyle s[n]=\int _{-1/2}^{1/2}\cos(2\pi nF)H_{d}(F)\,dF,\{\text{{}의 경우.

4단계:

s[n]

[

s[n]

s[n]

s[n]

을(를)

h[n]

[

h[n]

h[n]

h[n]

의 프레젠테이션으로 되돌리십시오

s[n]

.

H[k])s[0], h[k+n])s[n]/2, h[k− n])s[n]/2, f마다 rn=1,2,3,…, k, k=(N1−)/2{\displaystyle h[k]=s[0],h[k+n]=s[n][k-n]=s[n]/2,\, for\, n=1,2,3,\ldots ,k,{\text{어디}}k=(N-1)/2}와 엔<>에 h[n]=0;0과 n≥ N{\displaystyle h[n]=0{\text{에}}n<0{\tex.t{

및 }}n\geq N}

또한 가중 $W(f)$ W $W(f)$ f $W(f)$ ){\ $displaystyle W($ f)}를 추가하여 필요에 따라 패스밴드 및 스톱밴드의 중요성을 다르게 취급할 수 있다. 그러면 $W(f)$ MSE 오류가 발생하게 된다.

{\text{MSE}}=\int _{-1/2}}W(F) R(F)-H_{d}(F) ^{2}\,dF

이동 평균 예제

단순 FIR 필터의 블록 다이어그램(이 경우 2차/3탭 필터, 이동 평균 평활 필터 구현)

2차 FIR 스무딩 필터의 폴-제로 다이어그램

2차 FIR 평활 필터의 크기 및 위상 반응

2차 FIR 평활 필터의 예시 진폭 및 위상 반응

이동 평균 필터는 매우 간단한 FIR 필터다. 때로는 박스카 필터라고 부르기도 하는데, 특히 소멸이 뒤따를 때는 더욱 그렇다. 필터 계수 b ${\textstyle b_{0},\ldots ,b_{N}}$ , ${\textstyle b_{0},\ldots ,b_{N}}$ … , ${\textstyle b_{0},\ldots ,b_{N}}$ ${\textstyle b_{0},\ldots ,b_{N}}$ ${\$ 은 ${\textstyle b_{0},\ldots ,b_{N}}$ 는) 다음 방정식을 통해 확인할 수 있다.

b_{i}={\frac {1}{N+1}

보다 구체적인 예를 제공하기 위해 필터 순서를 선택하십시오.

N=2

결과 필터의 임펄스 응답은 다음과 같다.

h[n]={\frac {1}{1}{3}\messages [n]+{\frac {1}{1}}\messages [n-2]}

오른쪽의 블록 다이어그램은 아래에서 설명하는 2차 이동 평균 필터를 보여준다. 전송 기능은 다음과 같다.

H(z)={\frac {1}{1}{3}}+{\frac{1}{1}{3}}+{1}{3}z^{1}{3}={\frac {1}{1}}{3}}{\frac {z^{2}+1}{z^1}:{2}}.

다음 그림은 해당하는 극-제로 도표를 보여준다. 0 주파수(DC)는 (1, 0)에 해당하며, (-1, 0)에서 니키스트 주파수로 원을 중심으로 시계 반대 방향으로 전진하는 양의 주파수. Two poles are located at the origin, and two zeros are located at ${\textstyle z_{1}=-{\frac {1}{2}}+j{\frac {\sqrt {3}}{2}}}$ , ${\textstyle z_{2}=-{\frac {1}{2}}-j{\frac {\sqrt {3}}{2}}}$ .

주파수 응답(표준화된 주파수 Ω)은 다음과 같다.

{\reasoned}H\left(e^{j\omega }\right)&={\frac {1}{3}}+{\frac {1}{3}}e^{-j\omega }+{\frac {1}{3}}e^{-j2\omega }\\&={\frac {1}{3}}e^{-j\omega }\left(1+2\cos(\omega )\right).\end{정렬}}

그림에는 ${\textstyle H\left(e^{j\omega }\right)}$ ${\textstyle H\left(e^{j\omega }\right)}$ ${\textstyle H\left(e^{j\omega }\right)}$ ${\textstyle H\left(e^{j\omega }\right)}$ ) ${\$ 의 크기와 위상 성분이 표시된다. 그러나 이와 같은 플롯은 임펄스 반응의 이산 푸리에 변환(DFT)을 수행함으로써 생성될 수도 있다.^[B] 그리고 대칭성 때문에 필터 설계나 보기 소프트웨어는 종종 [0, ]] 영역만 표시한다. 크기 그림은 이동 평균 필터가 1에 가까운 이득으로 낮은 주파수를 통과하여 높은 주파수를 감쇠시키므로 조잡한 저역 통과 필터임을 나타낸다. 위상 그림은 크기가 0이 되는 두 주파수에서 불연속성을 제외하고 선형이다. 불연속부의 크기는 π이며, 부호반전을 나타낸다. 최종 그림에서와 같이 선형 위상의 속성에 영향을 주지 않는다.

참고 항목

메모들

^ 예외적으로 MATLAB는 반주기/표본 = 주기/2-표본의 단위를 선호하는데, 그 단위의 나이키스트 주파수가 1이기 때문에, 0에서 나이키스트 주파수까지의 간격을 표시하는 소프트웨어를 플로팅하는 데 편리한 선택이다.
^ § DTFT 샘플링을 참조하십시오.

참조

^ 오펜하임, 앨런 V, 윌스키, 앨런 S, 영, 이안 T, 1983: 신호와 시스템, 페이지 256 (뉴저지 주 잉글우드 클리프스: 프렌티스 홀, Inc.) ISBN 0-13-809731-3
^ 라비너, 로렌스 R, 그리고 골드, 버나드 1975: 디지털 신호 처리 이론과 응용 (Englewood Cliffs, New Jersey: Fratice-Hall, Inc.) ISBN 0-13-914101-4
^ A. E. Cetin, O.N. Gerek, Y. Jadimci, "FFT 알고리즘에 의한 Equiripple FIR 필터 설계," IEEE 신호 처리 잡지 페이지 60–64, 1997년 3월.

[1] 예외적으로 MATLAB는 반주기/표본 = 주기/2-표본의 단위를 선호하는데, 그 단위의 나이키스트 주파수가 1이기 때문에, 0에서 나이키스트 주파수까지의 간격을 표시하는 소프트웨어를 플로팅하는 데 편리한 선택이다.

[5] § DTFT 샘플링을 참조하십시오.

[2] 오펜하임, 앨런 V, 윌스키, 앨런 S, 영, 이안 T, 1983: 신호와 시스템, 페이지 256 (뉴저지 주 잉글우드 클리프스: 프렌티스 홀, Inc.) ISBN 0-13-809731-3

[3] 라비너, 로렌스 R, 그리고 골드, 버나드 1975: 디지털 신호 처리 이론과 응용 (Englewood Cliffs, New Jersey: Fratice-Hall, Inc.) ISBN 0-13-914101-4

[4] A. E. Cetin, O.N. Gerek, Y. Jadimci, "FFT 알고리즘에 의한 Equiripple FIR 필터 설계," IEEE 신호 처리 잡지 페이지 60–64, 1997년 3월.

[A]

[1]

[2]

[3]

[B]

Search