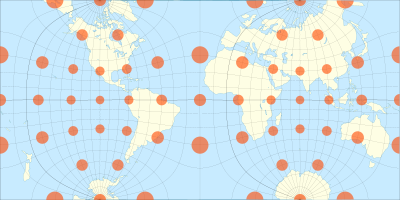
구유 반구 정사각형 투영법
Guyou hemisphere-in-a-square projection구유 반구형 투영법은 반구를 위한 정합 지도 투영법이다. 그것은 Peirce Quincurnic 투영의 비스듬한 측면이다.
역사
이 투영은 1887년 프랑스의 에밀 구유에 의해 개발되었다.[1] [2]
형식 설명
투영은 축을 45도 회전시켜 Peirce Quincitical 투영의 비스듬한 측면으로 계산할 수 있다. 또한 입체 투영을 계산하기 전에 좌표 -45도를 회전하여 계산할 수도 있다. 그런 다음 이 투영은 좌표가 45도 회전되는 정사각형으로 다시 연결된다.[3]
투영은 각 반구 사각형의 네 모서리를 제외하고 일치한다. 다른 정합 다각형 투영과 마찬가지로 구유는 슈바르츠-크리스토펠 지도화다.
특성.
그것의 특성은 Peirce Quincital의 특성과 매우 유사하다.
- 각 반구는 정사각형으로, 구는 종횡비 2:1의 직사각형으로 표현된다.
- 각 정사각형의 중앙에서 구면적의 9%에 불과하며, 메르카토르 13%, 스테레오 50[4]%에 비해 스케일의 과장이 2배에 달하는 부분은 구면적의 9%에 불과하다.
- 큰 원을 나타내는 선의 곡률은 모든 경우 길이의 큰 부분에 걸쳐 매우 미미하다.[4]
- 그것은 각 반구에 해당하는 사각형의 모서리를 제외하고 어디에서나 일치하며, 두 개의 경맥이 각각 두 번씩 갑자기 방향을 바꾼다; 적도는 수평선으로 표현된다.
- 그것은 모든 방향으로 테셀링될 수 있다.
관련 투영
- 아담스 반구-a-제곱 투영과 Peirce Quincial 투영은 동일한 기초의 슈바르츠-크리스토펠 매핑의 다른 측면이다. 그러한 매핑은 절반의 입체 투영의 변형이다.
참고 항목
참조
- ^ E. Guyo (1887) "Nouveau systéme de la spherer: Généralization de la projection de Mercator", Annales hydrogrique, Ser 2, Vol. 9, 16–35. https://www.retronews.fr/journal/annales-hydrographiques/1-janvier-1887/1877/4868382/23
- ^ Snyder, John P. (1993). Flattening the Earth. University of Chicago. ISBN 0-226-76746-9.
- ^ L.P. Lee (1976). "Conformal Projections based on Elliptic Functions". Cartographica. 13 (Monograph 16, supplement No. 1 to Canadian Cartographer).
- ^ Jump up to: a b C.S. Peirce (December 1879). "A Quincuncial Projection of the Sphere". American Journal of Mathematics. The Johns Hopkins University Press. 2 (4): 394–396. doi:10.2307/2369491. JSTOR 2369491.