해시 테이블

해시 테이블
해시 테이블
유형	순서 없는 연관 배열
발명된	1953
빅 O 표기의 시간 복잡도
알고리즘.
알고리즘.
공간
서치
삽입
삭제

해시 테이블로서의 작은 전화번호부

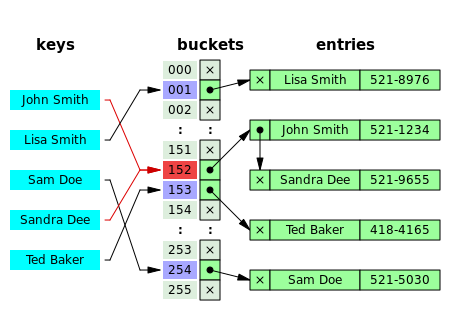
컴퓨팅에서 해시 맵 또는 사전으로도 알려진 해시 테이블은 키에 값을 매핑할 수 있는 구조인 집합 추상 데이터 유형을 구현하는 데이터 구조입니다.해시 테이블은 해시 함수를 사용하여 원하는 값을 찾을 수 있는 버킷 또는 슬롯 배열로 인덱스를 계산합니다.조회 중에 키가 해시되고 결과 해시는 대응하는 값이 저장되어 있는 위치를 나타냅니다.

해시 함수는 각 키를 하나의 버킷에 할당하는 것이 이상적이지만 대부분의 해시 테이블 설계에서는 불완전한 해시 함수를 사용합니다.이 때문에 해시 함수가 여러 키에 대해 동일한 인덱스를 생성하는 해시 충돌이 발생할 수 있습니다.그러한 충돌은 일반적으로 어떤 식으로든 수용된다.

고차원 해시 테이블에서 각 룩업의 평균 시간 복잡도는 테이블에 저장되어 있는 요소의 수에 의존하지 않는다.또한 많은 해시 테이블 설계에서는 키-값 쌍을 상각된 ^[2]^[3]^[4]작업당 일정한 평균 비용으로 임의로 삽입 및 삭제할 수 있습니다.

해시는 시공간의 트레이드오프의 한 예입니다.메모리가 무한대인 경우 키 전체를 인덱스로 직접 사용하여 단일 메모리 액세스로 값을 찾을 수 있습니다.한편, 무한대의 시간을 사용할 수 있는 경우는, 키에 관계없이 값을 보존할 수 있어 바이너리 검색이나 선형 검색을 사용해 ^[5]^{: 458}요소를 검색할 수 있습니다.

대부분의 경우 해시 테이블은 검색 트리나 다른 테이블 검색 구조보다 평균적으로 더 효율적입니다.이러한 이유로 특히 연관 배열, 데이터베이스 인덱싱, 캐시 및 세트 등 다양한 종류의 컴퓨터 소프트웨어에 널리 사용됩니다.

역사

해시에 대한 생각은 다른 장소에서 독립적으로 일어났다.1953년 1월, Hans Peter Luhn은 체인과 해싱을 사용하는 IBM 내부 메모를 작성했습니다.오픈 어드레싱은 나중에 Luhn의 논문에서 A.^[6]^{: 15} D. Linh 빌딩에 의해 제안되었다.비슷한 시기에 IBM Research의 Gene Amdahl, Elaine M. McGraw, Nathaniel Rochester 및 Arthur Samuel은 IBM 701 어셈블러를 ^[7]^{: 124}위해 해시를 구현했습니다.선형 프로브를 사용한 오픈 어드레싱은 Amdahl에 의한 것으로 인정되지만, Ershov는 독립적으로 같은 생각을 ^[7]^{: 124–125}가지고 있었습니다."오픈 어드레싱"이라는 용어는 W에 의해 만들어졌습니다. Wesley Peterson은 큰 ^[6]^{: 15}파일 검색의 문제를 논하는 그의 기사에 있습니다.

체인을 이용한 해시에 관한 첫 번째 연구는 나머지 모듈 프라임을 해시 ^[6]^{: 15}함수로 사용하는 아이디어를 논의한 Arnold Dumey의 공로를 인정받았다.해싱이라는 단어는 로버트 ^[7]^{: 126}모리스의 기사에 의해 처음 출판되었다.선형 탐침의 이론적 분석은 원래 Konheim과 ^[6]^{: 15}Weiss에 의해 제출되었습니다.

개요

해시 테이블은 n $=$ 요소의 집합 S(\ $displaystyle S)$ 를 $S$ m $(\displaystyle$ m $m$ $m$ 의 연관 $배열$ A(\ $displaystyle$ A $)$ 에 $A$ 저장하는 데 사용되는 집합 $추상$ 데이터 유형의 구현입니다. $m\geq n$ 서 m $(\displaystyle$ m $\geq$ n $m\geq n$ 은 $n=|S|$ 시간이 더 복잡합니다.자체 밸런싱 바이너리 검색 ^[6]^{: 1}트리와 비교하여 검색, 삭제 및 삽입 작업을 수행합니다. $값$ x $(\displaystyle$ x $)$ 는 $x$ 인덱스 $A[h(x)]$ A [ $A[h(x)]$ ( $A[h(x)]$ x $)\displaystyle$ A [h $(x$ 에 저장됩니다. $h$ 서h(\ $displaystyle$ h $)$ 는 $h$ 해시 함수이며 h $h(x)<m$ < $(x$ ) < $displaystyle$ h( $x)$ < $m$ ^[6]^{: 2} 입니다.

부하율

$(\displaystyle \alpha)$ 는 $\alpha$ 해시 테이블의 중요한 통계량이며 ^[1]다음과 같이 정의됩니다.

(\displaystyle {text{load factor}}\(\alpha)=syslogfrac {n}{k}})

어디에

$\displaystyle$ n은 $n$ 해시 테이블에서 사용되는 엔트리의 수입니다.
$\displaystyle$ k는 버킷의 $k$ 수입니다.

해시테이블의 성능은 $(\displaystyle\alpha$ ^[6]^{: 2}에 비해 저하되므로 $(\displaystyle\alpha)$ 가 $\alpha$ ^[8]1에 가까워지면 해시테이블의 크기가 조정되거나 재탕됩니다.부하계수가 $\alpha _{\max }/4$ max / $(\displaystyle \alpha$ _ ${\max$ $\alpha$ }/ $4$ ^[8] $\alpha _{\max }/4$ 으로 떨어졌을 경우에도 테이블 크기가 변경됩니다. $\alpha$ α(\ $displaystyle$ \alpha $\alpha$ })의 $\alpha$ 허용 가능한 수치에는 0.6과 0.^[9]^[10]^{: 110}75가 포함됩니다.

해시함수

$h:U\rightarrow \{0,...,m-1\}$ $함수$ h(\ $displaystyle$ h $)$ 는 $h$ $U$ $키$ h $h:U\rightarrow \{0,...,m-1\}$ $h:U\rightarrow \{0,...,m-1\}$ $h:U\rightarrow \{0,...,m-1\}$ { $h:U\rightarrow \{0,...,m-1\}$ , $h:U\rightarrow \{0,...,m-1\}$ . . , $h:U\rightarrow \{0,...,m-1\}$ - $h:U\rightarrow \{0,...,m-1\}$ $}(\displaystyle$ h $:$ {\ $displaystyle$ h: $U\rightarrow \{0,$ ... $m-1\}:$ $h(x)\in {0,...,m-1}$ 내의 $h(x)\in {0,...,m-1}$ 또는 슬롯을 각 h $h(x)\in {0,...,m-1}$ $h(x)\in {0,...,m-1}$ , . $h(x)\in {0,...,m-1}$ , $h(x)\in {0,...,m-1}$ - 1 { $displaystyle h(x)\in$ {0 , $m-1}$ 에 $h(x)\in {0,...,m-1}$ 배열합니다. $x\in S$ x $x\in S$ { $displaystyle$ x \ $in$ S $x\in S$ } $m<n$ m < $m<n$ \ $displaystyle$ m < $n$ } $m<n$ 。해시 함수의 기존 구현은 테이블의 모든 요소가 $U=\{0,...,u-1\}$ $U=\{0,...,u-1\}$ { $U=\{0,...,u-1\}$ , $U=\{0,...,u-1\}$ . , $U=\{0,...,u-1\}$ - $U=\{0,...,u-1\}$ $}$ { $displaystyle$ U = \ { 0 , . , u - 1 $U=\{0,...,u-1\}$ } { $displaystyle u$ }의 $u$ $비트$ 길이가 컴퓨터 ^[6]^{: 2}아키텍처의 워드 크기 내에서 제한된다는 정수 우주 가정에 기초하고 있습니다.

완벽한 $해시함수$ h $({$ $displaystyle$ h $})$ 는 $h$ S $({displaystyle$ S})의 $S$ 각 $요소$ x({ $displaystyle$ x})가 $x$ 0 ${0,...,m-1}$ ${0,...,m-1}$ - ${0,...,m-1}$ ({ $displaystyle {0, ...m-1$ ^[11]^[12]의 고유한 값에 매핑되도록 주입함수로 정의되며,^[11] 모든 키를 미리 알고 있으면 완벽한 해시함수를 생성할 수 있습니다.

정수 우주 가정

정수 우주 가정에 사용되는 해싱 방식에는 나눗셈에 의한 해싱, 곱셈에 의한 해싱, 범용 해싱, 동적 완전 해싱 및 정적 완전 ^[6]^{: 2}해싱이 포함됩니다.그러나 일반적으로 사용되는 방식은 ^[13]^{: 264}^[10]^{: 110}나눗셈별 해싱입니다.

분할별 해시

나눗셈별 해시 방식은 다음과 같습니다.^[6]^{: 2}

h(k)\=M,{\bmod {,}}n

M

서 M

(\displaystyle

M

)

은

M

x

(\displaystyle

x

\in

S

)

의

x\in S

해시 다이제스트이며 n

(\displaystyle

n

)

은

n

테이블의 크기입니다.

곱셈에 의한 해시

곱셈에 의한 해시 방식은 다음과 같습니다.^[6]^{: 2–3}

h(k)=\lfloor nMA\rfloor {,}n

A

서 A

(\displaystyle

A

)

는

A

실수값 상수입니다.곱셈에 의한 해시의 장점은 m

\

^[6]^{: 2–3}

displaystyle

m이

m

m

하지 않다는 것입니다.값

(\displaystyle

A

)

는

A

해시 함수를 생성하지만 Donald Knuth는 황금 ^[6]^{: 3}비율을 사용할 것을 권장합니다.

충돌 해결

해시를 사용하는 검색 알고리즘은 두 부분으로 구성됩니다.첫 번째 부분은 검색 키를 배열 인덱스로 변환하는 해시 함수를 계산하는 것입니다.두 개의 검색 키 해시가 동일한 배열 인덱스에 없는 것이 이상적입니다.그러나 항상 그렇지는 않으며 보이지 않는 데이터에 대해 ^[14]^{: 515}보증하는 것은 불가능합니다.따라서 알고리즘의 두 번째 부분은 충돌 해결입니다.충돌 해결을 위한 두 가지 일반적인 방법은 개별 체인과 개방형 주소 ^[5]^{: 458}지정입니다.

개별 체인

별도의 체인으로 해시 충돌 해결

버킷 배열의 헤드 레코드와의 개별 체인에 의한 해시 충돌.

별도의 체인으로 프로세스에는 각 검색 배열 인덱스에 대한 키-값 쌍이 포함된 링크 목록이 구축됩니다.충돌한 항목은 단일 링크된 목록을 통해 함께 연결되며, 이 목록을 통해 고유한 검색 ^[5]^{: 464}키로 항목에 액세스할 수 있습니다.링크 목록과의 체인을 통한 충돌 해결은 해시 테이블의 일반적인 구현 방법입니다.T $(\displaystyle$ T $)$ 와 $T$ x $(\displaystyle$ x $)$ 를 $x$ 각각 해시 테이블과 노드로 $하면$ 다음과 ^[13]^{: 258}같이 동작합니다.

체인드 해시 삽입(T, k) 링크드리스트 T [h(k)]체인드 해시 검색(T, k) 링크드리스트 T [h(k)]체인드 해시 삭제(T, k)에서 키 k를 가진 요소를 검색합니다.

요소가 숫자 또는 어휘로 비교 가능하며 전체 순서를 유지하여 목록에 삽입된 경우 실패한 ^[14]^{: 520–521}검색이 더 빨리 종료됩니다.

개별 체인을 위한 기타 데이터 구조

키를 주문하면 자기 밸런싱 바이너리 검색 트리를 사용하는 등의 "자기 조직화" 개념을 사용하는 것이 효율적일 수 있습니다.이것에 의해 이론적으로 최악의 경우는 O $O(\log {n})$ n $)\displaystyle$ O $(\log {n$ 로 낮아질 수 있습니다.단,^[14]^{: 521} 복잡성이 더해지지만,

다이내믹 퍼펙트 해싱에서는 최악의 경우 룩업의 복잡성을 $O(1)$ O $(1)$ 로 $O(1)$ 줄이기 위해 2레벨 해시 테이블이 사용됩니다.이 기술에서는 k $\style$ k 엔트리의 $k$ $k$ 은 $k^{2}$ 2 $(\$ k $^{2$ 슬롯을 $k^{2}$ 완벽한 해시 테이블로 구성되어 있으며,^[15] 최악의 경우 검색 시간과 삽입에 대한 상각 시간이 단축됩니다.연구에 따르면 어레이 기반의 개별 체인은 부하가 ^[16]^{: 99}높은 표준 링크드 리스트 방식과 비교하여 97% 더 높은 성능을 발휘하는 것으로 나타났습니다.

또한 각 버킷에 대해 퓨전 트리를 사용하는 등의 기술을 사용하면 ^[17]가능성이 높은 모든 작업에 일정한 시간이 걸립니다.

캐싱 및 참조 위치

링크 리스트의 노드가 메모리 전체에 분산되어 있는 경우, 링크 리스트의 개별 체인 실장의 링크 리스트는 공간적인 인접성(참조 장소)에 의해 캐시에 영향을 주지 않을 수 있습니다.따라서 삽입 및 검색 중에 리스트 트래버스가 발생할 수 있습니다.^[16]^{: 91}

캐시를 의식한 변형에서는 링크 리스트 또는 셀프밸런싱 바이너리 검색 트리가 다른 체인을 통해 콜리젼을 해결하기 위해 일반적으로 캐시에 적합한 다이내믹 어레이를 사용합니다.이는 어레이의 연속적인 할당 패턴이 변환 등의 하드웨어 캐시 프리페터에 의해 악용될 수 있기 때문입니다. lookaside buffer: 접근시간과 메모리 ^[18]^[19]^[20]소비를 줄입니다.

오픈 어드레싱

선형 프로브를 사용하여 열린 주소 지정을 통해 해시 충돌이 해결되었습니다(http=1)."Ted Baker"는 독특한 해시를 가지고 있지만, 그럼에도 불구하고 "John Smith"와 충돌했던 "Sandra Dee"와 충돌했다.

이 그래프는 대형 해시 테이블(캐시 크기를 훨씬 초과)에서 요소를 검색하는 데 필요한 CPU 캐시 손실의 평균 수를 체인 및 선형 검색과 비교합니다.선형 프로빙은 참조 인접성이 우수하기 때문에 성능이 향상되지만 테이블이 가득 찰수록 성능이 크게 저하됩니다.

오픈 어드레싱은 모든 엔트리 레코드가 버킷 배열 자체에 저장되고 검색을 통해 해시 해결이 실행되는 또 다른 충돌 해결 기법입니다.새 엔트리를 삽입해야 할 경우 버킷이 검사됩니다.해시된 슬롯부터 시작하여 사용 중인 슬롯이 발견될 때까지 프로브 시퀀스로 진행됩니다.항목을 검색할 때 버킷은 대상 레코드가 발견되거나 사용되지 않은 배열 슬롯이 발견될 때까지 동일한 순서로 검색됩니다. 이 슬롯은 ^[21]검색에 실패했음을 나타냅니다.

잘 알려진 프로브 시퀀스는 다음과 같습니다.

선형 프로브 - 프로브 간 간격이 고정됩니다(일반적으로 1).^[22]
2차 프로빙 - 원래 해시 ^[23]^{: 272}계산에 의해 주어진 값에 2차 다항식의 연속적인 출력을 더함으로써 프로브 사이의 간격을 증가시킵니다.
이중 해시: 프로브 간의 간격이 보조 해시 ^[23]^{: 272–273}함수에 의해 계산됩니다.

로드 계수α(\ $displaystyle \alpha})$ 가 $\alpha$ ^[8]^[16]^{: 93}1에 가까워지면 프로브 시퀀스가 증가하므로 오픈 어드레싱의 성능은 개별 체인에 비해 느릴 수 있습니다.테이블이 ^[5]^{: 471}완전히 채워진 경우 로드 계수가 1에 도달하면 프로빙에 의해 무한 루프가 발생합니다.선형 프로브의 평균 비용은 클러스터 형성이 검색 시간을 ^[5]^{: 472}증가시키기 때문에 클러스터링을 피하기 위해 테이블 전체에 요소를 균일하게 분산시키는 해시 함수의 능력에 따라 달라집니다.

캐싱 및 참조 위치

슬롯은 연속된 위치에 있으므로 선형 검색을 통해 참조의 인접성으로 인해 CPU 캐시의 활용률이 향상되어 메모리 ^[22]지연 시간이 단축될 수 있습니다.

오픈 어드레싱을 기반으로 한 기타 충돌 해결 방법

통합 해시

병합된 해시는 별도의 체인과 오픈어드레싱의 하이브리드로 버킷 또는 노드가 ^[24]^{: 6–8}테이블 내에서 링크됩니다.이 알고리즘은 고정 메모리 ^[24]^{: 4}할당에 매우 적합합니다.병합된 해시의 충돌은 해시 테이블에서 가장 큰 인덱스 빈 슬롯을 식별하여 해결되며 충돌 값이 해당 슬롯에 삽입됩니다.버킷은 충돌하는 해시 ^[24]^{: 8}주소를 포함하는 삽입된 노드의 슬롯에도 연결됩니다.

뻐꾸기 해싱

Cuckoo 해싱은 오픈 $O(1)$ 충돌 해결 기술의 한 형태로, O(1 $)\displaystyle$ O(1) 최악의 $O(1)$ 경우 룩업이 복잡해지고 삽입 시 상각 시간이 $O(1)$ 하게 유지됩니다.충돌은 각각 자체 해시 기능을 가진 2개의 해시 테이블을 유지함으로써 해결되며 충돌한 슬롯은 지정된 항목으로 대체되고 슬롯의 프리 점유된 요소는 다른 해시 테이블로 대체됩니다.이 프로세스는 모든 키가 테이블의 빈 버킷에 자체 스팟을 가질 때까지 계속됩니다.순서가 무한 루프 상태가 되면(임계값 루프 카운터를 유지함으로써 식별됨), 양쪽 해시 테이블이 새로운 해시 함수로 재플래시되고 절차가 계속됩니다.^[25]^{: 124–125}

홉스코치 해시

Hopscotch 해싱은 뻐꾸기 해싱, 선형 프로빙 및 체인의 요소를 버킷의 인근 개념으로 결합하는 오픈 어드레싱 기반 알고리즘입니다.버킷은 특정 점유된 버킷 주위에 후속 버킷으로 "가상"^[26]^{: 351–352} 버킷이라고도 합니다.이 알고리즘은 해시 테이블의 부하 계수가 90%를 초과할 때 더 나은 성능을 제공하도록 설계되었으며 동시 설정에서 높은 throughput을 제공하므로 크기가 조정 가능한 동시 해시 ^[26]^{: 350}테이블을 구현하는 데 적합합니다.사방 치기라의 근린 특성 해싱 보증을 속성, 그 동네 안에 어떤 주어진 양동이는 매우 가까운 양동이를 그 자체로는 그것을 찾는 비용에;알고리즘은 neighbourhood—with에에 포함될 가능한 비용 다른 물건들을 대체에 관련된 시도하고 원하는 항목을 찾는 비용이다.[26]:352

해시 테이블 내의 각 버킷에는 H-1 ^[26]^{: 352}엔트리 내의 현재 가상 버킷에 해시된 항목의 상대적인 거리를 나타내기 위한 H비트 배열인 추가 "홉 정보"가 포함됩니다.k{k\displaystyle}과 Bk{Bk\displaystyle} 열쇠가 되고 양동이가 키를 해시하에 각각 삽입하는, 그런 점은 알고리즘의 근린 속성을 맹세는 여러 사건이 삽입 절차에 관여한다:[26]:352–353 만약 Bk{Bk\displaystyle}는 해당 요소 inserted,자.그리고 왼쪽비트맵의 대부분의 비트는 1로 설정됩니다.빈 슬롯이 아닌 경우 테이블 내의 빈 슬롯을 찾기 위해 선형 프로브를 사용하여 버킷의 비트맵이 갱신되고 삽입이 이루어집니다.빈 슬롯이 네이버 범위 내에 있지 않은 경우(즉, H-1), 각 버킷의 후속 스왑 및 홉 정보 비트 배열 조작이 그에 따라 수행됩니다.인접 불변 속성.^[26]^{: 353}

로빈 후드 해싱

로빈 후드 해시는 개방형 어드레싱 기반 충돌 해결 알고리즘입니다. 충돌은 "홈 로케이션" 즉, 항목이 ^[27]^{: 12}해시된 버킷에서 가장 먼 요소(또는 가장 긴 프로브 시퀀스 길이(PSL))의 변위를 선호하여 해결됩니다.로빈 후드 해싱은 이론적인 검색 비용을 변경하지 않지만 ^[28]^{: 2}버킷에 있는 항목의 분산, 즉 해시 ^[29]테이블의 클러스터 형성을 처리하는 데 큰 영향을 미칩니다.로빈 후드 해시를 사용하는 해시 테이블 내의 각 노드를 추가 PSL ^[30]값을 저장하도록 확장해야 합니다. $({displaystyle$ x})를 $x$ 삽입하는 키 $,$ $x$ . $p$ $s$ l { $displaystyle$ x. $psl}$ 를 $x.psl$ (증분) PSL 길이 $({displaystyle$ x $x$ $T$ { $displaystyle$ T $}$ 를 $T$ 해시 테이블, ${displaystyle$ j $}$ 를 $j$ 인덱스로 합니다.삽입 절차는 다음과 같습니다.^[27]^{: 12–13}^[31]^{: 5}

$x.psl\ \leq \ T[j].psl$ x . $x.psl\ \leq \ T[j].psl$ s $x.psl\ \leq \ T[j].psl$ T [ $x.psl\ \leq \ T[j].psl$ . $x.psl\ \leq \ T[j].psl$ $x.psl\ \leq \ T[j].psl$ l \ $displaystyle x$ . psl \ \ $leq$ \ T [ $x.psl\ \leq \ T[j].psl$ j . psl $x.psl\ \leq \ T[j].psl$ ] : 외부 프로브를 시도하지 않고 다음 버킷으로 반복됩니다.
만약 x.ps나는>T[j]. ps나는{\displaystyle x.psl\>)T[j].psl}:){\displaystyle)}은 양동이 j{j\displaystyle}에 항목 삽입&T 와 교환하다.){\displaystyle)}[j]{T[j]\displaystyle}—let이)′{\displaystyle x'};j+1{\displaystyle j+에서 이 수사를 맡아 진행하다.1}stbucket to $insert$ x $（$ \ $displaystyle$ x ' $x'$ ） ;모든 요소가 삽입될 때까지 절차를 반복합니다.

동적 크기 조정

반복된 경우 삽입,(1)은amortized O는 조회와 삽입 작업의{O(1)\displaystyle}의 성능을 유지시킬 항목의 결국 부하율 증가가 해시 테이블 성장하기 위한 번호, 해시 테이블은 역동적으로 표 하단의 제품들은 새로운 해시 table,의 들통으로 흘러들rehashed의 크기만 조정한다.[8]모듈로 ^[32]연산으로 인해 테이블 크기가 다르므로 항목을 복사할 수 없습니다.크기 ^[33]변경은 메모리 사용을 방지하기 위해 크기에 비해 엔트리가 적은 해시 테이블에서 수행할 수 있습니다.

모든 항목을 이동하여 크기 조정

통상, 원래의 해시 테이블의 2배의 사이즈의 새로운 해시 테이블을 비공개로 할당해, 삽입 조작에 이은 항목의 해시 값을 산출해 원래의 해시 테이블내의 모든 항목을 새롭게 할당한 해시 테이블로 이동시킨다.단순함에도 불구하고 ^[34]^{: 478–479}재탕은 계산 비용이 많이 듭니다.

재이용의 대체 수단

일부 해시 테이블 구현(특히 실시간 시스템)은 시간에 중요한 작업을 중단시킬 수 있기 때문에 해시 테이블을 한 번에 확대하는 대가를 지불할 수 없습니다.동적 크기 조정을 피할 수 없는 경우 리플레이시 스토리지 블립(일반적으로 새 테이블 크기의 50%)을 방지하고 오래된 해시 ^[35]^{: 2–3}테이블로 인한 대용량 메모리 블록 할당 해제로 인해 힙 압축이 트리거되는 메모리 조각화를 방지하기 위해 서서히 크기를 조정하는 것이 해결책입니다.이 경우 해시 테이블의 버킷이 변경되지 않도록 오래된 해시 테이블에 할당된 이전 메모리 블록을 확장함으로써 리하싱 동작이 증분적으로 이루어집니다.상각된 리플레이싱의 일반적인 접근방법으로는 오래된 $h_{\text{old}}$ (\ $displaystyle h_{\$ $text{old$ $}})$ 와 $h_{\text{old}}$ $h_{\text{new}}$ 해시함수(\ $displaystyle$ h_ ${\$ text ${$ new $h_{\text{new}}$ 가 있습니다.새로운 해시 함수에 따라 버킷의 항목을 재작성하는 프로세스를 클리닝이라고 합니다. $\mathrm {Get} (\mathrm {key} )$ $\mathrm {Add} (\mathrm {key} )$ 를 명령 패턴으로 구현하려면 A d $\mathrm {Add} (\mathrm {key} )$ ( $\mathrm {Add} (\mathrm {key} )$ $\mathrm {Add} (\mathrm {key} )$ ) \ $display$ \ $mathrm$ { Add } ( \ $mathrm$ { key $}$ ) , G $\mathrm {Get} (\mathrm {key} )$ e $\mathrm {Get} (\mathrm {key} )$ ( $\mathrm {Get} (\mathrm {key} )$ $\mathrm {Get} (\mathrm {key} )$ ) \ $display style$ \ $mathrm$ { Get } ( $\ key$ ) $}$ $\mathrm {Add} (\mathrm {key} )$ 의 작업을 $\mathrm {Get} (\mathrm {key} )$ 캡슐화합니다. $\mathrm {Delete} (\mathrm {key} )$ $\mathrm {Lookup} (\mathrm {key} ,{\text{command}})$ $\mathrm {Delete} (\mathrm {key} )$ e ( $\mathrm {Delete} (\mathrm {key} )$ e y $\mathrm {Delete} (\mathrm {key} )$ ) \ $displaystyle \ mathrm$ { Delete $\mathrm {Delete} (\mathrm {key} )$ $\mathrm {Lookup} (\mathrm {key} ,{\text{command}})$ ( \ $mathrm$ { $\mathrm {Lookup} (\mathrm {key} ,{\text{command}})$ } , $\mathrm {Lookup} (\mathrm {key} ,{\text{command}})$ ) \ $displaystyle$ \ $mathrm$ { $Lookup }$ ( $\ mathrm$ { key } , { command $\mathrm {Lookup} (\mathrm {key} ,{\text{command}})$ } ) such $\mathrm {Delete} (\mathrm {key} )$ $\mathrm {Lookup} (\mathrm {key} ,{\text{command}})$ ^[35]^{: 3}such such such a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a

$\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ $\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ ( $\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ e $\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ ) $]{$ $displaystyle \mathrm$ { $Table }$ [ h $_$ { \ $text$ { $old$ } （ \ $mathrm$ { $key }$ ） } $\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ 을 $\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ $\mathrm {Table} [h_{\text{old}}(\mathrm {key} )]$ 합니다.
[ $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ y ) $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ $displaystyle \mathrm$ { $Table }$ [ $h_{\text{new}}(\mathrm {key})}$ 버킷을 $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ 합니다 $\mathrm {Table} [h_{\text{new}}(\mathrm {key} )]$ .
명령어가 실행됩니다.

선형 해시

선형 해시는 해시 테이블을 구현하여 테이블을 한 ^[36]번에1 버킷씩 동적으로 증감할 수 있도록 합니다.

성능

해시 테이블의 성능은 해시 테이블 내의 엔트리에 대한 준랜덤 번호(「\ $displaystyle$ \ $sigma$ $\sigma$ 를 생성하는 해시 함수의 능력에 따라 달라집니다. $K$ 서K(\ $displaystyle$ K $K$ $(\displaystyle$ n $)$ 및 $n$ $)$ 는 $h(x)$ 키, 버킷 수 및 해시 함수를 나타냅니다. $\sigma \ =\ h(K)\ \%\ n$ $\sigma \ =\ h(K)\ \%\ n$ ( $\sigma \ =\ h(K)\ \%\ n$ ) $\sigma \ =\ h(K)\ \%\ n$ % n \ $displaystyle$ \ $=$ \ $\sigma$ $h$ ( K ) $\$ $%$ \ n $\sigma \ =\ h(K)\ \%\ n$ 。해시 함수가 $고유$ 키( $K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})$ 1 generates $K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})$ $K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})$ ) $K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})$ $K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})$ ( $K$ ) $K_{1}\neq K_{2},\ h(K_{1})\ =\ h(K_{2})$ \ $displaystyle$ \ $k _$ { 2 \ $neQ$ _ { $2$ } 를 $생성$ 하는 $\sigma$ 경우 $.$ s. 해시 테이블 연산의 일정 시간 복잡도( $O(1)$ ( $O(1)$ ) \ $displaystyle$ O (1) $O(1)$ )는 해시 함수가 충돌 인덱스를 생성하지 않는 것을 전제로 하고 있기 때문에 해시 테이블의 성능은 선택한 해시 함수의 ^[37]^{: 1}지수 분산 능력에 정비례한다.그러나 이러한 해시함수의 구축은 실질적으로 실현 불가능하며, 따라서 구현은 더 높은 ^[37]^{: 2}성능을 달성하기 위해 사례별 충돌 해결 기술에 의존합니다.

적용들

어소시에이션 어레이

해시 테이블은 일반적으로 다양한 유형의 인메모리 테이블을 구현하기 위해 사용됩니다.관련 ^[23]배열을 구현하는 데 사용됩니다.

데이터베이스 인덱싱

해시 테이블은 디스크 기반 데이터 구조 및 데이터베이스 인덱스(dbm 등)로도 사용할 수 있지만 이러한 애플리케이션에서는 ^[38]B-tree가 더 인기가 있습니다.

캐시

해시 테이블은 주로 저속 미디어에 저장된 데이터에 대한 액세스 속도를 높이기 위해 사용되는 캐시, 보조 데이터 테이블을 구현하는 데 사용할 수 있습니다.이 응용 프로그램에서 해시 충돌은 두 개의 충돌 엔트리 중 하나를 폐기함으로써 처리할 수 있습니다.일반적으로 현재 테이블에 저장되어 있는 오래된 항목을 지우고 새 항목으로 덮어쓰므로 테이블 내의 모든 항목이 고유한 해시 ^[39]^[40]값을 가집니다.

놓다

해시 테이블은 특별한 순서 없이 고유한 값을 저장할 수 있는 set 데이터 구조의 구현에 사용할 수 있습니다. set은 일반적으로 요소 ^[41]검색 대신 컬렉션에서 값의 멤버십을 테스트하는 데 사용됩니다.

전치표

검색된 ^[42]각 섹션에 대한 정보를 저장하는 복잡한 해시 테이블로의 변환 테이블입니다.

실장

프로그래밍 언어

많은 프로그래밍 언어는 해시 테이블 기능을 내장형 연관 배열 또는 표준 라이브러리 모듈로 제공합니다.

JavaScript 에서는 7개의 "primitive" 데이터 유형을 제외한 모든 값을 "object"라고 부릅니다.이것은 정수, 문자열 또는 고유 "symbol" 원시 값을 해시 맵의 키로 사용합니다.ECMAScript 6도 추가되었습니다.Map그리고.Set데이터 ^[43]구조

C++11에는 다음이 포함됩니다.unordered_map임의의 유형의 ^[44]키와 값을 저장하기 위한 표준 라이브러리에 있습니다.

자바 프로그래밍 언어에는HashSet,HashMap,LinkedHashSet,그리고.LinkedHashMap 범용 ^[45]컬렉션

Python의 빌트인dict는 해시 테이블을 ^[46]유형 형식으로 구현합니다.

루비 빌트인Hash는, Ruby 2.^[47]4 이후의 오픈 어드레싱 모델을 사용합니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to Algorithms (3rd ed.). Massachusetts Institute of Technology. pp. 253–280. ISBN 978-0-262-03384-8.
^ 찰스 E. Leiserson, 상각 알고리즘, 표 더블링, 잠재적 방법 2009년 8월 7일 웨이백 머신 강의 13, MIT 6.046J/18.410J 알고리즘 소개 코스—2005년 가을
^ Knuth, Donald (1998). The Art of Computer Programming. Vol. 3: Sorting and Searching (2nd ed.). Addison-Wesley. pp. 513–558. ISBN 978-0-201-89685-5.
^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Chapter 11: Hash Tables". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 221–252. ISBN 978-0-262-53196-2.
^ ^a ^b ^c ^d ^e Sedgewick, Robert; Wayne, Kevin (2011). Algorithms. Vol. 1 (4 ed.). Addison-Wesley Professional – via Princeton University, Department of Computer Science.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Mehta, Dinesh P.; Sahni, Sartaj (October 28, 2004). "9: Hash Tables". Handbook of Datastructures and Applications (1 ed.). Taylor & Francis. doi:10.1201/9781420035179. ISBN 978-1-58488-435-4.
^ ^a ^b ^c Konheim, Alan G. (June 21, 2010). Hashing in Computer Science: Fifty Years of Slicing and Dicing. John Wiley & Sons, Inc. doi:10.1002/9780470630617. ISBN 9780470630617.
^ ^a ^b ^c ^d Mayers, Andrew (2008). "CS 312: Hash tables and amortized analysis". Cornell University, Department of Computer Science. Archived from the original on April 26, 2021. Retrieved October 26, 2021 – via cs.cornell.edu.
^ Maurer, W.D.; Lewis, T.G. (March 1, 1975). "Hash Table Methods". ACM Computing Surveys. Journal of the ACM. 1 (1): 14. doi:10.1145/356643.356645. S2CID 17874775.
^ ^a ^b Owolabi, Olumide (February 1, 2003). "Empirical studies of some hashing functions". Information and Software Technology. Department of Mathematics and Computer Science, University of Port Harcourt. 45 (2): 109–112. doi:10.1016/S0950-5849(02)00174-X – via ScienceDirect.
^ ^a ^b Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006), "Perfect Hashing for Network Applications", 2006 IEEE International Symposium on Information Theory: 2774–2778, doi:10.1109/ISIT.2006.261567, ISBN 1-4244-0505-X, S2CID 1494710
^ Belazzougui, Djamal; Botelho, Fabiano C.; Dietzfelbinger, Martin (2009), "Hash, displace, and compress" (PDF), Algorithms—ESA 2009: 17th Annual European Symposium, Copenhagen, Denmark, September 7-9, 2009, Proceedings (PDF), Lecture Notes in Computer Science, vol. 5757, Berlin: Springer, pp. 682–693, CiteSeerX 10.1.1.568.130, doi:10.1007/978-3-642-04128-0_61, MR 2557794
^ ^a ^b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Chapter 11: Hash Tables". Introduction to Algorithms (2nd ed.). Massachusetts Institute of Technology. ISBN 978-0-262-53196-2.
^ ^a ^b ^c Donald E. Knuth (April 24, 1998). The Art of Computer Programming: Volume 3: Sorting and Searching. Addison-Wesley Professional. ISBN 978-0-201-89685-5.
^ Erik Demain, Jeff Lind. 6.897: Advanced Data Structures.MIT 컴퓨터 과학 및 인공지능 연구소.2003년 봄 : CS1 유지보수 : 타이틀로서의 아카이브 복사 (링크)
^ ^a ^b ^c Askitis, Nikolas; Zobel, Justin (2005). "Cache-Conscious Collision Resolution in String Hash Tables". International Symposium on String Processing and Information Retrieval. Springer Science+Business Media: 91–102. doi:10.1007/11575832_1. ISBN 978-3-540-29740-6.
^ 를 클릭합니다Willard, Dan E. (2000). "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree". SIAM Journal on Computing. 29 (3): 1030–1049. doi:10.1137/S0097539797322425. MR 1740562..
^ Askitis, Nikolas; Sinha, Ranjan (2010). "Engineering scalable, cache and space efficient tries for strings". The VLDB Journal. 17 (5): 634. doi:10.1007/s00778-010-0183-9. ISSN 1066-8888. S2CID 432572.
^ Askitis, Nikolas; Zobel, Justin (October 2005). Cache-conscious Collision Resolution in String Hash Tables. Proceedings of the 12th International Conference, String Processing and Information Retrieval (SPIRE 2005). Vol. 3772/2005. pp. 91–102. doi:10.1007/11575832_11. ISBN 978-3-540-29740-6.
^ Askitis, Nikolas (2009). Fast and Compact Hash Tables for Integer Keys (PDF). Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009). Vol. 91. pp. 113–122. ISBN 978-1-920682-72-9. Archived from the original (PDF) on February 16, 2011. Retrieved June 13, 2010.
^ Tenenbaum, Aaron M.; Langsam, Yedidyah; Augenstein, Moshe J. (1990). Data Structures Using C. Prentice Hall. pp. 456–461, p. 472. ISBN 978-0-13-199746-2.
^ ^a ^b Pagh, Rasmus; Rodler, Flemming Friche (2001). "Cuckoo Hashing". Algorithms — ESA 2001. Lecture Notes in Computer Science. Vol. 2161. pp. 121–133. CiteSeerX 10.1.1.25.4189. doi:10.1007/3-540-44676-1_10. ISBN 978-3-540-42493-2.
^ ^a ^b ^c 를 클릭합니다Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), "11 Hash Tables", Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, pp. 221–252, ISBN 0-262-03293-7.
^ ^a ^b ^c Vitter, Jeffery S.; Chen, Wen-Chin (1987). The design and analysis of coalesced hashing. New York, United States: Oxford University Press. ISBN 978-0-19-504182-8 – via Archive.org.
^ Pagh, Rasmus; Rodler, Flemming Friche (2001). "Cuckoo Hashing". Algorithms — ESA 2001. Lecture Notes in Computer Science. Vol. 2161. CiteSeerX 10.1.1.25.4189. doi:10.1007/3-540-44676-1_10. ISBN 978-3-540-42493-2.
^ ^a ^b ^c ^d ^e ^f Herlihy, Maurice; Shavit, Nir; Tzafrir, Moran (2008). "Hopscotch Hashing". International Symposium on Distributed Computing. Distributed Computing. Berlin, Heidelberg: Springer Publishing. 5218: 350–364. doi:10.1007/978-3-540-87779-0_24. ISBN 978-3-540-87778-3 – via Springer Link.
^ ^a ^b Celis, Pedro (1986). Robin Hood Hashing (PDF). Ontario, Canada: University of Waterloo, Dept. of Computer Science. ISBN 031529700X. OCLC 14083698. Archived (PDF) from the original on November 1, 2021. Retrieved November 2, 2021.
^ Poblete, P.V.; Viola, A. (August 14, 2018). "Analysis of Robin Hood and Other Hashing Algorithms Under the Random Probing Model, With and Without Deletions". Combinatorics, Probability and Computing. Cambridge University Press. 28 (4): 600–617. doi:10.1017/S0963548318000408. ISSN 1469-2163. S2CID 125374363. Retrieved November 1, 2021 – via Cambridge Core.
^ Clarkson, Michael (2014). "Lecture 13: Hash tables". Cornell University, Department of Computer Science. Archived from the original on October 7, 2021. Retrieved November 1, 2021 – via cs.cornell.edu.
^ Gries, David (2017). "JavaHyperText and Data Structure: Robin Hood Hashing" (PDF). Cornell University, Department of Computer Science. Archived (PDF) from the original on April 26, 2021. Retrieved November 2, 2021 – via cs.cornell.edu.
^ Celis, Pedro (March 28, 1988). External Robin Hood Hashing (PDF) (Technical report). Bloomington, Indiana: Indiana University, Department of Computer Science. 246. Archived (PDF) from the original on November 2, 2021. Retrieved November 2, 2021.
^ Goddard, Wayne (2021). "Chater C5: Hash Tables" (PDF). Clemson University. pp. 15–16. Archived (PDF) from the original on November 9, 2021. Retrieved November 9, 2021 – via people.cs.clemson.edu.
^ Devadas, Srini; Demaine, Erik (February 25, 2011). "Intro to Algorithms: Resizing Hash Tables" (PDF). Massachusetts Institute of Technology, Department of Computer Science. Archived (PDF) from the original on May 7, 2021. Retrieved November 9, 2021 – via MIT OpenCourseWare.
^ Thareja, Reema (October 13, 2018). "Hashing and Collision". Data Structures Using C (2 ed.). Oxford University Press. ISBN 9780198099307.
^ ^a ^b Friedman, Scott; Krishnan, Anand; Leidefrost, Nicholas (March 18, 2003). "Hash Tables for Embedded and Real-time systems" (PDF). All Computer Science and Engineering Research. Washington University in St. Louis. doi:10.7936/K7WD3XXV. Archived (PDF) from the original on June 9, 2021. Retrieved November 9, 2021 – via Northwestern University, Department of Computer Science.
^ Litwin, Witold (1980). "Linear hashing: A new tool for file and table addressing" (PDF). Proc. 6th Conference on Very Large Databases. Carnegie Mellon University. pp. 212–223. Archived (PDF) from the original on May 6, 2021. Retrieved November 10, 2021 – via cs.cmu.edu.
^ ^a ^b Dijk, Tom Van (2010). "Analysing and Improving Hash Table Performance" (PDF). Netherlands: University of Twente. Archived (PDF) from the original on November 6, 2021. Retrieved December 31, 2021.
^ Lech Banachowski. "Indexes and external sorting". pl:Polsko-Japońska Akademia Technik Komputerowych. Archived from the original on March 26, 2022. Retrieved March 26, 2022.
^ Zhong, Liang; Zheng, Xueqian; Liu, Yong; Wang, Mengting; Cao, Yang (February 2020). "Cache hit ratio maximization in device-to-device communications overlaying cellular networks". China Communications. 17 (2): 232–238. doi:10.23919/jcc.2020.02.018. ISSN 1673-5447. S2CID 212649328.
^ Bottommley, James (January 1, 2004). "Understanding Caching". Linux Journal. Archived from the original on December 4, 2020. Retrieved April 16, 2022.
^ Jill Seaman (2014). "Set & Hash Tables". Texas State University. Archived from the original (PDF) on March 26, 2022. Retrieved March 26, 2022.
^ "Transposition Table - Chessprogramming wiki". chessprogramming.org. Archived from the original on February 14, 2021. Retrieved May 1, 2020.
^ "JavaScript data types and data structures - JavaScript MDN". developer.mozilla.org. Retrieved July 24, 2022.
^ "Programming language C++ - Technical Specification" (PDF). International Organization for Standardization. pp. 812–813. Archived from the original (PDF) on January 21, 2022. Retrieved February 8, 2022.
^ "Lesson: Implementations (The Java™ Tutorials > Collections)". docs.oracle.com. Archived from the original on January 18, 2017. Retrieved April 27, 2018.
^ Zhang, Juan; Jia, Yunwei (2020). "Redis rehash optimization based on machine learning". Journal of Physics: Conference Series. 1453 (1): 3. Bibcode:2020JPhCS1453a2048Z. doi:10.1088/1742-6596/1453/1/012048. S2CID 215943738.
^ Jonan Scheffler (December 25, 2016). "Ruby 2.4 Released: Faster Hashes, Unified Integers and Better Rounding". heroku.com. Archived from the original on July 3, 2019. Retrieved July 3, 2019.

추가 정보

Tamassia, Roberto; Goodrich, Michael T. (2006). "Chapter Nine: Maps and Dictionaries". Data structures and algorithms in Java : [updated for Java 5.0] (4th ed.). Hoboken, NJ: Wiley. pp. 369–418. ISBN 978-0-471-73884-8.
McKenzie, B. J.; Harries, R.; Bell, T. (February 1990). "Selecting a hashing algorithm". Software: Practice and Experience. 20 (2): 209–224. doi:10.1002/spe.4380200207. hdl:10092/9691. S2CID 12854386.

외부 링크

해시 테이블의 NIST 엔트리
개방형 데이터 구조 – 5장 – 해시 테이블, Pat Morin
MIT 알고리즘 소개: 해싱 1 MIT OCW 강의 비디오
MIT 알고리즘 소개: 해싱 2 MIT OCW 강의 비디오

[Cormen_et_al-1] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to Algorithms (3rd ed.). Massachusetts Institute of Technology. pp. 253–280. ISBN 978-0-262-03384-8.

[leiser-2] 찰스 E. Leiserson, 상각 알고리즘, 표 더블링, 잠재적 방법 2009년 8월 7일 웨이백 머신 강의 13, MIT 6.046J/18.410J 알고리즘 소개 코스—2005년 가을

[knuth-3] Knuth, Donald (1998). The Art of Computer Programming. Vol. 3: Sorting and Searching (2nd ed.). Addison-Wesley. pp. 513–558. ISBN 978-0-201-89685-5.

[cormen-4] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Chapter 11: Hash Tables". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 221–252. ISBN 978-0-262-53196-2.

[algo1rob-5] Sedgewick, Robert; Wayne, Kevin (2011). Algorithms. Vol. 1 (4 ed.). Addison-Wesley Professional – via Princeton University, Department of Computer Science.

[hashhist-6] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m Mehta, Dinesh P.; Sahni, Sartaj (October 28, 2004). "9: Hash Tables". Handbook of Datastructures and Applications (1 ed.). Taylor & Francis. doi:10.1201/9781420035179. ISBN 978-1-58488-435-4.

[Konheim-7] Konheim, Alan G. (June 21, 2010). Hashing in Computer Science: Fifty Years of Slicing and Dicing. John Wiley & Sons, Inc. doi:10.1002/9780470630617. ISBN 9780470630617.

[cornell08-8] Mayers, Andrew (2008). "CS 312: Hash tables and amortized analysis". Cornell University, Department of Computer Science. Archived from the original on April 26, 2021. Retrieved October 26, 2021 – via cs.cornell.edu.

[9] Maurer, W.D.; Lewis, T.G. (March 1, 1975). "Hash Table Methods". ACM Computing Surveys. Journal of the ACM. 1 (1): 14. doi:10.1145/356643.356645. S2CID 17874775.

[owo03-10] Owolabi, Olumide (February 1, 2003). "Empirical studies of some hashing functions". Information and Software Technology. Department of Mathematics and Computer Science, University of Port Harcourt. 45 (2): 109–112. doi:10.1016/S0950-5849(02)00174-X – via ScienceDirect.

[Yi06-11] Lu, Yi; Prabhakar, Balaji; Bonomi, Flavio (2006), "Perfect Hashing for Network Applications", 2006 IEEE International Symposium on Information Theory: 2774–2778, doi:10.1109/ISIT.2006.261567, ISBN 1-4244-0505-X, S2CID 1494710

[CHD-12] Belazzougui, Djamal; Botelho, Fabiano C.; Dietzfelbinger, Martin (2009), "Hash, displace, and compress" (PDF), Algorithms—ESA 2009: 17th Annual European Symposium, Copenhagen, Denmark, September 7-9, 2009, Proceedings (PDF), Lecture Notes in Computer Science, vol. 5757, Berlin: Springer, pp. 682–693, CiteSeerX 10.1.1.568.130, doi:10.1007/978-3-642-04128-0_61, MR 2557794

[cormenalgo01-13] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Chapter 11: Hash Tables". Introduction to Algorithms (2nd ed.). Massachusetts Institute of Technology. ISBN 978-0-262-53196-2.

[donald3-14] Donald E. Knuth (April 24, 1998). The Art of Computer Programming: Volume 3: Sorting and Searching. Addison-Wesley Professional. ISBN 978-0-201-89685-5.

[15] Erik Demain, Jeff Lind. 6.897: Advanced Data Structures.MIT 컴퓨터 과학 및 인공지능 연구소.2003년 봄 : CS1 유지보수 : 타이틀로서의 아카이브 복사 (링크)

[nick05-16] Askitis, Nikolas; Zobel, Justin (2005). "Cache-Conscious Collision Resolution in String Hash Tables". International Symposium on String Processing and Information Retrieval. Springer Science+Business Media: 91–102. doi:10.1007/11575832_1. ISBN 978-3-540-29740-6.

[17] 를 클릭합니다Willard, Dan E. (2000). "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree". SIAM Journal on Computing. 29 (3): 1030–1049. doi:10.1137/S0097539797322425. MR 1740562..

[18] Askitis, Nikolas; Sinha, Ranjan (2010). "Engineering scalable, cache and space efficient tries for strings". The VLDB Journal. 17 (5): 634. doi:10.1007/s00778-010-0183-9. ISSN 1066-8888. S2CID 432572.

[19] Askitis, Nikolas; Zobel, Justin (October 2005). Cache-conscious Collision Resolution in String Hash Tables. Proceedings of the 12th International Conference, String Processing and Information Retrieval (SPIRE 2005). Vol. 3772/2005. pp. 91–102. doi:10.1007/11575832_11. ISBN 978-3-540-29740-6.

[20] Askitis, Nikolas (2009). Fast and Compact Hash Tables for Integer Keys (PDF). Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009). Vol. 91. pp. 113–122. ISBN 978-1-920682-72-9. Archived from the original (PDF) on February 16, 2011. Retrieved June 13, 2010.

[tenenbaum90-21] Tenenbaum, Aaron M.; Langsam, Yedidyah; Augenstein, Moshe J. (1990). Data Structures Using C. Prentice Hall. pp. 456–461, p. 472. ISBN 978-0-13-199746-2.

[Cuckoo-22] Pagh, Rasmus; Rodler, Flemming Friche (2001). "Cuckoo Hashing". Algorithms — ESA 2001. Lecture Notes in Computer Science. Vol. 2161. pp. 121–133. CiteSeerX 10.1.1.25.4189. doi:10.1007/3-540-44676-1_10. ISBN 978-3-540-42493-2.

[clrs-23] 를 클릭합니다Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001), "11 Hash Tables", Introduction to Algorithms (2nd ed.), MIT Press and McGraw-Hill, pp. 221–252, ISBN 0-262-03293-7.

[chen87-24] Vitter, Jeffery S.; Chen, Wen-Chin (1987). The design and analysis of coalesced hashing. New York, United States: Oxford University Press. ISBN 978-0-19-504182-8 – via Archive.org.

[25] Pagh, Rasmus; Rodler, Flemming Friche (2001). "Cuckoo Hashing". Algorithms — ESA 2001. Lecture Notes in Computer Science. Vol. 2161. CiteSeerX 10.1.1.25.4189. doi:10.1007/3-540-44676-1_10. ISBN 978-3-540-42493-2.

[nir08-26] ^ ^a ^b ^c ^d ^e ^f Herlihy, Maurice; Shavit, Nir; Tzafrir, Moran (2008). "Hopscotch Hashing". International Symposium on Distributed Computing. Distributed Computing. Berlin, Heidelberg: Springer Publishing. 5218: 350–364. doi:10.1007/978-3-540-87779-0_24. ISBN 978-3-540-87778-3 – via Springer Link.

[waterloo86-27] Celis, Pedro (1986). Robin Hood Hashing (PDF). Ontario, Canada: University of Waterloo, Dept. of Computer Science. ISBN 031529700X. OCLC 14083698. Archived (PDF) from the original on November 1, 2021. Retrieved November 2, 2021.

[28] Poblete, P.V.; Viola, A. (August 14, 2018). "Analysis of Robin Hood and Other Hashing Algorithms Under the Random Probing Model, With and Without Deletions". Combinatorics, Probability and Computing. Cambridge University Press. 28 (4): 600–617. doi:10.1017/S0963548318000408. ISSN 1469-2163. S2CID 125374363. Retrieved November 1, 2021 – via Cambridge Core.

[cornell14-29] Clarkson, Michael (2014). "Lecture 13: Hash tables". Cornell University, Department of Computer Science. Archived from the original on October 7, 2021. Retrieved November 1, 2021 – via cs.cornell.edu.

[30] Gries, David (2017). "JavaHyperText and Data Structure: Robin Hood Hashing" (PDF). Cornell University, Department of Computer Science. Archived (PDF) from the original on April 26, 2021. Retrieved November 2, 2021 – via cs.cornell.edu.

[indiana88-31] Celis, Pedro (March 28, 1988). External Robin Hood Hashing (PDF) (Technical report). Bloomington, Indiana: Indiana University, Department of Computer Science. 246. Archived (PDF) from the original on November 2, 2021. Retrieved November 2, 2021.

[32] Goddard, Wayne (2021). "Chater C5: Hash Tables" (PDF). Clemson University. pp. 15–16. Archived (PDF) from the original on November 9, 2021. Retrieved November 9, 2021 – via people.cs.clemson.edu.

[33] Devadas, Srini; Demaine, Erik (February 25, 2011). "Intro to Algorithms: Resizing Hash Tables" (PDF). Massachusetts Institute of Technology, Department of Computer Science. Archived (PDF) from the original on May 7, 2021. Retrieved November 9, 2021 – via MIT OpenCourseWare.

[34] Thareja, Reema (October 13, 2018). "Hashing and Collision". Data Structures Using C (2 ed.). Oxford University Press. ISBN 9780198099307.

[scott03-35] Friedman, Scott; Krishnan, Anand; Leidefrost, Nicholas (March 18, 2003). "Hash Tables for Embedded and Real-time systems" (PDF). All Computer Science and Engineering Research. Washington University in St. Louis. doi:10.7936/K7WD3XXV. Archived (PDF) from the original on June 9, 2021. Retrieved November 9, 2021 – via Northwestern University, Department of Computer Science.

[36] Litwin, Witold (1980). "Linear hashing: A new tool for file and table addressing" (PDF). Proc. 6th Conference on Very Large Databases. Carnegie Mellon University. pp. 212–223. Archived (PDF) from the original on May 6, 2021. Retrieved November 10, 2021 – via cs.cmu.edu.

[dijk10-37] Dijk, Tom Van (2010). "Analysing and Improving Hash Table Performance" (PDF). Netherlands: University of Twente. Archived (PDF) from the original on November 6, 2021. Retrieved December 31, 2021.

[38] Lech Banachowski. "Indexes and external sorting". pl:Polsko-Japońska Akademia Technik Komputerowych. Archived from the original on March 26, 2022. Retrieved March 26, 2022.

[39] Zhong, Liang; Zheng, Xueqian; Liu, Yong; Wang, Mengting; Cao, Yang (February 2020). "Cache hit ratio maximization in device-to-device communications overlaying cellular networks". China Communications. 17 (2): 232–238. doi:10.23919/jcc.2020.02.018. ISSN 1673-5447. S2CID 212649328.

[40] Bottommley, James (January 1, 2004). "Understanding Caching". Linux Journal. Archived from the original on December 4, 2020. Retrieved April 16, 2022.

[41] Jill Seaman (2014). "Set & Hash Tables". Texas State University. Archived from the original (PDF) on March 26, 2022. Retrieved March 26, 2022.

[42] "Transposition Table - Chessprogramming wiki". chessprogramming.org. Archived from the original on February 14, 2021. Retrieved May 1, 2020.

[43] "JavaScript data types and data structures - JavaScript MDN". developer.mozilla.org. Retrieved July 24, 2022.

[44] "Programming language C++ - Technical Specification" (PDF). International Organization for Standardization. pp. 812–813. Archived from the original (PDF) on January 21, 2022. Retrieved February 8, 2022.

[45] "Lesson: Implementations (The Java™ Tutorials > Collections)". docs.oracle.com. Archived from the original on January 18, 2017. Retrieved April 27, 2018.

[46] Zhang, Juan; Jia, Yunwei (2020). "Redis rehash optimization based on machine learning". Journal of Physics: Conference Series. 1453 (1): 3. Bibcode:2020JPhCS1453a2048Z. doi:10.1088/1742-6596/1453/1/012048. S2CID 215943738.

[47] Jonan Scheffler (December 25, 2016). "Ruby 2.4 Released: Faster Hashes, Unified Integers and Better Rounding". heroku.com. Archived from the original on July 3, 2019. Retrieved July 3, 2019.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

v t 잘 알려진 데이터 구조
종류들	수집 컨테이너.
추상적인	연관 배열 멀티맵 데이터 구조 검색 목록. 스택 큐 더블 엔드 큐 priority 큐 이중 엔드 priority 큐 세트 멀티셋 디조인트 세트
어레이	비트 배열 순환 버퍼 다이내믹 어레이 해시 테이블 해시 어레이 트리 희박 행렬
링크되어 있다	어소시에이션리스트 링크 리스트 스킵 리스트 언롤링된 링크 리스트 XOR 링크 리스트
나무들	B-트리 이진 검색 트리 AA나무 AVL 트리 붉은색-검은색 셀프밸런싱 트리 스플레이 트리 히프 이진 힙 이항 힙 피보나치 힙 R 트리 R* 트리 R+ 트리 힐베르트 R-트리 트리 해시 트리
그래프	이항 결정도 방향 비순환 그래프 지시 비순환 단어 그래프
데이터 구조 목록

Search

해시 테이블

네임스페이스

더

목차

역사

개요

부하율

해시함수

정수 우주 가정

분할별 해시

곱셈에 의한 해시

충돌 해결

개별 체인

개별 체인을 위한 기타 데이터 구조

캐싱 및 참조 위치

오픈 어드레싱

캐싱 및 참조 위치

오픈 어드레싱을 기반으로 한 기타 충돌 해결 방법

통합 해시

뻐꾸기 해싱

홉스코치 해시

로빈 후드 해싱

동적 크기 조정

모든 항목을 이동하여 크기 조정

재이용의 대체 수단

선형 해시

성능

적용들

어소시에이션 어레이

데이터베이스 인덱싱

캐시

놓다

전치표

실장

프로그래밍 언어

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

해시 테이블

역사

개요

부하율

해시함수

정수 우주 가정

분할별 해시

곱셈에 의한 해시

충돌 해결

개별 체인

개별 체인을 위한 기타 데이터 구조

캐싱 및 참조 위치

오픈 어드레싱

캐싱 및 참조 위치

오픈 어드레싱을 기반으로 한 기타 충돌 해결 방법

통합 해시

뻐꾸기 해싱

홉스코치 해시

로빈 후드 해싱

동적 크기 조정

모든 항목을 이동하여 크기 조정

재이용의 대체 수단

선형 해시

성능

적용들

어소시에이션 어레이

데이터베이스 인덱싱

캐시

놓다

전치표

실장

프로그래밍 언어

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.