여러 개의 복잡한 변수의 특수 함수
야코비의 세타 함수 θ1 ( n + 1 ) n ( 2 n + 1 ) z = 2 q 14 ∑ n = 0 ∞ ( - 1 ) n q n ( n + 1 ) sin = - ∞ n = - ∞ n ( - 1 ) n q ( - 1 ) n q ( n + 1 ) n ( n + 1 ) 2 ( n + 2 ( n + 2 ) 2 ( n + 2 q _ q _ begin 1 ) { } { } { π π 1 τ ∑ θ {\ } jacob style ) ( 2 \&=\sum _{n=-\infty}^{\infty}(-1)^{n-{\frac{1}{2}}q^{\left(n+{\frac{1}{2}}\right)^{2}}e^{(2n+1)iz}. \end{aligned}}} 수학 에서 세타 함수 는 여러 개의 복잡한 변수의 특수 함수입니다.그들은 아벨어의 다양성, 모듈리 공간, 2차 형태, 솔리톤 을 포함 한 많은 주제에서 나타납니다. 그들은 그라스 만 대수학으로 양자장 [1] 이론 에 등장합니다.
세타 함수의 가장 일반적인 형태는 타원 함수 이론에서 발생하는 것입니다. 복소 변수 중 하나(통칭 z)와 관련하여, 세타 함수는 관련 타원 함수의 기간 추가와 관련하여 동작을 표현하는 특성을 가지고 있어 준주기 함수가 됩니다. 추상 이론에서 이 준주기성은 하강 조건 인 복소 토러스의 선다발 의 코호몰로지 클래스에서 비롯됩니다.
열 방정식을 다룰 때 세타 함수에 대한 한 가지 해석은 "세타 함수는 특정 경계 [2]
이 eπiτ α{\ pi i\tau}^{\alpha } [note 1] 지점 선택 문제를 해결하기 위해) eα πiτi ▁{\{\alpha \piii\tau
야코비 세타 함수 Jacobi theta 함수라고 불리는 밀접하게 관련된 함수들 이 몇 개 있고, 그것들을 위한 많은 상이하고 양립 할 수 없는 표기 체계 가 있습니다. 하나 의 야코비 세타 함수(칼 구스타프 야코비의 이름 을 따서 명명됨)는 두 개의 복소수 z 와 π 에 대해 정의된 함수입니다. 여기 서 z는 임의의 복소수이고 π 는 반주기 비율이며, 이는 양의 가상 부분을 가지고 있다는 것을 의미합니다.그것은 공식에 의해 주어집니다.
ϑ ( z ; τ ) = ∑ n = − ∞ ∞ 해외의 ( π i n 2 τ + 2 π i n z ) = 1 + 2 ∑ n = 1 ∞ q n 2 코스 ( 2 π n z ) = ∑ n = − ∞ ∞ q n 2 η n 표시(\style{aligned}\vartheta(z;\filename)&=\sum _{n=-\infty}^{\infty}\exp \left(\piin^{2}\sum +2\piinz\right)\"q{n=1}^{\infty}\cos(2\piinfty)\cos(2)\cos(2\cos)\cos(2\" \&=\sum _{n=-\infty}^{\infty}q^{n^{2}}\eta^{n}\end{aligned}}} 여기 q = exp(πiτ ) 는 nom 이고 η ) 입니다.그것은 자코비 형태입니다. 이 제한은 절대 수렴 열임을 보장합니다. 고정 π 에서, 이것은 z 의 1주기 전체 함수에 대한 푸리에 급수입니다. 따라서 세타 함수는 z: 1주기 함수입니다.
ϑ ( z + 1 ; τ ) = ϑ ( z ; τ ) . displaystyle \vartheta (z+1;\vartheta )=\vartheta (z;\vartheta)} 제곱을 완성함 으로써, z 단위 로 π-준주기적이며, 다음과 같이 정의됩니다.
ϑ ( z + τ ; τ ) = 해외의 ( − π i ( τ + 2 z ) ) ϑ ( z ; τ ) . {\displaystyle \vartheta (z+\timeout;\timeout)=\exp \bigl (}-\pii(\timeout +2z){\bigr )}\vartheta (z;\timeout)} 그러므로, 일반적으로,
ϑ ( z + a + b τ ; τ ) = 해외의 ( − π i b 2 τ − 2 π i b z ) ϑ ( z ; τ ) {\displaystyle \vartheta (z+a+b\delays;\delays)=\exp \lefts\piib^{2}\delay -2\piibz\right)\vartheta (z;\delays)} 임의의 정수 a 와 b에 대하여.
임의의 고정된 π\displaystyle \tau에 대하여, 함수는 복소평면의 전체 함수이므로, 리우빌의 정리에 따르면, 상수가 아니면 1, π\displaystyle 1,\tau에서 이중 주기를 가질 수 없으며, 따라서 우리가 할 수 있는 최선은 1에서 주기를, π\displaystyle \tau에서 준주기를 만드는 것이다
ϑ ( z + a + b τ ; τ ) ϑ ( z ; τ ) = 해외의 ( π ( b 2 ℑ ( τ ) + 2 b ℑ ( z ) ) ) 표시 스타일 \left{frac{\vartheta(z+a+b\beta)}{\vartheta(z;\beta)}\right =\exp \left(\pi(b^{2}\Im(\beta))+2b\Im(z)\right} 그리고 Δ Δ 0 displaystyle \Im (\tau) 0 z , Δ ) vartheta (z,\tau)
이 함수는 다음과 같은 [3]
정리 - 만약 f : C → C \displaystyle f:\mathbb {C} \to \mathbb {C}가 완전하고 일정하지 않고 함수 방정식 {f(z + 1) = f(z + 1) = ea + 2 π if (z + 1) \\displaystyle b(z + 1) \f (z + 2) \f (z ) \displaystyle b(b)에 대해 상수를 표시합니다.
a = 0 {\displaystyle a = 0 }이면 b = \displaystyle b = \displaystyle f(z)=e^{2\piiz}이면 f (z) = -2 i {\piiz}이면 f (z) = C = (z + 1 τ + 2 tau + ∈ b tau ) {f (z + 0 } C }: 0 (cart {f + 0 }) \z + 0 ( ).
q 다른 iπτ θ 1 오른쪽 사진의 검은 점은 q 가 τ에 따라 어떻게 변하는지를 나타냅니다. q 다른 iπτ θ 1 오른쪽 사진의 검은 점은 q 가 τ에 따라 어떻게 변하는지를 나타냅니다. 보조 기능 위에서 정의한 야코비 세타 함수는 때때로 세 가지 보조 세타 함수와 함께 고려되며, 이 경우 이중 0 첨자로 작성됩니다.
ϑ 00 ( z ; τ ) = ϑ ( z ; τ ) {\displaystyle \vartheta _{00}(z;\deta)=\vartheta(z;\deta)} 표시 보조(또는 반주기) 함수는 다음과 같이 정의됩니다.
ϑ 01 ( z ; τ ) = ϑ ( z + 1 2 ; τ ) ϑ 10 ( z ; τ ) = 해외의 ( 1 4 π i τ + π i z ) ϑ ( z + 1 2 τ ; τ ) ϑ 11 ( z ; τ ) = 해외의 ( 1 4 π i τ + π i ( z + 1 2 ) ) ϑ ( z + 1 2 τ + 1 2 ; τ ) . 표시(\style{aligned}\vartheta_{01}(z;\tfrac{1}{2}};\tfrac \right)\[3pt]\vartheta_{10}(z;\tfrac)&=\exp \tp \tfrac{1}\pi\pi\piziz\right)\vart{ta\ta\ta\ta}\right}\ta\ta\ta\ta\ta\right}\right}\ta\ta {1}{2}}\right)\right)\ 바르테타 \left(z+{\tfrac {1}{2}}\tfrac +{\tfrac {1}{2}};\tfrac \right). \end{aligned}}} 이 표기법은 리만과 뭄포드 를 따르며 , 야코비의 원래 공식은 γ 가 아닌 nom q iπτ 야코비의 표기법에서 γ-함수는 다음과 같습니다.
θ 1 ( z ; q ) = θ 1 ( π z , q ) = − ϑ 11 ( z ; τ ) θ 2 ( z ; q ) = θ 2 ( π z , q ) = ϑ 10 ( z ; τ ) θ 3 ( z ; q ) = θ 3 ( π z , q ) = ϑ 00 ( z ; τ ) θ 4 ( z ; q ) = θ 4 ( π z , q ) = ϑ 01 ( z ; τ ) 표시(\style{aligned}\theta _{1}(z;q)&=\theta _{11}(z;\ta)=-\vartheta _{2}(z;q)&=\theta _{2}(\piz,q)=\ta _{3}(z;q)\ta _{ta}(\ta)\ta_{ta(\ta}\ta(\ta_ta_{ta)\ta(\ta_ta_ta_ta_ta 야코비테타 1 야코비테타 2 야코비테타 3 야코비 테타 4 위의 자코비 세타 함수의 정의는 결코 고유하지 않습니다. 자세한 내용은 Jacobi theta 함수(표기형 변동) 를 참조하십시오.
위의 세타 함수에서 z = 0 을 설정 π 만의 네 가지 함수를 얻습니다. 세타 함수 식에서 왼쪽 항목이 무효화되기 때문에 이러한 함수를 제로 값에 대한 독일어 용어에 기초하여 세타 Nullwert 함수라고 합니다 . 또는 단위 디스크 1 displaystyle q } q 만의 네 가지 함수를 얻습니다. 이들 을 [note 2] 세타 상수라고 부르기도 합니다.
ϑ 11 ( 0 ; τ ) = − θ 1 ( q ) = − ∑ n = − ∞ ∞ ( − 1 ) n − 1 / 2 q ( n + 1 / 2 ) 2 ϑ 10 ( 0 ; τ ) = θ 2 ( q ) = ∑ n = − ∞ ∞ q ( n + 1 / 2 ) 2 ϑ 00 ( 0 ; τ ) = θ 3 ( q ) = ∑ n = − ∞ ∞ q n 2 ϑ 01 ( 0 ; τ ) = θ 4 ( q ) = ∑ n = − ∞ ∞ ( − 1 ) n q n 2 표시({style{aligned})\vartheta _{11}(0;\time)&=-\theta _{1}(q)=-\sum _{n=-\infty}^{\infty}(-1)^{n-1/2}q{(n+1/2) ^{2}}\\\\vartheta _{10}(0;\deta)&=\theta _{2}(q)=\sum _{n=-\infty}^{\infty}q^{(n+1/2) ^{2}}\\\vartheta _{00}(0;\deta)&\theta _{3}(q)=\sum _{n=-\infty}^{n^{2}}^{\infty}^{{01}(0;\deta)&=\theta _{4}{n=\infty}(q){n}{n^{n^{n^{n}}}}{n^{n^{n^{n^{}}}}}}}}}}}}}{{{ q = e iπτ θ q {{displaystyle \theta {1}(q 0} 모듈러 형태를 정의하고 특정 곡선을 매개변수화하는 데 사용될 수 있습니다. 특히, 자코비 항등식은
θ 2 ( q ) 4 + θ 4 ( q ) 4 = θ 3 ( q ) 4 표시 스타일 \theta _{2}(q)^{4}+\theta _{4}(q)^{4}=\theta _{3}(q)^{4}} 또는 그와 동등하게,
ϑ 01 ( 0 ; τ ) 4 + ϑ 10 ( 0 ; τ ) 4 = ϑ 00 ( 0 ; τ ) 4 표시 스타일 \vartheta _{01}(0;\vartheta)^{4}+\vartheta _{10}(0;\vartheta)^{4}=\vartheta _{00}(0;\vartheta)^{4}}} 4도의 페르마 곡선입니다.
타원형 명사 세타 함수의 정의 및 동일성 자코비 함수는 타원 계수( τ ) displaystyle (\ )} displaystyle } 관점 τ displaystyle ' = k2 displaystyle displaysqrt {1-k^{2 시작 τ{\displaystyle \tau}
k ′ ( τ ) = 1 − k 2 = { θ 4 [ q ( k ) ] θ 3 [ q ( k ) ] } 2 {\displaystyle k'(\displaystyle k')=slotsqrt {1-k^{2}}=slotsbiggl \{\theta_{4}[q(k)] \over \theta_{3}[q(k)}{\biggr \}^{2}}}}} 첫 번째 종류 의 타원형 이름 과 완전한 타원 적분 을 정의합니다.
q ( k ) = 해외의 [ − π K ( 1 − k 2 ) K ( k ) ] = 해외의 [ − π K ′ ( k ) K ( k ) ] {\displaystyle q(k)=\exp {\biggl [}-\pi \,{\frac {K({\sqrt {1-k^{2}}}}{K(k)}}}{K(k)}}}=\exp {\frac {K(k)}}}} 타원 적분 K, 계수, nomq 함수 및 세타 함수 사이에는 다음과 같은 항등식이 존재합니다.
θ 3 [ q ( k ) ] = 2 π − 1 K ( k ) {\displaystyle \theta _{3}[q(k)]=sksqrt {2\pi ^{-1}K(k)}}} θ 4 [ q ( k ) ] = 1 − k 2 4 2 π − 1 K ( k ) {\displaystyle \theta _{4}[q(k)]=nbsqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi^{-1}K(k))}} θ 2 [ q ( k ) ] = k 1 / 2 2 π − 1 K ( k ) {\displaystyle \theta _{2}[q(k)]= k^{1/2}{\sqrt {2\pi ^{-1}K(k)}}} 첫 번째 종류의 완전한 타원 적분에 대한 두 가지 동일한 정의는 다음과 같습니다.
K ( k ) = ∫ 0 π / 2 1 1 − k 2 죄악 ( φ ) 2 ∂ φ {\displaystyle K(k)=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-k^{2}\sin(\varphi)^{2}}}\displaystyle \varphi} K ( k ) = π 2 ∑ a = 0 ∞ [ ( 2 a ) ! ] 2 16 a ( a ! ) 4 k 2 a {\displaystyle K(k)=displayfrac{pi}{2}}\sum _{a=0}^{\infty}{\frac{(2a)!] ^{2}}{16^{a}(a!) ^{4}}k^{2a}} 열을 사용하여 동일한 이름 함수 정의를 생성할 수 있습니다. 다음 함수는 다음과 같습니다.
1 − 1 − k 2 4 1 + 1 − k 2 4 = θ 3 [ q ( k ) ] − θ 4 [ q ( k ) ] θ 3 [ q ( k ) ] + θ 4 [ q ( k ) ] = [ ∑ n = 1 ∞ 2 q ( k ) ( 2 n − 1 ) 2 ] [ 1 + ∑ n = 1 ∞ 2 q ( k ) 4 n 2 ] − 1 표시({style\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}={theta_{3}[q(k)]-\theta_{4}[q(k)]}{\theta_{4}}{{4}}}}{\ta_{{{n^{n}}{n^2}{n^{n}}}}}}}}}}}{{{{n^ q 다음에 이 함수를 풀면 다음과 같은 결과를 얻을 수 있습니다[4] [5] [6]
q ( k ) = ∑ n = 1 ∞ 문장 부호 ( n ) 2 4 n − 3 ( 1 − 1 − k 2 4 1 + 1 − k 2 4 ) 4 n − 3 = [ ∑ n = 1 ∞ 문장 부호 ( n ) 2 4 n − 3 ( k 1 + 1 − k 2 ) 4 n − 3 ] 2 = k 2 { 1 2 + [ ∑ n = 1 ∞ 문장 부호 ( n + 1 ) 2 4 n + 1 k 2 n ] } 4 \displaystyle q(k)=\sum _{n=1}^{\infty}{\frac{\text{Sc}(n)}{2^{4n-3}}{\biggl(}){\frac{1-{\sqrt[{4}]{1-k^{2}}}{1+{\biggrtext}{{{n}{{n}}{n}{\text}{{{{{{n}}}}}}{{\text}}}}}{{{{{ 1}^{\infty}{\frac{\text{Sc}}(n+1)}{2^{4n+1}}k^{2n}{\biggr}}{\biggr \}}^{4}} q ( k ) = k 2 ( 1 2 + 2 32 k 2 + 15 512 k 4 + 150 8192 k 6 + 1707 131072 k 8 + … ) 4 표시 스타일 q(k)=k^2}{\bigl(}{\color {limegreen}{\frac {color {limegreen}{\frac {color {limegreen}{\frac}{\frac {color {limegreen}{\frac}{\frac {color {limegreen}}{{32}}k^2}+{\frac{\frac{2}k^{\frac{\frac{\frac{\color {{\color {\color 카를 하인리히 셸바흐는 그 의 작품 Die Lehre von denelliptischen Integralen und den Thetafunktionen 에서 이 수열의 파생을 60페이지 아래에 썼습니다. 그는 치환 계산을 통해 타원형의 네 번째 근의 계수를 알아냈습니다.
셸바흐 슈바르츠 수는 분자에 있고 16의 거듭제곱은 분모에 있습니다.
이와 관련하여 다음 제한이 유효합니다.
림 n → ∞ Sc(n) n = 16 {\displaystyle \lim _{n\to \infty}{\sqrt[{n}]{\text{Sc(n)}}}=16} 림 n → ∞ Sc(n + 1) Sc(n) = 16 {\displaystyle \lim _{n\to \infty}{\frac {text{Sc(n + 1)}}{\text{Sc(n)}}=16} 다음[7] [8]
Sc(1) Sc(2) Sc(3) Sc(4) Sc(5) Sc(6) Sc(7) Sc(8) 1 2 15 150 1707 20910 268616 3567400
타원 정수열 실레시아 독일 수학자 헤르만 아만두스 슈바르츠는 그뢰섹 장 에서 카를 하인리히 셸바흐에 의해 연구된 정수 수열을 묘사한 정수 수열에 대한 포멜른드 레르샤체줌 게브라우체 데엘립티셴 펑크티넨 을 그뢰섹 장에 썼습니다. 게다가 그의 셸바흐 슈바르츠 수열 Sc(n)는 20세기 수학자 카를 테오도르 빌헬름 바이어슈트라스 와 루이 멜빌 밀른-톰슨에 의해 분석되었습니다. 수학자 아돌프 크네서는 다음과 같은 패턴에 기초하여 이 수열에 대한 합성 방법을 결정했습니다.
문장 부호 ( n + 1 ) = 2 n ∑ m = 1 n 문장 부호 ( m ) Kn ( n + 1 − m ) {\style{text{Sc}(n+1)=sumfrac{2}{n}\sum_{m=1}^{n}{\text{Sc}}(m){\text{Kn}(n+1-m)}을(를) 표시합니다. 수학자 카를 하인리히 셸바흐 도 이 정수열 관계를 연구했고 그의 작품에서 그 는[9] 그것 을 자세히 다루었습니다 . Schellbach Schwarz 시퀀스 Sc(n)는 숫자 A002103 아래에 있는 숫자 시퀀스의 온라인 백과사전에 입력되고 Kn(n)은 숫자 A227503 아래에 입력됩니다. Kneser 정수 시퀀스 Kn(n)은 다음과 같은 방법으로 구성될 수 있습니다.
Kn ( 2 n ) = 2 4 n − 3 ( 4 n 2 n ) + ∑ m = 1 n 4 2 n − 2 m ( 4 n 2 n − 2 m ) Kn ( m ) {\style{text{Kn}}(2n)=2^{4n-3}{\binom {4n}{2n}}{\sum _{m=1}^{2n-2m}{\binom {4n}{2n-2m}{\text{Kn}}(m)}을(를 표시합니다.
Kn ( 2 n + 1 ) = 2 4 n − 1 ( 4 n + 2 2 n + 1 ) + ∑ m = 1 n 4 2 n − 2 m + 1 ( 4 n + 2 2 n − 2 m + 1 ) Kn ( m ) 표시({style{text{Kn}}(2n+1)=2^{4n-1}{\binom {4n+2n+1}}+\sum _{m=1}^{n}4^{2n-2m+1}{\binom {4n+2m+1}}{\text{Kn}(m)}(m)}
실행된 예:
Kn ( 2 ) = 2 × 6 + 1 × 1 = 13 표시{style{text{Kn}}(2)=2\times 6+1\times {color{cornflowerblue}1}=오렌지색 {cornflowerblue}13}
Kn ( 3 ) = 8 × 20 + 24 × 1 = 184 디스플레이 {style{text{Kn}(3)=8\times 20+24\times {color{cornflowerblue}1}=오렌지색 {cornflowerblue}}
Kn ( 4 ) = 32 × 70 + 448 × 1 + 1 × 13 = 2701 디스플레이 {style {text {Kn}(4)=32\times 70+448\times {color {cornflowerblue}1}+1\times {color {cornflowerblue}13}=color color {cornflowerblue}2701}
Kn ( 5 ) = 128 × 252 + 7680 × 1 + 40 × 13 = 40456 디스플레이 {style{text{Kn}}(5)=128\times252+7680\times{color{cornflowerblue}1}+40\times{color{cornflowerblue}13}=color{cornflowerblue}40456}
Kn ( 6 ) = 512 × 924 + 126720 × 1 + 1056 × 13 + 1 × 184 = 613720 표시{style{text{Kn}}(6)=color\times924+126720\times{color{cornflowerblue}1+1056\times{color{color{cornflowerblue}13}+1\times{color{color{colorflowerblue}13}+1\times}=color{color{color{color{color{color{
Kn ( 7 ) = 2048 × 3432 + 2050048 × 1 + 23296 × 13 + 56 × 184 = 9391936 디스플레이 {style{text{Kn}}(7)=2048\times 3432+2050048\times {color {cornflowerblue}1}+23296\times {color {color {cornflowerblue}13}+56\times {color {colorflowerblue}=color {color}9391936}
Kneser 시퀀스는 주기 비율(반주기 비율)의 Taylor 시리즈 에 나타납니다.
1 4 인 ( 16 x 2 ) − π K ′ ( x ) 4 K ( x ) = ∑ n = 1 ∞ Kn ( n ) 2 4 n − 1 n x 2 n 표시({style\frac{1}{4}}\frac{\frac{16}{x^{2}}}{\bigr}}-{\frac{pi \,K'(x)}{4\,K(x)}=\sum_{n=1}^{\infty}}{\frac{{n-1}}}}{2},\x^{n}}{n^2}}}{n^2}}}{n^2}}}. 1 4 인 ( 16 x 2 ) − π K ′ ( x ) 4 K ( x ) = 1 8 x 2 + 13 256 x 4 + 184 6144 x 6 + 2701 131072 x 8 + 40456 2621440 x 10 + … 표시({style{limegreen}{\frac{1}{4}}\ln{bigl(}{\frac{16}{x^{2}}}{\bigr)}-{\frac{pi \,K'(x)}{4\, K(x)}={frac{color{cornflowerblue}1}{8}}x^{2}+{\frac{color{cornflowerblue}13}{256}}x^{4}+{\frac{color{cornflowerblue}2701}{1372}}x{8}+{\frac{color{color{color{color{color{color{color{color{color{color{color{col x{displaystyle } 뒤 생성 함수를 보여주는 다음 방정식으로 이어집니다.
π 2 8 x ( 1 − x 2 ) K ( x ) 2 − 1 2 x = ∑ n = 1 ∞ Kn ( n ) 2 4 n − 2 x 2 n − 1 표시({style\frac{pi^{2}}{8x(1-x^{2})K(x)^{2}}-{\frac{1}{2x}}=\sum_{n=1}^{\infty}{\frac{\text{Kn}}}(n)}{2^{2n-1}}}x^{2n-1}}}}}. π 2 8 x ( 1 − x 2 ) K ( x ) 2 − 1 2 x = 1 4 x + 13 64 x 3 + 184 1024 x 5 + 2701 16384 x 7 + 40456 262144 x 9 + … 표시({style {color {\color {\pi ^{2}}{8x(1-x^{2})K(x)^{2}}-{\frac {{color {cornflower blue}{4}}x+{\frac {color {color {color {colorflower blue})x^{3}+{\frac {{x}{frac {{flower}{frac{flamor}{flamer}{fla}{frac{f 이 결과는 분자에서 Legendre의 관계 KE' EK 'K = 12 µ displaystyle \,E'+E\,K'-K\,K tftfrac{1}{2}}\pi}
다음 표에는 셸바흐 슈바르츠 수, 무릎 수, 아페리 수가 포함되어 있습니다.
구성된 시퀀스 Kneser 및 Schellbach Schwarz 색인 n Kn(n) (A227503) Sc(n) (A002103) 1 1 1 2 13 2 3 184 15 4 2701 150 5 40456 1707 6 613720 20910 7 9391936 268616 8 144644749 3567400
셸바흐 슈바르츠 수열에 대해 언급된 패턴 공식은 다음과 같습니다.
문장 부호 ( n + 1 ) = 2 n ∑ m = 1 n 문장 부호 ( m ) Kn ( n + 1 − m ) {\style{text{Sc}(n+1)=sumfrac{2}{n}\sum_{m=1}^{n}{\text{Sc}}(m){\text{Kn}(n+1-m)}을(를) 표시합니다. 다음에서는 셸바흐 슈바르츠 수가 연속적으로 구축되는 방법을 예로 들어 설명합니다. 이를 위해 숫자 Sc(4) = 150, Sc(5) = 1707 및 Sc(6) = 20910이 사용됩니다.
S c ( 4 ) = 2 3 ∑ m = 1 3 S c ( m ) K n ( 4 − m ) = 2 3 [ S c ( 1 ) K n ( 3 ) + S c ( 2 ) K n ( 2 ) + S c ( 3 ) K n ( 1 ) ] \displaystyle \mathrm {Sc}(4)={2}{3}}\sum _{m=1}^{3}\mathrm {Sc}(m)\mathrm {Kn}(4-m)={2}{\bigl}{\color {\color}\color {\color}\color{color}\color{color}{color}{color}{color}{color}{{{color}{color}{col {\color {cornflowerblue}\mathrm {Kn}(1)}{\bigr}}} S c ( 4 ) = 2 3 ( 1 × 184 + 2 × 13 + 15 × 1 ) = 150 표시({style{color{color{color{color}\mathrm{Sc}(4)}=colorfrac{2}{3}}{\bigl({color{color{cornflowerblue}{color}{color}{color{color}{color}{color}{color}{color{color}{color}{color}{color}{color}{color}{color}{col S c ( 5 ) = 2 4 ∑ m = 1 4 S c ( m ) K n ( 5 − m ) = 2 4 [ S c ( 1 ) K n ( 4 ) + S c ( 2 ) K n ( 3 ) + S c ( 3 ) K n ( 2 ) + S c ( 4 ) K n ( 1 ) ] \displaystyle \mathrm {Sc}(5)={2}{4}}\sum _{m=1}^{4}\mathrm {Sc}(m)\mathrm {Kn}(5-m)={2}{\bigl}{\color {\color}\color {color}\color{color}\kn}{{color}{\color}{\color}{\color}{\color}{{{\color}{\c lor {navy}\mathrm {Sc}(4)}\,{\color {cornflowerblue}\mathrm {Kn}(1)}{\bigr}}}} S c ( 5 ) = 2 4 ( 1 × 2701 + 2 × 184 + 15 × 13 + 150 × 1 ) = 1707 표시({style{color{color{color}\mathrm{Sc}(5)}=colorfrac{2}{4}}{\bigl(}{color{color{color{cornflowerbluor})1}{\color{color{colorflowerbluor}2}\times{{{color{color}{color{color{color{color{color{color}}}\color{color S c ( 6 ) = 2 5 ∑ m = 1 5 S c ( m ) K n ( 6 − m ) = 2 5 [ S c ( 1 ) K n ( 5 ) + S c ( 2 ) K n ( 4 ) + S c ( 3 ) K n ( 3 ) + S c ( 4 ) K n ( 2 ) + S c ( 5 ) K n ( 1 ) ] \displaystyle \mathrm {Sc}(6)={2}{5}}\sum _{m=1}^{5}\mathrm {Sc}(m)\mathrm {Kn}(6-m)={2}{\bigl}{\color {\color}\color{color}\color{color}\color{color{color}{color}{color}{color}{color}{{color}{color}{ lor {navy}\mathrm {Sc}(4)}\,{\color {cornflowerblue}\mathrm {Kn}(2)}+{\color {navy}\mathrm {Sc}(5)},{\color {cornflowerblue}\mathr}}} S c ( 6 ) = 2 5 ( 1 × 40456 + 2 × 2701 + 15 × 184 + 150 × 13 + 1707 × 1 ) = 20910 표시({style {color {color}\mathrm {Sc}(6)}=colorfrac {2}{5}}{\bigl({color{colorflowerblue}{color}{color{color}{colorflowerblue}{color}{color}{color}{color{color{color}{color}{color}{color}{color}{\color{color}{color 또는 {{delay}(으)로 10}}. 자코비 항등식 Jacobi의 ID는 τ↦ + 1 및 τ↦ -.mw-parser-output .sfrac{white-space:nowrap}mw-parser-output .sfrac.tision {display:inline-block; 수직-align:0.5em; font-size:85%; text-center:align-nummwa-out.parac-outparac-outparac-out.mw.mwmwmwmwmw.mw.mw.mw.mwut.sfrac.den{display:block; line-height:1em; line-height:1em; mw-parser-output.sr-only{border-top:1den{border-top:1den}{border:0,0,0,0); 높이:1parser-output.sr-only{border:0;border:1}{border:0;mworder:0}.sr-only{border:0;mworder:0. 지수에서 1 을 τ에 추가하면 1/ 2 z 에 추가 n 2 mod 2). 두 번째로,
α의 = ( − i τ ) 1 2 해외의 ( π τ i z 2 ) . {\displaystyle \alpha = alpha\lambda )^{\frac {1}{2}}\exp \leftpi\frac {pi}}iz^{2}\right}{2}\right} 그리고나서
ϑ 00 ( z τ ; − 1 τ ) = α의 ϑ 00 ( z ; τ ) ϑ 01 ( z τ ; − 1 τ ) = α의 ϑ 10 ( z ; τ ) ϑ 10 ( z τ ; − 1 τ ) = α의 ϑ 01 ( z ; τ ) ϑ 11 ( z τ ; − 1 τ ) = − i α의 ϑ 11 ( z ; τ ) . display {style {aligned}\vartetha _{00}\! \leftpx\frac {z}{\frac {\frac {-1}{\frac }};\right)&=\alpha \,\vartheta _{00}(z;\bartheta)\bartheta &\vartheta _{01}\! \leftpx\frac {z}{\frac {\frac {-1}{\frac }\right)&=\alpha \,\vartheta _{10}(z;\deta)\[3pt]\vartheta _{10}\! \leftpx\frac{z}{\frac{\frac}};{\frac{-1}{\frac}}\right)&=\alpha \,\vartheta_{01}(z;\fartheta)\bartheta &\vartheta_{11}\! \leftpx\frac {z}{\frac {\frac}};{\frac {-1}{\frac }\right)&=-i\alpha \,\vartheta_{11}(z;\fartheta). \end{aligned}}} 세타는 이름 측면에서 기능합니다. 세타 함수를 z와 π 로 표현하는 대신 인수 w와 nomeq 로 표현할 수 있습니다. 여기 e πiz 및 q πiτ 이 형태에서, 함수들은 다음과 같습니다.
ϑ 00 ( w , q ) = ∑ n = − ∞ ∞ ( w 2 ) n q n 2 ϑ 01 ( w , q ) = ∑ n = − ∞ ∞ ( − 1 ) n ( w 2 ) n q n 2 ϑ 10 ( w , q ) = ∑ n = − ∞ ∞ ( w 2 ) n + 1 2 q ( n + 1 2 ) 2 ϑ 11 ( w , q ) = i ∑ n = − ∞ ∞ ( − 1 ) n ( w 2 ) n + 1 2 q ( n + 1 2 ) 2 . 표시(\style{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty}^{\left(w^{2}\right)^{n}q^{n^{2}}\deta &\vartheta _{{n=-\infty}(w,q)&\sum _{n}\ta^{n}{n}{ta}{ta^{n^{ta}{n^{ta}{n^{n^{n^{n} ^{n+{\frac{1}{2}}}q^{\left(n+{\frac{1}{2}}\right)^{2}}\colon &\vartheta_{11}(w,q)&=i\sum_{n=-\infty}^{n}(w^{2}\right) ^{n+{\frac {1}{2}}q^{\left(n+{\frac {1}{2}}\right)^{2}}. \end{aligned}}} 우리는 세타 함수가 지수 함수에 대한 직접적인 참조 없이 w와 q 측면 에서도 정의될 수 있다는 것을 알 수 있습니다. 따라서 이러한 공식은 p-adic 숫자 필드와 같이 지수 함수가 모든 곳에서 정의되지 않을 수 있는 다른 필드에 대해 Theta 함수를 정의하는 데 사용될 수 있습니다.
제품 표현 자코비 삼중곱 (Macdonald 동일성의 특별한 경우)은 q < 1 w ≠ 0 을 갖는 복소수 w 와 q에 대해 다음과 같이 말합니다.
∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + w 2 q 2 m − 1 ) ( 1 + w − 2 q 2 m − 1 ) = ∑ n = − ∞ ∞ w 2 n q n 2 . \displaystyle \displaystyle \displaystyle \displaystyle _{m=1}^{\infty}\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum_{n=\infty}w^{n}^{n}^{n}^{n^{n^{2}}}}. 예를 들어, 그것은 하디와 라이트 이론 입문
세타 함수를 name q πiτ = e로 표현하면(일부 저자는 q 2πiτ 대신 w πiz 취합니다
ϑ ( z ; τ ) = ∑ n = − ∞ ∞ 해외의 ( π i τ n 2 ) 해외의 ( 2 π i z n ) = ∑ n = − ∞ ∞ w 2 n q n 2 . {\displaystyle \vartheta (z;\infty)=\sum _{n=-\infty}^{\infty}\exp(\pii\infty)=\sum _{n=-\infty}^{\infty}w^{2n}^{n^{2}}}. 따라서 우리는 형태의 세타 함수에 대한 곱 공식을 얻습니다.
ϑ ( z ; τ ) = ∏ m = 1 ∞ ( 1 − 해외의 ( 2 m π i τ ) ) ( 1 + 해외의 ( ( 2 m − 1 ) π i τ + 2 π i z ) ) ( 1 + 해외의 ( ( 2 m − 1 ) π i τ − 2 π i z ) ) . 디스플레이 스타일 \vartheta (z;\displaystyle)=\big _{m=1}^{\infty}{\big(}1-\exp(2m\pii\big)}{\big(}1+\exp{\big(2m-1)\pi\big()}{\big(1+\bigi\bigi\big)}}{\big(1}{\big(1}\big(1}\big)}\big(1}. w 및 q 측면 에서:
ϑ ( z ; τ ) = ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + q 2 m − 1 w 2 ) ( 1 + q 2 m − 1 w 2 ) = ( q 2 ; q 2 ) ∞ ( − w 2 q ; q 2 ) ∞ ( − q w 2 ; q 2 ) ∞ = ( q 2 ; q 2 ) ∞ θ ( − w 2 q ; q 2 ) 표시({style{aligned}\vartheta(z;\baseta)&=\baseta_{m=1}^{\infty}\left(1+q^{2m-1}w^{2}\right)\left(1+{\frac{q^{2m-1}}{w^{2}}}\right) \\&=\left(q^{2};q^{2}\right)_{\infty}\,\left(\)w^{2}\right}_{\infty}\,\left(\frac{q}{w^{2}}}};q^{2}\infty}\left(q^{2}){\ta}\lefty}\left(\left)\left(\right)\right^{\ta){\ta}\ta}\left)\lefty 여기서 ( ∞ ; )는 q-Pochhammer 기호이고 γ ( ; )는 q-theta 함수입니다. 용어를 확장하면 자코비 트리플 제품도 작성할 수 있습니다.
∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + ( w 2 + w − 2 ) q 2 m − 1 + q 4 m − 2 ) , \"표시 스타일 \displaystyle \displaystyle _{m=1}^{\infty}\left(1-q^{2m}\right){\Big(}1+\left(w^{2}+w^{-2}\right)q^{2m-1}+q^{4m-2}{\Big)}}, 우리가 또한 쓸 수 있는 것은.
ϑ ( z ∣ q ) = ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + 2 코스 ( 2 π z ) q 2 m − 1 + q 4 m − 2 ) . {\displaystyle \vartheta (z\mid q)=\display_{m=1}^{\infty}\left(1+2\cos(2\piz)^{2m-1}+q^{4m-2}\right)} 이 형식은 일반적으로 유효하지만 z가 실제일 때 는 특히 중요합니다. 보조 세타 함수에 대한 유사한 제품 공식은 다음과 같습니다.
ϑ 01 ( z ∣ q ) = ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 − 2 코스 ( 2 π z ) q 2 m − 1 + q 4 m − 2 ) , ϑ 10 ( z ∣ q ) = 2 q 1 4 코스 ( π z ) ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 + 2 코스 ( 2 π z ) q 2 m + q 4 m ) , ϑ 11 ( z ∣ q ) = − 2 q 1 4 죄악 ( π z ) ∏ m = 1 ∞ ( 1 − q 2 m ) ( 1 − 2 코스 ( 2 π z ) q 2 m + q 4 m ) . 표시(\style{aligned}\vartheta _{01}(z\mid q)&=\cisco _{m=1}^{\infty}\left(1-q^{2m}\right)\left(1-2\cos(2\piz) q^{2m-1}+q^{3pt}\vartheta _{10(z\mid q)={cos}{\cos}{\cos}{\cos}{\ft}{\cos}{\cos} \\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac{1}{4}}\sin(\piz)\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\piz)q}+q^{4m}\right). \end{aligned}}} 특히,
림 q → 0 ϑ 10 ( z ∣ q ) 2 q 1 4 = 코스 ( π z ) , 림 q → 0 − ϑ 11 ( z ∣ q ) 2 q − 1 4 = 죄악 ( π z ) \displaystyle \lim _{q\to 0}{\frac \vartheta _{10}(z\mid q)}{2q^{\frac {1}{4}}}=\cos(\piz),\lim \lim \to 0}{q\to 0}{\frac {11}(z\mid q})}{2q^{-{{\frac {\frac {\pi}}=\pi}\pi}\pi}\pi} 그래서 우리는 그것들을 주기 함수 , cos displaystyle \sin,\cos
적분 표현 자코비 세타 함수는 다음과 같은 적분 표현을 갖습니다.
ϑ 00 ( z ; τ ) = − i ∫ i − ∞ i + ∞ e i π τ u 2 코스 ( 2 π u z + π u ) 죄악 ( π u ) d u ; ϑ 01 ( z ; τ ) = − i ∫ i − ∞ i + ∞ e i π τ u 2 코스 ( 2 π u z ) 죄악 ( π u ) d u ; ϑ 10 ( z ; τ ) = − i e i π z + 1 4 i π τ ∫ i − ∞ i + ∞ e i π τ u 2 코스 ( 2 π u z + π u + π τ u ) 죄악 ( π u ) d u ; ϑ 11 ( z ; τ ) = e i π z + 1 4 i π τ ∫ i − ∞ i + ∞ e i π τ u 2 코스 ( 2 π u z + π τ u ) 죄악 ( π u ) d u . 표시(\style{aligned}\vartheta _{00}(z;\filename)&=-i\int_{i-\infty}^{i\pi \pi \pi u^{2}}{\frac{cos(2\piu)}{\pi(\piu)}{\pta{\varta{z};\in}\infty}\in^{i}\in^i}\infty}\in^i}\in^{i}\fty. }{\sin(\piu)}\mathrm {d}u;\[6pt]\vartheta _{10}(z;\pi)&=-ie^{i\piz+{\frac{1}}i\pi \infty}^{i+\infty}^{i-\pi\pi\pi\fracu^2}{\mathpi\pi}\pi\pi\pi\pi\pi\pi\pi\pi\pi\pi\pi(2\piu) z+\pi \pi u)}{\sin(\pi u)}\mathrm {d} u.\end{aligned}}} 세타 Nullwert 함수 θ q ) displaystyle \theta_{3}(q)}
θ 3 ( q ) = 1 + 4 q 인 ( 1 / q ) π ∫ 0 ∞ 해외의 [ − 인 ( 1 / q ) x 2 ] { 1 − q 2 코스 [ 2 인 ( 1 / q ) x ] } 1 − 2 q 2 코스 [ 2 인 ( 1 / q ) x ] + q 4 d x 표시 스타일 \theta _{3}(q)=1+{\frac {4q{sq}{{pi}}}{\int_{0}^{\infty}{\frac \exp[-\fac(1/q)\,x^{2}\cos[2-q^(1/q),x]}{1-2q{q}{2}{\math^{\cos}}{\cos}{2}{\x}{\x}\cos}{\x}\x}\x}\x}\cos} 이 공식은 애틀랜타의 조지아 출신 수학자 맥시 슈미트에 의해 함수 변환을 생성하는 에세이 스퀘어 시리즈 에서 논의되었습니다.
이 공식을 기반으로 다음과 같은 세 가지 저명한 예가 제공됩니다.
[ 2 π K ( 1 2 2 ) ] 1 / 2 = θ 3 [ 해외의 ( − π ) ] = 1 + 4 해외의 ( − π ) ∫ 0 ∞ 해외의 ( − π x 2 ) [ 1 − 해외의 ( − 2 π ) 코스 ( 2 π x ) ] 1 − 2 해외의 ( − 2 π ) 코스 ( 2 π x ) + 해외의 ( − 4 π ) d x 표시(\style\bigl [}{\frac {2}{\pi })K{\bigl (}{\frac {1}{2}}{\bigr}}{\bigr}}^{1/2}=\theta_{3}{\bigl[}\expigr}{\bigr}}{\inftypi}{\cos}x2}{{\cos}{\cos}{\cos}{\cos}{\cos}{\cos}{\pi^{\ [ 2 π K ( 2 − 1 ) ] 1 / 2 = θ 3 [ 해외의 ( − 2 π ) ] = 1 + 4 2 4 해외의 ( − 2 π ) ∫ 0 ∞ 해외의 ( − 2 π x 2 ) [ 1 − 해외의 ( − 2 2 π ) 코스 ( 2 2 π x ) ] 1 − 2 해외의 ( − 2 2 π ) 코스 ( 2 2 π x ) + 해외의 ( − 4 2 π ) d x 표시(\style{\frac{2}{\pi })K({\sqrt{2}}-1){\bigr}}^{1/2}=\theta_{3}{\bigl[}\exp{\sqrt{2}}\bigr}=1+4,{\sqrt{\sqrt{2}}{\pi}{\pi}{\pi}{\pi}{\pi}{\pi}{\pi}{\pi}{\pi} rt {2}}\,\pi)}\,\mathrm {d} x} { 2 π K [ 죄악 ( π 12 ) ] } 1 / 2 = θ 3 [ 해외의 ( − 3 π ) ] = 1 + 4 3 4 해외의 ( − 3 π ) ∫ 0 ∞ 해외의 ( − 3 π x 2 ) [ 1 − 해외의 ( − 2 3 π ) 코스 ( 2 3 π x ) ] 1 − 2 해외의 ( − 2 3 π ) 코스 ( 2 3 π x ) + 해외의 ( − 4 3 π ) d x 표시(\style\bigl \{}{\frac {2}{\pi }K{\bigl [}\bigl (}{\frac \pi }{12}}{\bigr}}{\bigr}{\bigr}}{\bigr}{\bigr}}{\bigl [}\exp{\sqrta{\sqrtrt}}{\pi}}{\bigl}{\bigl}{\bigl}{\bigl}{\bigl }}\,\pi)\cos(2"sqrt {3}}\,\pi)+\exp(-4"sqrt {3}}}\,\mathrm {d} x} 또한 세타 예제 θ 12 ) displaystyle \theta {3}({\tfrac {1}{2}}) θ 13 ) displaystyle \theta {3}({\tfrac {1}{3}})}
θ 3 ( 1 2 ) = 1 + 2 ∑ n = 1 ∞ 1 2 n 2 = 1 + 2 π − 1 / 2 인 ( 2 ) ∫ 0 ∞ 해외의 [ − 인 ( 2 ) x 2 ] { 16 − 4 코스 [ 2 인 ( 2 ) x ] } 17 − 8 코스 [ 2 인 ( 2 ) x ] d x 표시 스타일 \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{2^{n^{2}}=1+2\pi ^{1/2}{\infty}{\infty}{\frac{{{\expi}{{{{\x}}{\x}{\x}{\cos}{\x}{\cos}{\cos}{\ θ 3 ( 1 2 ) = 2.128936827211877158669 … {\displaystyle \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=2.128936827211877158669\ldots} θ 3 ( 1 3 ) = 1 + 2 ∑ n = 1 ∞ 1 3 n 2 = 1 + 4 3 π − 1 / 2 인 ( 3 ) ∫ 0 ∞ 해외의 [ − 인 ( 3 ) x 2 ] { 81 − 9 코스 [ 2 인 ( 3 ) x ] } 82 − 18 코스 [ 2 인 ( 3 ) x ] d x 표시 스타일 \theta _{3}{\frac {1}{3}}{\bigr}=1+2\sum _{n=1}^{\infty}{\frac {1}{3^{n^{2}}=1+{\frac {4}{3}\pi ^{-1/2}{\int{{{}\infty}{{{\cos}\cos}\cos}{{{\x}\cos}{{{{\bigrt}\cos}{\cos}{\cos θ 3 ( 1 3 ) = 1.691459681681715341348 … {\displaystyle \theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1.691459681681715341348\ldots} 명시적 값 이러한 결과의 대부분에 대한 적절한 신용은 라마누잔에게 돌아옵니다. 라마누잔의 잃어버린 노트와 오일러 함수의 관련 참조를 참조하십시오.오일러 함수에 인용 된 라마누잔 결과와 몇 가지 기본 연산을 통해 아래의 결과를 얻을 수 있으므로 라마누잔의 잃어버린 노트에 있거나 바로 그 결과를 따릅니다.Yi(2004)[10] 정의,
φ ( q ) = ϑ 00 ( 0 ; τ ) = θ 3 ( 0 ; q ) = ∑ n = − ∞ ∞ q n 2 \displaystyle \varphi (q)=\vartheta _{00}(0;\vartheta)=\theta _{3}(0;q)=\sum _{n=-\infty}^{\infty}q^{n^{2}}}}} q = e π i , displaystyle q e^{\piii\ }, = n , displaystyle \n {\ sqrt 1}, Dedekinde eta 함수 τ 그런 = 1 2 , , displaystyle 1, 2, 3, displaystyle }) 대해
φ ( e − π ) = π 4 Γ ( 3 4 ) = 2 η ( − 1 ) φ ( e − 2 π ) = π 4 Γ ( 3 4 ) 2 + 2 2 φ ( e − 3 π ) = π 4 Γ ( 3 4 ) 1 + 3 108 8 φ ( e − 4 π ) = π 4 Γ ( 3 4 ) 2 + 8 4 4 φ ( e − 5 π ) = π 4 Γ ( 3 4 ) 2 + 5 5 φ ( e − 6 π ) = π 4 Γ ( 3 4 ) 1 4 + 3 4 + 4 4 + 9 4 12 3 8 φ ( e − 7 π ) = π 4 Γ ( 3 4 ) 13 + 7 + 7 + 3 7 14 3 8 ⋅ 7 16 φ ( e − 8 π ) = π 4 Γ ( 3 4 ) 2 + 2 + 128 8 4 φ ( e − 9 π ) = π 4 Γ ( 3 4 ) 1 + 2 + 2 3 3 3 φ ( e − 10 π ) = π 4 Γ ( 3 4 ) 64 4 + 80 4 + 81 4 + 100 4 200 4 φ ( e − 11 π ) = π 4 Γ ( 3 4 ) 4 + 11 − 3 3 황갈색의 ( 1 4 아코시 ( 7 4 ) + 1 6 아르탄 ( 27 47 3 ) ) 44 8 ⋅ − 66 + 22 11 φ ( e − 12 π ) = π 4 Γ ( 3 4 ) 1 4 + 2 4 + 3 4 + 4 4 + 9 4 + 18 4 + 24 4 2 108 8 φ ( e − 13 π ) = π 4 Γ ( 3 4 ) − 1 13 + 2 13 3 코트 ( 1 6 아르탄 ( 6 11 3 ) ) φ ( e − 14 π ) = π 4 Γ ( 3 4 ) 13 + 7 + 7 + 3 7 + 10 + 2 7 + 28 8 4 + 7 28 7 16 φ ( e − 15 π ) = π 4 Γ ( 3 4 ) 7 + 3 3 + 5 + 15 + 60 4 + 1500 4 12 3 8 ⋅ 5 2 φ ( e − 16 π ) = φ ( e − 4 π ) + π 4 Γ ( 3 4 ) 1 + 2 4 128 16 φ ( e − 17 π ) = π 4 Γ ( 3 4 ) 2 ( 1 + 17 4 ) + 17 8 5 + 17 17 + 17 17 2 φ ( e − 20 π ) = φ ( e − 5 π ) + π 4 Γ ( 3 4 ) 3 + 2 5 4 5 2 6 φ ( e − 36 π ) = 3 φ ( e − 9 π ) + 2 φ ( e − 4 π ) − φ ( e − π ) + π 4 Γ ( 3 4 ) 2 4 + 18 4 + 216 4 3 표시({style{aligned}\varphi \left(e^{-\pi}\right)&=displayfrac{sqrt[{4}}{\pi}}{\Gamma \leftfrac{3}{4}}\right) }}=nbsqrt {2}}\, \eta \left\sqrt {-1}\right)\\\varphi \left(e^{-2\pi}\right)&=sqfrac {\pi}{\Gamma \left\frac {3}{4}}}{\varphi \left(e^-3\pi}}{\frac}}{\frac{\frac\frac\frac\frac\frac\gamma}{\right}\frac\frac\frac\frac\frac\fracp;=nbfrac{ sqrt[{4}]{\pi }}{\Gamma \left\frac {3}{4}}}{\right)}{\frac {2+{\sqrt[{4}}}{4}}\\\varphi \left(e^{-5\pi}\right)&=frac {\gamma \left\frac{3}}{4}\right) }}{\sqrt{\frac{2+{\sqrt{5}}}{5}}\\\varphi \left(e^{-6\pi}\right)&={\pi}{\Gamma \left\frac{3}{4}}}}}{{\frac{\sqrt{4}}{\sqrt}{4}{\rt}{\rt}{\rt}{\rt}{\rt}}}{\varpi}{\rtrt {{\s} qrt {13+{\sqrt {7}}}+{\sqrt {7}}}{\sqrt[{8}]{14^{3}}}\cdot {{sqrt[{16}}}}\\\varphi \left(e^{-8\pi})&=frac{\gamma\rt\frt\frac{2}{\rt}{\rt}{\rt{\rt}{\rt}{\rt}{\rt}{\r\frac {1} +{\sqrt[{3}}}{2+2\sqrt{3}}}{3}}\\\varphi \left(e^{-10\pi}\right)&={\frac{sqrt}{\Gamma \left\frac{3}{4}}}{\frac{\sqrt}}{{\sqrt}{{{\sqrt}{{{{{{\sqrt}}}}}}{{\rt}{{\rt}{\ {4+{\sqrt {11}}-3"tfrac{3}}\tanh \left\tfrac{1}{4}}\operatorname{arcosh}\left\tfrac{7}{4}}\right)+{\tfrac{1}{6}\operatorname{artanh}\tfrac{27}{47}{\sqrtfrac{3}\right)\right)\right)} }{{\sqrt[{8}]{44}}\cdot{\sqrt{-66+22\sqrt{11}}}}\\\varphi \left(e^{-12\pi}\right)&={\Gamma \left\frac{3}}}{\frac{\sqrt}{\sqrt}{4}{{\rt}{\rt}{4}{{\rt}{\rt}{\rt}{\rt}{\rt경주하다 qrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right) }}{\sqrt {-{\tfrac {1}{13}}+{\tfrac {2}{13}}{\sqrt {3}}{\cot \left\tfrac {1}{6}}\operator 이름 {artanh} \tfrac {6}{11}{\sqrtfrac {3}}\right)\right) }}\\\varphi \left(e^{-14\pi}\right)&=sqfrac{sqrt}{\pi}}{\Gamma \left\frac{3}{4}}}}{\fracsqrt {13+{\sqrt{7}}}}}{\sqrt{\sqrt{\sqrt}}}{\sqrt{\sqrt{\sqrt}}}{{\sqrt{\sqrt}} {3}{4}}\right )}{\frac{\sqrt{7+3\sqrt{3}}+{\sqrt{5}}+{\sqrt[{4}}}{{\sqrt[{4}}}}{{\sqrt[{8}}}}{{\cdot{{{5}}}}{\varphi}{\cdot{(e^{16\pi}\pi}\varphi})}\rt{\varphi}{\pi}{\frac{\pi }\rig ht)&=sqrt{\pi}{\Gamma \left\frac{3}{4}}}{\right}}{\frac{\sqrt{2}}(1+{\sqrt[{4}}{17}}}}{\sqrt{5+{\sqrt{17}}}}}{\sqrt{\sqrt{\pi}{\varrt{\va}{\var}\var}{\va}\var}\va}\var }}{\sqrt{\frac{3+2\sqrt[{4}}{5}}}}{5\varpi \left(e^{-36\pi}\right)&=3\varpi \left(e^{-9\pi}\right)+2\varpi \left(e^{-4\gamma}\right){\frac{\frac}}\frac{\frac{\rta}\rta}\rta}\frac{\rta }}{\sqrt[{3}]{{\sqrt[{4}}{2}}}+{\sqrt[{4}}}}+{\sqrt[{4}}}}{\end{aligned}}}}}} 겔폰드 상수의 역수가 홀수의 역수의 거듭제곱으로 증가하면 해당하는 ϑ 00 ({{{\ displaystyle \vartheta_{00}}) ({{displaystyle \phi}) 쌍곡선 렘니스카틱 사인을 사용하여 단순화된 방법으로 나타낼 수 있습니다.
φ [ 해외의 ( − 1 5 π ) ] = π 4 Γ ( 3 4 ) − 1 흐물흐 ( 1 5 2 ϖ ) 흐물흐 ( 2 5 2 ϖ ) 표시 스타일 \varphi \varphi \tfrac {1}{5}\pi ){\bigr ]}=slsqrt[{4}]{\pi }\,{\Gamma \left\tfrac {3}{4}}}^{-1}\operatorname {sqrt}{\rt}{\varfrac}{\bigrt}{\bigrt}{\va}{\bigrt}{\va}{\bi}{\b}{\bi}{\ φ [ 해외의 ( − 1 7 π ) ] = π 4 Γ ( 3 4 ) − 1 흐물흐 ( 1 7 2 ϖ ) 흐물흐 ( 2 7 2 ϖ ) 흐물흐 ( 3 7 2 ϖ ) 표시 스타일 \varphi \varphi \tfrac {1}{7}\pi ){\bigr ]}=slsqrt[{4}]{\pi }\,{\Gamma \left\tfrac {3}{4}}^{-1}\operatorname {sqrt}{\rt}{\bigrt}{\varc}{\bigrt}{\bigrt}{\va}{\bi}{\va}{\va}{\bi}{rt φ [ 해외의 ( − 1 9 π ) ] = π 4 Γ ( 3 4 ) − 1 흐물흐 ( 1 9 2 ϖ ) 흐물흐 ( 2 9 2 ϖ ) 흐물흐 ( 3 9 2 ϖ ) 흐물흐 ( 4 9 2 ϖ ) 표시 스타일 \varphi \varphi \tfrac {1}{9}\pi ){\bigr ]}=slsqrt[{4}]{\pi }\,{\Gamma \left\tfrac {3}{4}}}^{-1}\operatorname {sqrt}{\rtfrac}{2}{\bigrt}{\bigrt}{\bigrt}{\va}{\bi}{\bi}{rt}{\bi}{rt} 연산자 이름 {slh}{\tfrac {4}{9}{\sqrt {2}},\varpi{bigr}} φ [ 해외의 ( − 1 11 π ) ] = π 4 Γ ( 3 4 ) − 1 흐물흐 ( 1 11 2 ϖ ) 흐물흐 ( 2 11 2 ϖ ) 흐물흐 ( 3 11 2 ϖ ) 흐물흐 ( 4 11 2 ϖ ) 흐물흐 ( 5 11 2 ϖ ) 표시 스타일 \varphi \varphi \tfrac {1}{11}\pi ){\bigr ]}=slsqrt[{4}]{\pi }\,{\Gamma \left\tfrac {3}{4}}^{-1}\operatorname {sqrt}{{\rtfrac}}{\bigrt}{\bigrt}{\va}{\varc}{\bigrt}{\va}{\va}{\bi}{rt} )}\operatorname{slh}{bigl(}{\tfrac{4}{11}}{\sqrt{2}}{\varpi{bigr}}\operatorname{slh}{{\tfrac{5}}{\sqrt{2}}},\varpi{bigr}}}} 문자 displaystyle \varpi}) 렘니스케이트 상수를 나타냅니다.
다음과 같은 모듈식 ID가 유지됩니다.
2 φ ( q 4 ) = φ ( q ) + 2 φ 2 ( q 2 ) − φ 2 ( q ) 3 φ ( q 9 ) = φ ( q ) + 9 φ 4 ( q 3 ) φ ( q ) − φ 3 ( q ) 3 5 φ ( q 25 ) = φ ( q 5 ) 요람 ( 1 2 아크탄 ( 2 5 φ ( q ) φ ( q 5 ) φ 2 ( q ) − φ 2 ( q 5 ) 1 + s ( q ) − s 2 ( q ) s ( q ) ) ) 표시({style{aligned}2\varphi \left(q^{4}\right)&=\varphi(q)+{\sqrt{2}\left(q^{2}\right)-\varphi \left(q^{9}\right)&=\varphi(q)+\varphi(right)\fright(\fright)\varphi(\varphi)\varphi(\varphi)\varphi)\frac {1}{2}}\ Arctan \left\frac {2}{\sqrt {5}}{\frac \varphi \left(q^{5}\right)}{\varphi ^{2}(q)-\varphi ^{2}\left(q^{5}\right)}}{\frac {1+s(q)-s^{2}(q)}}\right)\right}{right}}}}}{end. 여기 q = s e π = eπ 5 τ displaystyle (q s\ (e^{\pii\ }\right R\left(-e^{-\pii/(5\ )) 로저스-라마누잔 연속 분수입니다.
s ( q ) = 황갈색의 ( 1 2 아크탄 ( 5 2 φ 2 ( q 5 ) φ 2 ( q ) − 1 2 ) ) 요람 2 ( 1 2 아크코트 ( 5 2 φ 2 ( q 5 ) φ 2 ( q ) − 1 2 ) ) 5 = e − π i / ( 25 τ ) 1 − e − π i / ( 5 τ ) 1 + e − 2 π i / ( 5 τ ) 1 − ⋱ 표시({style{aligned}s(q)&=skrt[{5}]{\tan \leftsqrt}{\frac{2}}\arctan \left\frac{2}}{\varphi ^{2}\right)}{\varphi ^{2}}-{\varphi ^{1}{\right}\cota}{\frac}{frac}{\frac}{frac}{frac}{frac}{\operat}{\frac}{ }}\\&=dddots {e^{-\pi i/(25\dots)}}{1-{\dots}{1+{\dots}}{1+{\dots {e^{-2\pi i/(5\dots)}}}}{\end{}}}}}}}{{{{\dots}}}}}}}}}}}{{{{{\end{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 수학자 브루스 베른트는 세타 함수의 추가[11]
φ ( 해외의 ( − 3 π ) ) = π − 1 Γ ( 4 3 ) 3 / 2 2 − 2 / 3 3 13 / 8 φ ( 해외의 ( − 2 3 π ) ) = π − 1 Γ ( 4 3 ) 3 / 2 2 − 2 / 3 3 13 / 8 코스 ( 1 24 π ) φ ( 해외의 ( − 3 3 π ) ) = π − 1 Γ ( 4 3 ) 3 / 2 2 − 2 / 3 3 7 / 8 ( 2 3 + 1 ) φ ( 해외의 ( − 4 3 π ) ) = π − 1 Γ ( 4 3 ) 3 / 2 2 − 5 / 3 3 13 / 8 ( 1 + 코스 ( 1 12 π ) ) φ ( 해외의 ( − 5 3 π ) ) = π − 1 Γ ( 4 3 ) 3 / 2 2 − 2 / 3 3 5 / 8 죄악 ( 1 5 π ) ( 2 5 100 3 + 2 5 10 3 + 3 5 5 + 1 ) 표시(\style{array}{lll}\varphi \left(\expx{\sqrt {3}},\pi)\right)&=&\pi ^{-1}{\Gamma \left\tfrac {4}{3}\right)}^{3/2}\varphi \left(\expx2sqright){\gamma\pi}{\pi}{\fradi}{\pi}\pi}{\pi}\pi,\pi)\right)&=&\pi ^{-1}{\Gamma \left\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{7/8}({\sqrt[{3}]{2}})\\\\varphi \left(\exp(-4\pi)\right)\gamma \left\tfrac {\frac}{3}{3}{3}{3}{3}{3}{3}{3}\right}^{3}{3}{3}{ \pi)\right)&=&\pi ^{-1}{\Gamma \leftfrac\tfrac{4}{3}}\right)}^{3/2}^{-2/3}}^{5/8}\sin\tfrac{2}{5}}}({\sqrtfrac{3}{2}}}{\tfrac{5}{\rtfrac}{3}{\rt}{3}{\rtfrac{\rt}}}{\rt}}{{{{{ 추가 값 세타[12]
φ ( 해외의 ( − 2 π ) ) = π − 1 / 2 Γ ( 9 8 ) Γ ( 5 4 ) − 1 / 2 2 7 / 8 φ ( 해외의 ( − 2 2 π ) ) = π − 1 / 2 Γ ( 9 8 ) Γ ( 5 4 ) − 1 / 2 2 1 / 8 ( 1 + 2 − 1 ) φ ( 해외의 ( − 3 2 π ) ) = π − 1 / 2 Γ ( 9 8 ) Γ ( 5 4 ) − 1 / 2 2 3 / 8 3 − 1 / 2 ( 3 + 1 ) 황갈색의 ( 5 24 π ) φ ( 해외의 ( − 4 2 π ) ) = π − 1 / 2 Γ ( 9 8 ) Γ ( 5 4 ) − 1 / 2 2 − 1 / 8 ( 1 + 2 2 − 2 4 ) φ ( 해외의 ( − 5 2 π ) ) = π − 1 / 2 Γ ( 9 8 ) Γ ( 5 4 ) − 1 / 2 2 15 / 8 ⋅ ( 1 5 3 코스 ( 1 10 π ) ( 9 + 6 ) 1 / 3 ( 1 + 3 ) + 2 3 1 / 6 5 1 / 3 ( 9 + 6 ) 1 / 3 ( 1 + 3 ) − 2 3 1 / 6 5 1 / 3 − 1 5 ( 5 + 2 ) 죄악 ( 1 5 π ) ) φ ( 해외의 ( − 6 π ) ) = π − 1 / 2 Γ ( 5 24 ) Γ ( 5 12 ) − 1 / 2 2 − 13 / 24 3 − 1 / 8 죄악 ( 5 12 π ) φ ( 해외의 ( − 1 2 6 π ) ) = π − 1 / 2 Γ ( 5 24 ) Γ ( 5 12 ) − 1 / 2 2 5 / 24 3 − 1 / 8 죄악 ( 5 24 π ) 표시({style{array}{lll}\varphi \left(\expx{\sqrt {2}},\pi)\right)&=&\pi ^{-1/2}\Gamma \left\tfrac {9}{8}\right){\Gamma \left\tfrac {5}}^{8}\varfraft}}^{1/2}\varfright}{\varfraft(\right}{\right}}{\fr,\pi)\right)&=&\pi ^{-1/2}\Gamma \left\tfrac {9}{8}\right){\Gamma \leftfrac {5}{4}}}^{-1/2}^{1/8}{\Bigl(}+{\sqrtfrt{\sq)} rt {2}-1}{\Bigr)}\\\varphi \left(\exp(-3{\sqrt {2}\,\pi)\right;=&\pi ^{-1/2}\Gamma \left\tfrac {9}{8}\right){\Gamma \left\tfrac{5}}\tfrac{2}{3}{ta \ta\rta\rta\rta\rta\rta\rta\rta\rt,\pi)\right)&=&\pi ^{-1/2}\Gamma \leftpa\tfrac {9}{8}\right){\Gamma \leftpa\tfrac {5}{ 4}}\right)}^{-1/2}2^{-1/8}{\Bigl(}1+{\sqrt[{4}]{2}}{\Bigr)}}{\varphi \left(-5{\sqrt {2}})\,\pi)\right)&=&\pi ^{-1/2}\Gamma \leftpa\tfrac{9}{8}}\right){\Gamma \leftpa\tfrac{5}}}^{-1/2}\&&\cdot{biggl(}{\tfrac{5}}{sqrtpa}{\rtpa}{\rtpa}{\rtpa}{\rtpa}{\rtpa}{\r {2}}~3^{1/6}5^{1/3}}{({9+{\sqrt{6}}}}}{1/3}}-{3^{1/6}}-{1}}}-{\tfrac{5}}}({\sqrt{5}+{\sqrtrt{2}}}){{{\var}}\tfrac{\var}{{\var}\tfrac{{\vrtfrac{{\vrtfrac{{{{{{{{\,\pi)\right)&=&\pi ^{-1/2}\Gamma \lefts\tfrac {5}{24}\right){\Gamma \lefts\tfrac {5}}^{-1/2}\right}^{-13/24}3^{\sqrtfrac {5} {12}}}\\varphi \left(\exp({{\tfrac {1}{2}}}{\sqrt {6}}\right)&=&\pi ^{-1/2}\Gamma \left\tfrac {5}{12}\right)}{\Gamma \tfrac \tfrac {5}{12}}}{\tfrac}{\gamma \tfrac}{1/2}{\tfrac}{\fraft}{\frac}}{\frac}{ 힘 정리 없음 직접 전력 정리 세타 함수의 이름[13]
θ 2 ( q 2 ) = 1 2 2 [ θ 3 ( q ) 2 − θ 4 ( q ) 2 ] {\displaystyle \theta _{2}(q^{2})=tftfrac {1}{2}}{\sqrt {2}[\theta _{3}(q)^{2}-\theta _{4}(q)^{2}}}}}}} θ 3 ( q 2 ) = 1 2 2 [ θ 3 ( q ) 2 + θ 4 ( q ) 2 ] {\displaystyle \theta _{3}(q^{2})=tftfrac {1}{2}}{\sqrt {2}[\theta _{3}(q)^{2}+\theta _{4}(q)^{2}}}}}}}} θ 4 ( q 2 ) = θ 4 ( q ) θ 3 ( q ) {\displaystyle \theta _{4}(q^{2})=svsqrt {{4}(q)\theta _{3}(q)}}} 표시 제곱함수를 내부함수로 하는 세 개의 세타 제로값 함수의 제곱도 야코비 항등식에 따라 피타고라스 3중 의 패턴으로 형성됩니다. 또한 이러한 변환은 유효합니다.
θ 3 ( q 4 ) = 1 2 θ 3 ( q ) + 1 2 θ 4 ( q ) {\displaystyle \theta _{3}(q^{4})=tftfrac {1}{2}}\theta _{3}(q)+{\tfrac {1}{2}}\theta _{4}(q)} 다음 공식을 사용하여 이름의 입방체의 세타 값을 계산할 수 있습니다.
27 θ 3 ( q 3 ) 8 − 18 θ 3 ( q 3 ) 4 θ 3 ( q ) 4 − θ 3 ( q ) 8 = 8 θ 3 ( q 3 ) 2 θ 3 ( q ) 2 [ 2 θ 4 ( q ) 4 − θ 3 ( q ) 4 ] \"표시 스타일 27\,\theta _{3}(q^{3)^{8}-18\,\theta _{3}(q^{3})^{4}-\,\theta _{3}(q)^{8}=8,\theta _{3}(q^{3)^{2}\ta_{4}(q)^{4}\ta(ta){4}(ta_4)^(ta_4)^(ta){ta}(ta_ta_ta_ta_4) 27 θ 4 ( q 3 ) 8 − 18 θ 4 ( q 3 ) 4 θ 4 ( q ) 4 − θ 4 ( q ) 8 = 8 θ 4 ( q 3 ) 2 θ 4 ( q ) 2 [ 2 θ 3 ( q ) 4 − θ 4 ( q ) 4 ] \"표시 스타일 27\,\theta _{4}(q^{3)^{8}-18\,\theta _{4}(q^{3})^{4}-\,\theta _{4}(q)^{8}=8,\theta _{4}(q^{3)^{2}\ta_{4}(q){ta}{4}{ta^{ta}(ta){4}(ta^{4){ta}{ta}(ta}(ta)^{4}(t 그리고 다음 공식을 사용하여 nom의 5제곱 세타 값을 계산할 수 있습니다.
[ θ 3 ( q ) 2 − θ 3 ( q 5 ) 2 ] [ 5 θ 3 ( q 5 ) 2 − θ 3 ( q ) 2 ] 5 = 256 θ 3 ( q 5 ) 2 θ 3 ( q ) 2 θ 4 ( q ) 4 [ θ 3 ( q ) 4 − θ 4 ( q ) 4 ] \"표시 스타일 [\theta _{3}(q^{5)^{2}-\theta _{3}(q^{5)^{2}][5\,\theta _{3}(q)^{2}]^{2}-\theta _{3}(q^{5)^{2}^{2},\theta _{3}(q^{ta){4}\ta^{4}\ta} [ θ 4 ( q 5 ) 2 − θ 4 ( q ) 2 ] [ 5 θ 4 ( q 5 ) 2 − θ 4 ( q ) 2 ] 5 = 256 θ 4 ( q 5 ) 2 θ 4 ( q ) 2 θ 3 ( q ) 4 [ θ 3 ( q ) 4 − θ 4 ( q ) 4 ] \"표시 스타일 [\theta _{4}(q^{5)^{2}-\theta _{4}(q^{5)^{2}][5\,\theta _{4}(q)^{2}]^{2}-\theta _{4}(q^{5})^{2}^{2},\theta _{4}(q^{ta})_4}{ta_4}{ta^{ta^{3}\ta}\ta}\ta(ta_ta_4} 이름의 입방근에서의 변환 타원형 명사의 입방근에서 세타 Nullwert 함수 값에 대한 공식은 해당 4차 방정식의 두 실제 해를 대조하여 얻습니다.
[ θ 3 ( q 1 / 3 ) 2 θ 3 ( q ) 2 − 3 θ 3 ( q 3 ) 2 θ 3 ( q ) 2 ] 2 = 4 − 4 [ 2 θ 2 ( q ) 2 θ 4 ( q ) 2 θ 3 ( q ) 4 ] 2 / 3 표시({style\biggl [}{\frac{3}(q^{1/3})^{2}}{\theta_{3}(q^{3})^{2}}-{\theta_{3}(q^{3})^{2}}}{\theta_{3}}{\biggr}}}^{2}=4-{ta}{ta}{ta}{ta}{ta}{ta}{ta}{ta}{ta_{ta}{ta}} [ 3 θ 4 ( q 3 ) 2 θ 4 ( q ) 2 − θ 4 ( q 1 / 3 ) 2 θ 4 ( q ) 2 ] 2 = 4 + 4 [ 2 θ 2 ( q ) 2 θ 3 ( q ) 2 θ 4 ( q ) 4 ] 2 / 3 표시({style\biggl [}{\frac {3\},\theta _{4}(q^{3})^{2}}-{\frac {{4}(q^{1/3})^{2}}-{\frac {4}(q)^{2}}}{\biggr}}^{2}=4+{ta}{ta}{ta^{ta}{ta}{ta}{ta}{ta}{ta}{ta}{ta}{ta}{ta} 이름의 다섯 번째 어근에서의 변환 로저스-라마누잔 연속 분수는 야코비 세타 함수의 관점에서 다음 과 같은 방법으로 정의할 수 있습니다.
R ( q ) = 황갈색의 { 1 2 아크탄 [ 1 2 − θ 4 ( q ) 2 2 θ 4 ( q 5 ) 2 ] } 1 / 5 황갈색의 { 1 2 아크코트 [ 1 2 − θ 4 ( q ) 2 2 θ 4 ( q 5 ) 2 ] } 2 / 5 표시 스타일 R(q)=\tan{\biggl \{}{\frac {1}{2}}\arctan{\frac {1}}-{\frac {{4}(q)^{2}}{2}},\theta _{4}(q^5)^{2}}{\biggr}{\biggr \^1/5}{\tan{frac{frac}{frac}{1}{\frac{\frac}{\frac}{\frac}{\frac}{\frac}{ R ( q 2 ) = 황갈색의 { 1 2 아크탄 [ 1 2 − θ 4 ( q ) 2 2 θ 4 ( q 5 ) 2 ] } 2 / 5 요람 { 1 2 아크코트 [ 1 2 − θ 4 ( q ) 2 2 θ 4 ( q 5 ) 2 ] } 1 / 5 표시 스타일 R(q^{2})=\tan{{\frac{1}{2}}\arctanbiggl[}{\frac{1}}-{\frac{{\frac{4}(q^5)^{2}}{2}},\theta_{4}(q^5)^{2}{\biggr}{\gr\cota}{{{\frac{\frac{1}{\frac}{\frac}{\frac}{\frac}{\frac}{\frac}{ R ( q 2 ) = 황갈색의 { 1 2 아크탄 [ θ 3 ( q ) 2 2 θ 3 ( q 5 ) 2 − 1 2 ] } 2 / 5 황갈색의 { 1 2 아크코트 [ θ 3 ( q ) 2 2 θ 3 ( q 5 ) 2 − 1 2 ] } 1 / 5 표시 스타일 R(q^{2})=\tan{\biggl \{\frac {1}{2}}\arctanbiggl [}{\frac {3}(q^{5)^{2}}{2}}-{\frac {1}{\biggr}{\gr \biggr}{{{\gr}}{{\frac}{{\frac}{{\gla}{ta}{\frac}{{\frac}{{\frac}}{\grac}{\frac}{ 교대 로저스-라마누잔 연속 분수 함수 S(q)는 다음과 같은 두 가지 동일성을 갖습니다.
S ( x ) = R ( q 4 ) R ( q 2 ) R ( q ) = 황갈색의 { 1 2 아크탄 [ θ 3 ( q ) 2 2 θ 3 ( q 5 ) 2 − 1 2 ] } 1 / 5 요람 { 1 2 아크코트 [ θ 3 ( q ) 2 2 θ 3 ( q 5 ) 2 − 1 2 ] } 2 / 5 {\displaystyle S(x)=displayfrac {R(q^{4)}{R(q^{2)}}=\tan{\biggl \{\frac{1}}\arctan{biggl [}{\frac{3}(q)^{2}}}{2}}{\frac{1}{{\grac{1}}\gr}\cota{{\gr}\gr}\cota{{{{{\gr}}}}}}\ta}{{{{{{ \theta _{3}(q^{5})^{2}}-{\frac{1}{2}}{\biggr}}{\biggr \}}^{2/5}} 명사의 다섯 번째 근에서 세타 함수 값은 연속 분수 R 및 S와 명사의 다섯 번째 거듭제곱에서 세타 함수 값의 합리적 조합으로 나타낼 수 있습니다. 다음 네 가지 방정식은 0과 1 사이의 모든 값 q에 대해 유효합니다.
θ 3 ( q 1 / 5 ) θ 3 ( q 5 ) − 1 = 1 S ( q ) [ S ( q ) 2 + R ( q 2 ) ] [ 1 + R ( q 2 ) S ( q ) ] 표시({style\frac{3}(q^{1/5})}{\theta_{3}(q^{5})}}-1=nbfrac{1}{S(q)}{\bigl[}S(q)^{2}+R(q^{2})}{\bigl[}}{\bigl[1+R(q^{2})}S(q)}{\bigr}}}} 1 − θ 4 ( q 1 / 5 ) θ 4 ( q 5 ) = 1 R ( q ) [ R ( q 2 ) + R ( q ) 2 ] [ 1 − R ( q 2 ) R ( q ) ] 표시 스타일 1-{\frac_{4}(q^{1/5})}{\theta_{4}(q^{5}})}{\bigl [}R(q^{2})+R(q)^{2}{\bigr}}{\bigl [}-R(q^{2})}{\bigl [1-R(q^{2})}}(q\bigr}}} θ 3 ( q 1 / 5 ) 2 − θ 3 ( q ) 2 = [ θ 3 ( q ) 2 − θ 3 ( q 5 ) 2 ] [ 1 + 1 R ( q 2 ) S ( q ) + R ( q 2 ) S ( q ) + 1 R ( q 2 ) 2 + R ( q 2 ) 2 + 1 S ( q ) − S ( q ) ] \displaystyle \theta _{3}(q^{1/5})^{2}-\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}-\theta _{3}(q^{5})^{2}}{\bigl[1}+{\frac{R(q^2})}}{R^{2}}{R^{2}{2}{R^{R^{R}}}}}{R^(Q}{2}{R θ 4 ( q ) 2 − θ 4 ( q 1 / 5 ) 2 = [ θ 4 ( q 5 ) 2 − θ 4 ( q ) 2 ] [ 1 − 1 R ( q 2 ) R ( q ) − R ( q 2 ) R ( q ) + 1 R ( q 2 ) 2 + R ( q 2 ) 2 − 1 R ( q ) + R ( q ) ] \displaystyle \theta _{4}(q)^{2}-\theta _{4}(q^{1/5})^{2}=\theta _{4}(q^{5})^{2}-\theta _{4}^{\bigr}}{\bigl[1]-{{\frac{1}}{R(q^2})}{R^{2}{2}{R^{R}{R}{R^{R^(Q)}}}{R^{2}{R^{ 계수 의존 정리 타원 계수와 조합하여 다음 공식을 표시할 수 있습니다.
타원형 명사의 제곱 공식은 다음과 같습니다.
θ 4 [ q ( k ) ] = θ 4 [ q ( k ) 2 ] 1 − k 2 8 {\displaystyle \theta _{4}[q(k)]=\theta _{4}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}} θ 4 [ q ( k ) 2 ] = θ 3 [ q ( k ) ] 1 − k 2 8 {\displaystyle \theta _{4}[q(k)^{2}]=\theta _{3}[q(k)]{\sqrt[{8}]{1-k^{2}}}}} θ 3 [ q ( k ) 2 ] = θ 3 [ q ( k ) ] 코스 [ 1 2 호신. ( k ) ] \"표시 스타일 \theta _{3}[q(k)^{2}]=\theta _{3}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]}} 그리고 이것은 이름의 입방체에 대한 효율적인 공식입니다.
θ 4 ⟨ q { 황갈색의 [ 1 2 아크탄 ( t 3 ) ] } 3 ⟩ = θ 4 ⟨ q { 황갈색의 [ 1 2 아크탄 ( t 3 ) ] } ⟩ 3 − 1 / 2 ( 2 t 4 − t 2 + 1 − t 2 + 2 + t 2 + 1 ) 1 / 2 표시 스타일 \theta _{4}{\biggl \bigle }q{\bigl \{}\tfrac {1}{2}}\arctan(t^{3}){\bigr}}{\bigr \}^{3}{\bigr \gr \rangle }=\theta_{4}{\bigl{\fr}\bigl{\fr}\bigl{\bigr}\bigl{\bigr}\bigr}\bigr}\bigr}\b {\bigr}^{1/2}} 모든 실수 값 t ∈ R displaystyle t\in mathbb }
그리고 이 공식에 대해 두 가지 예를 제시해야 합니다.
값 = 1 displaystyle 1
θ 4 ⟨ q { 황갈색의 [ 1 2 아크탄 ( 1 ) ] } 3 ⟩ = θ 4 ⟨ q { 황갈색의 [ 1 2 아크탄 ( 1 ) ] } ⟩ 3 − 1 / 2 ( 3 + 2 ) 1 / 2 표시 스타일 \theta _{4}{\biggl \bigle}q{bigl \{}\tfrac{1}}\arctan(1){\bigr}}{\bigr \}^{3}{\biggr \rangle }=\theta_{4}{\bigl[{\frac{1}\bigr}\gr}\bigr{r}\bigr}\bigr{1}\bigr(\bigr}\bigr}\bigr}\bigr}
θ 4 [ 해외의 ( − 3 2 π ) ] = θ 4 [ 해외의 ( − 2 π ) ] 3 − 1 / 2 ( 3 + 2 ) 1 / 2 표시 스타일 \theta _{4}{\bigl [}\exp(-3"sqrt {2}}\,\pi){\bigr}}=\theta_{4}{\bigl [}\exp(-{\sqrt {2}}\,\pi){\bigr}}\,3^{-1/2}{\bigl(}}\bigl({\bigrt}}}\bigl({1})^2}^2}}^2}}}^2}{{\big
t = Δ 2 ({ displaystyle Phi 2}}
θ 4 ⟨ q { 황갈색의 [ 1 2 아크탄 ( Φ − 6 ) ] } 3 ⟩ = θ 4 ⟨ q { 황갈색의 [ 1 2 아크탄 ( Φ − 6 ) ] } ⟩ 3 − 1 / 2 ( 2 Φ − 8 − Φ − 4 + 1 − Φ − 4 + 2 + Φ − 4 + 1 ) 1 / 2 표시 스타일 \theta _{4}{\biggl \taule}q{bigl \{}\tanbigl [}{\tfrac{1}{2}}\arctan(\Phi ^{-6}){\bigr \}^{3}{\biggr \rangle}=\thata_{\bigl{\bigl}\bigl{\bigl{\fr}{\bigl{\frac{\fr}{\bigl}{\fr}{\bigl}{\ {{-4}+1}},{\bigr}^{1/2}}
θ 4 [ 해외의 ( − 3 10 π ) ] = θ 4 [ 해외의 ( − 10 π ) ] 3 − 1 / 2 ( 2 Φ − 8 − Φ − 4 + 1 − Φ − 4 + 2 + Φ − 4 + 1 ) 1 / 2 표시 스타일 \theta _{4}{\bigl [}\exp(-3{\sqrt {10}}\,\pi){\bigr}}=\theta _{4}{\bigl [}\exp(-{\sqrt {10}},\pi}{\bigl (}\sqrt {\pi ^2}{8}\i^{4}{i+1}{i}{i}}{i}{i}{i}{i}}{i}}}}{i}{i+1}{
상수 displaystyle \Phi} 골든 비 수 Δ = 12 5 + 1 ) 디스플레이 Phi ltftfrac {1}{2}}({\sqrt {5}}+1)
일부 영상 시리즈 ID 결과에서 세타 함수와 합합니다. 홀수 지수를 갖는 피보나치 수들의 무한[14] [15]
∑ n = 1 ∞ 1 F 2 n − 1 = 5 2 ∑ n = 1 ∞ 2 ( Φ − 2 ) n − 1 / 2 1 + ( Φ − 2 ) 2 n − 1 = 5 4 ∑ a = − ∞ ∞ 2 ( Φ − 2 ) a − 1 / 2 1 + ( Φ − 2 ) 2 a − 1 = 표시 스타일 \sum _{n=1}^{\infty}{\frac {1}{F_{2n-1}}=skfrac {{sqrt {5}}{2}},\sum _{n=1}^{\infty}{\frac {2(\Phi ^{-2})^{1}{1}{1}{1}{{(\Phi ^{n-2}}}{\sqfrac}}{\infty}}}}{frac}{\infty}{\frac}{ = 5 4 θ 2 ( Φ − 2 ) 2 = 5 8 [ θ 3 ( Φ − 1 ) 2 − θ 4 ( Φ − 1 ) 2 ] {\displaystyle = ({sqrt {5}}}{4}},\theta _{2}(\Phi ^{2})^{2}}= (\bigl [})\theta _{3}(\Phi ^{-1})^{2}-\theta _{4}(\Phi ^{-1})^{2}\bigl}}}} 세타 함수 표현식을 사용하지 않음으로써 두 합 사이의 다음 항등식을 공식화할 수 있습니다.
∑ n = 1 ∞ 1 F 2 n − 1 = 5 4 [ ∑ n = 1 ∞ 2 Φ − ( 2 n − 1 ) 2 / 2 ] 2 표시 스타일 \sum _{n=1}^{\infty}{\frac {1}{F_{2n-1}}=sqfrac {{sqrt {5}}{4}},{\biggl [}\sum _{n=1}^{\infty}2\,\Phi ^{-(2n-1)^{2}{\biggr}}^{2}}^{2}}}}^{2}}}{2}}}}}}. ∑ n = 1 ∞ 1 F 2 n − 1 = 1.82451515740692456814215840626732817332 … {\displaystyle \sum _{n=1}^{\infty}{\frac {1}{F_{2n-1}}=1.82451574069245681421584062673217332\ldots} 또한 이 경우 Δ = 12 5 1 ) displaystyle Phi tftfrac {1}{2}}({\sqrt {5}}+1)} 골든 비율 숫자입니다.
피보나치 수 제곱의 무한 합:
∑ n = 1 ∞ 1 F n 2 = 5 24 [ 2 θ 2 ( Φ − 2 ) 4 − θ 3 ( Φ − 2 ) 4 + 1 ] = 5 24 [ θ 3 ( Φ − 2 ) 4 − 2 θ 4 ( Φ − 2 ) 4 + 1 ] \displaystyle \sum _{n=1}^{\infty}{\frac {1}{F_{n}^{2}}=nbigl {5}{24}}{\bigl [}2},\theta _{2}(\Phi ^{-2})^{4}-\tha _{3}^{4}^{4}^{2}{\frac{\ta}{2}{\ta}{\ta}{\ta}\ta}\ta. 홀수 지수를 갖는 Pell 숫자의 역수 무한 합:
∑ n = 1 ∞ 1 P 2 n − 1 = 1 2 θ 2 [ ( 2 − 1 ) 2 ] 2 = 1 2 2 [ θ 3 ( 2 − 1 ) 2 − θ 4 ( 2 − 1 ) 2 ] \displaystyle \sum _{n=1}^{\infty}{\frac {1}{P_{2n-1}}={\sqrt {2}}\,\theta_{2}{\bigl [}({\sqrt {2}-1})^{2}}^{2}={\bigrta}{\sqrta}{2}{ta}{\sqrta}{3}{ta}{ta}{\rta}{\rta}{ta summand의 theta 함수와 합 다음 두 개의 시리즈 동일성은 이스반 [16] 메조 에 의해 증명되었습니다.
θ 4 2 ( q ) = i q 1 4 ∑ k = − ∞ ∞ q 2 k 2 − k θ 1 ( 2 k − 1 2 i 인 q , q ) , θ 4 2 ( q ) = ∑ k = − ∞ ∞ q 2 k 2 θ 4 ( k 인 q i , q ) . 표시(\style{aligned}\theta_{4}^{2}(q)&=iq^{\frac{1}}\sum_{k=-\infty}^{2k^{2}-k}\theta_{1}\ta\ta\ta\ta\frac{4}{q,\right},\[6]\ta_{4}{k^{k^{k-}\infty}{k^{k^{k^{k-}\infty}\fty}\ta \end{aligned}}} 이러한 관계는 모든 0 < q < 1 . q 의 값을 특수화하면, 다음 매개 변수 자유 합이 있습니다.
π e π 2 ⋅ 1 Γ 2 ( 3 4 ) = i ∑ k = − ∞ ∞ e π ( k − 2 k 2 ) θ 1 ( i π 2 ( 2 k − 1 ) , e − π ) 표시({\frac {\frac {\pi}}{2}}\cdot {frac {1}{\Gamma ^{2}\left({\frac {3}{4}}\right) }}=i\sum _{k=-\infty}^{\infty }e^{\pi \left(k-2k^{2}\right) }\theta _{1}\left\frac{i\pi}{2}}(2k-1), e^{-\pi}\right)} π 2 ⋅ 1 Γ 2 ( 3 4 ) = ∑ k = − ∞ ∞ θ 4 ( i k π , e − π ) e 2 π k 2 표시({\frac {3}{4}}\right) }}=\sum _{k=-\infty}^{\infty}{\frac{theta_{4}\left(ik\pi,e^{-\pi}\right) }{e^{2\pi k^{2}}}}} 야코비테타 함수의 0 Jacobi theta 함수의 모든 0은 단순 0이며 다음과 같이 제공됩니다.
ϑ ( z ; τ ) = ϑ 00 ( z ; τ ) = 0 ⟺ z = m + n τ + 1 2 + τ 2 ϑ 11 ( z ; τ ) = 0 ⟺ z = m + n τ ϑ 10 ( z ; τ ) = 0 ⟺ z = m + n τ + 1 2 ϑ 01 ( z ; τ ) = 0 ⟺ z = m + n τ + τ 2 표시({style{aligned}\vartheta(z;\vartheta)=\vartheta_{00}(z;\vartheta)&=0\vartheta&\LongLeft오른쪽 화살표 &&\lambda z&=m+n\lambda +{\frac {1}{2}}+{\frac {{2}}\[3pt]\vartheta _{11}(z;\lambda)&=0\lambda&\Long left 오른쪽 화살표 &&\lambda z&=m+n\lambda \\[3pt]\vartheta _{10}(z;\lambda)&=0\lambda &\Longleft 오른쪽 화살표 &&\beta z&=m+n\beta +{\frac {1}{2}}\[3pt]\vartetha _{01}(z;\filename)&=0\filename &\Longleft 오른쪽 화살표 &&\filename z&=m+n\frac +{\frac {{2}}\end{aligned}}} 여기 서 m, n 은 임의의 정수입니다.
리만 제타 함수와의 관계 관계
ϑ ( 0 ; − 1 τ ) = ( − i τ ) 1 2 ϑ ( 0 ; τ ) {\displaystyle \vartheta \left(0;-{\frac {1}{\frac }}\right)=\leftpxi\frac \light)^{\frac {1}{2}}\vartheta(0;\displaystyle)} 리만 은 멜린 변환을 통해 리만 제타 함수에 대한 함수 방정식을 증명하기 위해 사용되었습니다.
Γ ( s 2 ) π − s 2 ζ ( s ) = 1 2 ∫ 0 ∞ ( ϑ ( 0 ; i t ) − 1 ) t s 2 d t t {\displaystyle \Gamma \left\frac {s}{2}}\right)\pi ^{-{\frac {s}{2}}\zeta(s)={1}{2}}\int_{0}^{\infty}{\vartheta(0;it)-1}}{\frac{{math}}t}}t s 를 1 - s z ≠ 0 에 해당 하는 적분은 후르비츠 제타 함수에 대한 기사에 나와 있습니다.
바이어슈트라스 타원함수와의 관계 세타 함수는 위의 네 개의 세타 함수의 계수로서 그의 타원 함수를 구성하기 위해 (쉽게 계산할 수 있는 형태로) 야코비에 의해 사용되었고, 그는 또한 바이어슈트라스의 타원 함수를 구성하기 위해 사용될 수 있었습니다.
℘ ( z ; τ ) = − ( 로그. ϑ 11 ( z ; τ ) ) ″ + c {\displaystyle \wp (z;\big)=-{\big (}\log \vartetha _{11}(z;\big)}'+c} 여기서 두 번째 도함수는 z에 대한 것 이고 상수 c는 z = 0 에서 π ( z)의 로랑 확장 이 0 상수 항을 갖도록 정의됩니다.
q-감마 함수와의 관계 네 번째 세타 함수(다른 함수도 마찬가지)는 관계를 통해[17] 잭슨 q-감마 함수와 밀접하게 연결됩니다.
( Γ q 2 ( x ) Γ q 2 ( 1 − x ) ) − 1 = q 2 x ( 1 − x ) ( q − 2 ; q − 2 ) ∞ 3 ( q 2 − 1 ) θ 4 ( 1 2 i ( 1 − 2 x ) 로그. q , 1 q ) . \displaystyle \left(\Gamma _{q^{2}}(x)\Gamma _{q^{2}}(1-x)\right)^{-1}=sysfrac {q^{2x(1-x)}}{\left(q^{-2};q^{-2}\right)_{\inft(q^{2}-1}\right)}\right) }}\theta _{4}\left\frac{1}{2i}}(1-2x)\log q,{\frac{1}{q}}\right)}. 데데킨데타 함수와의 관계 η (τ 데데킨데타 함수로 하고, 세타의 인수를 nom q e πiτ 그리고나서,
θ 2 ( q ) = ϑ 10 ( 0 ; τ ) = 2 η 2 ( 2 τ ) η ( τ ) , θ 3 ( q ) = ϑ 00 ( 0 ; τ ) = η 5 ( τ ) η 2 ( 1 2 τ ) η 2 ( 2 τ ) = η 2 ( 1 2 ( τ + 1 ) ) η ( τ + 1 ) , θ 4 ( q ) = ϑ 01 ( 0 ; τ ) = η 2 ( 1 2 τ ) η ( τ ) , 표시({style{aligned})\theta_{2}(q)=\vartheta_{10}(0;\deta)&=deta{2\ta^{2}(2\deta)},\[3pt]\ta_{3}(q)=\vartheta_{00}(0;\deta)&\ta{ta}{ta}{ta}{ta}{\ta}\deta}{\ta}{\ta}{\ta}{\ }{\eta(\ta +1)},\\[3pt]\theta_{4}(q)=\vartheta_{01}(0;\tau)&=taufrac{{eta^{2}\tau\frac{2}}\tau \right) }{\eta (\deta)},\end{aligned}}} 그리고.
θ 2 ( q ) θ 3 ( q ) θ 4 ( q ) = 2 η 3 ( τ ) . \displaystyle \theta _{2}(q)\,\theta _{3}(q)\,\theta _{4}(q)=2\eta ^{3}(\deta)}을(를) 표시합니다. Weber 모듈식 함수도 참조하십시오.
타원 계수 타원 계수 는 다음과 같습니다.
k ( τ ) = ϑ 10 ( 0 ; τ ) 2 ϑ 00 ( 0 ; τ ) 2 {\displaystyle k(\displaystyle)=displayfrac{vartheta_{10}(0;\displaystyle)^{2}}{\vartheta_{00}(0;\displaystyle)^{2}}}} 그리고 상보적인 타원 계수는
k ′ ( τ ) = ϑ 01 ( 0 ; τ ) 2 ϑ 00 ( 0 ; τ ) 2 {\displaystyle k'(\displaystyle k')=displayfrac{vartheta_{01}(0;\displaystyle)^{2}}{\vartheta_{00}(0;\displaystyle)^{2}}}} 세타 함수의 도함수 두 번째 종류의 완전한 타원 적분에 대한 두 가지 동일한 정의는 다음과 같습니다.
E ( k ) = ∫ 0 π / 2 1 − k 2 죄악 ( φ ) 2 ∂ φ {\displaystyle E(k)=\int _{0}^{\pi /2}{\sqrt {1-k^{2}\sin(\varphi)^{2}}\displaystyle \varphi} E ( k ) = π 2 ∑ a = 0 ∞ [ ( 2 a ) ! ] 2 ( 1 − 2 a ) 16 a ( a ! ) 4 k 2 a {\displaystyle E(k)=displayfrac{pi}{2}}\sum _{a=0}^{\infty}{\frac{(2a)!] ^{2}}{{(1-2a)16^{a}(a!) ^{4}}k^{2a}} Theta Nullwert 함수의 파생 모델에는 다음과 같은 MacLaurin 시리즈가 있습니다.
θ 2 ′ ( x ) = d d x θ 2 ( x ) = 1 2 x − 3 / 4 + ∑ n = 1 ∞ 1 2 ( 2 n + 1 ) 2 x ( 2 n − 1 ) ( 2 n + 3 ) / 4 \"표시 스타일 \theta _{2}'(x)={\mathrm {d}{\mathrm {d}x}\,\theta _{2}(x)={n1}{2}x^{2}\sum _{n=1}^{\infty}{\frac{1}{2}(2n+1)^{2}x(2+3)}/4}}}{\}}}}} θ 3 ′ ( x ) = d d x θ 3 ( x ) = 2 + ∑ n = 1 ∞ 2 ( n + 1 ) 2 x n ( n + 2 ) {\displaystyle \theta _{3}'(x)=displayfrac{mathrm {d}{\mathrm {d} x}}\,\theta _{3}(x)=2+\sum _{n=1}^{\infty}2(n+1)^{2} }x^{n(n+2)}}} θ 4 ′ ( x ) = d d x θ 4 ( x ) = − 2 + ∑ n = 1 ∞ 2 ( n + 1 ) 2 ( − 1 ) n + 1 x n ( n + 2 ) {\displaystyle \theta _{4}'(x)=displayfrac{\mathrm {d}{\mathrm {d} x}}\,\theta _{4}(x)=-2+\sum _{n=1}^{\infty}2(n+1)^{n+1}x(n+2)}}}}}}} 제로 값 함수의[18]
θ 2 ′ ( x ) = d d x θ 2 ( x ) = 1 2 π x θ 2 ( x ) θ 3 ( x ) 2 E [ θ 2 ( x ) 2 θ 3 ( x ) 2 ] \"표시 스타일 \theta _{2}'(x)={\mathrm {d}{\mathrm {d}x}}\,\theta _{2}(x)={2\pix}\theta _{3}(x)^{2}E{\frac{\ta}{\ta}{\ta}{\gr}}}{ta}{ta}}{gr}}{ta}}}{gr}}{gr. θ 3 ′ ( x ) = d d x θ 3 ( x ) = θ 3 ( x ) [ θ 3 ( x ) 2 + θ 4 ( x ) 2 ] { 1 2 π x E [ θ 3 ( x ) 2 − θ 4 ( x ) 2 θ 3 ( x ) 2 + θ 4 ( x ) 2 ] − θ 4 ( x ) 2 4 x } \"표시 스타일 \theta _{3}'(x)={\mathrm {d}{\mathrm {d}x}}\,\theta _{3}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr}{\frac{ta}{ta}{\bigl}{ta}{ta}{ta\bigl}{ta}{ta}{ta}{ta}{ta θ 4 ′ ( x ) = d d x θ 4 ( x ) = θ 4 ( x ) [ θ 3 ( x ) 2 + θ 4 ( x ) 2 ] { 1 2 π x E [ θ 3 ( x ) 2 − θ 4 ( x ) 2 θ 3 ( x ) 2 + θ 4 ( x ) 2 ] − θ 3 ( x ) 2 4 x } \"표시 스타일 \theta _{4}'(x)={\mathrm {d}{\mathrm {d}x}}\,\theta _{4}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}^{\bigr}{\gl \frac{1}{ta\bigl}{ta}{ta}{ta\bigl}{ta}{ta}{ta}{ta}{ta}{ta\big 마지막으로 언급된 두 공식은 실수 . x 1 x ∩ ∈ R displaystyle x 1 cap x in mathbb {R }
그리고 마지막으로 명명된 두 개의 세타 미분 함수는 다음과 같은 방식으로 서로 관련이 있습니다.
ϑ 4 ( x ) [ d d x ϑ 3 ( x ) ] − ϑ 3 ( x ) [ d d x θ 4 ( x ) ] = 1 4 x θ 3 ( x ) θ 4 ( x ) [ θ 3 ( x ) 4 − θ 4 ( x ) 4 ] 표시 스타일 \vartheta _{4}(x){\biggl [}{\frac{mathrm{d}x}}\,\vartheta_{3}(x){\biggr}}-\vartheta_{3}(x){\biggl [}{\frac{\mathrm{d}}}}{\ta{x},\ta},\ta{4(\gr},\ta},\ta},\ta}{ta{\ta}{ta}{ 여기서 언급된 세타 함수 중 두 개의 계수의 도함수는 항상 이 세 함수와 합리적인 관계를 갖습니다.
d d x θ 2 ( x ) θ 3 ( x ) = θ 2 ( x ) θ 4 ( x ) 4 4 x θ 3 ( x ) style {\frac {\mathrm {d}{\mathrm {d}x}\,{\frac {{2}(x)}{\theta _{3}(x)}={frac {{2}(x)},\theta _{4}^{4}}{4,x\theta {3}}표시 d d x θ 2 ( x ) θ 4 ( x ) = θ 2 ( x ) θ 3 ( x ) 4 4 x θ 4 ( x ) style {\frac {\mathrm {d}{\mathrm {d}x}\,{\frac {{2}(x)}{\theta _{4}(x)}={frac {{2}(x)},\theta _{3}^{4}}{4,x\theta {4}}표시 d d x θ 3 ( x ) θ 4 ( x ) = θ 3 ( x ) 5 − θ 3 ( x ) θ 4 ( x ) 4 4 x θ 4 ( x ) 표시(\style\frac{\mathrm{d}{\mathrm{d}x})\,{\frac{theta_{3}(x)}={frac{3}^{5}-\theta_{3}(x)\theta_{4}^{4}}}{4,x,\theta_{4}}{4},\theta_ta{4}(x}}}}를 표시합니다. 이러한 파생 공식의 파생은 Nome(수학) 및 Modular 람다 함수를 참조하십시오!
세타 함수의 적분 세타 함수의 경우 다음 적분이[19]
∫ 0 1 θ 2 ( x ) d x = ∑ k = − ∞ ∞ 4 ( 2 k + 1 ) 2 + 4 = π 황갈색의 ( π ) ≈ 3.129881 {\displaystyle \int _{0}^{1}\theta _{2}(x)\,\mathrm {d} x=\sum _{k=-\infty}^{\infty}{\frac {4}{(2k+1)^{2}+4}=\pi \tanh(\pi)\ta 3.129881} ∫ 0 1 θ 3 ( x ) d x = ∑ k = − ∞ ∞ 1 k 2 + 1 = π 코트 ( π ) ≈ 3.153348 {\displaystyle \int _{0}^{1}\theta _{3}(x)\,\mathrm {d} x=\sum _{k=-\infty}^{\infty}{\frac {1}{k^{2}+1}}=\pi \coth(\pi)\discont 3.153348} ∫ 0 1 θ 4 ( x ) d x = ∑ k = − ∞ ∞ ( − 1 ) k k 2 + 1 = π csch ( π ) ≈ 0.272029 \"표시 스타일 \int _{0}^{1}\theta _{4}(x)\,\mathrm {d} x=\sum _{k=-\infty}^{\infty}{\frac {(-1)^{k}}{k^{2}+1}}}=\pi \,\operatorname {csch}(\pi)\deta0.272029} 이제 표시된 최종 결과는 일반적인 코시 합계 공식을 기반으로 합니다.
열방정식의 해 야코비 세타 함수는 공간적으로 주기적인 경계 [20] 1차원 열 방정식 의 기본 솔루션입니다. z x τ 그것 을 현실과 긍정으로 가정하면, 우리는 쓸 수 있습니다.
ϑ ( x ; i t ) = 1 + 2 ∑ n = 1 ∞ 해외의 ( − π n 2 t ) 코스 ( 2 π n x ) {\displaystyle \vartheta (x;it)=1+2\sum _{n=1}^{\infty}\exp \lefts\pin^{2}t\right)\cos(2\pinx)} 열 방정식을 푸는 것은
∂ ∂ t ϑ ( x ; i t ) = 1 4 π ∂ 2 ∂ x 2 ϑ ( x ; i t ) . 표시({style\frac \\fartheta (x;it)=vardfrac {1}{4\pi }{\frac {\frac \fartheta ^{2}}{\frac x^{2}}\vartheta (x;it)} 이 세타 함수 솔루션은 x 에서 1차원 함수이며, t → 0 으로서 분포 의 의미에서 주기적 델타 함수 또는 Diraccomb 에 접근합니다.
한계 → 0 ϑ x it = ∞ n = δ x displaystyle \lim {t\to }\vartheta (x;it sum {n infty}^{\infty}\ (x-n 열 방정식에 대한 공간 주기적 초기값 문제의 일반적인 해결책은 t = 0 에서 초기
하이젠베르크 군과의 관계 자코비 세타 함수는 하이젠베르크 그룹의 이산 부분군의 작용 하에서 불변합니다. 이 불변성은 하이젠베르크 그룹의 세타 표현 에 관한 기사에 제시되어 있습니다.
일반화 만약 F가 n개 변수 의 2차 형태라면, F 와 연관된 세타 함수는
θ F ( z ) = ∑ m ∈ Z n e 2 π i z F ( m ) {\displaystyle \theta _{F}(z)=\sum _{m\in \mathbb {Z}^{n}}e^{2\piizF(m)}}} 정수 Zn ({ displaystyle \mathbb {Z}^{n 이 세타 함수는 모듈식 그룹의 (적절하게 정의된 부분군에 대한) 가중치 / 2 모듈식 형식입니다. 푸리에 확장에서,
θ ^ F ( z ) = ∑ k = 0 ∞ R F ( k ) e 2 π i k z , 표시({style\hat\theta}_{F}(z)=\sum_{k=0}^{\infty}R_{F}(k)e^{2\piikz}} 숫자F R (표현 번호라고 불립니다.
디리클레 캐릭터의 세타 시리즈 χ 원시 디리클레 문자 모듈로 q 및 ν χ 2
θ χ ( z ) = 1 2 ∑ n = − ∞ ∞ χ ( n ) n ν e 2 i π n 2 z \displaystyle \theta _{\chi }(z)=displayfrac {1}{2}}\sum_{n=-\infty}^{\infty}\chi(n)n^{\nu }e^{2i\pin^{2}z}}} 가중치 / 2 ν 4q2 및 문자 형식입니다.
χ ( d ) ( − 1 d ) ν , {\displaystyle \chi (d)\left\frac {-1}{d}\right)^{\nu }} 즉[21]
θ χ ( a z + b c z + d ) = χ ( d ) ( − 1 d ) ν ( θ 1 ( a z + b c z + d ) θ 1 ( z ) ) 1 + 2 ν θ χ ( z ) {\displaystyle \theta _{\chi }\left\frac {az+b}{cz+d}}\right) =\chi (d)\lefts\frac{-1}{d}\right)^{\nu}\lefts\frac{{1}\lefts\frac{az+b}{cz+d}\right) }{\theta _{1}(z)}}\right)^{1+2\nu }\theta _{\chi }(z)} 언제든지
a , b , c , d ∈ Z 4 , a d − b c = 1 , c ≡ 0 모드 4 q 2 . displaystyle a,b,c,d\in \mathbb {Z}^{4},ad-bc=1,c\equiv 0"bmod {4}}q^{2}}. 라마누잔세타 함수 리만 세타 함수 허락하다
H n = { F ∈ M ( n , C ) F = F T , 임 F > 0 } {\displaystyle \mathbb {H} _{n}=\left\{ F\in M(n,\mathbb {C})\,{\big}\,F=F^{\mathsf{T}}\,,\,\operator 이름 {Im} F>0\right\} 가상 부분이 양 의 확실한 대칭 제곱 행렬의 집합 입니다. Hn { displaystyle \mathbb {H}_{n}} 시겔 상부 반공간 이라고 하며 상부 반평면 의 다차원 아날로그입니다.모듈러 군의 n차원 유사체는 심플렉틱 군 Sp(2n, Z{ displaystyle \mathbb {Z }) 1 에 대해 (2, {displaystyle \mathbb {Z SL(2, Z{ displaystyle \mathbb {Z })합동 부분군의 n차원 아날로그는 다음과 같이 재생됩니다.
케르 { Sp ( 2 n , Z ) → Sp ( 2 n , Z / k Z ) } . \displaystyle \ker \big \{}\operatorname {Sp}(2n,\mathbb {Z})\to \operatorname {Sp}(2n,\mathbb {Z} /k\mathbb {Z}({\big \}){\big \}}. 그리고, τ Hn {{ displaystyle \mathbb {H}_{n 리만 세타 함수는 다음과 같이 정의됩니다.
θ ( z , τ ) = ∑ m ∈ Z n 해외의 ( 2 π i ( 1 2 m T τ m + m T z ) ) . \"displaystyle \theta (z,\mathbb)=\sum _{m\in \mathbb {Z}^{n}}\exp \left(2\pii\left\tfrac {1}{2}}m^{\mathsf{T}}\taum+m^{\mathsf{T}z\right)\right}. 여기 Cn { displaystyle \mathbb {C}^{n}} 초첨자 T는 전치 를 나타냅니다.자코비 세타 함수는 n = 1 및 displaystyle \mathbb {H} 특수 여기 displaystyle \mathbb {H} 상위 반평면입니다. 리만 세타 함수의 주요 응용 중 하나는 첫 번째 호몰로지 그룹에 대한 표준 기저에 대한 주기 행렬로 γ 를 취함으로써 콤팩트 리만 표면과 함수 이론에서 두드러지게 나타나는 다른 보조 물체에 대한 명시적인 공식을 제공할 수 있다는 것입니다.
리만 세타는 Cn × Hn displaystyle \mathbb {C}^{n}\times mathbb {H}_{n
함수 방정식은 다음과 같습니다.
θ ( z + a + τ b , τ ) = 해외의 ( 2 π i ( − b T z − 1 2 b T τ b ) ) θ ( z , τ ) \"표시 스타일 \theta(z+a+\tau b,\tau)=\exp \left(2\pii\left\mathsf b^{\mathsf {T}}z-{\tfrac {1}{2}}b^{\mathsf {T}\tau\right)\right)\tha(z,\theta)} 이 값은 모든 벡터 b Zn { displaystyle \mathbb {Z} n 모든 ∈ Cn mathbb {C} n} Hn displaystyle \mathbb {H} _{n
푸앵카레 계열 Poincaré 시리즈는 임의의 Fuchsian 그룹에 대해 세타 시리즈를 오토모픽 형태로 일반화합니다.
세타 함수 계수 만약 a π (n )함수와 q < 1 ,
∑ n = 1 ∞ χ ( n ) q a n 2 + b n = ∑ n = 1 ∞ q n ∑ a d 2 + b d = n d n χ ( d ) . \displaystyle \sum _{n=1}^{\infty }\chi (n)q^{an^{2}+bn}=\sum _{n=1}^{\infty }q^{n}\sum _{\stackrel {d n}{ad^{2}+bd=n}\chi (d) f(n ) 와 π(n )가 임의의 산술 함수이고, f n ) displaystyle \mathbb {N} → displaystyle \mathbb {N } (0) = 0과 함께 엄밀하게 증가 하는 일반적인 경우는 다음과 같습니다.
∑ n = 1 ∞ χ ( n ) q f ( n ) = ∑ n = 1 ∞ q n ∑ d n ∑ f ( δ ) d χ ( δ ) μ의 ( d f ( δ ) ) . \displaystyle \sum _{n=1}^{\infty }\chi (n)q^{f(n)}=\sum _{n}^{\infty }q^{n}\sum _{f(\infty)d}\chi (\chem)\mu \left\frac {d}{f(\infty)}\right}. 세타 값 도출 오일러 베타 함수의 항등식 다음에서 세 가지 중요한 세타 함수 값을 예로 들 수 있습니다.
오일러 베타 함수는 다음과 같이 축소된 형태로 정의됩니다.
β ( x ) = Γ ( x ) 2 Γ ( 2 x ) {\displaystyle \displaystyle (x)=displayfrac{Gamma (x)^{2}}{\Gamma (2x)}}} 일반적으로 모든 자연수 ∈ N displaystyle in \mathbb }
4 − 1 / ( n + 2 ) n + 2 csc ( π n + 2 ) β [ n 2 ( n + 2 ) ] = ∫ 0 ∞ 1 x n + 2 + 1 d x 표시({style\frac{4^{-1/(n+2)}{n+2}}\csc{bigl(}{\fracpi}{n+2}}}{\bigr}}{\biggr}}=\int_{0}^{\infty}{\sqrt{x^{n+2}}}{\math}}{d} 예시적인 타원 적분 다음에서 일부 타원 적분 특이치 가[22]
통합 ID와 이름의 조합 타원 함수에는 다음과 같은 중요한 값이 있습니다.
q ( 1 2 2 ) = 해외의 ( − π ) {\displaystyle q({\tfrac {1}{2}}{\sqrt {2}}=\exp(-\pi )} q [ 1 4 ( 6 − 2 ) ] = 해외의 ( − 3 π ) {\displaystyle q[{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})]=\exp(-{\sqrt {3}}\,\pi )} q ( 2 − 1 ) = 해외의 ( − 2 π ) {\displaystyle q({\sqrt {2}}-1)=\exp(-{\sqrt {2}},\pi )} 이러한 명명 값의 정확성에 대한 증거는 명명(수학) 문서를 참조하십시오!
위에서 언급한 정의 및 본 문서의 동일한 섹션에 있는 세타 함수에 대한 이러한 적분 동일성에 기초하여 모범적인 세타 제로 값이 지금 결정되어야 합니다.
θ 3 [ q ( k ) ] = 2 π − 1 K ( k ) {\displaystyle \theta _{3}[q(k)]=sksqrt {2\pi ^{-1}K(k)}}}
θ 3 [ 해외의 ( − π ) ] = θ 3 [ q ( 1 2 2 ) ] = 2 π − 1 K ( 1 2 2 ) = 2 − 1 / 2 π − 1 / 2 β ( 1 4 ) 1 / 2 = 2 − 1 / 4 π 4 Γ ( 3 4 ) − 1 \displaystyle \theta _{3}[\exp(-\pi )]=\theta _{3}[q({\tfrac {1}{2}}{\sqrt {2}}]={sqrt {2}}K({\tfrac {1}}}{\sqrt{2}}}}=2^{1-1}{\frac{4}{4}}{\sqrtpi}}}{1}}{\rtpi}}}}}}}}{\tfrac{\ θ 3 [ 해외의 ( − 3 π ) ] = θ 3 { q [ 1 4 ( 6 − 2 ) ] } = 2 π − 1 K [ 1 4 ( 6 − 2 ) ] = 2 − 1 / 6 3 − 1 / 8 π − 1 / 2 β ( 1 3 ) 1 / 2 \displaystyle \theta _{3}[\exp(-{\sqrt {3}\,\pi )]=\theta _{3}{\bigl \{{}qrt {4}}({\sqrt {6}}-{\sqrt {2}}){\bigr}}{\bigr}}}=sqrtrtrtrtrt{2\pi^{\bigrt{\bigrt{{\big}{\rt}{2}{\rt θ 3 [ 해외의 ( − 2 π ) ] = θ 3 [ q ( 2 − 1 ) ] = 2 π − 1 K ( 2 − 1 ) = 2 − 1 / 8 코스 ( 1 8 π ) π − 1 / 2 β ( 3 8 ) 1 / 2 \displaystyle \theta _{3}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{3}[q({\sqrt {2}-1}]={2\pi ^{-1}K({\sqrt{2}}-1})=2^{-1/8}\cospi}\tfrac{1}\pi^{1}{1/2}{1/2}{\frac}{\t}{\t}}}}{t}{ θ 4 [ q ( k ) ] = 1 − k 2 4 2 π − 1 K ( k ) {\displaystyle \theta _{4}[q(k)]=nbsqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi^{-1}K(k))}}
θ 4 [ 해외의 ( − 2 π ) ] = θ 4 [ q ( 2 − 1 ) ] = 2 2 − 2 4 2 π − 1 K ( 2 − 1 ) = 2 − 1 / 4 코스 ( 1 8 π ) 1 / 2 π − 1 / 2 β ( 3 8 ) 1 / 2 \displaystyle \theta _{4}[\exp(-{\sqrt {2}\,\pi )]=\theta _{4}[q({\sqrt {2}-1}]={2}\sqrt {2}-2},{\sqrt {2}\pi^{\sqrt}K({\sqrt}-1})}=2^{1}\cos{1}{1}\t}\t}\ta{\t}\t}\t}\t}\ 파티션 시퀀스 및 Pochhammer 제품 정규 파티션 번호 순서 정규 파티션 시퀀스 ( n ) displaystyle (n)} 양의 정수 n = 1 displaystyle 1 5 displaystyle 5 경우 번호 displaystyle }
P(n) 및 관련 숫자 파티션의 예제 값 n P(n) 지불 칸막이 0 1 () 빈 파티션/빈 합계 1 1 (1) 2 2 (1+1), (2) 3 3 (1+1+1), (1+2), (3) 4 5 (1+1+1+1), (1+1+2), (2+2), (1+3), (4) 5 7 (1+1+1+1+1), (1+1+1+2), (1+2+2), (1+1+3), (2+3), (1+4) , (5)
일반 파티션 번호 시퀀스의 생성 함수는 다음과 같은 방법으로 Pochhammer 제품을 통해 나타낼 수 있습니다.
∑ k = 0 ∞ P ( k ) x k = 1 ( x ; x ) ∞ = θ 3 ( x ) − 1 / 6 θ 4 ( x ) − 2 / 3 [ θ 3 ( x ) 4 − θ 4 ( x ) 4 16 x ] − 1 / 24 {\displaystyle \sum _{k=0}^{\infty}P(k)x^{k}=\theta_{3}(x)^{-1/6}}=\theta_{3}^{-2/3}{\big[x]}{\fractheta{3}^{4(x)\ta}{4}{x}{gr}{x}{x}{gr}{x}{x}{gr}}}{4}{4}}}}}}}{gr}}}{ 이제 언급된 포치해머 곱의 요약은 오각수 정리에 의해 다음과 같이 설명됩니다.
( x ; x ) ∞ = 1 + ∑ n = 1 ∞ [ − x Fn ( 2 n − 1 ) − x 크르 ( 2 n − 1 ) + x Fn ( 2 n ) + x 크르 ( 2 n ) ] \"displaystyle (x;x)_{\infty}=1+\sum _{n=1}^{\infty}{\bigl [}-x^{\text{Fn}(2n-1)}}-x^{\text{Fn}}(2n)}+x^{\text{\text{Kr}}}\bigl} 다음의 기본 정의는 오각형 번호와 카드 하우스 번호에 적용됩니다.
Fn ( z ) = 1 2 z ( 3 z − 1 ) 표시{style{text{Fn}}(z)=tftfrac {1}{2}}z(3z-1)} 크르 ( z ) = 1 2 z ( 3 z + 1 ) 표시{style{text{Kr}(z)=tftfrac{1}{2}}z(3z+1)} 추가적으로[23]
( x ; x ) 3 = ∏ n = 1 ∞ ( 1 − x n ) 3 = ∑ m = 0 ∞ ( − 1 ) m ( 2 m + 1 ) x m ( m + 1 ) / 2 {\displaystyle (x;x)^{3}=\displaystyle _{n=1}^{\infty}(1-x^{n})^{3}=\sum _{m=0}^{\infty}(-1)^{m}(2m+1)x^{m(m+1)/2}}}} 엄격한 파티션 번호 순서 그리고 엄밀한 분할 순서 n displaystyle (n [24] 파티션에 홀수 합계만 포함된 경우에도 정확히[25] 다음 표에서는 엄격한 파티션 번호 시퀀스에 대한 두 가지 표현을 비교합니다.
Q(n) 및 관련 숫자 파티션의 예제 값 n Q(n) 반복 합계가 없는 파티션 수 홀수 추가만 있는 파티션 수 0 1 () 빈 파티션/빈 합계 () 빈 파티션/빈 합계 1 1 (1) (1) 2 1 (2) (1+1) 3 2 (1+2), (3) (1+1+1), (3) 4 2 (1+3), (4) (1+1+1+1), (1+3) 5 3 (2+3), (1+4), (5) (1+1+1+1+1), (1+1+3), (5) 6 4 (1+2+3), (2+4), (1+5), (6) (1+1+1+1+1+1), (1+1+1+3), (3+3), (1+5) 7 5 (1+2+4), (3+4), (2+5), (1+6), (7) (1+1+1+1+1+1+1), (1+1+1+1+3), (1+3+3), (1+1+5), (7) 8 6 (1+3+4), (1+2+5), (3+5), (2+6), (1+7), (8) (1+1+1+1+1+1+1+1), (1+1+1+1+1+3), (1+1+3+3), (1+1+1+ 5), (3+5), (1+7)
엄격한 파티션 번호 시퀀스의 생성 함수는 Pochhammer의 제품을 사용하여 나타낼 수 있습니다.
∑ k = 0 ∞ Q ( k ) x k = 1 ( x ; x 2 ) ∞ = θ 3 ( x ) 1 / 6 θ 4 ( x ) − 1 / 3 [ θ 3 ( x ) 4 − θ 4 ( x ) 4 16 x ] 1 / 24 {\displaystyle \sum _{k=0}^{\infty}Q(k)x^{k}=codiffrac{1}{(x;x^{2})_{\infty }}=\theta_{3}(x)^{1/6}\biggl[}{\frac{{\3(x)}{4}{ta}{gr}{4}{ta}{gr}{4}{4}{gr}{x}}}}{x}}{gr}}}{ta 오버파티션 번호 시퀀스 함수01 매클로린 [26] 과분수열의 수 를 양수 부호를 갖는 계수로 합니다.
1 θ 4 ( x ) = ∏ n = 1 ∞ 1 + x n 1 − x n = ∑ k = 0 ∞ P ¯ ( k ) x k 표시({style {\frac {1}{\theta _{4}(x)}=\frac _{n=1}^{\infty}{\frac {1+x^{n}}{1-x^{n}}=\sum _{k=0}^{\infty}{\overline{P}(k)^{k}}}{k^{k}}}}}}를 표시합니다. 1 θ 4 ( x ) = 1 + 2 x + 4 x 2 + 8 x 3 + 14 x 4 + 24 x 5 + 40 x 6 + 64 x 7 + 100 x 8 + 154 x 9 + 232 x 10 + … 표시({style\frac {1}{\theta _{4}(x)}=1+2x+4x^{2}+8x^{3}+14x^{4}+24x^{5}+40x^{6}+64x^{7}+100x^{8}+154x^{9}+232x^{10}+\deta} 만약, 주어진 숫자 k에 대해, 모든 파티션이 합치 크기가 결코 증가하지 않는 방식으로 설정되어 있고, 자신의 왼쪽에 같은 크기의 합치가 없는 모든 합치는 이 유형의 각 파티션에 대해 표시될 수 있다,그러면 k{display}에 따라 표시된 파티션의 결과 수[27]가 됩니다 오버파티션 ¯ k ) displaystyle {\overline {P}(k)} 스타일
첫 번째 예:
P ¯ ( 4 ) = 14 {\style {P}(4)=14} 표시 다음 14가지 파티션 표시 가능성은 합계 4에 대해 존재합니다.
(4), (4 ), (3+1), (3 +1), (3+1 ), (3 +1 ), (2+2), (2 +2), (2+1+1), (2 +1+1), (2+1 +1), (2 +1 +1), (1+1+1+1), (1 +1+1+1)
두 번째 예:
P ¯ ( 5 ) = 24 {\style {P}(5)=24} 표시 다음과 같은 24가지 파티션 표시 가능성이 합계 5에 대해 존재합니다.
(5), (5 ), (4+1), (4 +1), (4+1 ), (4 +1 ), (3+2), (3 +2), (3+2 ), (3 +2 ), (3+1+1), (3 +1+1), (3+1 +1), (3 +1 +1), (2+2+1), (2 +2+1), (2+2+1 ), (2 +2+1 ), (2+1+1+1), (2 +1+1+1), (2+1 +1+1), (2 +1 +1+1), (1+1+1+1+1), (1 +1+1+1+1)
파티션 번호 시퀀스 간의 관계 정수열 온라인 백과사전(OEIS)에서 정규 파티션 번호 P(n) {\displaystyle P(n)}의 순서는 코드 A000041 아래에 있고, 엄격한 파티션의 순서는 코드 A000009 아래에 Q(n) {\displaystyle Q(n)}이고, 코드 A015128 아래에 있는 슈퍼 파티션 P(n)의 순서는 라인 {P}(n) 위에 있다. 인덱스 = 1 displaystyle 1}
슈퍼 파티션 ¯ n displaystyle {overline {P}(n)} [28] [29]
P ¯ ( n ) = ∑ k = 0 n P ( n − k ) Q ( k ) {\style {\overline {P}(n)=\sum _{k=0}^{n}P(n-k)Q(k)} 표시 다음 숫자 순서 표에서 이 공식을 예로 사용해야 합니다.
n P(n) Q(n) P ¯ ( n ) {\style {P}(n)} 표시 0 1 1 1 = 1*1 1 1 1 2 = 1 * 1 + 1 * 1 2 2 1 4 = 2 * 1 + 1 * 1 + 1 * 1 3 3 2 8 = 3 * 1 + 2 * 1 + 1 * 1 + 1 * 2 4 5 2 14 = 5 * 1 + 3 * 1 + 2 * 1 + 1 * 2 + 1 * 2 5 7 3 24 = 7 * 1 + 5 * 1 + 3 * 1 + 2 * 2 + 1 * 2 + 1 * 3
이 속성과 관련하여 함수01 ϑ를 통해 다음과 같은 두 계열의 합계 조합을 설정할 수도 있습니다.
θ 4 ( x ) = [ ∑ k = 0 ∞ P ( k ) x k ] − 1 [ ∑ k = 0 ∞ Q ( k ) x k ] − 1 {\displaystyle \theta _{4}(x)=displaybiggl [}\sum _{k=0}^{\infty}P(k)x^{k}{\biggr}}{\biggl [}\sum _{k=0}^{\infty}Q(k)x^{\biggr}}^{-1}}} 메모들 ^ 예: https://dlmf.nist.gov/20.1 을 참조하십시오.일반적으로 이는 z{displaystyle 스트립 외부 있을 (ez ) α = α γ z{\ alpha operatorname {Log} e^{z}) = e ^{\ alpha operatorname {Log ^{ }} , 로그 displaystyle \operatorname {Log} 복소 로그의 주 분기를 나타냅니다.^ q 1 {{displaystyle <1 모든 q C displaystyle q\in \mathbb {C} ( q ) = 0 {{displaystyle \theta {1}(q }.
레퍼런스 ^ Tyurin, Andrey N. (30 October 2002). "Quantization, Classical and Quantum Field Theory and Theta-Functions". arXiv :math/0210466v1 ^ Chang, Der-Chen (2011). Heat Kernels for Elliptic and Sub-elliptic Operators . Birkhäuser. p. 7. ^ Tata Lectures on Theta I doi :10.1007/978-0-8176-4577-9 . ISBN 978-0-8176-4572-4 ^ "A002103 - OEIS" . Retrieved 2023-05-28 .^ "Series Expansion of EllipticNomeQ differs from older Mathematica Version" . Retrieved 2023-05-28 .^ R. B. King, E. R. Canfield (1992-08-01), "Icosahedral symmetry and the quintic equation", Computers & Mathematics with Applications , vol. 24, no. 3, pp. 13–28, doi :10.1016/0898-1221(92)90210-9 ISSN 0898-1221 ^ Adolf Kneser (1927), "Neue Untersuchung einer Reihe aus der Theorie der elliptischen Funktionen." , Journal für die reine und angewandte Mathematik , vol. 158, pp. 209–218, ISSN 0075-4102 , retrieved 2023-06-11 ^ D. K. Lee (1989-03-01), Application of theta functions for numerical evaluation of complete elliptic integrals of the first and second kinds doi :10.2172/6137964 , OSTI 6137964 , retrieved 2023-06-11 ^ K. H. Schellbach (1864), Die Lehre von den elliptischen Integralen und den Theta-Functionen , retrieved 2023-06-06 ^ Yi, Jinhee (2004). "Theta-function identities and the explicit formulas for theta-function and their applications" . Journal of Mathematical Analysis and Applications . 292 (2): 381–400. doi :10.1016/j.jmaa.2003.12.009 ^ Berndt, Bruce C; Rebák, Örs (9 January 2022). "Explicit Values for Ramanujan's Theta Function ϕ(q)" . Hardy-Ramanujan Journal . 44 : 8923. doi :10.46298/hrj.2022.8923 S2CID 245851672 . ^ Yi, Jinhee (15 April 2004). "Theta-function identities and the explicit formulas for theta-function and their applications" . Journal of Mathematical Analysis and Applications . 292 (2): 381–400. doi :10.1016/j.jmaa.2003.12.009 ^ Andreas Diekmann: 무한 제품 무한 합계 무한 타원형 세타. 물리학 연구소 본, 아브루팜 1. 2021년 10월 ^ Landau (1899) zitiert nach Borwein , 94페이지, 연습 3 ^ "Number-theoretical, combinatorial and integer functions – mpmath 1.1.0 documentation" . Retrieved 2021-07-18 .^ Mező, István (2013), "Duplication formulae involving Jacobi theta functions and Gosper's q -trigonometric functions", Proceedings of the American Mathematical Society 141 (7): 2401–2410, doi :10.1090/s0002-9939-2013-11576-5 ^ Mező, István (2012). "A q -Raabe formula and an integral of the fourth Jacobi theta function" . Journal of Number Theory . 133 (2): 692–704. doi :10.1016/j.jnt.2012.08.025 ^ Weisstein, Eric W. "Elliptic Alpha Function" . MathWorld ^ "integration - Curious integrals for Jacobi Theta Functions $\int_0^1 \vartheta_n(0,q)dq$" . 2022-08-13.^ Ohyama, Yousuke (1995). "Differential relations of theta functions" . Osaka Journal of Mathematics . 32 (2): 431–450. ^ 시무라, 반 적분 중량의 모듈식 형태 ^ "Elliptic Integral Singular Value" . Retrieved 2023-04-07 .^ https://www.researchgate.net/publication/235432739_Ramanujan%27s_theta-function_identities_involving_Lambert_series [베어 ^ "code golf - Strict partitions of a positive integer" . Retrieved 2022-03-09 .^ "A000009 - OEIS" . 2022-03-09.^ https://www.math.lsu.edu/ ~mahlburg/preprints/4.pdf [베어 URL ^ Kim, Byungchan (28 April 2009). "Elsevier Enhanced Reader" . Discrete Mathematics . 309 (8): 2528–2532. doi :10.1016/j.disc.2008.05.007 ^ Eric W. Weisstein (2022-03-11). "Partition Function P" . ^ Eric W. Weisstein (2022-03-11). "Partition Function Q" . Abramowitz, Milton ; Stegun, Irene A. (1964). Handbook of Mathematical Functions Dover Publications . sec. 16.27ff. ISBN 978-0-486-61272-0 Akhiezer, Naum Illyich (1990) [1970]. Elements of the Theory of Elliptic Functions . AMS Translations of Mathematical Monographs. Vol. 79. Providence, RI: AMS . ISBN 978-0-8218-4532-5 Farkas, Hershel M. ; Kra, Irwin (1980). Riemann Surfaces . New York: Springer-Verlag . ch. 6. ISBN 978-0-387-90465-8 리만 세타 치료용 )Hardy, G. H. ; Wright, E. M. (1959). An Introduction to the Theory of Numbers (4th ed.). Oxford: Clarendon Press .Mumford, David (1983). Tata Lectures on Theta I . Boston: Birkhauser . ISBN 978-3-7643-3109-2 Pierpont, James (1959). Functions of a Complex Variable . New York: Dover Publications .Rauch, Harry E. ; Farkas, Hershel M. (1974). Theta Functions with Applications to Riemann Surfaces . Baltimore: Williams & Wilkins . ISBN 978-0-683-07196-2 Reinhardt, William P.; Walker, Peter L. (2010), "Theta Functions" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 Whittaker, E. T. ; Watson, G. N. (1927). A Course in Modern Analysis (4th ed.). Cambridge: Cambridge University Press . ch. 21.(Jacobi의 θ 함수의 역사) 진일보한 내용 해리 라우치와 허셜 M. 파르카스: 세타는 리만 서피스, 윌리엄스 및 윌킨스, 볼티모어 MD 1974, ISBN 0-683-07196-3 에 대한 응용 프로그램으로 작동합니다.
찰스 에르미트: Surarésolution de l'Equation ducinquiéme degré Competesrendus, C. R. Acad. 1858년 3월 11일, 과학자 파리. 외부 링크 이 기사는 크리에이티브 커먼즈 어트리뷰션/쉐어라이크 라이선스 로 라이센스가 부여된 PlanetMath 의 Jacobi theta 함수의 적분 표현에서 얻은 자료를 통합합니다.




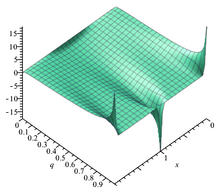
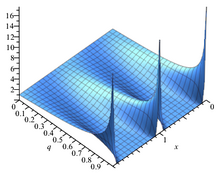










 리우빌의 정리에서 요구하는 대로 무한합니다.
리우빌의 정리에서 요구하는 대로 무한합니다.
![{\displaystyle {\begin{aligned}\vartheta _{01}(z;\tau )&=\vartheta \left(z+{\tfrac {1}{2}};\tau \right)\\[3pt]\vartheta _{10}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi iz\right)\vartheta \left(z+{\tfrac {1}{2}}\tau ;\tau \right)\\[3pt]\vartheta _{11}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi i\left(z+{\tfrac {1}{2}}\right)\right)\vartheta \left(z+{\tfrac {1}{2}}\tau +{\tfrac {1}{2}};\tau \right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee051ca15813825e13589298c0efd02e3f68e0cf)










![{\displaystyle k'(\tau )={\sqrt {1-k^{2}}}={\biggl \{}{\theta _{4}[q(k)] \over \theta _{3}[q(k)]}{\biggr \}}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c5d69f712332e32a0575efa0eb2df2b29ee0fb1)
![{\displaystyle q(k)=\exp {\biggl [}-\pi \,{\frac {K({\sqrt {1-k^{2}}})}{K(k)}}{\biggr ]}=\exp {\biggl [}-\pi \,{\frac {K'(k)}{K(k)}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/836d211708067132c0a682f98e9a7355d463366b)
![{\displaystyle \theta _{3}[q(k)]={\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5de1ea9f13775acb606c8cb4c2c8268c77ad546)
![{\displaystyle \theta _{4}[q(k)]={\sqrt[{4}]{1-k^{2}}}\,{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b18cb501a0e5521687946e420015ea2bfb8e9367)
![{\displaystyle \theta _{2}[q(k)]=|k|^{1/2}{\sqrt {2\pi ^{-1}K(k)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29e3c3bf629e5d0c9de740935c11e79b713f1e69)

![{\displaystyle K(k)={\frac {\pi }{2}}\sum _{a=0}^{\infty }{\frac {[(2a)!]^{2}}{16^{a}(a!)^{4}}}k^{2a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91ea0da33be9e1a79cff559e92a2acab4b6702c0)
![{\displaystyle {\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}={\frac {\theta _{3}[q(k)]-\theta _{4}[q(k)]}{\theta _{3}[q(k)]+\theta _{4}[q(k)]}}={\biggl [}\sum _{n=1}^{\infty }2\,q(k)^{(2n-1)^{2}}{\biggr ]}{\biggl [}1+\sum _{n=1}^{\infty }2\,q(k)^{4n^{2}}{\biggr ]}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5500425d0ada42472a8c28e6966d0337f437e816)
![{\displaystyle q(k)=\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {1-{\sqrt[{4}]{1-k^{2}}}}{1+{\sqrt[{4}]{1-k^{2}}}}}{\biggr )}^{4n-3}={\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n)}{2^{4n-3}}}{\biggl (}{\frac {k}{1+{\sqrt {1-k^{2}}}}}{\biggr )}^{4n-3}{\biggr ]}^{2}=k^{2}{\biggl \{}{\frac {1}{2}}+{\biggl [}\sum _{n=1}^{\infty }{\frac {{\text{Sc}}(n+1)}{2^{4n+1}}}k^{2n}{\biggr ]}{\biggr \}}^{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64e5aaa2ec52c1e6c5b4a0b5bfb2178f3fe1dd76)

![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{\text{Sc(n)}}}=16}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb3a854313f8dcb943617886a159fa767f326382)












 이 방정식의 도함수는 Kneser 수열의
이 방정식의 도함수는 Kneser 수열의 


![{\displaystyle \mathrm {Sc} (4)={\frac {2}{3}}\sum _{m=1}^{3}\mathrm {Sc} (m)\,\mathrm {Kn} (4-m)={\frac {2}{3}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c0e2f6c8f1e9bd5a3f5eb70920b4d90fff4bc48)

![{\displaystyle \mathrm {Sc} (5)={\frac {2}{4}}\sum _{m=1}^{4}\mathrm {Sc} (m)\,\mathrm {Kn} (5-m)={\frac {2}{4}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bb6c5b6b9b4e5d44f245fc6b05b5e3b5ddb4b25)

![{\displaystyle \mathrm {Sc} (6)={\frac {2}{5}}\sum _{m=1}^{5}\mathrm {Sc} (m)\,\mathrm {Kn} (6-m)={\frac {2}{5}}{\bigl [}{\color {navy}\mathrm {Sc} (1)}\,{\color {cornflowerblue}\mathrm {Kn} (5)}+{\color {navy}\mathrm {Sc} (2)}\,{\color {cornflowerblue}\mathrm {Kn} (4)}+{\color {navy}\mathrm {Sc} (3)}\,{\color {cornflowerblue}\mathrm {Kn} (3)}+{\color {navy}\mathrm {Sc} (4)}\,{\color {cornflowerblue}\mathrm {Kn} (2)}+{\color {navy}\mathrm {Sc} (5)}\,{\color {cornflowerblue}\mathrm {Kn} (1)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1331a9d6e16d802ebaf5eb68d2d9724296a7f64)


![{\displaystyle {\begin{aligned}\vartheta _{00}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{00}(z;\tau )\quad &\vartheta _{01}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{10}(z;\tau )\\[3pt]\vartheta _{10}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{01}(z;\tau )\quad &\vartheta _{11}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=-i\alpha \,\vartheta _{11}(z;\tau ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e38521d263e968c6643113cb856744c3d8417638)
![{\displaystyle {\begin{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n}q^{n^{2}}\quad &\vartheta _{01}(w,q)&=\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n}q^{n^{2}}\\[3pt]\vartheta _{10}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}\quad &\vartheta _{11}(w,q)&=i\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acbc490b1dd786cc2ef221b6b0834661d3f41ac3)






![{\displaystyle {\begin{aligned}\vartheta _{01}(z\mid q)&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right),\\[3pt]\vartheta _{10}(z\mid q)&=2q^{\frac {1}{4}}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right),\\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac {1}{4}}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2f486ca65bf1df31851e9591220ff601cf6fb0)


![{\displaystyle {\begin{aligned}\vartheta _{00}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{01}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{10}(z;\tau )&=-ie^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{11}(z;\tau )&=e^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd32c29ab16bda39187ec29c1169e8019bcb54af)
 (를) 적분 항등식으로 사용합니다.
(를) 적분 항등식으로 사용합니다.![{\displaystyle \theta _{3}(q)=1+{\frac {4q{\sqrt {\ln(1/q)}}}{\sqrt {\pi }}}\int _{0}^{\infty }{\frac {\exp[-\ln(1/q)\,x^{2}]\{1-q^{2}\cos[2\ln(1/q)\,x]\}}{1-2q^{2}\cos[2\ln(1/q)\,x]+q^{4}}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e26186736a2e273adfa2732fea7ee65263231d4)
![{\displaystyle {\biggl [}{\frac {2}{\pi }}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}{\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-\pi ){\bigr ]}=1+4\exp(-\pi )\int _{0}^{\infty }{\frac {\exp(-\pi x^{2})[1-\exp(-2\pi )\cos(2\pi x)]}{1-2\exp(-2\pi )\cos(2\pi x)+\exp(-4\pi )}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/942b823ba5f2a5d89016b6493ca9cc3b187cb86f)
![{\displaystyle {\biggl [}{\frac {2}{\pi }}K({\sqrt {2}}-1){\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{2}}\exp(-{\sqrt {2}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {2}}\,\pi x^{2})[1-\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)]}{1-2\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)+\exp(-4{\sqrt {2}}\,\pi )}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cc3a6cd1621989208f56af90722f5230eecf7b6)
![{\displaystyle {\biggl \{}{\frac {2}{\pi }}K{\bigl [}\sin {\bigl (}{\frac {\pi }{12}}{\bigr )}{\bigr ]}{\biggr \}}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {3}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{3}}\exp(-{\sqrt {3}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {3}}\,\pi x^{2})[1-\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)]}{1-2\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)+\exp(-4{\sqrt {3}}\,\pi )}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d462b60e5965c30acaf2837ae9770eb3a3560f5)

 표시되어야 합니다.
표시되어야 합니다.![{\displaystyle \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{2^{n^{2}}}}=1+2\pi ^{-1/2}{\sqrt {\ln(2)}}\int _{0}^{\infty }{\frac {\exp[-\ln(2)\,x^{2}]\{16-4\cos[2\ln(2)\,x]\}}{17-8\cos[2\ln(2)\,x]}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ae1d7b2a53c1af22b4bd823a8ca710f4c9a542)

![{\displaystyle \theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{3^{n^{2}}}}=1+{\frac {4}{3}}\pi ^{-1/2}{\sqrt {\ln(3)}}\int _{0}^{\infty }{\frac {\exp[-\ln(3)\,x^{2}]\{81-9\cos[2\ln(3)\,x]\}}{82-18\cos[2\ln(3)\,x]}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/435997da103ea29c5f3136563c5f98b73a2ec986)




![{\displaystyle {\begin{aligned}\varphi \left(e^{-\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}={\sqrt {2}}\,\eta \left({\sqrt {-1}}\right)\\\varphi \left(e^{-2\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {2+{\sqrt {2}}}}{2}}\\\varphi \left(e^{-3\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {1+{\sqrt {3}}}}{\sqrt[{8}]{108}}}\\\varphi \left(e^{-4\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {2+{\sqrt[{4}]{8}}}{4}}\\\varphi \left(e^{-5\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {2+{\sqrt {5}}}{5}}}\\\varphi \left(e^{-6\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}}}{\sqrt[{8}]{12^{3}}}}\\\varphi \left(e^{-7\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}}}{{\sqrt[{8}]{14^{3}}}\cdot {\sqrt[{16}]{7}}}}\\\varphi \left(e^{-8\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2+{\sqrt {2}}}}+{\sqrt[{8}]{128}}}{4}}\\\varphi \left(e^{-9\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {1+{\sqrt[{3}]{2+2{\sqrt {3}}}}}{3}}\\\varphi \left(e^{-10\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{64}}+{\sqrt[{4}]{80}}+{\sqrt[{4}]{81}}+{\sqrt[{4}]{100}}}}{\sqrt[{4}]{200}}}\\\varphi \left(e^{-11\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {4+{\sqrt {11}}-3{\sqrt {3}}\tanh \left({\tfrac {1}{4}}\operatorname {arcosh} \left({\tfrac {7}{4}}\right)+{\tfrac {1}{6}}\operatorname {artanh} \left({\tfrac {27}{47}}{\sqrt {3}}\right)\right)}{{\sqrt[{8}]{44}}\cdot {\sqrt {-66+22{\sqrt {11}}}}}}\\\varphi \left(e^{-12\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{2}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{24}}}}{2{\sqrt[{8}]{108}}}}\\\varphi \left(e^{-13\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {-{\tfrac {1}{13}}+{\tfrac {2}{13}}{\sqrt {3}}\coth \left({\tfrac {1}{6}}\operatorname {artanh} \left({\tfrac {6}{11}}{\sqrt {3}}\right)\right)}}\\\varphi \left(e^{-14\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}+{\sqrt {10+2{\sqrt {7}}}}+{\sqrt[{8}]{28}}{\sqrt {4+{\sqrt {7}}}}}}{\sqrt[{16}]{28^{7}}}}\\\varphi \left(e^{-15\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {7+3{\sqrt {3}}+{\sqrt {5}}+{\sqrt {15}}+{\sqrt[{4}]{60}}+{\sqrt[{4}]{1500}}}}{{\sqrt[{8}]{12^{3}}}\cdot {\sqrt {5}}}}\\2\varphi \left(e^{-16\pi }\right)&=\varphi \left(e^{-4\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt[{4}]{1+{\sqrt {2}}}}{\sqrt[{16}]{128}}}\\\varphi \left(e^{-17\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2}}(1+{\sqrt[{4}]{17}})+{\sqrt[{8}]{17}}{\sqrt {5+{\sqrt {17}}}}}{\sqrt {17+17{\sqrt {17}}}}}\\2\varphi \left(e^{-20\pi }\right)&=\varphi \left(e^{-5\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {3+2{\sqrt[{4}]{5}}}{5{\sqrt {2}}}}}\\6\varphi \left(e^{-36\pi }\right)&=3\varphi \left(e^{-9\pi }\right)+2\varphi \left(e^{-4\pi }\right)-\varphi \left(e^{-\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt[{3}]{{\sqrt[{4}]{2}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{216}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a627defe4dea84f0768aeb79994af937788f645)


![{\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{5}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{5}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{5}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087f2996a1cad31a875a6346e7b52be98453668f)
![{\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{7}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{7}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f01f0cb2fd209abfbb1ac4c204c509f2b3f47b74)
![{\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{9}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{9}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51aea624bd4ccfed27077389532d4b07efda771e)
![{\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{11}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {5}{11}}{\sqrt {2}}\,\varpi {\bigr )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3839f652515fbc383f7fa265b6541beaa7582c59)

![{\displaystyle {\begin{aligned}2\varphi \left(q^{4}\right)&=\varphi (q)+{\sqrt {2\varphi ^{2}\left(q^{2}\right)-\varphi ^{2}(q)}}\\3\varphi \left(q^{9}\right)&=\varphi (q)+{\sqrt[{3}]{9{\frac {\varphi ^{4}\left(q^{3}\right)}{\varphi (q)}}-\varphi ^{3}(q)}}\\{\sqrt {5}}\varphi \left(q^{25}\right)&=\varphi \left(q^{5}\right)\cot \left({\frac {1}{2}}\arctan \left({\frac {2}{\sqrt {5}}}{\frac {\varphi (q)\varphi \left(q^{5}\right)}{\varphi ^{2}(q)-\varphi ^{2}\left(q^{5}\right)}}{\frac {1+s(q)-s^{2}(q)}{s(q)}}\right)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3a018fbcd1409ba1ebb0c85d8178fb163fa3ba0)

![{\displaystyle {\begin{aligned}s(q)&={\sqrt[{5}]{\tan \left({\frac {1}{2}}\arctan \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)\cot ^{2}\left({\frac {1}{2}}\operatorname {arccot} \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)}}\\&={\cfrac {e^{-\pi i/(25\tau )}}{1-{\cfrac {e^{-\pi i/(5\tau )}}{1+{\cfrac {e^{-2\pi i/(5\tau )}}{1-\ddots }}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de23ddbf5b96a5a2470d73ba10f05153d2a7e37d)
![{\displaystyle {\begin{array}{lll}\varphi \left(\exp(-{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\\\varphi \left(\exp(-2{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\cos({\tfrac {1}{24}}\pi )\\\varphi \left(\exp(-3{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{7/8}({\sqrt[{3}]{2}}+1)\\\varphi \left(\exp(-4{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-5/3}3^{13/8}{\Bigl (}1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{5/8}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/913e0c2a4e7f8efd215821d4423789caf3cc7382)
![{\displaystyle {\begin{array}{lll}\varphi \left(\exp(-{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{7/8}\\\varphi \left(\exp(-2{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{1/8}{\Bigl (}1+{\sqrt {{\sqrt {2}}-1}}{\Bigr )}\\\varphi \left(\exp(-3{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{3/8}3^{-1/2}({\sqrt {3}}+1){\sqrt {\tan({\tfrac {5}{24}}\pi )}}\\\varphi \left(\exp(-4{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{-1/8}{\Bigl (}1+{\sqrt[{4}]{2{\sqrt {2}}-2}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{15/8}\\&&\cdot {\biggl (}{\tfrac {1}{5}}{\sqrt {3}}\cos({\tfrac {1}{10}}\pi ){\dfrac {{(9+{\sqrt {6}})}^{1/3}(1+{\sqrt {3}})+{\sqrt {2}}~3^{1/6}5^{1/3}}{({9+{\sqrt {6}}})^{1/3}(1+{\sqrt {3}})-{\sqrt {2}}~{3^{1/6}5^{1/3}}}}-{\tfrac {1}{5}}({\sqrt {5}}+{\sqrt {2}})\sin({\tfrac {1}{5}}\pi ){\biggr )}\\\varphi \left(\exp(-{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{-13/24}3^{-1/8}{\sqrt {\sin({\tfrac {5}{12}}\pi )}}\\\varphi \left(\exp(-{\tfrac {1}{2}}{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{5/24}3^{-1/8}\sin({\tfrac {5}{24}}\pi )\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8feecfd935ff166f01edbac18a95c490086040f0)
![{\displaystyle \theta _{2}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}-\theta _{4}(q)^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49fdbf249a5c77891ea7be62a7abdb74bfca9c20)
![{\displaystyle \theta _{3}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}+\theta _{4}(q)^{2}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab78a4868b53c96cb965bc889ba12f8e4fd5bd44)


![{\displaystyle 27\,\theta _{3}(q^{3})^{8}-18\,\theta _{3}(q^{3})^{4}\theta _{3}(q)^{4}-\,\theta _{3}(q)^{8}=8\,\theta _{3}(q^{3})^{2}\theta _{3}(q)^{2}[2\,\theta _{4}(q)^{4}-\theta _{3}(q)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee8b22b2491acbf41acf156847592744fe5efda4)
![{\displaystyle 27\,\theta _{4}(q^{3})^{8}-18\,\theta _{4}(q^{3})^{4}\theta _{4}(q)^{4}-\,\theta _{4}(q)^{8}=8\,\theta _{4}(q^{3})^{2}\theta _{4}(q)^{2}[2\,\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6db22a825f23c8747194677df1ba5b9cd6776c58)
![{\displaystyle [\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}][5\,\theta _{3}(q^{5})^{2}-\theta _{3}(q)^{2}]^{5}=256\,\theta _{3}(q^{5})^{2}\theta _{3}(q)^{2}\theta _{4}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21698abd5cd7e4f2b57023ecd5dd70b3fd545ffb)
![{\displaystyle [\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}][5\,\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}]^{5}=256\,\theta _{4}(q^{5})^{2}\theta _{4}(q)^{2}\theta _{3}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bc5563a31bcb890a22ebb282ad224297a82b287)
![{\displaystyle {\biggl [}{\frac {\theta _{3}(q^{1/3})^{2}}{\theta _{3}(q)^{2}}}-{\frac {3\,\theta _{3}(q^{3})^{2}}{\theta _{3}(q)^{2}}}{\biggr ]}^{2}=4-4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{4}(q)^{2}}{\theta _{3}(q)^{4}}}{\biggr ]}^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a41eb7bba4644993c0994d693977d751526d68a1)
![{\displaystyle {\biggl [}{\frac {3\,\theta _{4}(q^{3})^{2}}{\theta _{4}(q)^{2}}}-{\frac {\theta _{4}(q^{1/3})^{2}}{\theta _{4}(q)^{2}}}{\biggr ]}^{2}=4+4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{3}(q)^{2}}{\theta _{4}(q)^{4}}}{\biggr ]}^{2/3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4d0741127e031b7079dffa001160094eb9b03c9)
![{\displaystyle R(q)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/122911c8d5591255a99de086a6643e60e8496af8)
![{\displaystyle R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87bef51d2716d70a8054cd882a9c6a98aa234b16)
![{\displaystyle R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fd8befdabb6ac82b6c4fff8f0a5bb89a1a5ac55)
![{\displaystyle S(x)={\frac {R(q^{4})}{R(q^{2})R(q)}}=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92dbdbb7e293d5683998a2e45889e3a7920b4a0f)
![{\displaystyle {\frac {\theta _{3}(q^{1/5})}{\theta _{3}(q^{5})}}-1={\frac {1}{S(q)}}{\bigl [}S(q)^{2}+R(q^{2}){\bigr ]}{\bigl [}1+R(q^{2})S(q){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1f9826acfe6b0205eb7dec745ce83aae7e6d01)
![{\displaystyle 1-{\frac {\theta _{4}(q^{1/5})}{\theta _{4}(q^{5})}}={\frac {1}{R(q)}}{\bigl [}R(q^{2})+R(q)^{2}{\bigr ]}{\bigl [}1-R(q^{2})R(q){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb6fd08483ead704a199a261edcf54d483835ad9)
![{\displaystyle \theta _{3}(q^{1/5})^{2}-\theta _{3}(q)^{2}={\bigl [}\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}{\bigr ]}{\biggl [}1+{\frac {1}{R(q^{2})S(q)}}+R(q^{2})S(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}+{\frac {1}{S(q)}}-S(q){\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87e7c0cdbc5280e1ca49f87d77c2924e364d6c6)
![{\displaystyle \theta _{4}(q)^{2}-\theta _{4}(q^{1/5})^{2}={\bigl [}\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}{\bigr ]}{\biggl [}1-{\frac {1}{R(q^{2})R(q)}}-R(q^{2})R(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}-{\frac {1}{R(q)}}+R(q){\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e4601790cf31b8e82943713c410b532e4d75980)
![{\displaystyle \theta _{4}[q(k)]=\theta _{4}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ece5e6b2598db08419e115b84fa8dc058e3980b8)
![{\displaystyle \theta _{4}[q(k)^{2}]=\theta _{3}[q(k)]{\sqrt[{8}]{1-k^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85cc179f3c7fab7e4f664ea3a9ad3bed2c751a65)
![{\displaystyle \theta _{3}[q(k)^{2}]=\theta _{3}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0b0e95b8b6fd152fc74a01c0f7fbab2b9a6555)
![{\displaystyle \theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(t^{3}){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {t^{4}-t^{2}+1}}-t^{2}+2}}+{\sqrt {t^{2}+1}}\,{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0608e409cfd0018afa26a9e4561bc8ce04b7c964)


![{\displaystyle \theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(1){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(1){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {3}}+{\sqrt {2}}\,{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27d9399dd8871346e454374d0965a18caba1db5c)
![{\displaystyle \theta _{4}{\bigl [}\exp(-3{\sqrt {2}}\,\pi ){\bigr ]}=\theta _{4}{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}\,3^{-1/2}{\bigl (}{\sqrt {3}}+{\sqrt {2}}\,{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d24c901354972a0b0861ecf1304c11b74666f25b)

![{\displaystyle \theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ^{-6}){\bigr ]}{\bigr \}}^{3}{\biggr \rangle }=\theta _{4}{\biggl \langle }q{\bigl \{}\tan {\bigl [}{\tfrac {1}{2}}\arctan(\Phi ^{-6}){\bigr ]}{\bigr \}}{\biggr \rangle }\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {\Phi ^{-8}-\Phi ^{-4}+1}}-\Phi ^{-4}+2}}+{\sqrt {\Phi ^{-4}+1}}\,{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dc07d14cd349f46b4f18689ce8fc44277e67902)
![{\displaystyle \theta _{4}{\bigl [}\exp(-3{\sqrt {10}}\,\pi ){\bigr ]}=\theta _{4}{\bigl [}\exp(-{\sqrt {10}}\,\pi ){\bigr ]}\,3^{-1/2}{\bigl (}{\sqrt {2{\sqrt {\Phi ^{-8}-\Phi ^{-4}+1}}-\Phi ^{-4}+2}}+{\sqrt {\Phi ^{-4}+1}}\,{\bigr )}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76245ff2f6bee7a43882f3f4ebbcad691b406a96)
 정확하게 나타냅니다
정확하게 나타냅니다

![{\displaystyle ={\frac {\sqrt {5}}{4}}\,\theta _{2}(\Phi ^{-2})^{2}={\frac {\sqrt {5}}{8}}{\bigl [}\theta _{3}(\Phi ^{-1})^{2}-\theta _{4}(\Phi ^{-1})^{2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e05e65a1d4c792ec63055ed7d1d9a08f7faf285e)
![{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}={\frac {\sqrt {5}}{4}}\,{\biggl [}\sum _{n=1}^{\infty }2\,\Phi ^{-(2n-1)^{2}/2}{\biggr ]}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0218550f8623ef9dce9705bde847639ee6e6919)

![{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}^{2}}}={\frac {5}{24}}{\bigl [}2\,\theta _{2}(\Phi ^{-2})^{4}-\theta _{3}(\Phi ^{-2})^{4}+1{\bigr ]}={\frac {5}{24}}{\bigl [}\theta _{3}(\Phi ^{-2})^{4}-2\,\theta _{4}(\Phi ^{-2})^{4}+1{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71c7f301cb452442a43e1fcd9c91ea78bc820ef9)
![{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{P_{2n-1}}}={\frac {1}{\sqrt {2}}}\,\theta _{2}{\bigl [}({\sqrt {2}}-1)^{2}{\bigr ]}^{2}={\frac {1}{2{\sqrt {2}}}}{\bigl [}\theta _{3}({\sqrt {2}}-1)^{2}-\theta _{4}({\sqrt {2}}-1)^{2}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25a2e2b5ff5d3f65182b77f5be772944bc4d6ea2)
![{\displaystyle {\begin{aligned}\theta _{4}^{2}(q)&=iq^{\frac {1}{4}}\sum _{k=-\infty }^{\infty }q^{2k^{2}-k}\theta _{1}\left({\frac {2k-1}{2i}}\ln q,q\right),\\[6pt]\theta _{4}^{2}(q)&=\sum _{k=-\infty }^{\infty }q^{2k^{2}}\theta _{4}\left({\frac {k\ln q}{i}},q\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/428f8073ad45e4e54778db88a3dbb2f5b0ab1f30)


![{\displaystyle {\begin{aligned}\vartheta (z;\tau )=\vartheta _{00}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}+{\frac {\tau }{2}}\\[3pt]\vartheta _{11}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau \\[3pt]\vartheta _{10}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {1}{2}}\\[3pt]\vartheta _{01}(z;\tau )&=0\quad &\Longleftrightarrow &&\quad z&=m+n\tau +{\frac {\tau }{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcdb60358dddb241ffda786440efa91cc0844ca9)




![{\displaystyle {\begin{aligned}\theta _{2}(q)=\vartheta _{10}(0;\tau )&={\frac {2\eta ^{2}(2\tau )}{\eta (\tau )}},\\[3pt]\theta _{3}(q)=\vartheta _{00}(0;\tau )&={\frac {\eta ^{5}(\tau )}{\eta ^{2}\left({\frac {1}{2}}\tau \right)\eta ^{2}(2\tau )}}={\frac {\eta ^{2}\left({\frac {1}{2}}(\tau +1)\right)}{\eta (\tau +1)}},\\[3pt]\theta _{4}(q)=\vartheta _{01}(0;\tau )&={\frac {\eta ^{2}\left({\frac {1}{2}}\tau \right)}{\eta (\tau )}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2358dd2d333a2740823f158700af932d247a2c7e)




![{\displaystyle E(k)={\frac {\pi }{2}}\sum _{a=0}^{\infty }{\frac {[(2a)!]^{2}}{(1-2a)16^{a}(a!)^{4}}}k^{2a}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a4e8c4e1616502c6de3e16bb661c1372b93c0fd)



![{\displaystyle \theta _{2}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{2}(x)={\frac {1}{2\pi x}}\theta _{2}(x)\theta _{3}(x)^{2}E{\biggl [}{\frac {\theta _{2}(x)^{2}}{\theta _{3}(x)^{2}}}{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a311084c05bdae1b514737c2f0108933b9f8bae)
![{\displaystyle \theta _{3}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{3}(x)=\theta _{3}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\theta _{3}(x)^{2}-\theta _{4}(x)^{2}}{\theta _{3}(x)^{2}+\theta _{4}(x)^{2}}}{\biggr ]}-{\frac {\theta _{4}(x)^{2}}{4\,x}}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/104d1b3737a0be4eda8a3a1e245186de9134a6e9)
![{\displaystyle \theta _{4}'(x)={\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x)=\theta _{4}(x){\bigl [}\theta _{3}(x)^{2}+\theta _{4}(x)^{2}{\bigr ]}{\biggl \{}{\frac {1}{2\pi x}}E{\biggl [}{\frac {\theta _{3}(x)^{2}-\theta _{4}(x)^{2}}{\theta _{3}(x)^{2}+\theta _{4}(x)^{2}}}{\biggr ]}-{\frac {\theta _{3}(x)^{2}}{4\,x}}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5be9c018c56615a9085df89d3db2ca5d7d26b5)
![{\displaystyle \vartheta _{4}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\vartheta _{3}(x){\biggr ]}-\vartheta _{3}(x){\biggl [}{\frac {\mathrm {d} }{\mathrm {d} x}}\,\theta _{4}(x){\biggr ]}={\frac {1}{4\,x}}\,\theta _{3}(x)\,\theta _{4}(x){\bigl [}\theta _{3}(x)^{4}-\theta _{4}(x)^{4}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88237a98911175d2efc60c4d21094300a862abd)

















 (는)
(는) 


 n차원 복소 벡터이며, 초첨자 T는
n차원 복소 벡터이며, 초첨자 T는 







![{\displaystyle {\frac {4^{-1/(n+2)}}{n+2}}\csc {\bigl (}{\frac {\pi }{n+2}}{\bigr )}\beta {\biggl [}{\frac {n}{2(n+2)}}{\biggr ]}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{n+2}+1}}}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48152e52c3eb9c14398e29907e759b53900153c6)
![{\displaystyle {\frac {1}{\sqrt {x^{4}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{2}}F{\biggl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c42e35cf46076ad7140865bd7327f051d0af90)

![{\displaystyle {\frac {1}{4{\sqrt {2}}}}\csc {\bigl (}{\frac {\pi }{4}}{\bigr )}\beta {\bigl (}{\frac {1}{4}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{4}+1}}}\,\mathrm {d} x={\biggl \{}{\color {blue}{\frac {1}{2}}F{\biggl [}2\arctan(x);{\frac {1}{2}}{\sqrt {2}}\,{\biggr ]}}{\biggr \}}_{x=0}^{x=\infty }=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce35084cada7d06712bd0cf775c1560f9a43ab7e)


![{\displaystyle {\frac {1}{\sqrt {x^{6}+1}}}={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{6}}{\sqrt[{4}]{27}}F{\biggl [}2\arctan {\biggl (}{\frac {{\sqrt[{4}]{3}}\,x}{\sqrt {x^{2}+1}}}{\biggr )};{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\biggr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3186259fdf61a7ebb632f3d02d679cae524c35f7)

![{\displaystyle {\frac {1}{6{\sqrt[{3}]{2}}}}\csc {\bigl (}{\frac {\pi }{6}}{\bigr )}\beta {\bigl (}{\frac {1}{3}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{6}+1}}}\,\mathrm {d} x={\biggl \{}{\color {blue}{\frac {1}{6}}{\sqrt[{4}]{27}}F{\biggl [}2\arctan {\biggl (}{\frac {{\sqrt[{4}]{3}}\,x}{\sqrt {x^{2}+1}}}{\biggr )};{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\biggr ]}}{\biggr \}}_{x=0}^{x=\infty }=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aeaa28cc9c443e551ccbc434cd63421302cae2b)
![{\displaystyle ={\frac {1}{6}}{\sqrt[{4}]{27}}F{\bigl [}2\arctan({\sqrt[{4}]{3}});{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\bigr ]}={\frac {2}{9}}{\sqrt[{4}]{27}}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}+{\sqrt {2}}){\bigr ]}={\frac {2}{3}}{\sqrt[{4}]{3}}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d55b9913617b5871c7a524c0eeec8168828a1c5a)
![{\displaystyle {\color {ForestGreen}K{\bigl [}{\frac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}={\frac {1}{2{\sqrt[{3}]{2}}{\sqrt[{4}]{3}}}}\beta {\bigl (}{\frac {1}{3}}{\bigr )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fffa258bf7309994a5d54ae0f95d4614975d1ec2)

![{\displaystyle ={\frac {\mathrm {d} }{\mathrm {d} x}}\,{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9418c896b8d195e1c5bce8b760e71d95bd9cf29e)

![{\displaystyle {\frac {1}{8{\sqrt[{4}]{2}}}}\csc {\bigl (}{\frac {\pi }{8}}{\bigr )}\beta {\bigl (}{\frac {3}{8}}{\bigr )}=\int _{0}^{\infty }{\frac {1}{\sqrt {x^{8}+1}}}\,\mathrm {d} x=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21e13acda89a6825a0a7a6477bf0e2d072b3ce9e)
![{\displaystyle ={\biggl \langle }{\color {blue}{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}2\arctan {\biggl [}{\frac {2\cos(\pi /8)\,x}{{\sqrt {x^{4}+{\sqrt {2}}\,x^{2}+1}}-x^{2}+1}}{\biggr ]};2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}+{\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\biggl \{}\arcsin {\biggl [}{\frac {2\cos(\pi /8)\,x}{x^{2}+1}}{\biggr ]};\tan {\bigl (}{\frac {\pi }{8}}{\bigr )}{\biggr \}}}{\biggr \rangle }_{x=0}^{x=\infty }=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ab622f4004af8bce9bb3de38a20ecb4d4219a21)
![{\displaystyle ={\frac {1}{4}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}F{\bigl [}\pi ;2{\sqrt[{4}]{2}}\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}{\bigr ]}={\frac {1}{2}}\sec {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2{\sqrt {2}}-2}}{\bigr )}=2\sin {\bigl (}{\frac {\pi }{8}}{\bigr )}K({\sqrt {2}}-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85a8ad3dc4c269cf0392b1260587f5471ae5e932)
![{\displaystyle {\color {ForestGreen}K({\sqrt {2}}-1)={\frac {1}{8}}{\sqrt[{4}]{2}}\,({\sqrt {2}}+1)\,\beta {\bigl (}{\frac {3}{8}}{\bigr )}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/177a0e98ca0233f21a20d37c9dd285369ecf1cda)

![{\displaystyle q[{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}})]=\exp(-{\sqrt {3}}\,\pi )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d8a66693d1cd78fa0422519e6a5f523cfa1f69)

![{\displaystyle \theta _{3}[\exp(-\pi )]=\theta _{3}[q({\tfrac {1}{2}}{\sqrt {2}})]={\sqrt {2\pi ^{-1}K({\tfrac {1}{2}}{\sqrt {2}})}}=2^{-1/2}\pi ^{-1/2}\beta ({\tfrac {1}{4}})^{1/2}=2^{-1/4}{\sqrt[{4}]{\pi }}\,{\Gamma {\bigl (}{\tfrac {3}{4}}{\bigr )}}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c3b3090803e98069d65099cffee88f085fb58b6)
![{\displaystyle \theta _{3}[\exp(-{\sqrt {3}}\,\pi )]=\theta _{3}{\bigl \{}q{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}{\bigr \}}={\sqrt {2\pi ^{-1}K{\bigl [}{\tfrac {1}{4}}({\sqrt {6}}-{\sqrt {2}}){\bigr ]}}}=2^{-1/6}3^{-1/8}\pi ^{-1/2}\beta ({\tfrac {1}{3}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2456d11eb2e069e9d2eac7d2cc91561418429672)
![{\displaystyle \theta _{3}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{3}[q({\sqrt {2}}-1)]={\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/8}\cos({\tfrac {1}{8}}\pi )\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81e6d7302b7c5a86bd706212afbf5c0dddc4be6d)
![{\displaystyle \theta _{4}[\exp(-{\sqrt {2}}\,\pi )]=\theta _{4}[q({\sqrt {2}}-1)]={\sqrt[{4}]{2{\sqrt {2}}-2}}\,{\sqrt {2\pi ^{-1}K({\sqrt {2}}-1)}}=2^{-1/4}\cos({\tfrac {1}{8}}\pi )^{1/2}\,\pi ^{-1/2}\beta ({\tfrac {3}{8}})^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07c0cdf2fb31e0ad42c1c55d8562d70da28f2203)




 다음 표에 나열됩니다.
다음 표에 나열됩니다.![{\displaystyle \sum _{k=0}^{\infty }P(k)x^{k}={\frac {1}{(x;x)_{\infty }}}=\theta _{3}(x)^{-1/6}\theta _{4}(x)^{-2/3}{\biggl [}{\frac {\theta _{3}(x)^{4}-\theta _{4}(x)^{4}}{16\,x}}{\biggr ]}^{-1/24}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d45936d0522b1f639420fa97f49e237424fa4a51)
![{\displaystyle (x;x)_{\infty }=1+\sum _{n=1}^{\infty }{\bigl [}-x^{{\text{Fn}}(2n-1)}-x^{{\text{Kr}}(2n-1)}+x^{{\text{Fn}}(2n)}+x^{{\text{Kr}}(2n)}{\bigr ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eab59cb2fcf2f3ddc6f1e10561a526de51f516f3)




![{\displaystyle \sum _{k=0}^{\infty }Q(k)x^{k}={\frac {1}{(x;x^{2})_{\infty }}}=\theta _{3}(x)^{1/6}\theta _{4}(x)^{-1/3}{\biggl [}{\frac {\theta _{3}(x)^{4}-\theta _{4}(x)^{4}}{16\,x}}{\biggr ]}^{1/24}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faf3d08f52a11ebbc9e5b9289d4f784f60f103d7)





 정규 파티션 시퀀스
정규 파티션 시퀀스
![{\displaystyle \theta _{4}(x)={\biggl [}\sum _{k=0}^{\infty }P(k)x^{k}{\biggr ]}^{-1}{\biggl [}\sum _{k=0}^{\infty }Q(k)x^{k}{\biggr ]}^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ed01dd893d339d67b7cffd351479d11bd83f819)


 동등하지 않습니다. 여기서
동등하지 않습니다. 여기서



