발생 구조
Incidence structure수학에서 발생 구조는 두 가지 유형의 물체와 이러한 유형의 물체 사이의 단일 관계로 구성된 추상적 체계다.유클리드 평면의 점 및 선을 두 가지 유형의 객체로 간주하고 모든 점 및 선에 대해 점들이 어떤 선에 있는지 관계를 제외하고 이 기하학의 모든 특성을 무시하십시오.남은 것은 유클리드 평면의 발생 구조다.
발생 구조는 흔히 평면(예: 아핀, 투영, 뫼비우스 평면)에서 추상화하여 일반화하는 기하학적 맥락에서 고려되지만, 개념은 매우 광범위하고 기하학적 설정에 국한되지 않는다.기하학적 설정에서도 발생 구조는 점이나 선에만 국한되지 않고 고차원 객체(플레인, 고체, n-스페이스, 원뿔 등)를 사용할 수 있다.유한 구조물에 대한 연구를 유한 기하학이라고도 한다.[1]
공식 정의 및 용어
발생 구조는 3중(P, L, I)이며, 여기서 P는 점이라고 하는 원소를 가진 집합이고, L은 선이라고 하는 요소를 가진 구별되는 집합이며, I ⊆ P × L은 발생 관계다.나의 원소는 깃발이라고 불린다.만약 (p, l)이 I에 있다면, 사람들은 점 p "거짓말" l 또는 점 l가 "통과" p라고 말할 수 있다.이 관계의 대칭적 성격을 반영하기 위해 더 많은 "대칭적" 용어는 "p는 l와 사건" 또는 "l은 p와 사건"이며, (p, l) ∈ I과 동의어인 p I라는 표기법을 사용한다.[2]
어떤 일반적인 상황에서 L은 P의 하위 집합일 수 있으며, 이 경우 나는 격납된다(p I l p가 l의 멤버인 경우에만).이러한 유형의 발병 구조를 set-theoretic이라고 한다.[3]예를 들어 P가 벡터 집합과 L의 제곱 행렬 집합인 경우 I = {(v, M)를 정의할 수 있다. 벡터 v는 행렬 M의 고유 벡터다. 이 예는 점과 선의 기하학적 언어를 사용하지만 객체 유형이 이러한 기하학적 객체가 될 필요는 없다는 것을 보여준다.
예
1. 파노 평면
3. 일반화 쿼드랭글
4. 뫼비우스-칸토르 구성
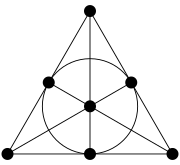
5. 파푸스 구성
각 라인이 동일한 수의 점으로 입사하는 경우 입사 구조는 균일하다.두 번째를 제외한 이 예들은 각각 한 줄에 3점씩 균일하다.
그래프
모든 그래프(단순할 필요는 없음, 루프와 다중 에지가 허용됨)는 라인당 두 점을 갖는 균일한 발생 구조다.이러한 예에서 그래프의 정점은 점 집합을 형성하고, 그래프의 가장자리는 선 집합을 형성하며, 발생률은 정점이 에지의 끝점임을 의미한다.
선형공간
발병 구조는 그 전체 일반성으로 연구되는 경우가 거의 없다. 추가 공리를 만족하는 발병 구조를 연구하는 것이 일반적이다.예를 들어, 부분 선형 공간은 다음을 만족하는 발생 구조다.
- 두 개의 구별되는 점은 공통선이 거의 하나일 때 발생하며,
- 한 줄 한 줄에 최소한 두 개의 점이 있다.
위의 첫 번째 공리가 더 강한 공리로 대체되는 경우:
- 어떤 두 개의 뚜렷한 점은 정확히 하나의 공통선을 가진 사건이다.
그물
좀 더 전문화된 예는 k-net이다.이것은 선들이 k 평행 등급으로 떨어져 같은 평행 등급의 두 선은 공통점이 없지만 서로 다른 등급의 두 선은 정확히 하나의 공통점을 가지며, 각 점은 각 평행 등급에서 정확히 하나의 선에 속하는 발생 구조다.k-net의 예는 아핀 평면의 점 집합과 아핀 선의 k 병렬 등급이다.
이중구조
만약 우리가 "포인트"와 "라인"의 역할을 교환한다면
- C = (P, L, I)
우리는 이중 구조를 얻는다.
- C∗ = (L, P, I∗),
여기서∗ 나는 나의 역관계다.이는 다음의 정의에서 즉시 따르게 된다.
- C∗∗ = C.
이중 C에∗ 대해 이형성이 있는 구조 C를 자기 이중이라고 한다.위의 파노 평면은 자가이중 발생 구조다.
기타 용어
발생 구조의 개념은 매우 단순하며 여러 분야에서 발생했는데, 각각은 고유의 어휘를 소개하고 이러한 구조에 대해 일반적으로 질문되는 질문의 유형을 명시한다.발생 구조는 기하학적 용어를 사용하지만 그래프 이론적 용어로는 하이퍼그래프, 설계 이론적 용어로는 블록 설계라고 불린다.그것들은 일반적인 맥락에서 집합 시스템 또는 집합 집합의 패밀리로도 알려져 있다.
하이퍼그래프

각각의 하이퍼그래프나 세트 시스템은 유니버설 세트가 "점"의 역할을 하고, 해당 세트의 패밀리가 "선"의 역할을 하며, 발생 관계가 "선"으로 설정된 멤버쉽을 갖는 발병 구조로 간주할 수 있다.반대로, 모든 발생 구조는 그것과 관련된 점들의 집합으로 선을 식별함으로써 하이퍼그래프로 볼 수 있다.
블록 설계
(일반) 블록 설계는 X의 부분 집합 F와 함께 집합 X이다(반복된 부분 집합 허용).일반적으로 수치 정규성 조건을 만족시키기 위해서는 블록 설계가 필요하다.입사 구조로서 X는 점 집합이고 F는 보통 이 맥락에서 블록이라고 하는 선 집합이다(반복된 블록은 별개의 이름을 가져야 하므로 F는 실제로 멀티셋이 아니라 집합이다).F의 모든 부분 집합이 동일한 크기를 갖는 경우 블록 설계를 균일하다고 한다.X의 각 요소가 동일한 수의 부분 집합에 나타나면 블록 설계는 정규적이라고 한다.획일적인 디자인의 이중은 규칙적인 디자인이고 그 반대의 경우도 마찬가지다.
예:파노 평면
블럭 설계/하이퍼그래프는 다음에서 제공하는 것을 고려하십시오.
- ={ 1,,,,,, 2,3,6,
- .
이 발병 구조를 파노 평면이라고 한다.블록 설계로서 그것은 균일하고 규칙적이다.
주어진 라벨링에서 선은 정확히 라벨이 0까지 추가된 점 3개로 구성된 점의 부분 집합이다.또는 2진수로 쓸 때 각 숫자는 2진수 필드 위에 길이 3의 0이 아닌 벡터로 식별할 수 있다.아공간을 생성하는 세 벡터는 선을 형성한다. 이 경우 벡터 합이 0 벡터인 것과 같다.
표현
발병 구조는 여러 가지 방법으로 나타낼 수 있다.집합 P와 L이 유한한 경우, 이러한 표현은 구조물에 관련된 모든 관련 정보를 압축적으로 인코딩할 수 있다.
발생 행렬
(마침표) 발생 구조의 발생 행렬은 (0,1) 행렬로, {pi} 지점에 의해 그 행이 색인화되고, pi I l과j 0이 아닌 경우 ij-th 항목이 1인 {lj} 선에 의해 색인화된다.[6]발생 행렬은 점 및 선의 임의 순서에 따라 달라지기 때문에 고유하게 결정되지 않는다.[7]
위에 그림(예: 숫자 2)과 같은 균일하지 않은 발생 구조는 다음과 같이 제시된다.
- P = {A, B, C, D, E, P}
- L = {l = {C, P, E}, m = {P}, n = {P, D}, o = {P, A}, p = {A, B}, q = {P, B} }.
이 구조물의 발생 행렬은 다음과 같다.
발생률 표에 해당하는 경우:
I l m n o p q A 0 0 0 1 1 0 B 0 0 0 0 1 1 C 1 0 0 0 0 0 D 0 0 1 0 0 0 E 1 0 0 0 0 0 P 1 1 1 1 0 1
발생 구조 C가 발생 행렬 M을 갖는 경우, 이중 구조 C는∗ 전치 행렬 M을T 발생 행렬로 가지고 있다(그리고 이 행렬로 정의된다).
발생 구조는 점 및 선의 순서가 존재하여 그 순서에 따라 구성된 발생 행렬이 대칭 행렬이 되도록 하는 경우 자가 이중이다.
위의 예 1번에서 주어진 라벨과 A, B, C, D, G, F, E, l, p, n, s, r, m, q를 순서에 따라 정렬된 선으로 파노 평면에 발생 행렬이 있다.
이것은 대칭 행렬이기 때문에 파노 평면은 자기 이중 발생 구조다.
화보 표현
발생 수치(즉, 발생 구조의 묘사)는 평면에서 점으로 점을 나타내며 선에 대응하도록 점들을 결합하는 시각적 수단을 갖는 것으로 구성된다.[7]점들은 어떤 방식으로든 배치될 수 있으며, 점들 사이의 거리나 점들 간의 관계에 제한이 없다.발생 구조에서 한 점이 다른 두 점 사이에 있다는 개념은 없다. 선상의 점 순서는 정의되지 않는다.이것을 중간이라는 개념이 있는 순서형 기하학과 비교해 보라.선들의 묘사에 대해서도 같은 진술을 할 수 있다.특히, 선은 "직선 세그먼트"로 묘사될 필요가 없다(위의 예 1, 3, 4 참조).그래프의 그림적 표현과 마찬가지로, 점 이외의 어떤 장소에서 두 개의 "선"을 교차하는 것은 발생 구조 면에서 의미가 없으며, 단지 표현상의 우연일 뿐이다.이러한 발생 수치는 때때로 그래프를 닮을 수 있지만, 발생 구조가 그래프가 아니면 그래프가 아니다.
실현 가능성
발생 구조는 발생의 일반적인 기하학적 의미를 갖는 유클리드 평면의 점과 곡선으로 모델링할 수 있다.일부 발생 구조는 점 및 (직선) 선에 의한 표현을 허용한다.할 수 있는 구조는 실현 가능하다고 불린다.주변 공간이 언급되지 않은 경우 유클리드 평면을 가정한다.Fano 평면(위의 1 예)은 적어도 하나의 곡선이 필요하기 때문에 실현이 불가능하다.뫼비우스-칸토르 구성(위 예 4)은 유클리드 평면에서 실현 가능하지 않지만, 복잡한 평면에서 실현 가능하다.[8]반면에 위의 사례 2와 5는 실현가능하며 거기서 주어진 발생 수치는 이를 증명한다.슈타인리츠(1894)[9]는 n-구성3(n 포인트와 n 라인이 있는 인시브 구조, 한 라인당 3 포인트, 각 포인트를 통과하는 3개의 라인)이 실현 가능하거나 그 표현에서 하나의 곡선만 사용해야 한다는 것을 보여주었다.[10]파노 평면은 고유(73)이고 뫼비우스-칸토르 구성은 고유(83)이다.
발생 그래프(Levi 그래프)

각 발생 구조 C는 구조물의 Levi 그래프 또는 발생 그래프로 불리는 초당적 그래프에 해당한다.모든 초당적 그래프는 두 가지 색상이 가능하기 때문에, 리바이스 그래프에는 흑백 정점 색상이 주어질 수 있는데, 여기서 검은 정점은 포인트에 해당하고 흰색 정점은 C의 선에 해당한다.이 그래프의 가장자리는 발생 구조의 플래그(사건 지점/선 쌍)에 해당한다.원래의 Levi 그래프는 순서 2의 일반화된 쿼드랭글의 발생률 그래프였지만([11]위 예 3) 모든 발생 구조의 발생률 그래프를 참조하기 위해 H.S.M. Coxeter에[12] 의해 항이 확장되었다.[13]
Levi 그래프 예제
Fano 비행기의 Levi 그래프는 Heawood 그래프다.히우드 그래프는 연결되고 정점 변환이 되기 때문에, 흑점과 백의 정점을 바꾸는 자동형성(히우드 그래프의 그림에서 수직축에 대한 반사로 정의되는 것과 같은)이 존재한다.이는 결국 파노 평면이 스스로 이중화됨을 암시한다.
뫼비우스-칸토르 구성의 레위 그래프(위 예 4)의 왼쪽에서 구체적인 표현은 //4의 중심(시계 방향 또는 시계 반대 방향)을 중심으로 회전하는 것이 파란 정점과 빨간 정점을 교차시키고 가장자리를 가장자리에 매핑하는 것을 보여준다.즉, 이 그래프의 색을 바꾸는 자동형이 존재한다는 것이다.따라서 뫼비우스-칸토르 구성으로 알려진 발병 구조는 자가이중이다.
일반화
두 가지 이상의 물체를 포함하도록 발생 구조의 개념을 일반화할 수 있다.k 종류의 물체를 가진 구조는 k등급이나 k등급 기하학의 발생 구조라고 불린다.[13]형식적으로 이것들은 Pi pj P = ∅과 함께 k + 1 튜플 S = (P1, P2, ..., Pk, I)로 정의된다.
이러한 구조물에 대한 Levi 그래프는 각 유형에 해당하는 정점이 동일한 다중 사이트 그래프로 정의된다.
참고 항목
메모들
- ^ 콜번 & 디니츠 2007, 페이지 702
- ^ a b 뎀보스키 1968, 페이지 1-2
- ^ 빌리오티, Jha & Johnson 2001, 페이지 508
- ^ 선형공간이라는 용어는 벡터공간을 가리키는 말로도 쓰이지만, 이것은 혼동을 일으키는 일은 거의 없을 것이다.
- ^ 무어하우스 2007, 페이지 5
- ^ 행을 선으로, 열을 점으로 지수화하는 다른 관습도 널리 사용된다.
- ^ a b Beth, Jungnickel & Lenz 1986, 페이지 17
- ^ 피산스키 & 세르바티우스 2013, 페이지 222
- ^ E. Steinitz (1894년), Uber die Construction der Configurationenn3, Statement, Breslau
- ^ Gropp, Harald (1997), "Configurations and their realizations", Discrete Mathematics, 174: 137–151, doi:10.1016/s0012-365x(96)00327-5
- ^ Levi, F. W. (1942), Finite Geometrical Systems, Calcutta: University of Calcutta, MR 0006834
- ^ Coxeter, H.S.M. (1950), "Self-dual configurations and regular graphs", Bulletin of the American Mathematical Society, 56: 413–455, doi:10.1090/s0002-9904-1950-09407-5
- ^ a b 피산스키 & 세르바티우스 2013 페이지 158
참조
- Beth, Thomas; Jungnickel, Dieter; Lenz, Hanfried (1986), Design Theory, Cambridge University Press, ISBN 3-411-01675-2
- Biliotti, Mauro; Jha, Vikram; Johnson, Norman L. (2001), Foundations of Translation Planes, Marcel Dekker, ISBN 0-8247-0609-9
- Colbourn, Charles J.; Dinitz, Jeffrey H. (2007), Handbook of Combinatorial Designs (2nd ed.), Boca Raton: Chapman & Hall/ CRC, ISBN 1-58488-506-8
- Dembowski, Peter (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, MR 0233275
- G. Eric Moorhouse (2014) 캘리포니아 대학교 리버사이드에서 존 배즈를 통한 입사 기하학
- Pisanski, Tomaž; Servatius, Brigitte (2013), Configurations from a Graphical Viewpoint, Springer, doi:10.1007/978-0-8176-8364-1, ISBN 978-0-8176-8363-4
추가 읽기
- CRC 프레스(2000).이산 및 조합 수학 지침서, (12.2장), ISBN 0-8493-0149-1
- 해럴드 L.도르와트 (1966) 발생 기하학, 프렌티스 홀