확장성이 없는 네트워크

시리즈의 일부
네트워크 과학
이론.
그래프 복잡한 네트워크 전염병 작은 세상 스케일프리 커뮤니티 구조 퍼콜레이션 진화 제어성 그래프 그리기 사회자본 링크 분석 최적화 상호주의 클로즈 호모필리 이동성 우선 첨부 균형 이론 네트워크 효과 사회적 영향
네트워크 타입
정보(컴퓨팅) 전기 통신 운송 사회의 과학적 협업 생물학적 인공 신경 상호의존적 의미론 공간의 의존 흐름 온칩
그래프
특징들 클리크 요소 인하. 사이클 data 구조 엣지 고리 근린 경로. 꼭지점 인접 리스트/매트릭스 발생 목록/매트릭스 종류들 초당파 완성하다 연출된 들뜬 멀티 랜덤 가중치
측정 기준 알고리즘
중앙집중성 도 모티브 클러스터링 학위 분포 구색성 거리 모듈러성 효율성.
모델
토폴로지 랜덤 그래프 에르데스-레니 바라바시-알베르트 비앙코니바라바시 피트니스 모델 와츠 스트로게츠 지수 랜덤(ERGM) 랜덤 지오메트릭(RGG) 쌍곡선(HGN) 계층적 확률 블록 블록 모델링 최대 엔트로피 소프트 컨피규레이션 LFR 벤치마크 다이내믹스 부울 네트워크 에이전트 베이스 전염병/S적외선
리스트 분류
토픽 소프트웨어 네트워크 과학자 카테고리:네트워크 이론 카테고리:그래프 이론
v t

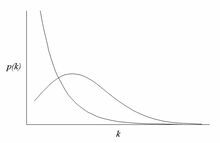
스케일 프리 네트워크는 적어도 점근적으로 멱함수의 법칙을 따르는 정도 분포를 가진 네트워크입니다.즉, 다른 노드에 k개의 접속을 가진 네트워크 내 노드의 비율 P(k)는 다음과 같이 k의 큰 값에 대해 사용됩니다.

${\displaystyle P(k)\sim \k^{\boldsymbol {-\gamma }}$

그 값은 대개 범위 2개체에는 어디에 있γ{\displaystyle \gamma}매개 변수, γ<>k− γ{\displaystyle k^{\boldsymbol{-\gamma}의 3{2<, \gamma<3\textstyle}(그 점에 두번째 순간(척도 모수)}} 하지만 그 최초의 순간)은 유한하지만, 이것은 가끔 이러한 김혜진입니다. 밖에서 거짓말할 수 있다고 무한하다ounds.[1][2]

통계 분석은 이러한 주장의 많은 부분을 반박하고 다른 ^[3][4]주장에도 심각하게 의문을 제기하고 있지만, 많은 네트워크는 스케일이 없는 것으로 보고되고 있습니다.또, 일부에서는, 통계적으로 엄격한 ^[5][6]정의에 따라 네트워크가 스케일 프리인지 아닌지를 아는 것보다, 단순히 학위 분포가 팻테일임을 아는 것이 더 중요하다고 주장해 왔습니다.우선 애착과 적합성 모델은 실제 네트워크에서 추측된 멱함수 법칙도 분포를 설명하기 위한 메커니즘으로 제안되었다.초선형 우선 접속이나 제2 네이버 우선 접속 등의 대체 모델은 일시적인 스케일 프리 네트워크를 생성하는 것처럼 보일 수 있지만 네트워크가 매우 ^[7][8]커짐에 따라 정도 분포는 멱함수 법칙에서 벗어납니다.

역사

Derek de Solla Price는 1965년 과학 논문 간의 인용 네트워크에 대한 연구에서 논문 링크의 수(즉, 받는 인용의 수)가 파레토 분포 또는 멱함수 법칙에 따라 두꺼운 꼬리를 가진 분포를 가지고 있으며, 따라서 인용 네트워크는 스케일 프리라는 것을 보여주었다.그러나 그는 수십 년이 지나서야 생겨난 "스케일 프리 네트워크"라는 용어를 사용하지 않았다.1976년 이후 논문에서 Price는 인용 네트워크에서 멱법칙의 발생을 설명하기 위한 메커니즘을 제안하기도 했습니다. 그는 이를 "누적적 이점"이라고 불렀지만 오늘날에는 선호 첨부라는 이름으로 더 일반적으로 알려져 있습니다.

scale-free 네트워크의 최근 관심 1999년에서 일하게 알버트 라즐로 바라바 시 및 동료에 의해 노트르담 대학교의 월드 와이드 Web,[9]의 일부를 그들이"허브"로 불리는 일부 노드이며, 한 전체적으로, 네트워크는 바로 멱함수 분포를 가진 다른 사람들보다 더 많은 연관이 있다는 토폴로지를 지도로 만들었다에 시작했다.의노드에 접속되어 있는 링크의 수.일부 소셜 네트워크와 생물학적 네트워크를 포함한 몇몇 다른 네트워크에도 굵은 꼬리 학위 분포가 있다는 것을 알게 된 후, Barabashi와 공동 연구진은 멱함수 법칙 학위 분포를 나타내는 네트워크의 클래스를 설명하기 위해 "스케일 프리 네트워크"라는 용어를 만들었습니다.그러나 Amaral 등은 사회, 경제, 기술, 생물 및 물리적 시스템에서 네트워크의 7가지 예를 연구한 결과, 이 7가지 사례 중에서 스케일 프리 네트워크를 찾을 수 없었다.이러한 예들 중 하나인 영화-배우 네트워크만이 중간 정도의 k에 대한 멱함수 법칙 체계에 따른 정도 분포 P(k)를 가졌다. 그러나 결국 이 멱함수 법칙 체계에는 큰 ^[10]k에 대한 지수적 붕괴를 보여주는 급격한 컷오프가 뒤따랐다.

바라바시와 레카 알베르트는 멱함수 분포의 외관을 설명하기 위한 생성 메커니즘을 제안했다. 이들은 이를 "우선적 애착"이라고 불렀으며 이는 본질적으로 Price가 제안한 것과 동일하다.이 메커니즘에 대한 해석적 해법(프라이스의 해법과 유사함)은 2000년에 도로고브체프, 멘데스, 사무킨에^[11] 의해 발표되었고 크라피브스키, 레드너, 레이브라즈에 의해 독립적으로 발표되었으며, 후에 수학자 벨라 볼로바스에 ^[12]의해 엄격하게 증명되었다.단, 특히 이 메커니즘은 스케일프리 클래스의 특정 네트워크 서브셋만 생성하며,^[13] 그 이후 많은 대체 메커니즘이 발견되었습니다.

스케일 프리 네트워크의 역사에는 약간의 의견 차이도 포함되어 있습니다.경험적 차원에서 여러 네트워크의 스케일프리 성격에 의문이 제기되었습니다.예를 들어 3형제 Faloutsos는 traceroute 데이터에 근거해 인터넷이 멱함수 법칙의 분포를 가지고 있다고 믿었습니다.다만, 이것은 라우터가 상호 접속하는 AS의 내부 레이어2 구조를 숨기면서 고도의 노드로 보이는 레이어3의 착시라고 생각되고 있습니다.^[14]

이론적인 차원에서 스케일 프리(scale-free)의 추상적 정의에 대한 개선이 제안되었다.예를 들어 Li 등.(2005)는 최근 보다 정확한 "스케일 프리 메트릭"을 제공하였다.간단히 말해, G는 엣지 집합E의 그래프이며, 도($deg)$에 ${\displaystyle \mathrm{의한}}$ $꼭지점{\displaystyle }$v$({displaystyle$ v$\},$ 즉 v {displaystyle $\deg(v$

$\displaystyle s(G)=\sum _{(u,v)\in E}\deg(u)\cdot \sum(v)}$

이는 고차 노드가 다른 고차 노드에 연결되어 있을 때 최대화됩니다.정의하다

${\displaystyle S(G)=frac {s(G)}{s_{\max}}}}$

여기서_max s는 G와 동일한 정도 분포를 가진 모든 그래프 세트에서 H에 대한 s(H)의 최대값이다.이는 0과 1 사이의 메트릭을 제공하며, 여기서 S(G)가 작은 그래프 G는 "척도가 높은" 그래프 G는 "척도가 없는" 그래프이다.이 정의는 "스케일 프리"라는 이름에 내포된 자기 유사성의 개념을 포착합니다.

개요

복잡한 네트워크에서의 스케일프리 속성의 출현을 설명하는 2개의 주요 컴포넌트가 있습니다.그것은 성장과 우선 ^[15]애착입니다.'성장'이란 장기간에 걸쳐 새로운 노드가 이미 존재하는 시스템인 네트워크에 결합하는 성장 과정을 의미합니다(10년간 수십억 개의 웹 페이지가 성장한 월드 와이드 웹과 같은).마지막으로 "우선 연결"이란 새로운 노드가 다른 노드와의 링크 수가 이미 많은 노드에 연결하는 것을 선호한다는 것을 의미합니다.따라서 더 많은 노드가 이미 많은 링크가 있는 노드에 링크되어 이 노드가 허브가 ^[9]될 가능성이 높아집니다.네트워크에 따라서는, 허브는 어소시에이션 또는 어소시에이션 해제 중 하나입니다.잘 연결된/유명한 사람들이 서로를 더 잘 아는 경향이 있는 소셜 네트워크에서 분류성을 찾을 수 있습니다.불협화음은 기술 네트워크(인터넷, 월드 와이드 웹)와 생물학적 네트워크(단백질 상호작용, ^[15]대사)에서 발견됩니다.

특성.

스케일 프리 네트워크에서 가장 주목할 만한 특징은 평균을 크게 초과하는 정도를 가진 정점의 상대적인 공통성이다.최상위 노드는 종종 "허브"라고 불리며, 이는 도메인에 따라 크게 달라지지만 네트워크에서 특정 목적을 수행하는 것으로 간주됩니다.

클러스터링

스케일 프리 네트워크의 또 다른 중요한 특징은 노드 정도가 증가함에 따라 감소하는 클러스터링 계수 분포입니다.이 분포는 또한 멱함수의 법칙을 따릅니다.즉, 저도의 노드는 매우 고밀도 서브그래프에 속하며 이러한 서브그래프는 허브를 통해 서로 연결되어 있습니다.노드가 사람이고 링크가 사람 간의 지인 관계인 소셜 네트워크를 생각해 보십시오.사람들이 커뮤니티를 형성하는 경향이 있다는 것을 쉽게 알 수 있다. 즉, 모두가 알고 있는 작은 그룹(이러한 커뮤니티는 완전한 그래프라고 생각할 수 있다).게다가, 커뮤니티의 구성원들은 그 커뮤니티 밖에 있는 사람들과도 몇 가지 친분을 맺습니다.그러나 일부 사람들은 많은 커뮤니티(예: 연예인, 정치인)와 연결되어 있다.그 사람들은 작은 세계 현상에 책임이 있는 허브로 여겨질지도 모른다.

현재 스케일 프리 네트워크의 보다 구체적인 특성은 네트워크의 작성에 사용되는 생성 메커니즘에 따라 달라집니다.예를 들어 우선 접속에 의해 생성된 네트워크는 일반적으로 네트워크 중앙에 높은 정점을 배치하여 서로 연결하여 코어를 형성합니다.코어와 주변부 사이의 영역은 점차적으로 낮은 수준의 노드가 구성합니다.정점의 대부분을 랜덤하게 삭제해도 네트워크 전체의 접속성에 거의 영향을 주지 않기 때문에 이러한 토폴로지가 보안에 도움이 될 수 있음을 알 수 있습니다.또한 타깃 공격은 접속성을 매우 빠르게 파괴합니다.주변부에 높은 정점을 배치하는 다른 스케일프리 네트워크에서는 이러한 특성이 나타나지 않습니다.마찬가지로 스케일 프리 네트워크의 클러스터링 계수는 다른 토폴로지의 상세 내용에 따라 크게 다를 수 있습니다.

예방접종

인터넷이나 소셜 네트워크와 같은 현실적인 네트워크를 대표하는 자유 네트워크를 효율적으로 면역화하는 방법에 대한 문제는 광범위하게 연구되어 왔다.이러한 전략 중 하나는 가장 큰 수준의 노드(예: 의도적인 공격)를 면역화하는 것입니다. 이 경우 ${\displaystyle }$ c$$c c { $displaystyle$ c$$}는$$ 상대적으로 높고 면역에 필요한 노드 수가 적기 때문입니다.그러나 많은 현실적인 경우 글로벌 구조를 사용할 수 없으며 가장 큰 수준의 노드를 알 수 없습니다.

그래프 변환에서 랜덤 그래프의 속성은 변경되거나 변경되지 않을 수 있습니다.예를 들어, Mashaghi A. 등은 랜덤 그래프를 에지-이중 그래프(또는 선 그래프)로 변환하는 변환이 거의 동일한 정도 분포의 그래프 앙상블을 생성하지만 정도 상관과 상당히 높은 클러스터링 계수를 갖는 그래프를 생성한다는 것을 입증했다.따라서 스케일 프리 그래프는 이러한 변환 ^[16]하에서도 스케일 프리 상태로 유지됩니다.

예

많은 실제 네트워크는 확장성이 없다고 생각되지만, 그 근거는 주로 보다 엄격한 데이터 분석 ^[3]기술에 대한 인식이 발달하고 있기 때문에 종종 결론을 내리지 못하고 있습니다.이와 같이, 많은 네트워크의 규모 없는 성격은 과학계에서 여전히 논의되고 있다.스케일 프리라고 생각되는 네트워크의 예를 다음에 나타냅니다.

• 콜라보레이션 네트워크를 포함한 일부 소셜 네트워크.광범위하게 연구된 두 가지 예는 영화 속 영화배우들의 협업과 논문 수학자들의 공동저작이다.
• 인터넷과 월드 와이드 웹의 웹그래프를 포함한 많은 종류의 컴퓨터 네트워크.
• 소프트웨어 종속성 그래프.^[17] 그 중 일부는 생성 ^[18]모델로 설명됩니다.
• 은행간 결제 네트워크 등 일부 금융 네트워크
• 단백질-단백질 상호작용 네트워크.
• 시멘틱 ^[21]네트워크
• 항공사 네트워크

저울이 ^[22]없는 위상은 고온 초전도체에서도 발견되었다.고온 초전도체의 품질 - 전자가 양자 물리 법칙을 따르고 마찰 없이 완벽하게 동기하여 흐르는 화합물 - 은 겉으로 보기에 무작위 산소 원자의 프랙탈 배열과 격자 ^[23]왜곡과 관련이 있는 것으로 보입니다.

공간 채우기 셀 구조인 가중 평면 확률 격자(WPSL)는 최근 좌표 번호 분포가 멱법칙을 따르는 것이 제안되었다.이것은 격자가 몇 개의 블록을 가지고 있다는 것을 의미하며, 그 블록들은 놀라울 정도로 많은 이웃들을 가지고 있으며, 그들은 공통의 경계를 공유하고 있다.시공은 개시자(예를 들어 단위 면적의 정사각형)와 이를 무작위로 4개의 블록으로 나누는 발전기로 시작합니다.이후 발전기는 해당 영역에 대해 우선적으로 선택된 사용 가능한 블록 중 하나에 대해 순차적으로 반복적으로 적용된다.그 결과 정사각형이 서로 배타적인 작은 직사각형 블록으로 분할됩니다.WPSL(DWPSL)의 듀얼은 각 블록을 노드를 중심으로 치환하고 대응하는 2개의 정점을 연결하는 엣지를 가진 블록 간의 각 공통 경계선을 멱함수 ^[24][25]법칙에 따라 도분포가 이루어지는 네트워크로 나타납니다.그 이유는 특혜적 압류 규칙을 구현하면서도 위장적으로 조정 주도의 압류 모델 규칙에 따라 성장하기 때문이다.

생성 모델

스케일 프리 네트워크는 우연만으로 발생하는 것이 아닙니다.Erd rés와 Rényi(1960)는 각 단계에서 두 개의 노드가 무작위로 균일하게 선택되고 그 사이에 링크가 삽입되는 그래프에 대한 성장 모델을 연구했다.이러한 랜덤 그래프의 속성은 스케일 프리 네트워크에서 볼 수 있는 속성과는 다르므로 이 성장 프로세스의 모델이 필요합니다.

스케일 프리 네트워크의 서브셋에 대해 가장 널리 알려진 생성 모델은 Barabasi와 Albert(1999)의 리치 생성 모델입니다.이 모델에서는 새로운 웹 페이지마다 기존 웹 페이지에 대한 링크가 생성되며, 이 링크는 균일하지 않지만 현재의 웹 페이지 수준에 비례합니다.이 모델은 1965년 Derek J. de Solla Price에 의해 누적 우위성이라는 용어로 발명되었지만, Barabashi가 현재 이름(BA 모델)으로 결과를 재발견할 때까지 인기를 끌지 못했다.이 프로세스에 따르면, 많은 인링크가 있는 페이지는 일반 페이지보다 더 많은 인링크를 끌어들인다.이로 인해 멱함수의 법칙이 생성되지만 결과 그래프는 밀접하게 연결된 작은 커뮤니티의 존재 등 다른 속성에서 실제 웹 그래프와 다릅니다.보다 일반적인 모델과 네트워크 특성이 제안되고 연구되고 있습니다.예를 들어, Pachon et al. (2018)는 두 가지 다른 부가 규칙, 즉 우선 부가 메커니즘과 가장 최근의 ^[26]노드에 대해서만 균일한 선택을 고려하는 리치 앤 리치 생성 모델의 변형을 제안했다.리뷰는 도로고브체프와 멘데스의 책을 ^{[citation needed]}참조한다.초선형 우선 접속이나 제2의 인접 접속등의 메카니즘은, 일시적으로 스케일 프리인 네트워크를 생성하지만, 네트워크의 ^[7][8]확대에 수반해 멱함수 법칙으로부터 벗어납니다.

Pennock 등에 의해 웹 링크에 대한 다소 다른 생성 모델이 제안되었다.(2002).그들은 대학, 공기업, 신문, 과학자와 같은 특정 주제에 관심이 있는 커뮤니티를 조사하여 웹의 주요 거점을 폐기하였다.이 경우 링크의 분포는 더 이상 멱함수의 법칙이 아니라 정규 분포와 비슷합니다.이러한 관찰에 기초하여, 저자들은 선호 애착을 연결점을 얻을 수 있는 기준 확률과 혼합하는 생성 모델을 제안했다.

또 다른 생성 모델은 Kumar ^[27]등이 연구한 복사 모델이다.(2000), 새로운 노드가 무작위로 기존 노드를 선택하고 기존 노드의 링크 일부를 복사합니다.이는 또한 멱함수의 법칙을 생성합니다.

네트워크의 증가(새로운 노드 추가)는 스케일프리 네트워크를 구축하기 위해 필요한 조건은 아닙니다.한 가지 가능성(Caldarelli 등 2002)은 구조물을 정적인 것으로 간주하고 관련된 두 정점의 특정 특성에 따라 정점 사이의 연결을 그리는 것이다.이러한 정점 속성(적합도)에 대한 통계적 분포를 지정하면 정적 네트워크에서도 스케일 프리 속성이 개발되는 것으로 판명됩니다.

일반화된 스케일 프리 모델

스케일 프리 복합 네트워크의 모델링에 있어서의 활동이 급증하고 있습니다.바라바시와^[28] 알베르트의 레시피는 몇 가지 변형과 일반화^{[29][30][31][32][26]} 그리고 이전의 수학 ^[33]작품들의 개조에 따라왔다.모델에 멱함수의 법칙 분포가 존재하는 한 이 네트워크는 스케일이 필요 없는 네트워크이며, 그 네트워크의 모델은 스케일이 필요 없는 모델입니다.

특징들

많은 실제 네트워크는 (대략) 스케일이 필요 없기 때문에 이를 설명하기 위해서는 스케일이 필요 없는 모델이 필요합니다.Price의 계획에서는 스케일 프리 모델을 구축하기 위해 다음 두 가지 요소가 필요합니다.

1. 노드 추가 또는 삭제통상, 네트워크 확장, 즉 노드 추가에 주력하고 있습니다.

2. 우선 첨부:새로운 노드가 "오래된" 노드에 연결될 확률$\delta$(\$displaystyle\Pi).$

일부 모델(아래의 Dangalchev^[34] 및 Fitness 모델 참조)은 노드 수를 변경하지 않고 정적으로 작동할 수 있습니다.또, 「우선 애착」모델이 스케일 프리 네트워크를 낳는다고 해서, 이것이 스케일 프리 네트워크의 진화의 기초가 되는 메카니즘이라는 것을 증명하는 것은 아닙니다.실제 시스템에서는 스케일 프리 네트워크에는 다른 메카니즘이 존재해, 스케일링이 발생할 가능성이 있기 때문입니다.

예

스케일 프리 네트워크 속성을 생성하려는 시도가 여러 번 있었습니다.다음은 몇 가지 예입니다.

바라바시-알베르트 모델

Price 모델의 무방향 버전인 Barabasi-Albert 모델은 선형 우선 부가${\displaystyle }\delta {\displaystyle \mathrm{}}$ (${\displaystyle k_{}}$i ) ${\displaystyle =}$ ${\displaystyle \frac{k_{}}{}}$ ${\displaystyle \frac{\underset{}{i}}{}}$ ${\displaystyle \frac{{}_{}}{\underset{}{}}}$ ${\displaystyle \frac{j_{}}{}}$j {$display$ \$Pi$ ( k$_$ { i ) =$frac${ $k$_ { $i$}}{\$sum$_ {$j}k_{j$}}}}를$$ 가지며, 단계마다 하나의 새로운 노드를 추가합니다.

(실제 네트워크에서의${\displaystyle }\pi {\displaystyle \mathrm{}}$ (${\displaystyle k}$) \ $displaystyle \ Pi$ ($k$ )의$$ 또 다른 일반적인 특징은 $\pi {\displaystyle \mathrm{}}$ ${\displaystyle (0}$ )${\displaystyle }$0$$0 ${\displaystyle 0}$ 00 { $displaystyle \ Pi$ ($0$ )\ $neq$0$$입니다.즉, 새로운 노드가 격리된 노드에 접속될 가능성은 제로 이외입니다.따라서$$ 일반적으로${\displaystyle }$$\pi {\displaystyle \mathrm{}}$ (${\displaystyle k}$) { $displaystyle \ Pi$ ($$${\displaystyle k}$) ${\displaystyle =A}$ + ${\displaystyle k^{}}$α { $displaystyle \ Pi$ ( k ) $=$$A+k^{\alpha$ $여기$서 A$(\displaystyle$ A$)$는 노드의 초기 매력입니다.)

2레벨 네트워크 모델

Dangalchev([43] 참조)는 우선 부착에서 대상 노드의 인접 노드 각각의 중요성을 고려하여 2-L 모델을 구축한다.2-L 모델에서 노드의 매력은 노드에 링크된 노드의 수뿐만 아니라 각 노드의 링크 수에 따라 달라집니다.

${\displaystyle \Pi (k_{i})=paramfrac {k_{i}+C\sum _{j}{{j}}{\sum _{j}k_{j}+C\sum _{j}{2}}$

여기서 C는 0과 1 사이의 계수입니다.

2-L 모델의 변형인 k2 모델은 첫 번째와 두 번째 인접 노드가 대상 노드의 매력에 동등하게 기여하는 것으로, 일시적인 스케일 프리 네트워크의 ^[8]출현을 보여줍니다.k2 모델에서는 네트워크가 비교적 작은 한 정도 분포는 대략적으로 스케일 프리인 것처럼 보이지만 네트워크가 커짐에 따라 스케일 프리 체제로부터의 현저한 편차가 나타납니다.따라서 시간이 지남에 따라 변화하는 정도의 노드의 상대적 매력이 나타나며 실제 네트워크에서도 볼 수 있는 기능입니다.

중개 주도형 접속(MDA) 모델)

MDA(Mediation-Drived Attachment) 모델에서는 m개의$${\$displaystyle$ m$}$개의$$$$ 엣지를 $가진{\displaystyle }$ 새로운 노드가 기존의 접속 노드를 랜덤으로 선택한 후 그 노드가 아닌$m개$의 인접 노드와의 $접속$을 실시합니다.기존 노드의 $노드{\displaystyle }$i(\$displaystyle$i)가$$ 선택되었을 확률 $)\displaystyle\Pi(i)$는 다음과 같습니다.

${\displaystyle\Pi(i)=paramfrac{k_{i}}{\frac{sum_{j=1}^{k_{i}}{\frac{k_{i}}}}{k_{i}}}}}.}$

계수${\displaystyle \frac{\underset{\mathrm{extensive}}{\overset{}{}}}{}}$ j ${\displaystyle \frac{\underset{}{\overset{}{=}}}{}}$ ${\displaystyle \frac{\underset{}{\overset{}{{}_{}}}}{}}$ k ${\displaystyle \frac{\underset{}{\overset{}{i_{}}}}{}}$ ${\displaystyle \frac{\frac{{}_{}}{}}{}}$ ${\displaystyle \frac{\frac{k_{}}{}}{}}$ j$$ { $displaystyle${ $frac _${ j$$= 1 }^{ $k$_ { $i$} } } { \ $frac {1$} { k _ { j }} } extensive 、 k$_$ { i$$}} extensive$$ 、 ${\displaystyle k_{}}$_ $display$ $style$ k $_ i$$$extensive$$ $extensive$ $extensive{\displaystyle }$ extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive extensive 。Ym> 큰 N{N\displaystyle}한도에서 14{\displaystyle m>, 14}평균 IHM 값이 상수는 뜻 Π(나는)∝ k나는{\displaystyle \Pi(나는)\propto k_{나는}}. 그것은 내포하고 있는 것이 높은 링크(학위) 노드가 더 높은 그 기회를 얻고 더 많은 유대부터 되어에 도달에 더 큰 numbe.w의 rays는 본질적으로 풍부하고 풍부한 메커니즘(또는 Barabasi의 우선 애착 규칙)의 직관적인 아이디어를 구체화하는 중재자를 통해 이루어진다.Albert 모델).따라서 MDA 네트워크는 PA 규칙을 따르고 있지만 ^[35]위장되어 있는 것으로 보입니다.

그러나 m ${\displaystyle =}$ {$displaystyle$ m$=1}$의 경우 전체 노드 ${\displaystyle \mathrm{중}}$ 거의 $99$가 1등급이고 1등급이 매우 높은 것으로 나타났기 때문에 승자가 모든 메커니즘을 취한다는 것을 설명합니다.$($디스플레이 $스타일$ m$)$ 값이$$ 슈퍼 빈부격차를 줄이고, m$디스플레이 스타일 m)$ 값이 보다 부익부 빈익빈 메커니즘으로 이행하고 있음을 알 수 있습니다.

비선형 우선 부착

Barabasi-Albert 모델에서는 노드가 $노드{\displaystyle }$i(\$displaystyle$$$i$)$에 접속할 $(k)$가 $노드$ i(\$displaystyle$ i$)$의 k$(\displaystyle$ k$)$에 비례한다고 가정합니다.This assumption involves two hypotheses: first, that ${\displaystyle \Pi (k)}$ depends on ${\displaystyle k}$, in contrast to random graphs in which ${\displaystyle \Pi (k)=p}$, and second, that the functional form of ${\displaystyle \Pi (k)}$ is linear in ${\displaystyle k}$.

비선형 우선부착에서는$δ$k$)\$displaystyle$\Pi(k)$의 형태가 선형이 아니며, 최근 연구에서 정도분포가 함수${\displaystyle }\delta {\displaystyle \mathrm{}}$($)\displaystyle\Pi(k)$의 형상에 따라 크게 좌우된다는 것이 밝혀졌다.

Krapivsky, Redner 및 Leyvraz는^[31] 비선형 우선 접속을 위해 네트워크의 스케일프리 특성이 파괴됨을 보여줍니다.네트워크의 topology가 스케일 프리인 유일한 경우는 우선 접속이 점근적으로 선형인 경우입니다.$즉{\displaystyle \mathrm{},}$ 우선 접속이 ki$($)~$(k_{i})\sim a_{\infty }k_{i}$입니다$(ki→\displaystyle k_{i$

${\displaystyle P(k)\sim k^{-\infty}{\text{ with }}}\text{\text{\frac {\frac {mu}}{a_{\infty }}}}.}$

이렇게 하면 도 분포의 지수를 2 ~ $（$ \ $displaystyle$\ $infty$ $\}$^{[clarification needed]} ）의 임의의 값으로 조정할 수 있습니다.

계층형 네트워크 모델

계층형 네트워크 모델은 설계상 확장성이 없으며 ^[36]노드의 클러스터링이 높습니다.

반복적인 구성은 계층적 네트워크로 이어집니다.5개의 노드로 구성된 완전히 연결된 클러스터에서 시작하여 각 클러스터의 주변 노드와 원래 클러스터의 중앙 노드를 연결하는 4개의 동일한 복제본을 만듭니다.이를 통해 25개의 노드(N = 25)의 네트워크를 얻을 수 있습니다.같은 프로세스를 반복하면 원래 클러스터의 복제본을 4개 더 만들 수 있습니다.각 4개의 주변 노드는 첫 번째 단계에서 작성한 노드의 중앙 노드에 연결됩니다.이 값은 N = 125이며 공정이 무한히 지속될 수 있습니다.

피트니스 모델

즉, 두 꼭지점 사이의 링크는 모든 꼭지점 쌍에 대해 확률 p가 동일한 랜덤하게 할당되지 않습니다.오히려 모든 정점 j에 대해 고유한 적합성_j x가 있으며, 정점 $i$와 j 사이의 링크는 확률${\displaystyle }$($xi, xj$^[37]로 작성된다. World Trade Web의 경우 국가 GDP의 적합성으로 모든 속성을 재구성하고, 이를 취하여

${{displaystyle p(x_i},x_{j}=black {black x_{i}x_{j}}{1+\black x_{i}x_{j}}}.}$^[38]

쌍곡선 기하학 그래프

네트워크가 기초가 되는 쌍곡선 지오메트리를 가지고 있다고 가정하면 공간 네트워크의 프레임워크를 사용하여 스케일 프리 도 분포를 생성할 수 있습니다.이 이종도 분포는 기본 쌍곡선 ^[39]기하학의 음의 곡률 및 메트릭 특성을 단순히 반영합니다.

원하는 속성을 가진 축척 자유 그래프를 생성하기 위한 모서리 이중 변환

저차상관계수와 군집계수의 스케일 프리 그래프부터 시작하여 에지-이중 변환을 ^[16]적용하여 훨씬 높은 차수의 상관계수와 군집계수를 가진 새로운 그래프를 생성할 수 있다.

균등 우선 부착 모델(UPA 모델)

UPA 모델은 리치 게인 시스템을 강조하는 우선 부가 메커니즘(확률 1-p)과 최신 노드에 대한 균일한 선택(확률 p)이라는 두 가지 부가 규칙을 고려하는 우선 부가 모델의 변형이다.이 수정은 학위 분포의 척도 없는 거동의 견고성을 연구하는 데 흥미롭다.점근적 멱함수 분포가 ^[26]보존된다는 것이 분석적으로 증명되었다.

확장성이 없는 이상적인 네트워크

네트워크 이론에서 스케일 프리 이상 네트워크는 스케일 프리 이상 가스 밀도 분포를 따르는 정도 분포를 갖는 랜덤 네트워크입니다.이들 네트워크는 ^[40][41]경쟁 클러스터 성장 과정을 네트워크에 적용하면 복잡한 네트워크 정보이론으로 사회집단의 규모 분포를 풀어내 도시 규모 분포와 선거 결과를 재현할 수 있다.스케일이 필요 없는 이상적인 네트워크 모델에서 던바의 숫자가 '6가지 분리도'로 알려진 현상의 원인이라는 것을 입증할 수 있다.

참신한 특징

n{n\displaystyle}노드와 바로 멱함수 지수 γ 을과scale-free 네트워크, 들어γ ′와 3{\displaystyle \gamma>3}, 이 유도 부분 그래프. 학위와 함께 vertices 로그⁡ n×로그보다 크∗⁡ n{\displaystyle \log{n}\times(^{*}{n}}에 의해 구성된scale-free 네트워크 x2{\displaystyle \gamma.'=2} $$거의 확실합니다.^[42]

멱함수 지수 추정

스케일 프리 네트워크의 멱함수$멱함수{\displaystyle }$ {\(\$displaystyle \gamma)$의 추정은 일반적으로 균등하게 샘플링된 소수의 노드의 ^[3]정도에 따른 최대우도 추정을 사용하여 이루어집니다.그러나 균일한 표본 추출은 멱함수 법칙 정도 분포의 중요한 헤비테일로부터 충분한 표본을 얻지 못하기 때문에 이 방법은 큰 치우침과 분산을 산출할 수 있습니다.최근 ^[43][44]우정 역설의 결과로 학위 분포의 꼬리 부분에서 올 가능성이 높은 무작위 친구(즉, 무작위 링크의 무작위 끝)를 표본으로 추출하는 것이 제안되었다.이론적으로 무작위 친구와의 최대우도 추정은 균일한 표본 ^[44]추출에 기초한 기존 접근법에 비해 더 작은 편중과 작은 분산을 초래한다.

「 」를 참조해 주세요.

• 랜덤 그래프 – 랜덤 프로세스에 의해 생성된 그래프
• Erdss-Rényi 모델– 랜덤 그래프 생성을 위한 밀접하게 관련된 두 가지 모델
• 비선형 우선 부착
• 보스-아인슈타인 응축(네트워크 이론)
• 스케일 불변성 – 길이 또는 에너지 척도에 공통 계수를 곱해도 변하지 않는 기능
• 복잡한 네트워크– 간단한 토폴로지 기능이 없는 네트워크
• 웹그래프
• 바라바시-알베르트 모형
• 비앙코니-바라바시 모형

레퍼런스

추가 정보

• Albert R.; Barabási A.-L. (2002). "Statistical mechanics of complex networks". Rev. Mod. Phys. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47. S2CID 60545.
• Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Classes of small-world networks". PNAS. 97 (21): 11149–52. arXiv:cond-mat/0001458. Bibcode:2000PNAS...9711149A. doi:10.1073/pnas.200327197. PMC 17168. PMID 11005838.
• Barabási, Albert-László (2004). Linked: How Everything is Connected to Everything Else. ISBN 0-452-28439-2.
• Barabási, Albert-László; Bonabeau, Eric (May 2003). "Scale-Free Networks" (PDF). Scientific American. 288 (5): 50–9. Bibcode:2003SciAm.288e..60B. doi:10.1038/scientificamerican0503-60. PMID 12701331.
• Dan Braha; Yaneer Bar-Yam (2004). "Topology of Large-Scale Engineering Problem-Solving Networks" (PDF). Phys. Rev. E. 69 (1): 016113. Bibcode:2004PhRvE..69a6113B. doi:10.1103/PhysRevE.69.016113. PMID 14995673. S2CID 1001176.
• Caldarelli G. "Scale-Free Networks" 옥스포드 대학 출판부, 옥스퍼드(2007).
• Caldarelli G.; Capocci A.; De Los Rios P.; Muñoz M.A. (2002). "Scale-free networks from varying vertex intrinsic fitness". Physical Review Letters. 89 (25): 258702. arXiv:cond-mat/0207366. Bibcode:2002PhRvL..89y8702C. doi:10.1103/PhysRevLett.89.258702. PMID 12484927.
• Dangalchev, Ch. (2004). "Generation models for scale-free networks". Physica A. 338 (3–4): 659–671. Bibcode:2004PhyA..338..659D. doi:10.1016/j.physa.2004.01.056.
• Dorogovtsev, S.N.; Mendes, J.F.F.; Samukhin, A.N. (2000). "Structure of Growing Networks: Exact Solution of the Barabási—Albert's Model". Phys. Rev. Lett. 85 (21): 4633–6. arXiv:cond-mat/0004434. Bibcode:2000PhRvL..85.4633D. doi:10.1103/PhysRevLett.85.4633. PMID 11082614. S2CID 118876189.
• Dorogovtsev, S.N.; Mendes, J.F.F. (2003). Evolution of Networks: from biological networks to the Internet and WWW. Oxford University Press. ISBN 0-19-851590-1.
• Dorogovtsev, S.N.; Goltsev A.V.; Mendes, J.F.F. (2008). "Critical phenomena in complex networks". Rev. Mod. Phys. 80 (4): 1275–1335. arXiv:0705.0010. Bibcode:2008RvMP...80.1275D. doi:10.1103/RevModPhys.80.1275. S2CID 3174463.
• Dorogovtsev, S.N.; Mendes, J.F.F. (2002). "Evolution of networks". Advances in Physics. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519. S2CID 429546.
• Erdős, P.; Rényi, A. (1960). On the Evolution of Random Graphs (PDF). Vol. 5. Publication of the Mathematical Institute of the Hungarian Academy of Science. pp. 17–61.
• Faloutsos, M.; Faloutsos, P.; Faloutsos, C. (1999). "On power-law relationships of the internet topology". Comp. Comm. Rev. 29 (4): 251–262. doi:10.1145/316194.316229.
• Li, L.; Alderson, D.; Tanaka, R.; Doyle, J.C.; Willinger, W. (2005). "Towards a Theory of Scale-Free Graphs: Definition, Properties, and Implications (Extended Version)". arXiv:cond-mat/0501169.
• Kumar, R.; Raghavan, P.; Rajagopalan, S.; Sivakumar, D.; Tomkins, A.; Upfal, E. (2000). "Stochastic models for the web graph" (PDF). Proceedings of the 41st Annual Symposium on Foundations of Computer Science (FOCS). Redondo Beach, CA: IEEE CS Press. pp. 57–65.
• Matlis, Jan (November 4, 2002). "Scale-Free Networks".
• Newman, Mark E.J. (2003). "The structure and function of complex networks". SIAM Review. 45 (2): 167–256. arXiv:cond-mat/0303516. Bibcode:2003SIAMR..45..167N. doi:10.1137/S003614450342480. S2CID 221278130.
• Pastor-Satorras, R.; Vespignani, A. (2004). Evolution and Structure of the Internet: A Statistical Physics Approach. Cambridge University Press. ISBN 0-521-82698-5.
• Pennock, D.M.; Flake, G.W.; Lawrence, S.; Glover, E.J.; Giles, C.L. (2002). "Winners don't take all: Characterizing the competition for links on the web". PNAS. 99 (8): 5207–11. Bibcode:2002PNAS...99.5207P. doi:10.1073/pnas.032085699. PMC 122747. PMID 16578867.
• 롭, 존Scale-Free Networks and Terroris, 2004.
• Keller, E.F. (2005). "Revisiting "scale-free" networks". BioEssays. 27 (10): 1060–8. doi:10.1002/bies.20294. PMID 16163729. Archived from the original on 2011-08-13.
• Onody, R.N.; de Castro, P.A. (2004). "Complex Network Study of Brazilian Soccer Player". Phys. Rev. E. 70 (3): 037103. arXiv:cond-mat/0409609. Bibcode:2004PhRvE..70c7103O. doi:10.1103/PhysRevE.70.037103. PMID 15524675. S2CID 31653489.
• Kasthurirathna, D.; Piraveenan, M. (2015). "Complex Network Study of Brazilian Soccer Player". Sci. Rep. In Press.