타원에 관한 뉴턴의 정리

Newton's theorem about ovals

수학에서, 타원에 관한 뉴턴의 정리는 매끄러운 볼록 타원형의 1초에 의해 잘리는 면적은 1초의 대수함수가 아니라는 것을 말합니다.

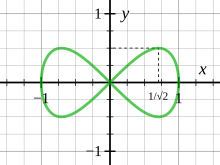
아이작 뉴턴은 뉴턴의 원리 1권의 6절의 보조정리 28이라고 말하고, 이를 이용해 궤도를 움직이는 행성의 위치가 시간의 대수함수가 아니라는 것을 보여주었습니다. 뉴턴이 타원형이 무엇을 의미하는지 정확히 언급하지 않았기 때문에 이 정리가 정확한지 아닌지에 대한 논란이 있었고, 타원형이라는 단어에 대한 어떤 해석에서는 이 정리가 정확한 반면, 다른 해석에서는 거짓이라는 논란이 있었습니다. 만약 "oval"가 단지 연속적인 닫힌 볼록 곡선을 의미한다면, 삼각형이나 Huygens lemniscate y = x - x 의 로브 중 하나와 같은 반례가 존재하는 반면, Arnold(1989)는 "oval"가 무한히 미분 가능한 볼록 곡선을 의미한다면 뉴턴의 주장이 옳으며 그의 주장은 엄격한 증명의 필수적인 단계를 가지고 있다고 지적했습니다.

바실리예프(2002)는 뉴턴의 정리를 더 높은 차원으로 일반화했습니다.

진술

제로노나 하위겐스의 렘니스케이트;초에 의해 잘려나간 영역은 대수적이지만, 렘니스케이트는 원점에서 매끄럽지 않습니다.

영어 번역 뉴턴의 원진술서(Newton 1962, 보조정리 28절 6권 I)는 다음과 같습니다.

"즐겁게 오른쪽 선으로 잘린 영역이 유한한 항과 차원의 방정식으로 보편적으로 발견될 수 있는 타원형 도형은 없습니다."

뉴턴은 현대 수학 언어에서 기본적으로 다음과 같은 정리를 증명했습니다.

볼록 매끄러운(무한 미분 가능한 것을 의미하는) 곡선이 없으므로 선 축 + = c에 의해 잘린 면적은 a, b, c의 대수 함수입니다.

즉, 뉴턴의 진술에서 "타원"은 "곡면 매끄러운 곡선"을 의미해야 합니다. 모든 점에서 무한한 미분 가능성이 필요합니다. 임의의 양의 정수 n에 대하여, 한 점을 제외하고는 전혀 매끄럽고 할 수 있는 대수적 곡선이 존재하며, 나머지 점에서 할 수 있는 영역이 대수적으로 단절된 부분은 n번 미분 가능합니다.

뉴턴은 비슷한 주장이 두 점 사이의 (평활한 볼록한) 타원의 호의 길이가 점들의 대수 함수에 의해 주어지지 않는다는 것을 보여준다고 관찰했습니다.

뉴턴의 증명

타원이 원점을 중심으로 한 원이라면 뉴턴이 만든 나선은 아르키메데스 나선입니다.

뉴턴은 타원형 안에서 원점 P를 취했고, 극좌표에서 점(r, θ)의 나선형을 고려했는데, 점 P로부터의 거리 r은 각도 0과 θ을 가진 P로부터의 선들에 의해 단절된 영역입니다. 그리고 그는 이 나선형이 P를 통과하는 선과 무한히 많은 교차점을 가지고 있기 때문에 대수적일 수 없으며, 따라서 초에 의해 잘린 영역은 초의 대수적 함수가 될 수 없다고 관찰했습니다.

이 증명을 위해서는 타원형과 따라서 나선형이 매끄러워야 합니다. 그렇지 않으면 나선형은 서로 다른 대수 곡선 조각들의 무한 결합일 수 있습니다. 매끄럽지 않은 타원에 대한 뉴턴의 정리에 대한 다양한 "반례"에서 일어나는 일입니다.

참고문헌

  • Arnold, V. I. (1989), "Topological proof of the transcendence of the abelian integrals in Newton's Principia", Istoriko-Matematicheskie Issledovaniya (31): 7–17, ISSN 0136-0949, MR 0993175
  • Arnold, V. I.; Vasilev, V. A. (1989), "Newton's Principia read 300 years later", Notices of the American Mathematical Society, 36 (9): 1148–1154, ISSN 0002-9920, MR 1024727
  • Newton, I. (1962), Florian Cajori (ed.), Principia Vol. I The Motion of Bodies, translated by Andrew Motte, Berkeley: University of California Press, ISBN 978-0-520-00928-8 뉴턴의 프린시피아의 이전(2차) 판본의 대체 번역.
  • Pesic, Peter (2001), "The validity of Newton's Lemma 28", Historia Mathematica, 28 (3): 215–219, doi:10.1006/hmat.2001.2321, ISSN 0315-0860, MR 1849799
  • Pourciau, Bruce (2001), "The integrability of ovals: Newton's Lemma 28 and its counterexamples", Archive for History of Exact Sciences, 55 (5): 479–499, doi:10.1007/s004070000034, ISSN 0003-9519, MR 1827869, S2CID 119853564
  • Vassiliev, V. A. (2002), Applied Picard-Lefschetz theory, Mathematical Surveys and Monographs, vol. 97, Providence, R.I.: American Mathematical Society, doi:10.1090/surv/097, ISBN 978-0-8218-2948-6, MR 1930577