뉴턴의 공전 궤도 정리

고전역학에서 뉴턴의 회전 궤도 정리는 입자의 각속도에 k배율을 곱하는 데 필요한 중심 힘의 종류를 결정합니다(그림 1, 2). 뉴턴은 그의 정리를 달과 행성에 대해 관측되는 궤도의 전체적인 회전을 이해하는 데 적용했습니다(아프시달 세차, 그림 3). "반지름 운동"이라는 용어는 힘의 중심을 향하거나 그로부터 멀어지는 운동을 의미하는 반면, 각운동은 반지름 운동에 수직입니다.

아이작 뉴턴은 1687년에 처음 출판된 그의 철학 æ 자연 원리 수학의 제1권의 명제 43–45에서 이 정리를 도출했습니다. 제안 43에서 그는 추가된 힘은 입자와 공간에 고정된 점(중심) 사이의 거리 r에만 의존하는 중심 힘이어야 한다는 것을 보여주었습니다. 명제 44에서 그는 힘에 대한 공식을 유도하여 r의 역큐브로 변하는 역큐브 힘임을 보여주었습니다. 제안서 45에서 뉴턴은 입자가 거의 원형 궤도로 이동한다고 가정함으로써 임의의 중심 힘으로 정리를 확장했습니다.

천체 물리학자 Subrahmanyan Chandrasekar가 뉴턴의 원리에 대한 1995년 논평에서 언급했듯이, 이 정리는 3세기 이상 동안 거의 알려지지 않았고 개발되지 않은 채로 남아 있었습니다.^[1] 1997년 이래로, 그 정리는 Donald Lynden-Bell과 공동 연구자들에 의해 연구되어 왔습니다.^[2][3] 최초의 정확한 확장은 2000년에 Mahomed and Vawda의 작업으로 이루어졌습니다.^[4]

역사적 맥락

천체의 운동은 수천 년 동안 체계적으로 연구되어 왔습니다. 그 별들은 항상 서로 같은 상대적 위치를 유지하면서 균일하게 회전하는 것이 관찰되었습니다. 그러나 다른 천체들은 고정된 별들을 배경으로 떠돌아다니는 것이 관측되었는데, 대부분의 천체들은 그리스어로 "유랑자들"을 뜻하는 πλα νήτοι(plan ētoi)의 이름을 따서 행성이라고 불렸습니다. 일반적으로 하늘을 가로지르는 경로(황도)를 따라 같은 방향으로 움직이지만, 개별 행성들은 때때로 방향을 짧게 반전시켜 역행 운동을 보여줍니다.^[5]

이 앞뒤 움직임을 설명하기 위해, 페르가의 아폴로니우스 (c. 262 – c. 190 BC)는 방어자와 에피사이클의 개념을 개발했고, 이에 따라 행성은 다른 회전하는 원을 타고 이동합니다. 이 접근법은 현대 푸리에 변환에 해당하기 때문에 어떤 궤도든 충분한 수의 신중하게 선택된 에피사이클로 설명할 수 있습니다.^[6] 약 350년 후, 클라우디우스 프톨레마이오스는 그의 Almagest를 출판했고, 그는 그의 시대 최고의 천문학적 관측에 걸맞게 이 시스템을 개발했습니다. 에피사이클을 설명하기 위해 프톨레마이오스는 행성이 동심 회전하는 구에 국한된 아리스토텔레스의 지구 중심 우주론을 채택했습니다. 이 우주 모형은 거의 1500년 동안 권위적이었습니다.

행성 운동에 대한 현대적인 이해는 16세기 천문학자 Tycho Brahe와 물리학자 Johannes Kepler의 결합된 노력에서 비롯되었습니다. 타이코는 행성 운동의 매우 정확한 측정으로 인정받고 있으며, 이로부터 케플러는 행성 운동의 법칙을 도출할 수 있었습니다.^[7] 이 법칙들에 따르면, 행성들은 태양 주위를 회전하는 타원형(심주기가 아닌)으로 이동합니다. 케플러의 두 번째 법칙과 세 번째 법칙은 구체적인 정량적 예측을 합니다: 행성은 같은 시간에 같은 면적을 휩쓸고, 궤도 주기의 제곱은 고정 상수의 반 장축의 세제곱과 같습니다.^[8] 이후 행성 궤도를 관측한 결과 타원의 장축(이른바 apsides line)이 시간에 따라 점차 회전하는 것으로 나타났으며, 이 회전을 apsidal precession이라고 합니다. 궤도의 통로는 궤도를 도는 물체가 끌어당기는 중심에서 가장 가깝거나 가장 멀리 떨어져 있는 지점입니다. 태양 주위를 도는 행성의 경우, 통로는 근일점(가장 가까운)과 원일점(가장 먼)에 해당합니다.^[9]

그로부터 약 80년 후(1687년), 아이작 뉴턴은 케플러의 세 가지 법칙을 모두 설명하는 물리 이론을 제공했는데, 이 이론은 뉴턴의 운동 법칙과 만유인력 법칙에 기초한 이론입니다. 특히 뉴턴은 두 물체 사이의 중력이 두 물체 사이의 거리 r의 역제곱으로 변하는 중심 힘 F(r)이라고 제안했습니다. 뉴턴은 그의 운동 법칙에서 주장하며, 그러한 힘 하나에 의해 작용하는 입자의 궤도는 항상 원뿔의 단면이며, 특히 무한대로 가지 않는 경우 타원임을 보여주었습니다. 그러나 이 결론은 두 개의 물체가 존재할 때만 성립합니다. 세 개 이상의 물체가 상호 중력 하에서 작용하는 운동(n체 문제)은 ^[10][11]뉴턴 이후 몇 세기 동안 해결책이 발견되었지만 해결되지 않은 채로 남아 있었습니다.^[12] 뉴턴은 태양의 중력이 지배적이기 때문에 태양 주위의 행성들의 궤도는 대체로 타원형이라고 제안했습니다. 첫 번째 근사치에 따르면 다른 행성들의 존재는 무시될 수 있습니다. 비유하자면, 지구 주위를 도는 달의 타원 궤도는 지구 중력에 의해 지배되었습니다. 첫 번째 근사치로 태양의 중력과 태양계의 다른 물체들의 중력은 무시될 수 있습니다. 그러나 뉴턴은 행성 궤도와 달 궤도의 점진적인 아피달 세차는 이러한 무시된 상호작용의 영향 때문이라고 말했습니다. 특히 달 궤도의 세차는 태양과의 중력 상호작용의 교란 효과 때문이라고 말했습니다.^[13]

뉴턴의 회전 궤도 정리는 아피달 세차를 정량적으로 이해하려는 그의 첫 번째 시도였습니다. 이 정리에 따르면 특정 유형의 중심 힘인 역-큐브 힘을 더하면 회전 궤도를 만들 수 있습니다. 각속도에 k를 곱한 반면 방사 운동은 변하지 않습니다. 그러나 이 정리는 관련이 없을 수도 있는 특정 유형의 힘으로 제한됩니다. 여러 교란 역제곱 상호작용(예: 다른 행성의 상호작용)은 역큐브 힘과 정확히 합할 것 같지 않습니다. 그의 정리를 다른 유형의 힘에도 적용할 수 있도록 하기 위해 뉴턴은 태양계의 대부분의 궤도에서 실제로 그렇듯이 거의 원형 궤도, 즉 이심률이 낮은 타원 궤도의 한계에서 임의의 중심 힘 F(r)의 역-큐브 전위에 대한 최상의 근사치를 발견했습니다. 이러한 근사를 찾기 위해 뉴턴은 테일러 전개의 전신으로 볼 수 있는 무한급수를 개발했습니다.^[14] 이 근사를 통해 뉴턴은 임의의 중심력에 대한 세차운동의 비율을 추정할 수 있었습니다. 뉴턴은 이 근사치를 달 궤도의 정점 세차를 일으키는 힘의 모델을 시험하는 데 적용했습니다. 하지만, 달의 운동에 대한 문제는 엄청나게 복잡하며, 뉴턴은 달의 반달 세차에 대한 정확한 중력 모델을 발표하지 않았습니다. 1747년에 Clairaut에 의해 더 정확한 모델이 만들어진 후,^[15] 달의 움직임에 대한 분석적인 모델은 Hill,^[16] Brown,^[17] Delaunay에 의해 19세기 후반에 개발되었습니다.^[18]

그러나 뉴턴의 정리는 단순한 아피달 세차를 설명하는 것보다 더 일반적입니다. 그것은 뉴턴의 만유인력의 법칙이나 쿨롱의 법칙과 같은 역제곱 힘뿐만 아니라 어떤 중심 힘 F(r)에도 역큐브 힘을 더하는 효과를 설명합니다. 뉴턴의 정리는 고전역학에서 역-큐브 힘을 고려에서 제거함으로써 궤도 문제를 단순화합니다. 방사상 운동과 각운동, r(t)와 θ(t)는 역-큐브 힘 없이도 계산할 수 있고, 그 효과는 입자의 각속도를 곱하여 계산할 수 있습니다.

${\displaystyle \omega_{2}={\frac {d\theta_{2}}{dt}}=k{\frac {d\theta_{1}}{dt}}=k\omega_{1}}$

수학문

임의의 중심 힘 F(r) 아래에서 움직이는 입자의 크기는 입자와₁ 고정된 중심 사이의 거리 r에만 의존한다고 생각합니다. 중심 힘을 받는 입자의 운동은 항상 평면에 있기 때문에 입자의 위치는 극좌표(r, θ), 힘의 중심에 대한 입자의 반지름과 각도로 설명할 수 있습니다(그림 1). 이 두 좌표인 r(t)와 θ(t)는 입자가 움직일 때 시간 t에 따라 변합니다.

질량 m이 같고 반지름 운동이 r(t)인 두 번째 입자를 상상해 보세요. 그러나 각속도가 첫 번째 입자보다 k배 빠른 입자를 상상해 보세요. 즉, 두 입자의 방위각은 방정식 θ(t) = k θ(t)에 의해 관련됩니다. 뉴턴은 두 번째 입자의 운동이 첫 번째 입자에^[19] 작용하는 힘₁ F(r)에 역-큐브 중심 힘을 더함으로써 생성될 수 있음을 보여주었습니다.

${\displaystyle F_{2}(r)-F_{1}(r)={\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)}$

여기서 L은₁ 중심력에 대한 운동 상수(보존된)인 첫 번째 입자의 각운동량의 크기입니다.

k가² 1보다 크면 F₂ - F는₁ 음수입니다. 따라서 추가된 역-큐브 힘은 그림 1-4와 그림 9의 녹색 행성에서 관찰된 것과 같이 매력적입니다. 반대로, k가² 1보다 작으면 F-F는₂₁ 양수입니다. 추가된 역-큐브 힘은 그림 5와 그림 10의 녹색 행성과 그림 4와 그림 5의 적색 행성에서 관찰된 것처럼 반발력을 갖습니다.

입자 경로 변경

이러한 역-큐브 힘의 추가는 입자가 뒤따르는 경로를 변경하기도 합니다. 입자의 경로는 r(t) 및 θ(t)와 같은 반경 및 각도 운동의 시간 의존성을 무시하고 오히려 반경 및 각도 변수를 서로 연관시킵니다. 이를 위해 각도 변수는 제한이 없으며 입자가 중심점을 여러 번 회전함에 따라 무한히 증가할 수 있습니다. 예를 들어, 입자가 중심점을 중심으로 두 바퀴 돌고 시작 위치로 돌아오면 최종 각도는 초기 각도와 같지 않고 오히려 2×360°=720° 증가했습니다. 형식적으로 각도 변수는 각속도의 적분으로 정의됩니다.

${\displaystyle \theta_{1}\equiv \int \omega_{1}(t)\,dt.}$

비슷한 정의는 두 번째 입자의 각도인 θ를 의미합니다.

첫 번째 입자의 경로를 r = g(θ)의 형태로 기술하면 θ = k θ이므로 두 번째 입자의 경로는 함수 r = g(θ/k)에 의해 제공됩니다. 예를 들어, 첫 번째 입자의 경로를 타원이라고 가정합니다.

${\displaystyle {\frac {1}{r}}=A+B\cos \theta _{1}}$

여기서 A와 B는 상수이고, 두 번째 입자의 경로는 다음에 의해 주어집니다.

${\displaystyle {\frac {1}{r}}=A+B\cos \left ({\frac {\theta _{2}}{k}\right)}$

궤도 세차

k가 1에 가깝지만 같지 않은 경우, 두 번째 궤도는 첫 번째 궤도와 비슷하지만 힘의 중심을 중심으로 점차 회전합니다. 이를 궤도 세차라고 합니다(그림 3). k가 1보다 크면 궤도는 궤도와 같은 방향으로 진행하고(그림 3), k가 1보다 작으면 궤도는 반대 방향으로 진행합니다.

그림 3의 궤도가 균일하게, 즉 일정한 각속도로 회전하는 것처럼 보일 수 있지만, 이는 원궤도에만 해당됩니다.^[2][3] 궤도가 각속도 ω으로 회전하면 두 번째 입자의 각속도는 첫 번째 입자의 각속도보다 ω만큼 빠르거나 느립니다. 즉, 각속도는 방정식 ω = ω + ω ω를 만족합니다. 그러나 뉴턴의 회전 궤도 정리에 따르면 각속도는 곱셈과 관련이 있습니다: ω = k ω, 여기서 k는 상수입니다. 이 두 방정식을 결합하면 세차의 각속도가 ω = (k - 1) ω와 같다는 것을 알 수 있습니다. 따라서 ω이 일정한 경우에만 ω이 일정합니다. 각운동량 보존에 따라 반지름 r에 따라 ω가 변합니다.

${\displaystyle \omega_{1}={\frac {L_{1}}{mr^{2}};}$

여기서 m과 L은₁ 각각 첫 번째 입자의 질량과 각운동량이며 둘 다 일정합니다. 따라서 ω은 반지름 r이 일정할 때, 즉 궤도가 원일 때에만 일정합니다. 하지만 그 경우 궤도는 진행하면서 변하지 않습니다.

예시적인 예: 코테스의 나선형

뉴턴 정리의 가장 간단한 예는 초기 힘, 즉 F(r) = 0이 없을 때 발생합니다. 이 경우 첫 번째 입자는 정지해 있거나 직선으로 이동합니다. 원점(그림 6의 노란색 선)을 통과하지 않는 직선으로 진행하는 경우, 해당 선에 대한 방정식은 극좌표(r, θ)에 다음과 같이 표기될 수 있습니다.

${\displaystyle {\frac {1}{r}}={\frac {1}{b}}\cos \ (\theta _{1}-\theta _{0})}$

여기서 θ는 거리가 최소가 되는 각도입니다(그림 6). 거리 r은 무한대(θ – θ = -90°일 때)에서 시작하여 거리가 최소가 될 때 θ – θ = 0°까지 점차 감소하다가 θ – θ = 90°에서 다시 무한대로 점차 증가합니다. 최소 거리 b는 충격 파라미터로 고정된 중심에서 운동선까지의 수직인 길이로 정의됩니다. 역-큐브 중심 힘이 추가될 때도 동일한 방사 운동이 가능합니다.

역-큐브 중심 힘 F₂(r)는 다음과 같은 형태를 갖습니다.

${\displaystyle F_{2}(r)={\frac {\mu }{r^{3}}}}$

여기서 분자 μ는 양(반발적) 또는 음(attract적)일 수 있습니다. 만약 이러한 역-큐브 힘이 도입된다면, 뉴턴의 정리는 대응하는 해들이 코테스의 나선형이라고^{[clarification needed]} 불리는 형태를 갖는다고 말합니다. 이들은 방정식으로^[20][21] 정의되는 곡선입니다.

${\displaystyle {\frac {1}{r}}={\frac {1}{b}}\cos \left ({\frac {\theta _{2}-\theta _{0}{k}\right)}$

상수 k가 같은 경우

${\displaystyle k^{2}=1-{\frac {m\mu }{L_{1}^{2}}}}$

방정식의 우변이 양의 실수일 때, 해는 에피스파이럴에 해당합니다.^[22] 인수 θ – θ이 ±90°×k와 같을 때 코사인은 0이 되고 반지름은 무한대가 됩니다. 따라서 k가 1보다 작으면 허용 각도의 범위가 작아지고 힘이 반발하게 됩니다(그림 7의 오른쪽 빨간색 곡선). 반면 k가 1보다 크면 허용 각도의 범위가 증가하여 인력(그림 7에서 왼쪽의 녹색, 청록색 곡선)에 해당하며, 입자의 궤도는 중심을 여러 번 감쌀 수도 있습니다. 파라미터 k의 가능한 값들은 0부터 무한대의 범위일 수 있고, 이는 음의 무한대부터 양의 상한, L₁²/m까지의 μ의 값들에 대응합니다. 따라서 모든 매력적인 역-큐브 힘(음의 μ)에 대해 그림 7과 같이 일부 반발력(μ₁² < L/m)에 대해 해당하는 에피스파이럴 궤도가 있습니다. 더 강한 반발력은 더 빠른 직선 운동에 해당합니다.

다른 솔루션 유형 중 하나는 쌍곡선 코사인으로 표시됩니다.

${\displaystyle {\frac {1}{r}}={\frac {1}{b}}\cosh \ \left ({\frac {\theta _{0}-\theta _{2}}{\lambda }\right)}$

일정한 λ이 만족하는 곳에서

${\displaystyle \lambda ^{2}={\frac {m\mu}{L_{1}^{2}}-1}$

이러한 형태의 코테스의 나선은 포인소트의 나선 2개 중 하나에 해당합니다(그림 8).^[22] 가능한 λ 값의 범위는 0부터 무한대까지이며, 이 값은 양수 L/m보다 큰 μ의 값에 해당합니다. 따라서, 포인소 나선 운동은 반발 역-큐브 중심 힘에 대해서만 발생하며, L이 주어진 μ에 비해 너무 크지 않은 경우에 적용됩니다.

k 또는 λ의 극한을 0으로 취하면 코테스 나선의 세 번째 형태, 이른바 역 나선 또는 쌍곡 나선이 해로 나타납니다.

${\displaystyle {\frac {1}{r}}=A\theta _{2}+\varepsilon }$

여기서 A와 ε는 임의의 상수입니다. 이러한 곡선은 반발력의 세기 μ가 각운동량-질량항과 정확히 일치할 때 발생합니다.

${\displaystyle \mu = {\frac {L_{1}^{2}}{m}}$

닫힌 궤도와 역-큐브 중심 힘

후크의 법칙과 같이 거리에 따라 선형적으로 증가하는 F = Cr, 뉴턴의 만유인력의 법칙과 쿨롱의 법칙과 같은 역제곱 힘, F = C/r의 두 종류의 중심 힘은 매우 특이한 성질을 가지고 있습니다. 두 종류의 힘 중에서 움직이는 입자는 무한대로 이동할 수 있는 충분한 에너지가 없다면 항상 초기 속도와 함께 출발지로 되돌아갑니다. 즉, 결합된 입자의 경로는 초기 위치나 속도에 상관없이 항상 닫혀 있고 움직임은 무한히 반복됩니다. 베르트랑의 정리에서 알 수 있듯이, 이 성질은 다른 종류의 힘에 대해서는 사실이 아닙니다. 일반적으로 입자는 같은 속도로 출발점으로 되돌아가지 않습니다.

그러나 뉴턴의 정리는 k가 유리수와 같다면 궤도가 닫힌 상태로 유지되도록 직선 또는 역제곱 힘 아래에서 움직이는 입자에 역입방 힘이 작용할 수 있음을 보여줍니다. (숫자를 m/n 분수로 쓸 수 있다면 "합리적"이라고 합니다. 여기서 m과 n은 정수입니다.) 이러한 경우에 역-입방 힘의 추가는 원래 입자가 n회전을 완료하는 동시에 입자가 힘의 중심에 대해 m회전을 완료하도록 합니다. 폐쇄 궤도를 생성하는 이 방법은 추가된 역-입방 힘이 입자의 초기 속도에 의존하기 때문에 베르트랑의 정리를 위반하지 않습니다.

고조파 및 부조화 궤도는 그러한 폐쇄 궤도의 특별한 유형입니다. 닫힌 궤적은 k가 정수일 경우, 즉 공식 k = m/n에서 n = 1일 경우 조화 궤도라고 불립니다. 예를 들어, k = 3일 경우(그림 1 및 4의 녹색 행성, 그림 9의 녹색 궤도), 결과적인 궤도는 원래 궤도의 세 번째 고조파입니다. 반대로, 만약 k가 정수의 역수라면, 즉 공식 k = m/n에서 m = 1이면, 닫힌 궤도를 서브하모닉 궤도라고 부릅니다. 예를 들어, k = 1/3 (그림 5의 녹색 행성, 그림 10의 녹색 궤도)일 경우, 그 결과 생성된 궤도를 원래 궤도의 세 번째 서브하모닉이라고 합니다. 그러한 궤도는 자연계에서 발생할 가능성은 거의 없지만 뉴턴의 정리를 설명하는 데 도움이 됩니다.^[2]

원에 가까운 궤도의 한계

뉴턴은 그의 프린키피아 제45호에서 회전 궤도 정리를 적용하여 행성의 운동을 지배하는 힘 법칙을 찾는 방법을 개발했습니다.^[24] 요하네스 케플러는 대부분의 행성과 달의 궤도는 타원으로 보이며, 그 타원의 장축은 천문학적 측정으로부터 정확하게 결정될 수 있다고 언급했습니다. 장축은 최소 및 최대 거리의 위치를 중심점에 연결하는 선, 즉 두 개의 통로를 연결하는 선으로 정의됩니다. 예를 들어 수성의 장축은 근일점과 근일점의 연속적인 위치를 지나는 선으로 정의됩니다. 시간이 지남에 따라 대부분의 궤도를 도는 물체의 장축은 다른 물체의 중력 섭동, 인력체의 편평성, 일반 상대론적 효과 및 기타 효과로 인해 일반적으로 완전한 회전당 몇 도 이하로 점진적으로 회전합니다. 뉴턴의 방법은 이 아피달 세차를 행성에 가해지는 힘의 종류에 대한 민감한 프로브로 사용합니다.^[25]

뉴턴의 정리는 역-큐브 중심 힘을 더하는 효과만을 설명합니다. 그러나 뉴턴은 태양계의 8개 행성 궤도 중 7개에 해당하는 궤도 이심률(ε ≤0.1)이 낮은 타원과 같이 거의 원형에 가까운 궤도에 주의를 제한함으로써 임의의 중심력 F(r)로 정리를 확장합니다. 뉴턴은 또한 자신의 정리를 이심률 ε이 약 0.21인 수성에 적용하여 궤도 이심률이 약 0.97인 핼리 혜성과 관련이 있을 수 있다고 제안했습니다.

발루리, 윌슨, 하퍼는 그의 방법에 대한 이 외삽에 대한 정성적인 정당성을 제안했습니다.^[25] 그들의 주장에 따르면, 뉴턴은 apsidal precession angle α(중심으로부터의 연속적인 최소 거리와 최대 거리의 벡터 사이의 각도)를 궤도 이심률 ε의 매끄럽고 연속적인 함수로 여겼습니다. 역제곱 힘의 경우 α는 180°와 같습니다. 최소 거리와 최대 거리의 위치에 대한 벡터는 동일한 선에 놓여 있습니다. 처음에 α가 낮은 ε(quasi-circular 궤도)에서 180°가 아닌 경우 일반적으로 α는 고립된 ε 값에 대해서만 180°와 같아집니다. 무작위로 선택된 ε 값은 α = 180°를 제공할 가능성이 매우 낮습니다. 따라서 행성 궤도의 정점의 느린 회전은 중력이 역제곱 법칙임을 암시합니다.

정량식

방정식을 단순화하기 위해 뉴턴은 F(r)을 새로운 함수 C(r)로 씁니다.

${\displaystyle F(r)={\frac {C(r)}{Rr^{3}}}$

여기서 R은 원에 가까운 궤도의 평균 반지름입니다. 뉴턴은 C(r)를 (현재 테일러 팽창으로 알려진) 급수에서 거리 r의 거듭제곱으로 확장하며, 이는 그러한 급수의 첫 번째 등장 중 하나입니다.^[27] 결과적인 역-큐브 힘 항을 회전 궤도에 대한 역-큐브 힘과 동일시함으로써 뉴턴은 거의 원형 궤도에 대해 동등한 각도 스케일링 계수 k를 도출합니다.^[24]

${\displaystyle {\frac {1}{k^{2}}=\left ({\frac {R}{C}}\right)\left.{\frac {dC}{dr}}\right _{r=R}}$

즉, 거의 원형 타원 궤도에 임의의 중심 힘 F(r)를 적용하면 방사 운동에 큰 영향을 미치지 않고 k 인자에 의한 각운동을 가속시킬 수 있습니다. 타원 궤도가 정지해 있으면 입자는 장축의 한쪽 끝에서 다른 쪽 끝으로 이동하면서 힘의 중심을 기준으로 180° 회전합니다(두 개의 aps). 따라서 일반적인 중심 힘에 대한 대응하는 압살각 α는 일반적인 법칙 θ = k θ을 사용하여 k×180°와 같습니다.

예

뉴턴은 세 가지 예를 들어 자신의 공식을 설명합니다. 처음 두 개에서 중심 힘은 거듭제곱 법칙인 F(r) = r이므로 C(r)은 r에 비례합니다. 위의 공식은 각운동량에 k = 1/ √n의 계수를 곱한 것이며, 이에 따라 압시달 각도 α는 180°/ √n과 같음을 나타냅니다.

이 각도 스케일링은 apsidal precession, 즉 타원의 장축의 점진적인 회전에서 확인할 수 있습니다(그림 3). 위에서 언급한 바와 같이, 궤도 전체는 평균 각속도 ω ω = (k-1)로 회전하며, 여기서 ω은 고정 타원에 대한 입자의 평균 각속도와 같습니다. 입자가 한 apse에서 다른 apse로 이동하는 데 시간 T가 필요한 경우, 이는 동시에 장축이 각도 β = ωT = (k - 1) ωT = (k - 1) × 180°만큼 회전한다는 것을 의미합니다. 뉴턴의 만유인력 법칙과 같은 역제곱 법칙의 경우, n은 1이고 각도 스케일링이 없으며(k = 1), 안와각 α는 180°이며 타원 궤도는 정지 상태입니다(ω = β = 0).

마지막 예로 뉴턴은 두 멱함수 법칙의 합을 고려합니다.

${\displaystyle C(r)\propto ar^{m}+br^{n}}$

각속도에 인자를 곱한 값.

${\displaystyle k={\sqrt {\frac {a+b}{am+bn}}}}$

뉴턴은 이 두 공식( 거듭제곱 법칙과 두 거듭제곱 법칙의 합)을 모두 적용하여 달 궤도의 정점 세차를 조사합니다.

달 궤도의 세차운동

달의 움직임은 정확하게 측정될 수 있고, 행성의 움직임보다 눈에 띄게 복잡합니다.^[28] 고대 그리스 천문학자 히파르코스와 프톨레마이오스는 궤도 이심률의 작은 진동과 궤도의 황도면 기울기와 같은 ^[28]달 궤도의 주기적 변화에 주목했습니다. 이러한 진동은 일반적으로 한 달에 한 번 또는 두 번의 시간 척도로 발생합니다. 그것의 통로 선은 약 8.85년의 주기로 서서히 펴지는 반면, 그것의 마디 선은 그 시기의 약 두 배인 18.6년 만에 완전한 원을 만듭니다.^[29] 이것은 약 18년 주기의 일식, 이른바 사로스 주기를 설명합니다. 그러나 두 라인 모두 월별 시간 척도에서 움직임의 작은 변동을 경험합니다.

1673년, 제레미야 호록스는 달이 타원 궤도를 앞선다고 가정한 달의 운동에 대한 비교적 정확한 모델을 발표했습니다.^[30][31] 달의 움직임을 충분히 정확하고 간단하게 예측할 수 있는 방법이라면 배의 경도를 결정하는 항해상의 문제를 해결할 수 있었을 것입니다.^[32] 뉴턴의 시간에 목표는 달의 위치를 지상 경도의 1° 오차에 해당하는 2'(2호-분)로 예측하는 것이었습니다.^[33] 호록스의 모델은 달의 위치를 10 아크분 이하의 오차로 예측했습니다.^[33] 비교를 위해, 달의 지름은 대략 30 아크분 정도입니다.

뉴턴은 궤도 회전에 대한 정리를 두 가지 방법으로 사용하여 달의 정점 세차를 설명했습니다.^[34] 첫째, 그는 중력의 힘 법칙을 역제곱 법칙에서 지수가 2+4/243(약 2.0165)^[35]인 거듭제곱 법칙으로 변경함으로써 달의 관측된 아피달 세차를 설명할 수 있음을 보여주었습니다.

${\displaystyle F(r)=-{\frac {GMm}{r^{2+4/243}}}}$

1894년, 아사프 홀은 1859년 우르뱅 르 베리에가 관측한 ^[36]수성의 비정상적인 궤도 세차를 설명하기 위해 역제곱 법칙의 지수를 약간 수정하는 이 접근법을 채택했습니다.^[37] 아이러니하게도, 홀의 이론은 달에 대한 세심한 천문 관측에 의해 배제되었습니다.^[38] 이 세차에 대한 현재 받아들여지는 설명은 일반 상대성 이론을 포함합니다. 일반 상대성 이론은 (첫 번째 근사치에) 역 사분위수 힘, 즉 거리의 역 4제곱으로 변화하는 힘을 추가합니다.^[39]

뉴턴은 달의 세차 운동을 설명하기 위한 두 번째 접근법으로 달의 운동에 대한 태양의 교란 영향은 추가적인 선력과 거의 동일할 수 있다고 제안했습니다.

${\displaystyle F(r)={\frac {A}{r^{2}}+Br}$

첫 번째 항은 달과 지구 사이의 중력 인력에 해당하며, 여기서 r은 달과 지구 사이의 거리입니다. 뉴턴이 추론한 두 번째 항은 태양 중력이 지구-달계를 휘젓는 평균 힘을 나타낼 수 있습니다. 만약 지구가 균일한 밀도의 구형 먼지 구름으로 둘러싸여 있다면, 그러한 힘의 법칙은 결과적으로 나타날 수도 있습니다.^[40] 거의 원형 궤도에 대한 k의 공식과 A와 B의 추정치를 사용하여 뉴턴은 예측된 꼭짓점 각도 α가 (≈ 180.76°)이기 때문에 이 힘 법칙이 달의 세차운동을 설명할 수 없음을 보여주었습니다. 관측된 α(≈ 181.525°)보다. 모든 회전에서 장축은 관측된 3.^[34]0°의 약 절반인 1.5° 회전합니다.

일반화

아이작 뉴턴은 1687년에 그의 정리를 그의 철학 æ 자연주의 원리 수학의 제1권의 명제 43-45로서 처음 출판했습니다. 그러나 천체 물리학자 수브라흐만얀 찬드라세카르가 1995년 뉴턴의 원리에 대한 논평에서 언급했듯이, 이 정리는 3세기 이상 동안 거의 알려지지 않았고 개발되지 않은 채로 남아 있었습니다.^[1]

2000년에 마호메드와 보다는 뉴턴 정리의 첫 번째 일반화를 발견했습니다.^[4] 뉴턴이 그랬던 것처럼, 그들은 두 번째 입자의 각운동이 첫 번째 입자인 θ =k θ의 각운동보다 k배 더 빠르다고 가정했습니다. 그러나 뉴턴과는 대조적으로 마호메드와 보다는 두 입자의 반지름 운동이 r=r일 필요는 없었습니다. 오히려 그들은 역반지름이 일차방정식에 의해 관련되어 있을 것을 요구했습니다.

${\displaystyle {\frac {1}{r_{2}(t)}}={\frac {a}{r_{1}(t)}}+b}$

변수의 이러한 변환은 입자의 경로를 변경합니다. 첫 번째 입자의 경로를 r = g(θ)로 표기하면 두 번째 입자의 경로를 다음과 같이 표기할 수 있습니다.

${\displaystyle {\frac {ar_{2}}{1-br_{2}}=g\left ({\frac {\theta_{2}}{k}\right)}$

첫 번째 입자의 운동이 중심₁ 힘 F(r)에 의해 생성된다면, Mahomed와 Vawda는 두 번째 입자의 운동이 다음 힘에 의해 생성될 수 있음을 보여주었습니다.

${\displaystyle F_{2}(r_{2})={\frac {a^{3}}{\left(1-br_{2}\right)^{2}}}F_{1}\left({\frac {ar_{2}}{1-br_{2}}}\right)+{\frac {L^{2}}{mr^{3}}}\left(1-k^{2}\right)-{\frac {bL^{2}}{mr^{2}}}}$

이 방정식에 따르면 두 번째 힘 F₂(r)는 첫 번째 힘의 크기를 조정하고 인수를 변경하고 역제곱 및 역큐브 중심 힘을 추가하여 얻어집니다.

비교를 위해 뉴턴의 회전 궤도 정리는 경우 a = 1과 b = 0에 해당하므로 r = r입니다. 이 경우 원래 힘은 크기 조정되지 않고 인수는 변경되지 않습니다. 역-큐브 힘은 추가되지만 역-제곱 항은 추가되지 않습니다. 또한 두 번째 입자의 경로는 위의 공식과 일치하는 r = g(θ/k)입니다.

도함수

뉴턴 도함수

뉴턴의 유도는 그의 원칙 제9절, 구체적으로는 명제 43~45에 나와 있습니다.^[41] 그의 이러한 명제의 파생은 주로 기하학에 기초하고 있습니다.

제안 43; 문제 30

정지한 상태에서 다른 물체와 마찬가지로 힘의 중심을 중심으로 회전하는 곡선에서 물체를 움직이게 하는 것이 필요합니다.^[42]

뉴턴의 명제 43의 유도는 앞서 프린키피아에서 유도된 그의 명제 2에 달려 있습니다.^[43] 명제 2는 점 질량(입자)에 작용하는 알짜 힘이 중심 힘인지에 대한 기하학적 검정을 제공합니다. 뉴턴은 입자가 중심에서 측정한 것과 같은 시간에 같은 면적을 쓸어낼 경우에만 힘이 중심이라는 것을 보여주었습니다.

뉴턴의 유도는 입자가 임의의 중심 힘 F(r) 아래에서 움직이는 것으로 시작됩니다. 이 힘 아래에서 입자의 운동은 시간의 함수로서 중심으로부터의 반지름 r(t)와 각도 θ(t)로 설명됩니다. 무한히 작은 시간 dt에서 입자는 넓이가 다음과 같은 대략적인 직각삼각형을 쓸어내립니다.

${\displaystyle dA_{1}={\frac {1}{2}}r^{2}d\theta _{1}}$

입자에 작용하는 힘은 중심력이라고 가정하기 때문에, 뉴턴의 명제 2에 의해 입자는 같은 시간에 등각을 쓸어내립니다. 다른 방법으로 표현하면, 면적을 쓸어내는 속도는 일정합니다.

${\displaystyle {\frac {dA_{1}}{dt}}={\frac {1}{2}}r^{2}{\frac {d\theta _{1}}}=\mathrm {constant}$

이 일정한 면적 속도는 다음과 같이 계산할 수 있습니다. 정점과 근일점에서 인력 중심으로부터 가장 가까운 거리와 가장 먼 거리의 위치, 속도와 반지름 벡터는 수직이므로 입자의₁ 질량 m당 각운동량 L은₁ 영역을 쓸어버리는 속도와 관련이 있을 수 있습니다.

${\displaystyle h_{1}={\frac {L_{1}}{m}}=rv_{1}=r^{2}{\frac {d\theta _{1}}{dt}}=2{\frac {dA_{1}}{dt}}}$

이제 궤도의 반지름은 같지만 각도 변화에 상수 k가 곱해진 두 번째 입자를 생각해 보십시오.

${\displaystyle \theta _{2}(t)=k\theta _{1}(t)\,\!}$

두 번째 입자의 실제 속도는 첫 번째 입자의 실제 속도에 같은 인자 k를 곱한 것과 같습니다.

${\displaystyle h_{2}=2{\frac {dA_{2}}{dt}}=r^{2}{\frac {d\theta _{2}}{dt}}=kr^{2}{\frac {d\theta _{1}}{dt}}=2k{\frac {dA_{1}}{dt}}=kh_{1}}$

k는 상수이므로 두 번째 입자도 같은 시간에 같은 면적을 쓸어냅니다. 따라서 명제 2에 의해 두 번째 입자도 중심₂ 힘 F(r)에 의해 작용합니다. 이것이 주민발의안 43의 결론입니다.

발의안 44호

두 물체가 동일하게 움직일 수 있는 힘의 차이는, 하나는 고정된 상태에서, 다른 하나는 회전하는 궤도에서, 그들의 공통 고도의 세제곱과 반대로 변합니다.^[44]

원래 중심 힘 F₁(r)에서 F₂(r)의 크기를 찾기 위해 뉴턴은 기하학과 구심 가속도의 정의를 사용하여 차이 F₂(r) - F(r₁)를 계산했습니다. 그는 그의 프린키피아 제44호에서 차이가 반지름의 역제곱에 비례한다는 것을 보여주었고, 구체적으로 위에 주어진 공식에 의해 뉴턴은 두 개의 일정한 면적 속도인 h와₁ h로₂ 표기했습니다.

${\displaystyle F_{2}(r)-F_{1}(r)=m{\frac {h_{1}^{2}-h_{2}^{2}}{r^{3}}}}$

제안 45; 문제 31

원에 매우 가까이 접근하는 궤도에서 apside의 운동을 찾는 것.^[24]

이 제안에서 뉴턴은 거의 원형 궤도의 한계에서 공전 궤도 정리의 결과를 도출합니다. 이 근사는 일반적으로 행성 궤도와 달이 지구를 도는 궤도에 유효합니다. 이 근사는 또한 뉴턴이 역제곱과 역큐브 힘 법칙뿐만 아니라 매우 다양한 중심 힘 법칙을 고려할 수 있게 해줍니다.

현대적 도함수

뉴턴 정리의 현대적인 유도는 휘태커(1937)^[45]와 찬드라세카르(1995)에 의해 발표되었습니다.^[42] 가정에 의하면, 두 번째 각속도는 첫 번째 각속도보다 k배 빠릅니다.

${\displaystyle \omega_{2}={\frac {d\theta_{2}}{dt}}=k{\frac {d\theta_{1}}{dt}=k\omega_{1}}$

두 반지름이 시간에 따라 동일한 거동을 가지므로, 보존된 각운동량은 동일한 인자 k에 의해 연관됩니다.

${\displaystyle L_{2}=mr^{2}\omega _{2}=mr^{2}k\omega _{1}=kL_{1}\,\!}$

중심 퍼텐셜 V(r)에서 움직이는 질량 m의 입자의 반지름 r에 대한 운동 방정식은 라그랑주 방정식에 의해 주어집니다.

${\displaystyle m{\frac {d^{2}r}{dt^{2}}}-mr\omega ^{2}=m{\frac {d^{2}r}{dt^{2}}}-{\frac {L^{2}}{mr^{3}}}=F(r)}$

일반 공식을 두 궤도에 적용하면 방정식은 다음과 같습니다.

${\displaystyle m{\frac {d^{2}r}{dt^{2}}}=F_{1}(r)+{\frac {L_{1}^{2}}{mr^{3}}}=F_{2}(r)+{\frac {L_{2}^{2}}{mr^{3}}}=F_{2}(r)+{\frac {k^{2}L_{1}^{2}}{mr^{3}}}}$

양식에 다시 arranged할 수 있습니다.

${\displaystyle F_{2}(r)=F_{1}(r)+{\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)}$

두 반지름 힘에 관한 이 방정식은 정성적으로 다음과 같이 이해될 수 있습니다. 각속도의 차이(또는 이와 동등하게 각운동량)는 구심력 요건의 차이를 유발합니다. 이를 상쇄하려면 반경력을 역-큐브 힘으로 변경해야 합니다.

뉴턴의 정리는 중심력에 대해 정의되는 퍼텐셜 에너지로 동등하게 표현될 수 있습니다.

${\displaystyle F(r)=-{\frac {dV}{dr}}$

반지름 힘 방정식은 두 퍼텐셜 에너지로 나타낼 수 있습니다.

${\displaystyle -{\frac {dV_{2}}{dr}}=-{\frac {dV_{1}}{dr}}+{\frac {L_{1}^{2}}{mr^{3}}}\left(1-k^{2}\right)}$

거리 r에 대하여 적분하면, 각속도의 k배 변화는 임의의 주어진 퍼텐셜 에너지₁ V(r)에 역제곱 퍼텐셜 에너지를 더함으로써 발생한다고 뉴턴의 정리는 말합니다.

${\displaystyle V_{2}(r)=V_{1}(r)+{\frac {L_{1}^{2}}{2mr^{2}}}\left(1-k^{2}\right)}$

뉴턴의 원리에 의한 기하학적 증명

명제 44의 단순화된 기하학적 증명

뉴턴은 명제 6에 의해 문제가 해결되어야 한다고 말하지만, 그는 그것을 명시적으로 사용하지 않습니다. 다음에서는 단순화된 증명인 명제 6을 사용하여 결과가 어떻게 도출되는지 보여줍니다.

뉴턴의 상세한 증명은 그 뒤를 따르고, 마지막으로 잘 알려지지 않았기 때문에 명제 6이 추가됩니다.

제안 44는 제안 6을 사용하여 회전 궤도에 대한 결과를 증명합니다. 공국 제2절의 명제 6에 이어지는 명제에서 그는 이를 구체적인 곡선, 예를 들어 원뿔형 단면에 적용합니다. 제안 44의 경우, 고정점을 향하는 임의의 힘의 작용 하에, 이는 해당 회전 궤도를 생성하기 위해 모든 궤도에 적용됩니다.

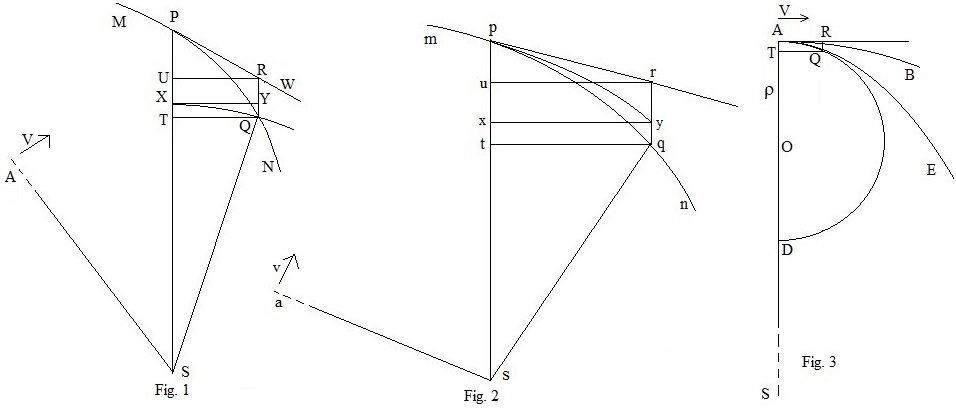
그림 1에서 MN은 그 궤도의 일부입니다. 점 P에서 몸은 이전과 마찬가지로 S를 향하는 힘의 작용 아래 Q로 이동합니다. 힘, F(SP)는 곡선의 각 점 P에서 정의됩니다.

그림 2에서 회전 궤도의 해당 부분은 s를 힘의 중심으로 하는 mn입니다. 처음에 정지 궤도에 있는 물체가 속도 V로 반지름에 대해 직각으로 출발한다고 가정합니다. 회전 궤도에 있는 물체도 직각으로 출발해야 하며 속도를 v로 가정해야 합니다. 그림 1의 경우 > ${\displaystyle v>$ V$}$이고 힘은 S를 향합니다. 인수는 < ${\displaystyle v< V}$인 경우에도 동일하게 적용됩니다 또한 힘이 중심에서 멀어질 수 있습니다.

SA를 정적 궤도의 초기 방향이라고 하고, SA를 회전 궤도의 초기 방향이라고 합니다. 일정 시간 후 각 궤도의 물체가 P와 p에 있으면 각도의 ${\displaystyle \frac{\mathrm{비율}}{}}$은 ${\displaystyle \frac{\mathrm{pASP}}{}}$ = ${\displaystyle \frac{\mathrm{ps}}{}}$ ${\displaystyle \frac{q}{}}$ ${\displaystyle \frac{\mathrm{PSQ}}{}}$= ${\displaystyle \frac{\mathrm{vV}}{}}$ ${\displaystyle {\frac {asp}}$입니다.$ASP}}={\frac {psq}{$$PSQ$}}$=${\$frac$${\displaystyle \frac{}{}}${v$}{$V}}; spASP $=$ psq PSQ $=$ vV {\displaystyle {\frac {asp}} 영역의 비율$ASP}}={\frac {psq}{$$PSQ$}}$=${\$frac$${\displaystyle }${v}{V}}; 그리고 반경 $$ $=$$sp$ ${\$$displaystyle$ SP $=$sp}, SQ $=$sq {\displaystyle SQ $=$sq}, SA $=$sa {\displaystyle SA $=$sa}입니다.

그림 2의 그림 pryx와 호는 그림 1의 그림 PRQT와 호 PQ로 비율 ${\displaystyle \frac{V}{}}$ ${\displaystyle {\frac {v}{V$에서 가로 방향으로 선형으로 확장되어 ${\displaystyle \mathrm{PU}}$ = ${\displaystyle \mathrm{pu}}$ ${\displaystyle PU$ = $pu$ ${\displaystyle U}$ T = ${\displaystyle u}$ ${\displaystyle UT$ =$ux$ 그리고 ${\displaystyle \mathrm{qt}}$ = ${\displaystyle v}$V $QT$ {\displaystyle qt = {\frac {v}{V}}}. 직선 qt와 QT는 각각 중심과 S 및 반지름 sq 및 SQ가 있는 원형 호여야 합니다. 제한에서는 비율이 ${\displaystyle \frac{\mathrm{직선}}{}}$이든 호든 vV ${\$이 됩니다$.$

한계에서 힘은 SP 및 sp와 평행하기 때문에 그림 1과 같은 힘이 몸에 작용하면 ry = RQ이기 때문에 몸은 y에 도달하게 됩니다. 수평 속도의 차이는 수직 거리에 영향을 미치지 않습니다. 뉴턴은 운동 법칙의 코롤러리 2를 언급하는데, 여기서 물체의 운동은 전체 힘에 의해 작용하는 반경 방향의 성분으로 분해되고, 반대쪽 성분은 아무런 힘에 의해 작용하지 않는 성분으로 분해됩니다.

그러나 y에서 중심까지의 거리 s는 이제 SQ보다 크므로 sq = SQ와 같이 몸체를 q로 이동하려면 추가적인 힘이 필요합니다. 여분의 힘은 yq로 표시되며 f는 RQ에 F가 있는 것과 마찬가지로 yq + yq에 비례합니다.

${\displaystyle \mathrm{RQ}}$ = ${\displaystyle \mathrm{SP}}$-$$PU${\displaystyle }$- ${\displaystyle \mathrm{ST}}$ $displaystyle$${\displaystyle }$$RQ$ = SP-PU-ST},${\displaystyle }$rq = sp - p -${\displaystyle }$st = RQ$$+ ST - st {\displaystyle${\displaystyle }$rq = sp - p - p -${\displaystyle }$st = RQ+$ST-st$

${\displaystyle \mathrm{차이}}$인${\displaystyle \mathrm{ST}}$ - st = ${\displaystyle y}$ ${\$displaystyle ST-st=yq}는 다음과 같습니다.

${\displaystyle ST^{2}=SQ^{2}-QT^{2}}$, ${\displaystyle st^{2}=sq^{2}-qt^{2}}$, so ${\displaystyle (ST-st)(ST+st)=qt^{2}-QT^{2}}$.

그리고 한계에서 QT와 qt가 0에 가까워질수록 ${\displaystyle \mathrm{ST}}$+ ${\displaystyle \mathrm{st}}$ ${\displaystyle ST+st}$는 ${\displaystyle \mathrm{SQ}}$+ ${\displaystyle \mathrm{sq}}$ ${\displaystyle SQ+sq}$ 또는$$ 2SP와 같아집니다$$.

$=$$T^{2}(v^{2}-V^{2})}{V^{2}}}}$.

따라서 ${\displaystyle \mathrm{rq}}$ = ${\displaystyle \mathrm{RQ}}$+ ${\displaystyle \frac{ST}{}}$ - $st$ = $RQ$+ Q T 2 (v 2 - V 2 ) 2 SP ∗ V 2 {\display rq = RQ+$ST-st=RQ+{\frac {Q$$T^{2}(v^{2}-V^{2})}{2$$SP*V^{2$

명제 6(그림 1 및 아래 참조)에서 힘은 ${\displaystyle \frac{k}{}}$ ∗ $SP$ ${\displaystyle \frac{{}^{}}{}}$ ∗ QT 2)${\displaystyle {\frac$ {k*QR}{(SP^{2}*$QT^{2$ (${\displaystyle \frac{{SP2}^{}}{}}$ $∗$ $)$ k${\displaystyle {\frac${(SP^{2}}*$QT^{2}}}{k$ 여기서 k는 일정한 $힘$ f${\displaystyle (s}$p) $=$ ${\displaystyle F(s}$p) + k(v 2 - V 2 ) 2초 p 3 $∗$ V 2 {\displaystyle f(sp) $=$ F(sp) + {\frac {k(v^{2}-V^{2}}{2sp^{3}*V^{2}}}.

그림 3에서 정적 곡선의 초기점 A에 SA에 수직인 접선 AR과 A에서 곡선에 딱 닿는 원 AQD를 그립니다. ρ을 그 원의 반지름으로 하시오. 각도 SAR은 직각이므로 원의 중심은 SA에 있습니다. 원의 속성에서 $Q$ ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$ = ${\displaystyle \mathrm{AT}}$(${\displaystyle 2}$ρ - AT) = R Q (2 ρ - R Q) {\displaystyle QT^{2} = AT(2\rho -AT) = RQ(2\rho - RQ)}이며, Q가 A에 가까워질수록 한계에서 이는 ρ = Q T 2 / 2 R Q {\displaystyle \rho = QT^{2}/2 RQ}가 됩니다.

따라서 $F{\displaystyle (\mathrm{SA})}$ = ${\displaystyle k\frac{(2}{}}$ρ ∗$$SA 2) {\displaystyle F(SA)={\frac {k}{(2\rho *SA^{2}}}}.

그리고 F(SA)가 주어지기 때문에 이것은 상수 k를 결정합니다. 그러나 뉴턴은 A에서의 힘이 c ${\displaystyle V^{}}$ ${\displaystyle {}^{}}$/ ${\displaystyle {SA}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle cV^{2}/SA^{2}}$의 형태가 되기를 원하며$,$ 여기서 c는 상수이므로 f (${\displaystyle s}$ p${\displaystyle )}$ = ${\displaystyle F}$(s ${\displaystyle p)}$+ c${\displaystyle \frac{{}^{}}{}}$ρ$$(v 2 - V 2) s p 3 {\displaystyle f(sp) = F(sp) + {\frac {c\rho(v^{2}-V^{2}}} {sp^{3}}, 여기서 $c$ = F $(SA$) ∗ SA 2 V 2 {\displaystyle c = {\frac {F(SA)*SA^{2}}{V^{2}}}.

위의 f(sp)에 대한 표현은 명제 44의 코롤러리 4에 나오는 뉴턴의 표현과 다른 문자를 사용한다는 점을 제외하고는 같습니다. 그는 ${\displaystyle \frac{\mathrm{GF}}{}}$ = ${\displaystyle \frac{v}{}}$ ${\displaystyle V}$ ${\$displaystyle {\frac {G}{F}}={\frac {v}{V}}}(여기서 G와 F는 각각 v와 V와 반드시 동일할 필요는 없습니다)라고 쓰고, "c"에 해당하는 상수에는 문자 "V"를, 함수 F(sp)에는 문자 "X"를 사용합니다.

위의 기하학적 증명은 정지 궤도에 대해 궤도를 회전시키기 위해 추가적인 힘이 어디에서 발생하는지를 매우 명확하게 보여줍니다.

뉴턴의 명제 증명 44

뉴턴의 증명은 위의 증명의 단순성으로 볼 때 복잡합니다. 예를 들어, 그의 증명은 다음 문장에서 알 수 있듯이 약간의 해독을 필요로 합니다.

"따라서, 중심 C와 어떤 반지름 CP 또는 Cp를 갖는 원형 섹터가 중심으로 그려지는 반지름에 의해 고정된 궤도를 회전하는 몸체 P가 어느 때라도 묘사한 총 면적 VPC와 동일하다고 기술된다면, 움직이지 않는 궤도에 있는 물체 P와 이동 궤도에 있는 물체 P가 회전하는 힘의 차이는 중심에 그려진 반지름을 통해 물체가 그 영역을² G² - F ~ F로² 묘사할 때 균일하게 그 영역을 묘사할 수 있을 것입니다."

그는 처음에 무한소$$τ {\displaystyle$$\tau}을(를) 고정된 것으로 간주하고 영역 SPQ와 spq는 각각 V와 v에 비례합니다${\displaystyle .}$ ${\displaystyle \mathrm{따라서}}$ ${\displaystyle \mathrm{QT}}$∗ SP ∝$$V τ ${\$displaystyle QT*SP\propto V\tau} 및 qt ∗ sp ∝ v τ {\displaystyle qt*sp\propto v\tau}를 각 점 P와 p에서, 그리고 $y$ ${\displaystyle q}$ = $t$ 2 - Q T 22 sp ∝ 1 sp 3 {\displaystyle yq={\frac {qt^{2}-QT^{2}}{2sp}\propto {\frac {1}{sp^{3}}} 이므로 추가 힘은 반지름의 세제곱과 반비례합니다.

그림 1에서 XQ는 중심 S와 반지름 SQ가 X에서 SP를 만나는 원형 호입니다. 수직 XY는 Y에서 RQ를 충족하고 ${\displaystyle \mathrm{YQ}}$ = ${\displaystyle \frac{Q^{}}{}}$ T ${\displaystyle \frac{\mathrm{22}}{}}$ SP${\$displaystyle YQ = {\frac ${Q$$T^{2}}{2$$SP$

ϕ${\displaystyle }$($SQ)$ {\displaystyle \phi (SQ)}가 Q에서 정적 궤도에서 물체의 횡방향 속도와 같은 속도일 경우, 물체를 반지름 SQ의 원을 그리며 움직이는 데 필요한 힘이라고 가정합니다.

${\displaystyle {\frac {f(sp)-F(sp)}{\phi (sp)}}={\frac {yq}{YQ}}={\frac {(qt^{2}-QT^{2})}{QT^{2}}}={\frac {(v^{2}-V^{2})}{V^{2}}}}$

모든 지점에서 P, 특히 apside에서 A:

${\displaystyle \frac{f}{}}$(${\displaystyle \frac{\mathrm{SA})}{}}$- ${\displaystyle \frac{F}{}}$(${\displaystyle \frac{\mathrm{SA})}{}}$ (SA) ${\displaystyle =}$ (${\displaystyle \frac{v{}^{}}{}}$2 - ${\displaystyle \frac{}{}}$ ) V$2$ {\displaystyle {\frac {f(SA)-F(SA)}{\phi${\displaystyle \frac{(}{}}$SA)}} = {\frac {(v^{2}-V^{2}}} {V^{2}}}.

그러나 그림 3에서 물체가 원을 따르는데 필요한 정적 곡선인 AE를 따르도록 하는 힘의 비율과 반지름이 SA인 AB는 둘 다 같은 속도로 움직이기 때문에 곡률 반경의 비율과 반대입니다. V, SA에 수직: $F{\displaystyle \frac{(\mathrm{SA})}{}}$ϕ(SA) = SA ρ${\displaystyle${\$frac$ {F(SA)}{\phi(SA)}} ={\frac {SA}{\rho }}. 증명의 첫 부분부터, ${\displaystyle f(sp)-F(sp)={\frac {(f(sa)-F(sa))sa^{3}}{sp^{3}}}={\frac {\rho F(sa)sa^{2}(v^{2}-V^{2})}{V^{2}sp^{3}}}}$.

뉴턴의 식을 F(SA)에 대입하면 앞서 얻은 결과를 얻을 수 있습니다.

뉴턴의 명제 증명 45

"원에 접근하는 궤도에서 apside의 운동을 찾기 위해."

제안 44는 이 제안을 증명하기 위해 명시적으로 고안되었습니다. 뉴턴은 $형태$ f${\displaystyle (\mathrm{sp}}$) =${\displaystyle }$γ ∗ sp - 3 {\display f(sp)=\gamma *sp^{n-3}}의 힘에 의해 끌리는 거의 원형 궤도에 있는 물체의 운동을 조사하려고 합니다.

제안 44에 따르면, 그는 역입방체 힘의 추가에 의해 회전하는 초점 중 하나로 향하는 역제곱 힘 F(SP)를 갖는 타원에 의해 정적 곡선의 근사치를 나타냅니다.

정적 타원의 경우 힘이 SP 제곱에 반비례하여 $F{\displaystyle (\mathrm{SP})}$ = ${\displaystyle c}$ V ${\displaystyle \frac{2^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\$displaystyle F(SP) = {\frac ${cV^{2$}}{$SP^{2$ c는 F${\displaystyle (\mathrm{SA})}$ $=$ ${\displaystyle c}$ ${\displaystyle \frac{{}^{}}{}}$ 2 ${\displaystyle \frac{{}^{}}{}}$ {\displaystyle F(SA) $=$ {\frac ${cV^{2$}}{$SA^{2$

정지 궤도에 있는 물체를 위쪽 변에서 A로 시작한 상태에서 180도 각도를 통해 이동한 후 S와 가장 가까운 지점인 아래쪽 변에 도달하게 됩니다. 뉴턴은 해당 회전 궤도를 한 변에서 시작하여 한 점에 대해 a로 시작하며, 아래 변은 각도만큼 이동하고 α$,$ ${\displaystyle \frac{\mathrm{여기}}{}}$서 ${\displaystyle \frac{(\mathrm{180}}{}}$ ${\displaystyle \frac{+}{}}$ α) ${\displaystyle \frac{\mathrm{180}}{}}$= {\displaystyle {\frac {(180+\alpha)}{180}} = {\frac {v}{V}}.

A에서의 초기 속도 V는 몸이 원을 그리며 움직이는 데 필요한 속도보다 약간 작아야 합니다. 그러면 ρ는 SA 또는 SA와 동일한 것으로 간주할 수 있습니다. 문제는 n의 값에서 v를 결정하여 α를 찾거나, α를 주어 n을 찾는 것입니다.

${\displaystyle f(sp)=F(sp)+{\frac {c\rho (v^{2}-V^{2})}{sp^{3}}}={\frac {c(sp*V^{2}+sa(v^{2}-V^{2}))}{sp^{3}}}$

${\displaystyle \mathrm{sp}}$ = ${\displaystyle \mathrm{sa}}$- X {\displaystyle sp = sa-X}을(를) 둡니다.

${\displaystyle f(sp)}$ = ${\displaystyle c}$(s ∗ av 2 - XV 2) sp 3 {\displaystyle f${\displaystyle (}$sp)={\frac {c(s*av^{2}-XV^{2}}{sp^{3}}}.

그런 다음 "계열을 수렴하는 방법으로": $f{\displaystyle }$(${\displaystyle s}$ ${\displaystyle p}$) =${\displaystyle \frac{}{}}$γ ∗${\displaystyle \frac{}{}}$s p${\displaystyle \frac{}{}}$n s p ${\displaystyle \frac{3}{}}$ = γ (sa - X ) n s p 3 = γ ∗ s - 1 (sa - n X ) sp 3 {\displaystyle f(sp)={\frac {\gamma *sp^{n}}{sp^{3}}={\frac {\gamma (sa-X)^{n}}{sp^{3}}={\frac {\gamma *sa^{n-1}(sa-nX)}{sp^{3}}}+ X 이상의 항 궤도가 거의 원형이므로 X는 sa에 비해 작기 때문에 무시할 수 있습니다.

f(sp)에 대한 두 식을 비교하면, ${\displaystyle f(sp)={\frac {\gamma *sa^{n-1}(sa-nX)}{sp^{3}}}={\frac {c(sa*v^{2}-XV^{2})}{sp^{3}}}}$ it follows that ${\displaystyle {\frac {v}{V}}={\frac$${1}{n^{1/2$}}$=${\$frac {(180+\alpha )}{180$

또한 f${\displaystyle (\mathrm{sp})}$ = ${\displaystyle \frac{{}^{}}{}}$ 2$$∗ sp - 3초 n - 1 {\displaystyle f(sp)={\frac {cv^{2}*sp^{n-3}}{sa^{n-1}}}.

a에서의 초기 힘의 $비율$은 f${\displaystyle \frac{(\mathrm{sa})}{}}$ ${\displaystyle \frac{(\mathrm{sa})}{}}$ = ${\displaystyle 1}$ ${\$displaystyle {\frac {f(sa)}{F(sa)}} = {\frac {1}{n}}에 의해 주어집니다.

제안서 44의 증명을 위한 제안서 6, 위

그림 1에서 물체는 (구심) 힘에 의해 작용하는 특정 곡선 MN을 따라 고정점 S를 향해 이동하고 있습니다. 힘은 S로부터의 점의 거리에만 의존합니다. 이 제안의 목적은 힘이 반지름인 SP에 따라 어떻게 변하는지를 결정하는 것입니다. 이 방법은 힘이 원심력인 경우에도 동일하게 적용됩니다.

τ$${\$displaystyle$\tau$\}$라는 작은 시간 안에 본체가 P에서 가까운 지점 Q로 이동합니다. R에서 접선을 만나는 SP에 평행하게 QR을 그리고 T에서 만나는 SP에 수직으로 QT를 그립니다.

만약 힘이 없다면, 그것은 P에서 접선을 따라 움직였을 것이고, P에서 속도가 R인 점에 도달했을 것입니다. P에서 Q로 움직이는 물체에 작용하는 힘이 크기가 일정하고 방향 SP에 평행하다면, 호 PQ는 PR을 접선으로 하는 포물선이며 QR은 일정한 힘과 시간의 제곱인$$τ${\displaystyle$tau}에 비례합니다.

반대로 R에 도달하는 대신 몸체가 Q로 편향된 다음 크기로 SP에 평행한 일정한 힘으로 편향되었습니다. ${\displaystyle \frac{F^{}}{}}$ $QR$τ 2${\displaystyle F\propto {\frac {$QR}{\tau ^{2}}}는 R이 아닌 Q에 도달하게 했을 것입니다.

그러나 S에서 호 PQ의 점으로 향하는 반지름의 방향과 S로 향하는 힘의 크기는 PQ를 따라 변하므로 위의 관계는 P에서의 정확한 힘을 제공하지는 않을 것입니다. Q가 P에 충분히 가깝다면 힘의 방향은 PQ를 따라 SP와 거의 평행할 것이고 힘이 거의 변하지 않는다면 PQ는 위와 같은 힘을 가진 포물선 호로 근사된다고 가정할 수 있습니다. QR 및$$τ${\displaystyle$\tau}.

τ$${\$displaystyle$\tau} 시간은 섹터 SPQ의 면적에 비례합니다. 이것은 케플러의 제2법칙입니다. 증명은 명제 1, 1권, 공국에서 입증됩니다. 원호 PQ는 직선으로 근사할 수 있으므로 섹터 SPQ의 면적과 삼각형 SPQ의 면적을 같게 취할 수 있으므로

$∝$$QT^{2$ 여기서 k는 상수입니다.

다시 말하지만, 이것은 유한 길이 PQ에 대해서는 정확하지 않습니다. 위 식의 극한이 SP의 함수로 존재하는 경우 PQ가 0에 가까워지면 힘 법칙이 얻어집니다.

실제로 시간$$τ {\displaystyle$$\tau$\}$에서 힘이 없는 물체는 R보다 P에서 더 멀리 떨어진 점 W에 도달했을 것입니다. 그러나 한계에서 QW는 SP와 평행하게 됩니다. 뉴턴의 증명에서 점 W는 무시됩니다.

또한 Newton은 QR을 중심에 P가 있고 길이가 QP의 두 배인 호의 역방향 사인으로 설명합니다. 이것은 그가 도표에서 가지고 있는 QR(그림 1)과 완전히 같은 것은 아니지만, 제한적으로 그들은 동등하게 됩니다.

주의:

이 명제는 일정한 가속도의 작용 하에서 포물선 궤적을 따라가는 물체에 대한 갈릴레오의 분석에 기초합니다. 명제 10에서, 그는 그것을 갈릴레오의 정리라고 설명하고, 프린시페아에서 그것과 관련하여 갈릴레오를 몇 번 더 언급합니다. 케플러의 제2법칙과 결합하면 간단하고 우아한 방법을 얻을 수 있습니다.

그림 1의 MN이 타원의 일부이고 S가 초점 중 하나였던 역사적으로 매우 중요한 경우, 뉴턴은 명제 11에서 $한계{\displaystyle }$ ${\displaystyle \mathrm{QR}}$/ ${\displaystyle {QT\mathrm{}}^{}}$ 2 ${\$$T^{2}}$는 곡선의 각 점에서 일정하여$$ 고정점 S를 향하는 신체에 작용하는 힘은 거리 SP의 제곱에 반비례하여 변했습니다.

중심이 있는 타원 외에도 뉴턴은 쌍곡선(명제 12), 포물선(명제 13), 타원의 중심에 힘의 중심이 있는 타원(명제 10), 등각 나선(명제 9), 힘의 중심이 중심과 일치하지 않는 원에도 명제 6을 적용했습니다. 그리고 심지어 둘레(안 7)에서도.

참고 항목

• 케플러 문제
• 라플라스-룽지-렌츠 벡터
• 일반상대성이론의 양체문제
• 타원에 관한 뉴턴의 정리

참고문헌

서지학

• Newton I (1999) [1726]. The Principia: Mathematical Principles of Natural Philosophy. Translated by I. Bernard Cohen; Anne Whitman; Julia Budenz (3rd ed.). Berkeley, CA: University of California Press. pp. 147–148, 246–264, 534–545. ISBN 978-0-520-08816-0.
• Chandrasekhar S (1995), Newton's Principia for the Common Reader, Oxford University Press, pp. 183–200, ISBN 978-0-19-852675-9
• Pars, L.A. (1965). A Treatise on Analytical Dynamics. John Wiley and Sons. p. 56. ISBN 978-0-918024-07-7. LCCN 64024556.
• Whittaker ET (1937). A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies (4th ed.). New York: Dover Publications. p. 83. ISBN 978-0-521-35883-5.
• Routh EJ (1960). A Treatise on Dynamics of a Particle (reprint of 1898 ed.). New York: Dover Publications. pp. 230–233 (sections §356–359). ISBN 978-0-548-96521-4.
• Rouse Ball WW (1893). An Essay on Newton's "Principia". Macmillan and Co. (reprint, Merchant Books). pp. 84–85. ISBN 978-1-60386-012-3.
• Heilbron, J. (2005), The Oxford Guide to the History of Physics and Astronomy, Oxford University Press, USA, Bibcode:2005oghp.book.....H, ISBN 978-0-19-517198-3
• Fitzpartrick, Richard (2012), An Introduction to Celestial Mechanics, Cambridge University Press, ISBN 978-1-107-02381-9
• Lambourne, Robert (2010), Relativity, Gravitation and Cosmology, Cambridge University Press, ISBN 978-0-521-13138-4
• Grossman, Nathaniel (1996), The Sheer Joy of Celestial Mechanics, Springer Science & Business Media, ISBN 978-0-8176-3832-0
• Shikin, Eugene (1995), Handbook and Atlas of Curves, CRC Press, ISBN 978-0-8493-8963-4
• Lawrence, J. Dennis (1972), A Catalog of Special Plane Curves, New York: Dover, ISBN 0486602885
• Weisstein, Eric (2002), CRC Concise Encyclopedia of Mathematics, Second Edition, CRC Press, ISBN 978-1-4200-3522-3

더보기

• Bertrand J (1873). "Théorème relatif au mouvement d'un point attiré vers un centre fixe". Comptes rendus hebdomadaires des séances de l'Académie des Sciences. xxvii/10: 849–853. (1873년 10월 20일)
• Cohen IB (1999). "A Guide to Newton's Principia". The Principia: Mathematical Principles of Natural Philosophy. Berkeley, CA: University of California Press. pp. 147–148, 246–252. ISBN 978-0-520-08816-0.
• Cook A (1988). The Motion of the Moon. Bristol: Adam Hilger. ISBN 0-85274-348-3.
• D’Eliseo, MM (2007). "The first-order orbital equation". American Journal of Physics. 75 (4): 352–355. Bibcode:2007AmJPh..75..352D. doi:10.1119/1.2432126.
• Guicciardini, Niccolò (1999). Reading the Principia: The Debate on Newton's Mathematical Methods for Natural Philosophy from 1687 to 1736. Cambridge University Press. ISBN 978-0-521-54403-0.
• Newton I (1966). Principia Vol. I The Motion of Bodies (based on Newton's 2nd edition (1713); translated by Andrew Motte (1729) and revised by Florian Cajori (1934) ed.). Berkeley, CA: University of California Press. pp. 135–147 (Section IX of Book I). ISBN 978-0-520-00928-8. 뉴턴의 프린시피아의 이전(2차) 판본의 대체 번역.
• Smith GE (1999). "Newton and the Problem of the Moon's Motion". The Principia: Mathematical Principles of Natural Philosophy. Berkeley, CA: University of California Press. pp. 252–257. ISBN 978-0-520-08816-0.
• Smith GE (1999). "Motion of the Lunar Apsis". The Principia: Mathematical Principles of Natural Philosophy. Berkeley, CA: University of California Press. pp. 257–264. ISBN 978-0-520-08816-0.
• Spivak, Michael (1994). "Planetary Motion". Calculus (3rd ed.). Publish or Perish. ISBN 0-914098-89-6.

외부 링크

• Scholarpedia의 Alain Chenciner에 의해 논의된 3체 문제