위상 큐비트
Phase qubit양자 컴퓨팅, 특히 초전도 양자 컴퓨팅에서 위상 큐비트는 초전도체-절연체-슈퍼컨덕터(SIS) 조셉슨 [1]접점에 기초한 초전도 소자로, 양자 비트 또는 큐비트로 [2]작동하도록 설계됩니다.
위상 큐비트는 플럭스 큐비트 및 전하 큐비트와는 밀접하게 관련되어 있지만, 초전도 소자에 의해 구현되는 양자 비트이기도 합니다.세 가지 주요 차이점은 조지프슨 에너지 대 충전[3] 에너지(Coper 쌍 하나가 회로의 총 캐패시턴스를 충전하는 데 필요한 에너지)의 비율입니다.
- 위상 큐비트의 경우 이 비율은 10 정도이며6, 이는 접점을 통과하는 거시적 바이어스 전류를 허용한다.
- 플럭스 큐비트의 경우 메소스코프 초전류(일반적으로 약 300nA[4])를 허용하는 약 10입니다.
- 충전 큐비트의 경우 1보다 작기 때문에 소수의 Cooper 쌍만이 터널을 통해 Cooper-pair 박스를 충전할 수 있습니다.그러나 트랜스몬은 션트 캐패시턴스가 크기 때문에 충전 에너지가 매우 낮기 때문에 이 비율은 10~[5]100 정도 됩니다.
서론
위상 큐비트는 전류 바이어스가 0이 아닌 전압 상태에서 작동하는 전류 바이어스 조지프슨 접합부입니다.
조지프슨 접합부는 두께 약 1nm의 매우 얇은 절연 장벽으로 분리된 두 개의 초전도 금속 조각으로 만들어진 터널 [6]접합부입니다.장벽은 전자, 또는 초전도 상태에 있는 쿠퍼 쌍 전자가 장벽을 상당한 속도로 통과할 수 있을 정도로 얇습니다.조지프슨 접합부를 구성하는 각 초전도체는 초전도체에 [7]대한 긴츠부르크-란다우 이론에서 설명한 것처럼 거시적 파동 함수에 의해 설명됩니다.두 초전도 파동함수의 복잡한 위상 차이는 조셉슨 접합부의 가장 중요한 동적 변수이며 위상차 \ 또는 단순히 "상"이라고 불립니다.
SIS 접합을 설명하는 주요 방정식
조지프슨[1] 방정식은 터널 접점을 통과하는 초전도 전류(일반적으로 슈퍼 전류라고 함) delta)와 위상차(\를 관련짓습니다.
- (조셉슨 전류-상 관계)
서 은 터널 접합부의 임계 전류로 접합부의 터널 장벽 면적과 두께 및 장벽 양쪽에 있는 초전도체의 특성에 의해 결정됩니다.장벽 양쪽에 동일한 초전도체가 있는 접합부의 경우 임계 전류는 암베가오카-바라토프 공식에 따라 초전도 간격 및 터널 접합부의 정상 Rnn})과 관련이 있다.
- 0 2 R {_ { 0 } = {\ \ Delta } { 2 _ { n } ( Ambegaokar - Baratoff formula )
Gor'kov 위상 진화[1] 방정식은 전압 V의 선형 함수로서 위상 변화율(위상의 "속도")을 다음과 같이 제공합니다.
- d d { V = frac {} { { \ { d\ { } ( Gor'kov - Josephson evolution evolution equation equation equation))))))))))))))))) equation equation )
이 방정식은 BCS 파동 함수의 위상에 대한 슈뢰딩거 방정식의 일반화입니다.Gor'kov는 [8]1958년에 일반화를 실시했다.
McCumber-Stewart 모델
대체 및 직류 조셉슨 관계는 조셉슨 접합 자체의 동작을 제어합니다.얇은 터널 장벽으로 분리된 두 개의 초전도 금속 판인 조지프슨 접합부의 형상은 평행판 캐패시터이므로 조지프슨 소자 외에 이 소자는 평행 C(\ C를 포함합니다.외부 회로는 보통 Josephson 소자와 병렬로 R R로 모델링됩니다.3개의 병렬 회로 소자 세트는 외부 전류 I I에 의해 바이어스되므로 전류 바이어스된 조지프슨 [9]접점이 됩니다.회로 방정식을 풀면 위상에 대한 단일 동적 방정식이 생성됩니다.
- d d + 2 d t= - I 、 { \ { } { 2 e } , { \ { { + { \ } { \ frac { 2 } { dt } } \ 、 {
The terms on the left side are identical to those of a particle with coordinate (location) , with mass proportional to the capacitance , and with friction inversely proportional to the resistance . The particle moves in a conservative force field given by the ter오른쪽의 m은 입자가 퍼텐셜 U U와 상호작용하는 것에 대응합니다.
- ( ) 2( - - ){ \ } { 2 e } \ left ( - _ } \ \ , \ )
이것은 "세탁기전위"[9]입니다.는 전체적인 선형 의존성이 있기 때문입니다.- I { \ - I , \ 세탁기 에 의해 됩니다 I cos { \ - _ }, \ cos \
제로 전압 상태는 위상 입자에 의해 표시되는 두 가지 뚜렷한 동적 동작 중 하나를 나타내며, 입자가 세탁기 전위의 로컬 최소값 중 하나에 갇힌 경우에 해당합니다.이러한 최소값은 바이어스 I < 0\ \ I \ < I { } 、 즉 임계 전류 미만인 전류에 대해 존재합니다.위상 입자가 최소로 갇히면 평균 속도가 0이므로 평균 전압이 0이 됩니다.조지프슨 접합부는 I I_까지의 를 아무런 전압 없이 통과시킵니다. 이는 조지프슨 접합부의 전류-전압 특성에 해당하는 초전도 분기에 해당합니다.
전압 상태는 조지프슨 접합부에 의해 표시되는 다른 동적 동작으로, 0이 아닌 평균 속도, 즉 0이 아닌 전압으로 전위의 기울기를 자유로이 내려가는 위상 입자에 해당합니다.이 동작은 항상 임계 전류보다 높은 : I> I 0 \0에서 발생하며, 저항이 전류보다 약간 낮은 전류에서도 R R이 발생합니다.이 상태는 조지프슨 접합 전류-전압 특성의 전압 분기에 해당합니다.큰 저항 접점의 경우 임계 전류보다 낮은 전류 범위에서 영전압 및 전압 분기가 겹치므로 장치 동작이 이력적입니다.
비선형 인덕터
제로 전압 상태에서 조지프슨 접합부의 동작을 이해하는 또 다른 방법은 SIS 터널 접합부를 비선형 [10]인덕터로 간주하는 것입니다.위상이 최소값 중 하나에 갇히면 위상값은 최소값의 위상값의 작은 범위로 제한됩니다. 값을 0 _이라고 합니다.접점을 통과하는 전류는 다음과 같이 이 위상 값과 관련이 있습니다.
- _
최소 0({displaystyle _접점을 제로 전압 상태로 유지할 수 있을 정도로 작음)의 위상에서의 작은 변화 \를 고려할 경우 전류는 다음과 같이 변화합니다.
- 。
위상에서의 이러한 변화는 교류 조셉슨 관계를 통해 전압을 발생시킵니다.
이 마지막 관계는 인덕턴스를 가진 인덕터에 대한 정의 방정식입니다.
- _
이 인덕턴스는 세탁기 전위의 최소 위상 0 _의 값에 따라 달라지므로 인덕턴스 값은 바이어스 I I를 변경하여 제어할 수 있습니다. 바이어스 전류가 제로일 경우 인덕턴스는 최소값에 도달합니다.
바이어스 전류가 증가함에 따라 인덕턴스가 증가합니다.바이어스 전류가 임계 0에 매우 가까운 경우(단, 위 dc Josephson 관계에서 볼 수 있듯이 위상 0 _ 값은 / 에 매우 가깝습니다.즉 인덕턴스 L({L})이 매우 커져 임계 0})에 하면 분산됩니다.
비선형 인덕터는 바이어스 전류 변화에 대한 조지프슨 접합부의 반응을 나타냅니다.장치 지오메트리의 병렬 캐패시턴스를 인덕터와 병렬로 포함하면 공진 주파수와 함께 LC) 공진기를 형성합니다.
- _ C
접합부의 플라즈마 주파수라고 알려져 있습니다.이는 세탁기 전위의 최소값 중 하나에 있는 위상 입자의 발진 주파수에 해당합니다.
임계 전류에 매우 가까운 바이어스 전류의 경우, 세탁기 최소의 위상 값은 다음과 같습니다.
- - ( / I ) 2\ \ _ { 0 } ={ 1 - ( / _ { 0}}、
플라즈마 주파수는
- C4
바이어스 전류가 임계 전류에 근접함에 따라 플라즈마 주파수가 0에 근접함을 명확히 보여준다.
제로 전압 상태에서 전류 바이어스 조지프슨 접합부의 단순한 조정성은 위상 큐비트가 다른 몇 가지 큐비트 구현에 비해 갖는 주요 장점 중 하나이지만, 전류의 변동으로 인해 플라즈마 주파수의 변동이 발생하여 양자 상태의 소멸을 야기하기 때문에 이 장치의 성능도 제한합니다.s.
정량화된 에너지 수준
The phase qubit is operated in the zero-voltage state, with .1K(희석냉장고로 알려진 극저온 시스템을 사용하여 달성 가능)보다 훨씬 낮은 온도에서 충분히 높은 저항과 작은 정전용량 조셉슨 접합을 가진 양자 에너지 수준은 세탁기 전위의 국소 최소값으로 검출될 수 있습니다.이들은 접점을 바이어스하는 I I에 약한 마이크로파 신호가 추가되는 마이크로파 분광법을 사용하여 처음 검출되었다.접점 전체의 전압을 모니터링하여 제로 전압 상태에서 전압 상태로의 전환을 측정했습니다.특정 주파수에서 명확한 공명이 관찰되었으며, 이는 세탁기 전위의 국소 최소값에 대한 슈뢰딩거[12] 방정식을 풀어서 얻은 양자 전이 에너지와 잘 일치했다.일반적으로 플라즈마 주파수 p {\ _를 중심으로 단일 공진만 예상된다. 양자역학적으로 세탁기 전위의 전위는 에너지 01 µ p{}에서 가장 낮은 (접지 상태에서 첫 번째 들뜬 상태로) 전이를 통해 여러 양자화된 에너지 레벨을 수용할 수 있다. \ _ 그러나 에너지가 최소로 증가할수록 공진 주파수가 떨어지는 트랩 전위의 비조화 특성 때문에 높은 에너지 전환(1~2차 들뜸 상태, 2~3차 들뜸 상태)은 이보다 약간 낮게 이동했다.이러한 방식으로 여러 개의 이산적인 수준을 관찰하는 것은 초전도 장치가 고전적인 것이 아니라 양자 기계적으로 작동하고 있다는 매우 강력한 증거입니다.
위상 큐비트는 로컬 최소값에서 가장 낮은2개의 에너지 레벨을 사용합니다.그라운드 g { g \ 는 큐비트의 "제로 상태"이고 첫 번째 들뜸 e { \ e \ }는 "하나의 상태"입니다.세탁기 전위의 기울기는 바이어스 I I에 의해 설정되며, 이 전류의 변화에 따라 세탁기 전위가 변경되어 로컬 최소값의 모양이 바뀝니다(따라서 위에서 설명한 것처럼 비선형 인덕턴스 값이 변경됩니다).이것은 지면과 첫 번째 들뜬 상태 사이의 에너지 차이를 변화시킨다.따라서 위상 큐비트는 조정 가능한 에너지 분할을 가진다.
레퍼런스
- ^ a b c Barone, Antonio; Paterno, Gianfranco (1981). Physics and Applications of the Josephson Effect. New York: Wiley.
- ^ Nielsen, Michael; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press.
- ^ You, J. Q.; Nori, Franco (2007-01-12). "Superconducting Circuits and Quantum Information". Physics Today. 58 (11): 42. arXiv:quant-ph/0601121. doi:10.1063/1.2155757. ISSN 0031-9228. S2CID 10969948.
- ^ 델프트 대학 - Flux Qubit 웹 사이트 2008-03-01 아카이브에 보관.오늘
- ^ Schreier, J. A.; Houck, A. A.; Koch, Jens; Schuster, D. I.; Johnson, B. R.; Chow, J. M.; Gambetta, J. M.; Majer, J.; Frunzio, L.; Devoret, M. H.; Girvin, S. M. (2008-05-12). "Suppressing charge noise decoherence in superconducting charge qubits". Physical Review B. 77 (18): 180502. arXiv:0712.3581. Bibcode:2008PhRvB..77r0502S. doi:10.1103/PhysRevB.77.180502. S2CID 119181860.
- ^ a b van Duzer, Theodore; Turner, Charles (1999). Principles of Superconductive Devices and Circuits, 2nd ed. Upper Saddle River NJ: Prentice-Hall.
- ^ Tinkham, Michael; Paterno, Gianfranco (1996). Introduction to Superconductivity. New York: McGraw-Hill.
- ^ L. P. Gor'kov (1958). "On the energy spectrum of superconductors". Sov. Phys. JETP. 7 (3): 505.
- ^ a b Likharev, Konstantin (1986). Dynamics of Josephson Junctions and Circuits. New York: Gordon and Breach.
- ^ Devoret, Michel; Martinis, John (2004). "Superconducting Qubits". In Esteve, Daniel; Raimond, J.-M.; Dalibard, J. (eds.). Quantum Entanglement and Information Processing. Elsevier. ISBN 0-444-51728-6.
- ^ J. M. Martinis; M. Devoret; J. Clarke (1985). "Energy-level quantization in the zero-voltage state of a current-biased Josephson junction". Phys. Rev. Lett. 55 (15): 1543–1546. Bibcode:1985PhRvL..55.1543M. doi:10.1103/PhysRevLett.55.1543. PMID 10031852.
- ^ Griffiths, David J. (2004). Introduction to Quantum Mechanics, 2nd ed. New York: Benjamin Cummings. ISBN 0-13-111892-7.



 터널 접합부의 임계 전류로 접합부의 터널 장벽 면적과 두께 및 장벽 양쪽에 있는 초전도체의 특성에 의해 결정됩니다.장벽 양쪽에 동일한 초전도체가 있는 접합부의 경우 임계 전류는 암베가오카-바라토프 공식에 따라 초전도 간격
터널 접합부의 임계 전류로 접합부의 터널 장벽 면적과 두께 및 장벽 양쪽에 있는 초전도체의 특성에 의해 결정됩니다.장벽 양쪽에 동일한 초전도체가 있는 접합부의 경우 임계 전류는 암베가오카-바라토프 공식에 따라 초전도 간격


 선형 함수로서 위상 변화율(위상의 "속도")을 다음과 같이 제공합니다.
선형 함수로서 위상 변화율(위상의 "속도")을 다음과 같이 제공합니다.

 모델링됩니다.3개의 병렬 회로 소자 세트는 외부 전류
모델링됩니다.3개의 병렬 회로 소자 세트는 외부 전류  상호작용하는 것에 대응합니다.
상호작용하는 것에 대응합니다.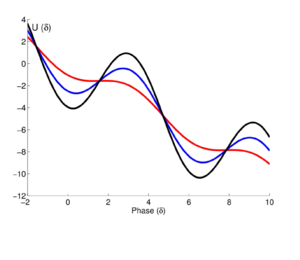







 고려할 경우 전류는 다음과 같이 변화합니다.
고려할 경우 전류는 다음과 같이 변화합니다.








![{\displaystyle \omega _{p}\approx {\sqrt {\frac {2eI_{0}}{\hbar C}}}\left[1-(I/I_{0})^{2}\right]^{1/4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aa832cf0999ca31df60cf2749b4121c996041ae)


 큐비트의 "제로 상태"이고 첫 번째 들뜸
큐비트의 "제로 상태"이고 첫 번째 들뜸 




