초전도 양자 컴퓨팅

초전도 양자 컴퓨팅(Superconducting Quantum Computing)은 초전도 큐비트를 인공 원자로 사용하여 초전도 전자 회로를 구현하는 고체 양자 컴퓨팅의 한 분야입니다.초전도 큐비트의 경우, 두 논리 상태는 각각 g ⟩ $|g\rangle {\text{ and }}|e\rangle$ $|g\rangle {\text{ and }}|e\rangle$ ⟩ $g\rangle {\text{ and }} e\rangle$ 로 표시되는 접지 상태 및 여기 상태입니다.초전도 양자 컴퓨팅 연구는 구글,^[2] IBM,^[3] IMEC,^[4] BBN 테크놀로지스,^[5] 리게티,^[6] 인텔 등의 기업에서 수행하고 있습니다.^[7]최근에 개발된 많은 QPU(양자 처리 장치 또는 양자 칩)는 초전도 구조를 사용합니다.

2016년^[update] 5월 현재, 1D 어레이에서는 최대 9개의 완전히 제어 가능한 큐비트가,^[8] 2D 아키텍처에서는 최대 16개의 큐비트가 시연됩니다.^[3]2019년 10월, 마르티니스 그룹은 구글과 협력하여 53개의 초전도 큐비트로 구성된 칩을 사용하여 새로운 양자 우월성을 보여주는 기사를 발표했습니다.^[9]

배경

고전적인 계산 모델은 고전 역학의 법칙과 일치하는 물리적 구현에 의존합니다.^[10]고전적인 설명은 상대적으로 많은 수의 원자로 구성된 특정 시스템에 대해서만 정확합니다.자연에 대한 좀 더 일반적인 설명은 양자역학에 의해 제공됩니다.양자 계산은 인공지능 처리 및 통신을 알리기 위한 목적으로 고전 근사치 범위를 넘어서는 양자 현상 응용을 연구합니다.양자 계산의 다양한 모델이 존재하지만 가장 인기 있는 모델은 큐비트와 양자 게이트(또는 게이트 기반 초전도 양자 컴퓨팅)의 개념을 통합합니다.

초전도체는 낮은 온도에서 거의 무한대의 전도성과 거의 제로의 저항을 가지고 있기 때문에 구현됩니다.각 큐비트는 LC 회로가 있는 반도체 회로(커패시터 및 인덕터)를 사용하여 제작됩니다.^{[citation needed]}

열이 양자 정보를 방해할 수 있기 때문에 에너지를 거의 방출하지 않는 공진 회로를 만드는 데 초전도 커패시터와 인덕터가 사용됩니다.초전도 공명 회로는 큐비트로 사용될 수 있는 인공 원자의 한 종류입니다.양자 회로의 이론적 구현과 물리적 구현은 크게 다릅니다.양자 회로를 구현하는 것은 고유한 도전 과제를 가지고 있으며, 이론 물리학자 데이비드 P 디빈센조가 제안한 조건, 초전도 양자 컴퓨팅의 물리적 구현을 위한 기준을 준수해야 합니다.^[11]여기서 초기 5개의 기준은 양자 컴퓨터가 양자역학의 가설과 일치하고 나머지 2개는 네트워크를 통해 이 정보를 전달하는 것과 관련된 것임을 보장합니다.^{[citation needed]}

우리는 이러한 원자들의 지면과 여기 상태를 0과 1 상태로 매핑합니다. 이는 이산적이고 구별되는 에너지 값이므로 양자역학의 가설과 일치하기 때문입니다.그러나 이러한 구조에서 전자는 여러 개의 다른 에너지 상태로 점프할 수 있고 우리의 들뜬 상태에 국한되지 않을 수 있습니다. 따라서 시스템은 바닥 상태에서 들뜬 상태로 점프하는 데 필요한 에너지 차이가 있는 광자에만 영향을 받도록 제한되어야 합니다.^[12]그러나 이것은 한 가지 중요한 문제를 남깁니다. 우리는 동일한 에너지를 가진 광자가 인접한 상태 쌍 사이에 전이를 일으키는 것을 방지하기 위해 에너지 수준 사이의 불균일한 간격이 필요합니다.조셉슨 접합은 큐비트 구현에 매우 중요한 비선형 인덕턴스를 가진 초전도 소자입니다.^[12]공진 초전도 회로에서 이 비선형 요소를 사용하면 에너지 레벨 사이에 불균일한 간격이 발생합니다.^{[citation needed]}

큐빗

큐비트는 두 상태의 양자 중첩을 차지할 수 있는 비트(두 가지 가능한 상태를 가진 시스템)의 일반화입니다.한편, 양자 게이트(quantum gate)는 논리 게이트의 초기 상태에서 게이트가 인가되면 하나 이상의 큐비트의 변환을 설명하는 일반화입니다.큐비트와 게이트의 물리적 구현은 양자 현상이 발생하는 미세한 규모를 고려할 때 일상 생활에서 관찰하기 어려운 것과 같은 이유로 어렵습니다.양자 컴퓨터를 달성하기 위한 한 가지 방법은 극도로 낮은 작동 온도의 가격이지만 양자 효과를 거시적으로 관찰할 수 있는 초전도체를 구현하는 것입니다.

초전도체

일반적인 전도체와 달리, 초전도체는 저항률이 거의 0으로 떨어지고 전도도가 급격히 증가하는 임계 온도를 가지고 있습니다.초전도체에서 기본 전하 전달자는 일반적인 전도체에서 볼 수 있는 단일 페르미온이 아니라 전자 쌍(구리 쌍으로 알려져 있음)입니다.^[13]쿠퍼 쌍은 느슨하게 결합되어 있고 페르미 에너지보다 낮은 에너지 상태를 가지고 있습니다.쿠퍼 쌍을 형성하는 전자는 동등한 반대 운동량과 스핀을 가지고 있으므로 쿠퍼 쌍의 전체 스핀은 정수 스핀입니다.따라서 쿠퍼 쌍은 보손입니다.초전도 큐비트 모델에 사용된 두 개의 초전도체는 니오븀과 탄탈륨이며 둘 다 d-밴드 초전도체입니다.^[14]

보스-아인슈타인 응축수

보손의 집합은 거의 절대 0까지 냉각되면 가장 낮은 에너지 양자 상태(바닥 상태)로 붕괴되어 보스-아인슈타인 응축수로 알려진 물질의 상태를 형성합니다.페르미온과 달리 보손은 동일한 양자 에너지 수준(또는 양자 상태)을 차지할 수 있으며 파울리 배제 원칙을 따르지 않습니다.고전적으로 보스-아인슈타인 응축수는 공간에서 동일한 위치를 차지하고 동일한 운동량을 갖는 다수의 입자로 개념화될 수 있습니다.보손 사이의 상호작용력이 최소화되기 때문에 보즈-아인슈타인 응축수가 효과적으로 초전도체 역할을 합니다.따라서 초전도체는 무한에 가까운 전도도와 거의 제로 저항을 모두 가지고 있기 때문에 양자 컴퓨팅에 구현됩니다.그렇다면 일반적인 전도체에 비해 초전도체의 장점은 이론적으로 거의 순간적으로 신호를 전송하고 에너지 손실 없이 무한히 달릴 수 있다는 점에서 두 가지입니다.NASA가 최근 우주 공간에서 보즈-아인슈타인 응축수가 중력의 제약 없이 더 쉽게 달성되고 (급속 소멸 없이) 더 오랜 시간 동안 유지되는 콜드 아톰 연구소를 개발한 것을 고려하면 초전도 양자 컴퓨터의 실현 가능성은 더욱 유망해집니다.^[15]

전기회로

초전도 전자 회로(전기 소자 네트워크)의 각 지점에서 전하 흐름을 설명하는 응축수 파동 함수는 어떤 복잡한 확률 진폭에 의해 잘 정의됩니다.일반적인 도체 전기 회로에서는 거시적 분석에서 다양한 파동 함수가 평균화되어 양자 효과를 관찰할 수 없다는 점을 제외하면 개별 전하 캐리어의 경우에도 동일한 설명이 적용됩니다.응축수 파동함수는 거시적 양자효과의 설계와 측정을 가능하게 하는데 유용하게 사용됩니다.보어 모델의 이산 원자 에너지 수준과 유사하게, 오직 이산 개수의 자속 양자만이 초전도 루프를 통과할 수 있습니다.두 경우 모두 양자화는 복잡한 진폭 연속성에서 비롯됩니다.양자 컴퓨터(원자나 광자 등)의 미시적 구현과는 달리, 초전도 회로의 매개 변수는 정전용량이나 인덕턴스를 조정하는 등 전기 요소에 (고전적인) 값을 설정하여 설계됩니다.

전기 회로에 대한 양자 역학적 설명을 얻으려면 몇 가지 단계가 필요합니다.첫째, 모든 전기 요소는 고전 회로에 사용되는 밀접하게 관련된 거시적 전류 및 전압 설명보다는 응축수 파동 함수 진폭 및 위상으로 설명해야 합니다.예를 들어, 공간의 임의의 지점에서 파동함수 진폭의 제곱은 전하 캐리어를 찾을 확률에 해당합니다.따라서 진폭 제곱은 고전적인 전하 분포에 해당합니다.전기 회로의 양자 역학적 설명을 얻기 위한 두 번째 요구 사항은 일반화된 키르히호프의 회로 법칙이 회로 네트워크의 모든 노드에 적용되어 시스템의 운동 방정식을 얻는 것입니다.마지막으로, 이러한 운동 방정식은 계의 총 에너지를 설명하는 양자 해밀턴이 유도되도록 라그랑지안 역학으로 재구성되어야 합니다.

테크놀러지

제조업

초전도 양자 컴퓨팅 장치는 일반적으로 무선 주파수 스펙트럼에서 설계되고, 15 mK(밀리켈빈) 미만의 희석 냉장고에서 냉각되며, 주파수 합성기 및 스펙트럼 분석기와 같은 기존 전자 기기로 처리됩니다.일반적인 치수는 마이크로미터 범위에 속하며, 서브마이크로미터 해상도를 통해 잘 확립된 집적 회로 기술로 해밀턴 시스템을 편리하게 설계할 수 있습니다.초전도 큐비트를 제조하는 것은 리소그래피, 금속 증착, 에칭 및 제어된 산화를 포함하는 프로세스를 따릅니다.^[16]제조업체들은 초전도 큐비트의 수명을 지속적으로 개선하고 있으며 2000년대 초반부터 상당한 개선을 이루어냈습니다.^[16]^{: 4}

조지프슨 교차점

초전도 양자 회로의 한 가지 구별할 수 있는 특성은 조셉슨 접합의 사용입니다.조셉슨 접합은 정상적인 도체에는 존재하지 않는 전기 소자입니다.접합은 절연체 재료의 두께가 몇 원자에 불과한 얇은 층 양쪽에 있는 두 개의 와이어 리드(이 경우 초전도 와이어) 사이의 약한 연결이며, 일반적으로 그림자 증발 기술을 사용하여 구현됩니다.그 결과 생성된 조셉슨 접합 장치는 접합부가 초전류를 생성하는 조셉슨 효과를 나타냅니다.단일 조셉슨 접합의 영상이 오른쪽에 표시됩니다.접합부의 두 면에 있는 응축수 파동함수는 약한 상관관계가 있으며, 이는 그들이 다른 초전도 위상을 갖도록 허용된다는 것을 의미합니다.이러한 비선형성의 차이는 접합부를 가로지르는 파동함수가 연속적이어야 하는 연속 초전도 와이어와 대비됩니다.접합부를 통한 전류 흐름은 양자 터널링에 의해 발생하며, 접합부의 한쪽에서 다른 쪽으로 순간적으로 "터널"되는 것으로 보입니다.이 터널링 현상은 양자계만의 현상입니다.따라서 양자 터널링은 $\Delta E$ 인덕턴스를 만드는 데 사용되며, 이는 에너지 레벨이 에너지 레벨 사이의 불균일한 간격으로 이산화(또는 양자화)되는 무조화 발진기의 설계를 가능하게 하며, 이는 δE {\ $displaystyle \Delta E}$ 로 표시됩니다 $\Delta E$ 대조적으로,양자 고조파 발진기는 큐비트로 사용할 수 없습니다. 두 가지 상태만 해결할 수 있는 방법이 없기 때문입니다.

큐빗 원형

세 가지 주요 초전도 큐빗 원형은 위상, 전하 및 플럭스 큐빗입니다.플럭소늄,^[17] 트란스몬,^[18] 엑스몬,^[19] 퀀트로늄을 포함한 이러한 원형들의 많은 혼성화들이 존재합니다.^[20]큐비트 구현의 경우 논리적 양자 상태 $\{|0\rangle ,|1\rangle \}$ { $\{|0\rangle ,|1\rangle \}$ ⟩ $\{|0\rangle ,|1\rangle \}$ $\{|0\rangle ,|1\rangle \}$ ⟩ } $\{0\rangle, 1\rangle \}$ 이(가) 물리적 시스템의 다양한 상태(일반적으로 이산 에너지 수준 또는 양자 중첩)에 매핑됩니다.세 원형은 각각 조셉슨 에너지 대 충전 에너지 비율의 상이한 범위를 가지고 있습니다.Josephson energy는 전류가 통과할 때 Josephson 접합부에 저장된 에너지를 의미하며, 충전 에너지는 Cooper 쌍 1개가 접합부의 전체 커패시턴스를 충전하는 데 필요한 에너지입니다.^[21]조셉슨 에너지는 쓸 수 있습니다.

$U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}cos\delta$ $=$ - $U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}cos\delta$ $U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}cos\delta$ $U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}cos\delta$ $U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}cos\delta$ $U_{j}=-{\frac {I_{0}\Phi _{0}}{2\pi }}cos\delta$ δ ${\displaystyle$ }=- {\ $frac {I_{0}\Phi$ _ ${0}}{2\pi$ elta $},$

여기서 I $I_{0}$ $I_{0}$ 은 조셉슨 접합의 임계 전류 매개 변수이고, φ $\Phi _{0}={\frac {h}{2e}}$ = $\Phi _{0}={\frac {h}{2e}}$ $\Phi _{0}={\frac {h}{2e}}$ $\Phi _{0}={\frac {h}{2e}}$ ${\displaystyle \Phi _{0$ }={\ $frac {h}{2e}}}$ 은(초전도) 플럭스 양자이고, δ ${\displaystyle$ \delta }은 접합에 걸친 위상 차이입니다. $cos\delta$ δ $cos\delta$ 이라는 항은 조셉슨 접합의 비선형성을 나타냅니다.전하 에너지가 기록됩니다.

$E_{C}={\frac {e^{2}}{2C}}$ $=$ $E_{C}={\frac {e^{2}}{2C}}$ $E_{C}={\frac {e^{2}}{2C}}$ ${\displaystyle$ }={\ $frac {e^{2}}{2C$

여기서 $C$ $C$ 는 $C$ 접합의 정전용량이고 $e$ $e$ 은 $e$ 전자 전하입니다.^[21]세 가지 원형 중 위상 큐비트는 대부분의 쿠퍼 쌍이 접합부를 통해 터널링하고 플럭스 큐비트가 그 뒤를 따르고 전하 큐비트가 가장 적게 허용합니다.

위상 큐비트

위상 큐비트는 크기 $10^{6}$ ${\$ 정도의 에너지를 충전하는 조셉슨을 가지고 있습니다 $10^{6}$ 위상 큐비트의 경우, 에너지 준위는 조셉슨 접합에 걸쳐 서로 다른 양자 전하 진동 진폭에 해당합니다.여기서 전하와 위상은 각각 운동량과 위치가 양자 조화 진동자와 유사합니다.이런 맥락에서 큐비트의 서로 다른 상태 사이의 위상이 아니라 초전도 파동 함수(초전도 순서 매개 변수라고도 함)의 복잡한 주장이 있다는 것에 주목하십시오.

플럭스 큐빗

플럭스 큐비트(영속 전류 큐비트라고도 함)는 크기 $10$ $10$ 정도로 충전 에너지에 대한 조셉슨 비율을 가지고 있습니다 $10$ 플럭스 큐비트의 경우, 에너지 레벨은 초전도 고리에 갇힌 다양한 정수의 자속 양자에 해당합니다.

플루소늄

플럭소늄 큐비트는 조셉슨 접합이 E $E_{J}\gg E_{L}$ ≫ $E_{J}\gg E_{L}$ $E_{J}\ggE_{L$ 의 선형 인덕터에 의해 션트되는 플럭소늄 큐비트의 특정 유형입니다. 여기서 $E_{L}=(\hbar /2e)^{2}/L$ = $E_{L}=(\hbar /2e)^{2}/L$ (ℏ $E_{L}=(\hbar /2e)^{2}/L$ / $E_{L}=(\hbar /2e)^{2}/L$ $E_{L}=(\hbar /2e)^{2}/L$ / $E_{L}=(\hbar /2e)^{2}/L$ ${\displaystyle E_{L$ }= (\ $hbar$ / $2e)^{2}/L$ 실제로,선형 인덕터는 보통 직렬로 연결된 큰 크기의 조셉슨 접합의 많은 수(종종 $N>100$ > $N>100$ ${\displaystyle N$ > 100 $}일$ 수 있음)로 구성된 조셉슨 접합 어레이에 의해 구현됩니다 $N>100$ 이 조건에서 플루소늄의 해밀토니안은 다음과 같이 쓸 수 있습니다.

$H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ $=$ 4 $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ + $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ 2 $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ - $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ J $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ - $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ ϕ $H=4E_{C}n^{2}+{\frac {1}{2}}E_{L}\phi ^{2}-E_{J}\cos(\phi -\phi _{ext})$ ${\displaysty$ H $=4E_{C}n^{2}+{\frac {1}{2}}\phi^{2}-E_{J}\cos(\phi$ - $\phi_{ext})}.$

플럭소늄 큐비트의 한 가지 중요한 장점은 1밀리초를 초과하는 반플럭스 스위트 스팟에서의 큐비트 수명이 더 길다는 것입니다.^[25]^[24]플럭소늄 큐비트를 기반으로 하는 2 큐비트 게이트는 긴 수명의 이점을 이용합니다.

충전큐빗

쿠퍼 쌍 상자라고도 불리는 전하 큐비트는 크기 $<1$ < $<1$ $<1$ 정도의 조셉슨 대 충전 에너지 비율을 가지고 있습니다 $<1$ 전하 큐비트의 경우 다른 에너지 수준은 초전도 섬(제어 가능한 전하 캐리어 수가 있는 작은 초전도 영역)의 정수 개의 쿠퍼 쌍에 해당합니다.^[26]실제로 실험적으로 실현된 최초의 큐비트는 1999년에 달성된 쿠퍼 쌍 상자입니다.^[27]

트란스몬

트랜스몬은 소음을 완화하도록 특별히 설계된 션트 커패시터를 가진 특별한 큐비트 유형입니다.트랜스몬 큐비트 모델은 Cooper 쌍 상자^[29](위의 1열 표에 표시됨)를 기반으로 합니다.이것은 또한 양자 우월성을 보여준 최초의 큐빗이었습니다.^[30]조지프슨 대 충전 에너지 비율이 증가하면 소음이 완화됩니다.커플링 캐패시터를 사용하여 두 개의 트랜스몬을 연결할 수 있습니다.^[1]이 2 큐비트 시스템의 경우 해밀토니안이 작성됩니다.

${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ $=$ ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ J ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ σ ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ x ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ 2 ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ + ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ $σ$ 2 ${\hat {H}}={\frac {\hbar J}{2}}(\sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y})$ ) ${\displaystyle {\h$ }}={\ $frac {\hbar$ J $}{2}}(\sigma$ _ ${$ sigma $_{2}^{y$

여기서 $J$ $J$ 는 전류 밀도이고 σ $\sigma$ 는 표면 전하 밀도입니다.

엑스몬

Xmon은 평면 트랜스몬 모델을 기반으로 유래했다는 점에서 트랜섬과 디자인이 매우 유사합니다.^[31]엑스몬은 본질적으로 조정 가능한 트랜스몬입니다.트랜스몬 큐비트와 엑스몬 큐비트의 가장 큰 차이점은 엑스몬 큐비트가 커패시터 패드 중 하나로 접지된다는 것입니다.^[32]

게이트몬

트랜스몬 큐비트의 또 다른 변형은 게이트몬입니다.엑스몬과 마찬가지로 게이트몬도 트랜스몬의 가변형입니다.게이트몬은 게이트 전압을 통해 조정할 수 있습니다.

유니몬

2022년, 핀란드의 IQM 퀀텀 컴퓨터, 알토 대학, VTT 기술 연구 센터의 연구원들은 유니몬이라고 알려진 새로운 초전도 큐비트를 발견했습니다.^[34]비교적 간단한 큐비트인 유니몬은 (초전도) 공진기 내부에 선형 인덕터(전류에 의존하지 않는 인덕턴스를 갖는)에 의해 션트된 단일 조셉슨 접합으로 구성됩니다.^[35]유니몬은 화성성을 높이고 작동 시간을 단축시켜 노이즈 오류에 대한 민감성을 낮췄습니다.^[35]유니몬 큐비트의 또 다른 장점으로는 불연성 증가 외에도 플럭스 노이즈에 대한 민감성 감소 및 dc 충전 노이즈에 대한 완전한 무감각이 있습니다.^[22]

초전도 큐빗 원형

유형 측면	충전큐빗	RF-SQUID 큐비트(Flux 큐비트의 프로토타입)	위상 큐비트
서킷	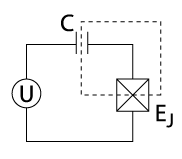충전 큐비트 회로.정전용량 $C$ $C$ 인 커패시터의 리드와 $U$ U $U$ 에 의해 바이어스된 $E_{J}$ 에너지 $E_{J}$ ${\$ 인 조셉슨 접합 사이에 초전도 섬(점선으로 둘러싸인)이 정의됩니다 $U$	플럭스 큐빗 회로.인덕턴스 $L$ 이 $L$ 인 초전도 루프는 조셉슨 에너지 $E_{J}$ $E_{J$ 와의 접합에 의해 중단됩니다 $E_{J}$ 바이어스 플럭스 φ $\Phi$ 는 전류 $I_{0}$ $I_{0$ 인 플럭스 라인에 의해 유도됩니다 $I_{0}$	위상 큐비트 회로.에너지 매개 변수 $E_{J}$ 가 $E_{J}$ {\ $displaystyle E_{J}$ 인 조셉슨 접합은 전류 $I_{0}$ ${\$ 에 의해 편향됩니다 $E_{J}$ $I_{0}$
해밀토니안	$H=E_{C}(N-N_{g})^{2}-E_{J}\cos \phi$ 이 경우 $N$ $N$ 은 접합을 통해 터널링할 Cooper 쌍의 수입니다. $N_{g}=CV_{0}/2e$ = $N_{g}=CV_{0}/2e$ 0 / ${\displaystyle N_{g$ }= $CV_{0}/2e}$ 는 쿠퍼 쌍 번호 단위로 커패시터의 전하입니다. $E_{C}=(2e)^{2}/2(C_{J}+C)$ $=$ $E_{C}=(2e)^{2}/2(C_{J}+C)$ $E_{C}=(2e)^{2}/2(C_{J}+C)$ / 2 $E_{C}=(2e)^{2}/2(C_{J}+C)$ $E_{C}=(2e)^{2}/2(C_{J}+C)$ + C $E_{C}=(2e)^{2}/2(C_{J}+C)$ ) ${\displaystyle E_{C$ } $=$ ( $2e)^{2}/2(C_{J}$ + $C)}$ 는 용량 C $C$ 및 조셉슨 접합 용량 C $C_{J}$ $C_{J}$ 와 모두에 연결된 충전 에너지입니다 $C_{J}$	$H={\frac {q^{2}}{2C_{J}}+\left({\frac {\Phi_0}}{2\pi}}\right)^2}{\frac {\phi^{2}}-E_{J}\cos \left[\phi -\pi {2\pi}{\frac {2\pi }{\Phi _{0}}\right]$ ϕ ${\displaystyle$ \phi}은 $($ 는) π ${\displaystyle$ 2\ $pi}$ 보다 $2\pi$ 큰 값만 취할 수 있으며 인덕턴스 L ${\displaystyle$ L}을 $($ 를 $L$ 따라 전압의 시간 적분으로 정의할 수도 있습니다.	$H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $=$ ( $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ ) $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ C $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ - $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $\Phi _{0}$ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ π ϕ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ - E $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ ⁡ ϕ ${\displaystyl$ H = {\ $frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _0}{2\pi }\phi -E_{J}\cos \phi }$ $H={\frac {(2e)^{2}}{2C_{J}}}q^{2}-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ 기서 φ 0 $\Phi _{0$ 은 자속 양자입니다.
잠재적인	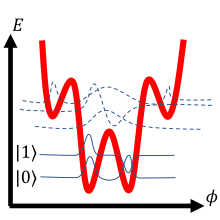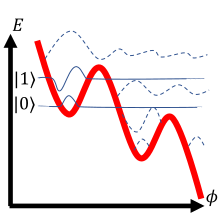$U=-E_{J}\cos \phi$ $=$ - E $U=-E_{J}\cos \phi$ $U=-E_{J}\cos \phi$ $\|0\rangle$ $U=-E_{J}\cos \phi$ ${\displaystyl$ U = - $E_{J}\cos \phi$ }. $U=-E_{J}\cos \phi$ $N_{g}={\frac {1}{2}}$ $N_{g}={\frac {1}{2}}$ $N_{g}={\frac {1}{2}}$ {\ $displaystyle N_$ $U=-E_{J}\cos \phi$ $g$ } = {\ $frac$ { $1}{2}}$ 가 되도록 바이어스 전압을 설정하여 $N_{g}={\frac {1}{2}}$ $\|0\rangle$ $\|1\rangle$ {\ $displaystyle$ 0\ $rangle}$ 과 $\|1\rangle$ ⟩ $1\rangle$ 사이의 에너지 갭을 최소화하여 다른 에너지 갭 $\|1\rangle$ 예: $\|1\rangle$ ⟩ ${\displaystyle 1\rangle})$ 과 $\|2\rangle$ ⟩ ${\displaystyle 2\rangle})$ 사이의 간격.공백 차이로 인해 $\|0\rangle$ ⟩ $0\rangle$ 에서 $\|1\rangle$ ⟩ ${\displaystyle 1\rangle}($ 으)로 주소를 변경할 수 있으며, 그 반대의 경우 다른 상태를 채우지 않습니다.	$U=\left({\frac {\Phi _{0}}{2\pi }}\right)^{2}{\frac {\phi ^{2}}{2L}}-E_{J}\cos \left[\phi -\Phi {\frac {2\pi }{\Phi _{0}}}\right]$ $Phi _{0}}\right]}}$ 바이어스 플럭스는 $φ$ $=$ $φ$ $\Phi =\Phi _{0}/2$ / $\Phi =\Phi _{0}/2$ ${\displaystyle \Phi$ $=$ \ $Phi _{0}/2}$ 입니다 $\Phi =\Phi _{0}/2$ 다른 웰은 초전도 루프에 갇힌 플럭스 양자의 구별된 수에 해당합니다.두 개의 낮은 상태는 0 또는 단일 갇힘 플럭스 양자의 대칭적이고 반대칭적인 중첩에 해당합니다. $\|0\rangle =\left[\|\circlearrowleft \rangle +\|\circlearrowright \rangle \right]/{\sqrt {2}}$ 방향 및 반시계 방향 루프 전류 상태로 표시되는 경우가 있습니다: $\|0\rangle =\left[\|\circlearrowleft \rangle +\|\circlearrowright \rangle \right]/{\sqrt {2}}$ ⟩ = [ $\|0\rangle =\left[\|\circlearrowleft \rangle +\|\circlearrowright \rangle \right]/{\sqrt {2}}$ ↺ ⟩ + ↻ ⟩ $\|0\rangle =\left[\|\circlearrowleft \rangle +\|\circlearrowright \rangle \right]/{\sqrt {2}}$ ] / $\|1\rangle =\left[\|\circlearrowleft \rangle -\|\circlearrowright \rangle \right]/{\sqrt {2}}$ $\|0\rangle =\left[\|\circlearrowleft \rangle +\|\circlearrowright \rangle \right]/{\sqrt {2}}$ {\ $displaystyle$ 0 $\rangle$ =\ $left[$ \ $circlerow$ left $\rangle$ + \ $circlerow$ right $\right$ ] / {\ $sqrt {2}}$ $\|1\rangle =\left[\|\circlearrowleft \rangle -\|\circlearrowright \rangle \right]/{\sqrt {2}}$ 1 ⟩ = [↺ ⟩ $\|1\rangle =\left[\|\circlearrowleft \rangle -\|\circlearrowright \rangle \right]/{\sqrt {2}}$ - $\|1\rangle =\left[\|\circlearrowleft \rangle -\|\circlearrowright \rangle \right]/{\sqrt {2}}$ ↻ ⟩ $\|1\rangle =\left[\|\circlearrowleft \rangle -\|\circlearrowright \rangle \right]/{\sqrt {2}}$ / 2 $\|1\rangle =\left[\|\circlearrowleft \rangle -\|\circlearrowright \rangle \right]/{\sqrt {2}}$ {\ $displaystyle 1\rangle$ =\ $left[$ \ $circlearrow$ left \ $rangle$ - \ $circlearrow$ right $\right]$ / ${\sqrt {2}}.$	$U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $=$ - $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ π ϕ $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ - E $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ ⁡ ϕ ${\displaysty$ U=- $I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi },$ 일명 "워시보드" 전위입니다 $U=-I_{0}{\frac {\Phi _{0}}{2\pi }}\phi -E_{J}\cos \phi$ 바이어스 전류는 정확히 두 개의 국부적인 파동 함수를 포함할 수 있을 정도로 얕은 웰을 허용하도록 조정됩니다.바이어스 전류가 약간 증가하면 측정 가능한 전압 스파이크( $\|1\rangle$ 큐비트 측정에 일반적으로 사용되는 메커니즘)로 표현되는 높은 에너지 상태(1 ⟩ ${\displaystyle 1\rangle})$ 의 선택적 "스필"이 발생합니다.

위의 표에서 세 가지 초전도 큐빗 원형을 검토합니다.첫 번째 행에는 큐비트의 전기 회로도가 제시되어 있습니다.두 번째 행은 회로에서 파생된 양자 해밀토니안을 묘사합니다.일반적으로 해밀토니안은 계의 운동 및 퍼텐셜 에너지 성분의 합입니다(퍼텐셜 우물의 입자와 유사).해밀토니안의 $\phi$ , $\phi$ ϕ {\ $displaystyle$ \ $phi}$ 는 접합에 걸친 초전도 파동 함수 위상 차이, C $C_{J}$ $C_{J$ 는 조셉슨 접합과 관련된 정전용량, $q$ $q$ 는 접합 정전용량의 전하입니다.표시된 각 전위에 대해 계산에는 고체 파동 함수만 사용됩니다.큐비트 전위는 굵은 빨간색 선으로 표시되며, 개략적인 파동 함수 솔루션은 명확한 설명을 위해 적절한 에너지 레벨로 들어올려진 얇은 선으로 표시됩니다.

입자 질량은 회로 용량의 역함수에 해당하며 퍼텐셜의 모양은 정규 인덕터와 조셉슨 접합에 의해 결정됩니다.표의 세 번째 행에 있는 개략적인 파동 솔루션은 위상 변수의 복잡한 진폭을 보여줍니다.구체적으로, 큐비트가 특정 상태를 차지하는 동안 큐비트의 위상이 측정되면, 묘사된 파동 함수가 진동하는 곳에서만 특정 값을 측정할 확률이 0이 아닙니다.세 행 모두 동일한 물리적 시스템의 기본적으로 서로 다른 표현입니다.

단 큐비트

초전도 큐비트의 에너지 레벨 사이의 GHz 에너지 갭은 테라헤르츠 갭(고주파 대역의 장비 부족)으로 인해 사용 가능한 전자 장비와 호환되도록 설계되었습니다.초전도체 에너지 갭은 쿠퍼 쌍이 깨지는 ~1THz 이하의 동작의 상한을 의미하므로 에너지 레벨 분리가 너무 높을 수 없습니다.반면, 냉각을 고려할 때 에너지 준위의 분리는 너무 작을 수 없습니다. 1K의 온도는 20GHz의 에너지 변동을 의미합니다.희석식 냉장고에서 수십 밀리켈빈의 온도를 얻을 수 있으며 ~5 GHz 에너지 레벨 분리에서 큐비트 작동이 가능합니다.큐비트 에너지 레벨 분리는 전용 바이어스 전류 라인을 제어하여 큐비트 파라미터를 미세 조정하는 "노브"를 제공함으로써 자주 조정됩니다.

단일 큐비트 게이트

단일 큐비트 게이트는 Bloch 구의 회전에 의해 달성됩니다.단일 큐비트의 서로 다른 에너지 레벨 사이의 회전은 레벨 사이의 에너지 분리와 함께 공진하는 주파수와 함께 큐비트에 연결된 안테나 또는 전송 라인으로 전송된 마이크로파 펄스에 의해 유도됩니다.개별 큐비트는 전용 전송 라인에 의해 또는 다른 큐비트가 공진을 해제한 경우 공유된 전송 라인에 의해 어드레싱될 수 있습니다.회전축은 마이크로파 펄스의 직교 진폭 변조에 의해 설정되며 펄스 길이는 회전 각도를 결정합니다.^[37]

구동 신호에 대해 보다 공식적으로(의 표기를 따름)

${\mathcal {E}}(t)={\mathcal {E}^{x}(t)\cos(\omega_{d}t)+{\mathcal {E}^{y}(t)\sin(\omega_{d}t)$

주파수 ω $\omega_{d}$ 의 $\omega _{d}$ 회전파 근사치에서 구동 큐비트 해밀턴은

$H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ $=$ ( $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ - $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ ) ⟩ ⟨ 1 + $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ ( $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ ) $σ$ x + $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ ( $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ ) $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ $H^{R}/\hbar =(\omega -\omega _{d})|1\rangle \langle 1|+{\frac {{\mathcal {E}}^{x}(t)}{2}}\sigma _{x}+{\frac {{\mathcal {E}}^{y}(t)}{2}}\sigma _{y}$ ${\displaystyle H^{R}/\$ =(\omega -\ $omega _{d}) 1\ran$ 1 + {\ $frac {{\mathcal {E}}^{x}(t){2}}\sigma$ _ ${x}+{\frac {\mathcal {E}^{2}},$ \ $sigma$ _ ${y$

여기서 ω $\omega$ 는 큐비트 공명이고 σ $\sigma _{x},\sigma _{y}$ σ $\sigma _{x},\sigma _{y}$ $\sigma_{x},\sigma_{y$ 는 파울리 행렬입니다.

$X$ $X$ 축을 중심으로 회전을 구현하려면 ${\mathcal {E}}^{y}(t)=0$ ${\mathcal {E}}^{y}(t)=0$ = 0 ${\displaystyle {\mathcal$ {E}}^{ $y}(t$ )= $0}$ ${\mathcal {E}}^{y}(t)=0$ $t_{g}$ $t_{g$ 동안 주파수 ω $\omega _{d}=\omega$ = ω ${\displaystyle \omega$ _ ${d$ }=\ $omega }$ 에서 마이크로파 펄스를 인가할 수 있습니다 $t_{g}$ 결과적인 변환은

${\displaystyle$ $H^{R}dt\right\}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t$

Bloch 구의 $X$ $X$ 축에 대한 회전 연산자 $R_{X}(\theta )$ ( θ $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ ) {\ $displaystyle R_{X}(\$ $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ $)},$ 각도 ∫ θ 0 $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ E ( $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ t $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ ) $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ $\theta =\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt$ ${\displaystyle \theta$ = $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt}$ 입니다. $Y$ $Y$ 축에 $Y$ 대한 회전도 비슷한 방식으로 구현할 수 있습니다.모든 단일 큐비트 유니터리 $U$ U $U$ 는 $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ = R $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ (θ $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ ) R $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ (θ $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ ) R $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ (θ $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ ) ${\displaystyle$ U= $R_{X}(\theta _{1})$ 로 표시될 수 있으므로 두 회전 연산자를 보여주는 것으로 보편성을 만족시키기에 충분합니다. $R_{Y}(\theta_{2})$ $X-Y$ - $X-Y$ $X-Y$ 분해라고 $X-Y$ 알려진 절차에 의해 $R_{X}(\theta _{3})($ 물리적으로 중요하지 않은 전역 위상까지). $U=R_{X}(\theta _{1})R_{Y}(\theta _{2})R_{X}(\theta _{3})$ ^[38]∫ $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ 0 t $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ ( $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ ) $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ = $\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt=\pi$ π ${\displaystyle$ \int _{ $0}^{$ t_{ $g}}{\mathcal$ { $E}}^{x$ }(t $)dt$ =\ $pi$ }을 $($ 를) 설정하면 변환이 발생합니다.

$U_{x}=\exp \left\{-i\int _{0}^{t_{g}}{\mathcal {E}}^{x}(t)dt\cdot \sigma _{x}/2\right\}=e^{-i\pi \sigma _{x}/2}=-i\sigma _{x}$

글로벌 위상 $-i$ $-i$ 까지 $-i$ NOT 게이트로 알려져 있습니다.

큐비트 연결

큐비트를 연결하는 기능은 2-큐비트 게이트를 구현하는 데 필수적입니다.중간 전기 커플링 회로에 두 큐비트를 연결하면 두 큐비트를 커플링할 수 있습니다.회로는 고정 요소(예: 커패시터)이거나 제어 가능(DC-SQUID)일 수 있습니다.첫 번째 경우, 게이트가 꺼지는 동안 큐비트를 분리하는 것은 큐비트를 공진에서 다른 것으로 튜닝하여 계산 상태 간의 에너지 갭을 다르게 함으로써 달성됩니다.^[39]이 접근 방식은 물리적 전기 회로가 연결된 큐비트 사이에 배치되어야 하기 때문에 본질적으로 가장 가까운 이웃 커플링으로 제한됩니다.특히, D-Wave Systems의 가장 가까운 이웃 커플링은 키메라 그래프 구성에서 8큐비트의 고도로 연결된 단위 셀을 달성합니다.양자 알고리즘은 일반적으로 임의 큐비트 간의 결합을 필요로 합니다.따라서 프로세서 비간섭 전에 가능한 양자 계산 기간을 제한하는 다중 스왑 작업이 필요합니다.

퀀텀 버스

두 개 이상의 큐비트를 연결하는 또 다른 방법은 양자 버스를 통해 큐비트를 중간체에 연결하는 것입니다.양자 버스는 종종 양자 고조파 발진기에 의해 모델링된 마이크로파 공동으로 구현됩니다.커플링 큐비트는 버스와 공진을 주고 받을 수 있으며 서로 연결되어 가장 가까운 이웃의 제한을 제거할 수 있습니다.결합을 설명하는 형식주의는 공동 양자 전기역학입니다.공동 양자 전기역학에서 큐비트는 원자가 전자기 복사의 THz 체제가 아닌 GHz의 차이를 가진 광 광자 공동과 상호 작용하는 것과 유사합니다.이러한 인공 원자 사이의 공진 여기 교환은 멀티 큐비트 게이트의 직접 구현에 잠재적으로 유용합니다.^[40]어두운 상태 다양체에 이어 Khazali-Mølmer 기법은^[40] 복잡한 멀티 큐비트 연산을 단일 단계로 수행하여 기존 회로 모델에 대한 실질적인 단축을 제공합니다.

크로스 공진 게이트

일반적인 게이팅 메커니즘 중 하나는 큐비트 2개와 버스 1개를 사용하며, 각각 다른 에너지 레벨 분리에 맞춰 조정됩니다.두 번째 큐비트와 공진하는 주파수를 가진 첫 번째 큐비트에 마이크로파 여기를 적용하면 두 번째 큐비트의 σ $\sigma _{x}$ $\sigma_{x}$ 회전이 발생합니다.회전 방향은 첫 번째 큐비트의 상태에 따라 달라지므로 제어된 위상 게이트 구성이 가능합니다.^[41]

의 표기법에 따라 첫번째 큐비트 구동선을 통해 여기계를 설명하는 해밀토니안 드라이브가 공식적으로 작성됩니다.^[41]

$=$ $I\otimes \sigma _{x}\right$

여기서 $A(t)$ $A(t)$ 는 마이크로파 펄스의 시간 모양이고, ω ~ 2 ${\tilde {\omega}}_{2$ 는 두 번째 큐비트의 공진 주파수, {I $\{I,\sigma _{x},\sigma _{y},\sigma _{z}\}$ σ $\{I,\sigma _{x},\sigma _{y},\sigma _{z}\}$ σ y, $\{I,\sigma _{x},\sigma _{y},\sigma _{z}\}$ σ $\{I,\sigma _{x},\sigma _{y},\sigma _{z}\}$ ${\displaystyle \{I,\sigma$ _ ${x},\sigma$ _ ${y},\sigma$ _ ${z}\}$ 는 파울리 행렬이고, $J$ $J$ 는 두 큐비트 사이의 결합 계수입니다.공진기, δ $\Delta _{12}\equiv \omega _{1}-\omega _{2}$ ≡ ω $\Delta _{12}\equiv \omega _{1}-\omega _{2}$ - $\Delta _{12}\equiv \omega _{1}-\omega _{2}$ ω 2 $\Delta _{12}\equiv \omega _{1}-\omega _{2}$ 는 큐비트 디튜닝, $m_{12}$ $m_{12}$ {\ $displaystyle m_{12}$ 은 큐비트 사이의 스트레이(원하지 않는) 커플링, ℏ $\hbar$ 는 플랑크 상수를 π $2\pi$ 로 나눈 값입니다 $2\pi$ $A(t)$ $A(t)$ 위의 시간 적분에 따라 회전 각도가 결정됩니다 $A(t)$ .해밀턴의 첫 번째 항과 세 번째 항에서 원하지 않는 회전은 단일 큐비트 연산으로 보상될 수 있습니다.나머지 구성 요소는 단일 큐비트 회전과 결합하여 su(4) Li 대수의 기초를 형성합니다.

큐비트 읽기

아키텍처별 판독 또는 측정 메커니즘이 존재합니다.위상 큐비트의 읽기는 위의 큐비트 원형 표에서 설명됩니다.플럭스 큐빗 상태는 종종 조정 가능한 DC-SQUID 자력계를 사용하여 읽습니다.전자계를 사용하여 상태를 측정할 수도 있습니다.^[1]보다 일반적인 리드아웃 방식은 마이크로웨이브 공진기에 대한 커플링을 포함하며, 여기서 공진기의 공진 주파수는 큐비트 상태에 의해 분산되어 이동됩니다.^[42]^[43]

디빈센조의 기준

디빈센조의 기준은 논리 큐비트를 구현할 수 있는 물리적 시스템의 요구 사항을 설명하는 목록입니다.디빈센조의 기준은 초전도 양자 컴퓨팅 구현으로 충족됩니다.초전도 양자 컴퓨팅에서의 현재 개발 노력의 대부분은 추가적인 리소그래피 층을 사용하여 3차원에서 상호 연결, 제어 및 판독을 달성하는 것을 목표로 합니다.논리 큐비트를 구현하기 위한 물리적 시스템에 대한 디빈센조의 기준의 목록은 초전도 큐비트의 구현에 의해 충족됩니다.당초 제안된 디빈센조의 기준은 양자컴퓨터를 물리적으로 구현하는 데 필요한 5가지 기준으로 구성돼 있지만, '양자 인터넷'으로 알려진 컴퓨터 간 양자 정보를 전송할 수 있는 컴퓨터 네트워크를 통한 통신을 고려한 것이어서 더 완전한 목록은 7가지 기준으로 구성돼 있습니다.따라서 처음 5개의 기준은 성공적인 양자 컴퓨팅을 보장하는 반면, 마지막 2개의 기준은 양자 통신을 허용합니다.

큐비트를 잘 특성화한 확장 가능한 물리적 시스템."잘 특성화된 것은 해밀턴 함수가 잘 정의되어야 한다는 것을 의미합니다. 즉 큐비트의 에너지 고유 상태가 정량화될 수 있어야 합니다.확장 가능한 시스템은 스스로 설명할 수 있으며, 큐비트를 조절하는 이 능력이 여러 큐비트에 대해 증가할 수 있어야 함을 나타냅니다.여기에 퀀텀 컴퓨터가 직면한 주요 문제가 있습니다. 더 많은 큐비트가 구현되면 비용 및 기타 물리적 구현이 기하급수적으로 증가하게 되며, 이는 향상된 속도에 비해 크게 부족합니다.^[11]초전도 큐비트는 칩에서 제작되기 때문에, 다중 큐비트 시스템은 쉽게 확장할 수 있습니다.큐비트는 칩의 2D 표면에 할당됩니다.잘 특성화된 큐비트에 대한 수요는 (a) 큐비트 비선형성(사용 가능한 에너지 레벨 중 두 개만 액세스) 및 (b) 큐비트당 전용 제어 라인 및/또는 주파수 분리 또는 튜닝을 통해 한 번에(전체 다수 큐비트 시스템이 아닌) 단일 큐비트에 액세스함으로써 충족됩니다.
큐비트 상태를 간단한 기준 상태로 초기화하는 기능.^[44]기준 상태는 쉽고 지속적으로 복제 가능하며 큐비트의 초기 상태를 보장하는 데 사용될 수 있기 때문에 양자 컴퓨팅에서 유용합니다.초전도 큐비트를 초기화하는 한 가지 간단한 방법은 큐비트가 바닥 상태로 이완될 때까지 충분히 오래 기다리는 것입니다.튜닝 노브로 큐비트 전위를 제어하면 더 빠른 초기화 메커니즘이 가능합니다.
관련된 긴 비간섭 시간^[44].초전도 큐비트의 비간섭성은 여러 요인에 의해 영향을 받습니다.대부분의 비간섭성은 조셉슨 접합의 품질과 칩 기판의 불완전성에 기인합니다.초전도 큐빗은 중경 스케일 때문에 상대적으로 수명이 짧습니다.그럼에도 불구하고, 이러한 다중 큐비트 시스템에서 수천 개의 게이트 동작이 입증되었습니다.^[45]
양자 게이트의 "보편적인" 집합입니다.^[44]초전도 큐비트는 단일 큐비트 게이트를 구현하면서 펄스 마이크로파 신호로 Bloch 구의 임의 회전을 허용합니다. $\sigma _{z}\sigma _{z}$ $\sigma _{x}\sigma _{x}$ $\sigma _{z}\sigma _{z}$ z ${\displayst$ $sigma$ _ ${z$ 및 $\sigma _{z}\sigma _{z}$ $\sigma _{x}\sigma _{x}$ $x$ $\sigma _{x}\sigma _{x}$ x ${\displayst$ $\sigma _{z}\sigma _{z}$ $sigma$ $\sigma _{z}\sigma _{z}$ $sigma$ _ ${x}}$ 커플링은 대부분의 구현과 범용 게이트 세트를 보완하기 위해 표시됩니다.이 기준은 두 개의 트랜스몬을 커플링 커패시터와 결합함으로써도 충족될 수 있습니다.^[1]
큐비트별 측정 능력.^[44]일반적으로 단일 초전도 큐비트는 제어 또는 측정을 위해 사용됩니다.
고정 큐비트와 플라잉 큐비트의 상호 변환성.^[44]고정 큐비트는 정보를 저장하거나 계산을 수행하는 데 사용되는 반면, 플라잉 큐비트는 거시적으로 정보를 전송합니다.큐비트는 정지 큐비트에서 플라잉 큐비트로 변환할 수 있어야 합니다.
지정된 위치 간에 플라잉 큐비트의 신뢰성 있는 전송.^[44]

마지막 두 가지 기준은 ETH가 동축 케이블로 연결된 두 개의 초전도 큐비트로 수행한 연구로 실험적으로 입증되었습니다.^[48]

과제들

초전도 양자 컴퓨팅의 주요 과제 중 하나는 보스-아인슈타인 응축물과 같은 초전도체가 존재하는 극도로 낮은 온도입니다.초전도 큐빗 설계의 다른 기본적인 과제는 잠재력을 잘 형성하고 두 특정 에너지 수준 사이의 에너지 분리가 독특하도록 입자 질량을 선택하는 것인데, 이는 이 두 수준이 큐빗의 논리적 상태로 사용되기 때문입니다.

또한 초전도 양자 컴퓨팅은 양자 잡음(환경과의 상호작용으로 인한 시스템 장애)과 누출(주변 환경에 대한 정보 손실)을 완화해야 합니다.누출을 줄이는 한 가지 방법은 패리티 측정입니다.^[16]초전도 양자 컴퓨팅이 직면한 많은 현재의 과제는 마이크로파 공학 분야에 있습니다.^[42]초전도 양자 컴퓨팅이 더 큰 규모의 장치에 접근함에 따라 연구자들은 큐비트 일관성, 확장 가능한 교정 소프트웨어, 전체 칩에 걸친 양자 상태의 효율적인 충실도 결정, 큐비트 및 게이트 충실도에서 어려움에 직면합니다.^[16]또한, 초전도 양자 컴퓨팅 장치는 이러한 개선 사항과 호환되도록 점점 더 큰 규모로 안정적으로 재현 가능해야 합니다.^[16]

초전도 양자 컴퓨팅의 여정:

최신 개발은 아니지만, 1990년대 후반 조셉슨 접합을 가로지르는 양자 터널링이 명백해졌을 때 초전도 큐비트로 초점이 옮겨지기 시작했고, 이는 이러한 초전도 큐비트를 통해 양자 컴퓨팅이 달성될 수 있다는 것을 실현할 수 있게 했습니다.^[49]

1999년, 나카무라 야스노부에 의해 논문이 발표되었는데, 이 논문은 초전도^[50] 큐비트의 초기 설계를 보여주었으며, 현재는 "전하 큐비트"로 알려져 있습니다.이는 이후 설계가 수정된 주요 기준점입니다.이러한 초기 큐비트는 긴 코히어런스 시간과 파괴적인 측정을 유지하는 데 있어서 한계가 있었습니다.이러한 초기 돌파구에 대한 추가적인 수정은 위상 및 플럭스 큐비트의 발명으로 이어졌으며, 그 결과 현재 광범위하고 주로 초전도 양자 컴퓨팅에 사용되는 트랜스몬 큐비트가 탄생했습니다.트랜스몬 큐비트는 독창적인 디자인을 강화했으며 큐비트에서 나오는 전하 소음을 더욱 완화시켰습니다.^[49]

이 여정은 길고, 고되고, 돌파구로 가득 차 있었지만, 최근 역사에서 상당한 발전을 이루었고, 컴퓨팅 혁신에 엄청난 잠재력을 가지고 있습니다.

초전도 양자 컴퓨팅의 미래:

Google, IBM 및 Baidu와 같은 업계 선두 기업들은 양자 컴퓨팅 분야에서 비약적인 발전을 이루기 위해 초전도 양자 컴퓨팅과 트랜스몬 큐비트를 사용하고 있습니다.

2022년 8월, 바이두는 초전도 큐비트를 통합한 완전 통합형 탑 투 바텀 양자 컴퓨터를 구축할 계획을 발표했습니다.이 컴퓨터는 하드웨어, 소프트웨어 및 응용프로그램을 모두 완벽하게 통합할 것입니다.이것은 양자 컴퓨팅 세계에서 최초이며 획기적인 발전을 이끌 것입니다.^[51]

IBM은 초전도 큐비트와 트랜스몬 큐비트를 통합한 양자 컴퓨터를 위해 설정한 로드맵을 공개했습니다.

2021년: IBM은 127 큐비트 프로세서를 출시했습니다.^[52]

2022년: 11월 9일, IBM은 433 큐비트 프로세서 "오스프리"를 발표했습니다.^[53]

2023: IBM은 1,121 큐비트의 Condor 퀀텀 프로세서를 출시할 계획입니다.^[52]

2024: IBM은 1,386 큐비트 이상의 플라밍고 퀀텀 프로세서를 출시할 계획입니다.^[52]

2025: IBM은 4,158개 이상의 큐비트를 갖춘 Kukaburra 퀀텀 프로세서를 출시할 계획입니다.^[52]

2026년 이후: IBM은 10,000 큐비트를 넘어 100,000 큐비트로 확장된 양자 프로세서를 출시할 계획입니다.^[52]

2016년 구글은 페르미-허바드 모델의 시연을 전달하기 위해 16 큐비트를 구현했습니다.또 다른 최근 실험에서 구글은 쉐링턴-커크패트릭 모델을 최적화하기 위해 17큐비트를 사용했습니다.구글은 고전적인 컴퓨터에서 1만년이 걸렸을 작업을 200초만에 수행하는 Sycamore 양자 컴퓨터를 생산했습니다.^[54]

참고문헌

^ ^a ^b ^c ^d ^e ^f "PennyLane Documentation — PennyLane". docs.pennylane.ai. Retrieved 2022-12-11.
^ Castelvecchi, Davide (5 January 2017). "Quantum computers ready to leap out of the lab in 2017". Nature. 541 (7635): 9–10. Bibcode:2017Natur.541....9C. doi:10.1038/541009a. PMID 28054624. S2CID 4447373.
^ ^a ^b "IBM Makes Quantum Computing Available on IBM Cloud". www-03.ibm.com. 4 May 2016.
^ "Imec enters the race to unleash quantum computing with silicon qubits". www.imec-int.com. Retrieved 2019-11-10.
^ 콜마 라이언, 블레이크 R.존슨, 디에고 리스테, 브라이언 도노반, 토마스 A.Ohki, "동적 양자 컴퓨팅을 위한 하드웨어", arXiv:1704.08314v1
^ "Rigetti Launches Quantum Cloud Services, Announces $1Million Challenge". HPCwire. 2018-09-07. Retrieved 2018-09-16.
^ "Intel Invests US$50 Million to Advance Quantum Computing Intel Newsroom". Intel Newsroom.
^ Kelly, J.; Barends, R.; Fowler, A. G.; Megrant, A.; Jeffrey, E.; White, T. C.; Sank, D.; Mutus, J. Y.; Campbell, B.; Chen, Yu; Chen, Z.; Chiaro, B.; Dunsworth, A.; Hoi, I.-C.; Neill, C.; O’Malley, P. J. J.; Quintana, C.; Roushan, P.; Vainsencher, A.; Wenner, J.; Cleland, A. N.; Martinis, John M. (4 March 2015). "State preservation by repetitive error detection in a superconducting quantum circuit". Nature. 519 (7541): 66–69. arXiv:1411.7403. Bibcode:2015Natur.519...66K. doi:10.1038/nature14270. PMID 25739628. S2CID 3032369.
^ Arute, Frank; Arya, Kunal; Babbush, Ryan; Bacon, Dave; Bardin, Joseph C.; Barends, Rami; Biswas, Rupak; Boixo, Sergio; Brandao, Fernando G. S. L.; Buell, David A.; Burkett, Brian; Chen, Yu; Chen, Zijun; Chiaro, Ben; Collins, Roberto; Courtney, William; Dunsworth, Andrew; Farhi, Edward; Foxen, Brooks; Fowler, Austin; Gidney, Craig; Giustina, Marissa; Graff, Rob; Guerin, Keith; Habegger, Steve; Harrigan, Matthew P.; Hartmann, Michael J.; Ho, Alan; Hoffmann, Markus; Huang, Trent; Humble, Travis S.; Isakov, Sergei V.; Jeffrey, Evan; Jiang, Zhang; Kafri, Dvir; Kechedzhi, Kostyantyn; Kelly, Julian; Klimov, Paul V.; Knysh, Sergey; Korotkov, Alexander; Kostritsa, Fedor; Landhuis, David; Lindmark, Mike; Lucero, Erik; Lyakh, Dmitry; Mandrà, Salvatore; McClean, Jarrod R.; McEwen, Matthew; Megrant, Anthony; Mi, Xiao; Michielsen, Kristel; Mohseni, Masoud; Mutus, Josh; Naaman, Ofer; Neeley, Matthew; Neill, Charles; Niu, Murphy Yuezhen; Ostby, Eric; Petukhov, Andre; Platt, John C.; Quintana, Chris; Rieffel, Eleanor G.; Roushan, Pedram; Rubin, Nicholas C.; Sank, Daniel; Satzinger, Kevin J.; Smelyanskiy, Vadim; Sung, Kevin J.; Trevithick, Matthew D.; Vainsencher, Amit; Villalonga, Benjamin; White, Theodore; Yao, Z. Jamie; Yeh, Ping; Zalcman, Adam; Neven, Hartmut; Martinis, John M. (October 2019). "Quantum supremacy using a programmable superconducting processor". Nature. 574 (7779): 505–510. arXiv:1910.11333. Bibcode:2019Natur.574..505A. doi:10.1038/s41586-019-1666-5. PMID 31645734.
^ Dayal, Geeta. "LEGO Turing Machine Is Simple, Yet Sublime". WIRED.
^ ^a ^b "DiVincenzo's Criteria - Quantum Computing Codex". qc-at-davis.github.io. Retrieved 2022-12-13.
^ ^a ^b Ballon, Alvaro (22 March 2022). "Quantum computing with superconducting qubits — PennyLane". Pennylane Demos. Retrieved 2022-12-13.
^ "Cooper Pairs".{{cite web}}: CS1 유지 : url-status (링크)
^ Shen, L. Y. L. (1972-02-01). "Superconductivity of Tantalum, Niobium and Lanthanum Studied by Electron Tunneling: Problems of Surface Contamination". AIP Conference Proceedings. 4 (1): 31–44. Bibcode:1972AIPC....4...31S. doi:10.1063/1.2946195. ISSN 0094-243X.
^ Greicius, Tony (2020-06-12). "NASA's Cold Atom Lab Takes One Giant Leap for Quantum Science". NASA. Retrieved 2022-12-11.
^ ^a ^b ^c ^d ^e Kjaergaard, Morten; Schwartz, Mollie E.; Braumüller, Jochen; Krantz, Philip; Wang, Joel I.-Jan; Gustavsson, Simon; Oliver, William D. (2020-03-10). "Superconducting Qubits: Current State of Play". Annual Review of Condensed Matter Physics. 11 (1): 369–395. arXiv:1905.13641. Bibcode:2020ARCMP..11..369K. doi:10.1146/annurev-conmatphys-031119-050605. ISSN 1947-5454. S2CID 173188891.
^ Manucharyan, V. E.; Koch, J.; Glazman, L. I.; Devoret, M. H. (1 October 2009). "Fluxonium: Single Cooper-Pair Circuit Free of Charge Offsets". Science. 326 (5949): 113–116. arXiv:0906.0831. Bibcode:2009Sci...326..113M. doi:10.1126/science.1175552. PMID 19797655. S2CID 17645288.
^ Houck, A. A.; Koch, Jens; Devoret, M. H.; Girvin, S. M.; Schoelkopf, R. J. (11 February 2009). "Life after charge noise: recent results with transmon qubits". Quantum Information Processing. 8 (2–3): 105–115. arXiv:0812.1865. doi:10.1007/s11128-009-0100-6. S2CID 27305073.
^ Barends, R.; Kelly, J.; Megrant, A.; Sank, D.; Jeffrey, E.; Chen, Y.; Yin, Y.; Chiaro, B.; Mutus, J.; Neill, C.; O’Malley, P.; Roushan, P.; Wenner, J.; White, T. C.; Cleland, A. N.; Martinis, John M. (22 August 2013). "Coherent Josephson Qubit Suitable for Scalable Quantum Integrated Circuits". Physical Review Letters. 111 (8): 080502. arXiv:1304.2322. Bibcode:2013PhRvL.111h0502B. doi:10.1103/PhysRevLett.111.080502. PMID 24010421. S2CID 27081288.
^ Metcalfe, M.; Boaknin, E.; Manucharyan, V.; Vijay, R.; Siddiqi, I.; Rigetti, C.; Frunzio, L.; Schoelkopf, R. J.; Devoret, M. H. (21 November 2007). "Measuring the decoherence of a quantronium qubit with the cavity bifurcation amplifier". Physical Review B. 76 (17): 174516. arXiv:0706.0765. Bibcode:2007PhRvB..76q4516M. doi:10.1103/PhysRevB.76.174516. S2CID 19088840.
^ ^a ^b ^c ^d Martinis, John M.; Osborne, Kevin (2004-02-16). "Superconducting Qubits and the Physics of Josephson Junctions". arXiv:cond-mat/0402415. Bibcode:2004cond.mat..2415M. {{cite journal}}:저널 요구사항 인용 journal=(도움말)
^ ^a ^b ^c Hyyppä, Eric; Kundu, Suman; Chan, Chun Fai; Gunyhó, András; Hotari, Juho; Janzso, David; Juliusson, Kristinn; Kiuru, Olavi; Kotilahti, Janne; Landra, Alessandro; Liu, Wei; Marxer, Fabian; Mäkinen, Akseli; Orgiazzi, Jean-Luc; Palma, Mario (2022-11-12). "Unimon qubit". Nature Communications. 13 (1): 6895. arXiv:2203.05896. Bibcode:2022NatCo..13.6895H. doi:10.1038/s41467-022-34614-w. ISSN 2041-1723. PMC 9653402. PMID 36371435.
^ ^a ^b Cottet, Nathanaël; Xiong, Haonan; Nguyen, Long B.; Lin, Yen-Hsiang; Manucharyan, Vladimir E. (2021-11-04). "Electron shelving of a superconducting artificial atom". Nature Communications. 12 (1): 6383. arXiv:2008.02423. Bibcode:2021NatCo..12.6383C. doi:10.1038/s41467-021-26686-x. ISSN 2041-1723. PMC 8569191. PMID 34737313.
^ ^a ^b Nguyen, Long B.; Lin, Yen-Hsiang; Somoroff, Aaron; Mencia, Raymond; Grabon, Nicholas; Manucharyan, Vladimir E. (2019-11-25). "High-Coherence Fluxonium Qubit". Physical Review X. 9 (4): 041041. arXiv:1810.11006. Bibcode:2019PhRvX...9d1041N. doi:10.1103/PhysRevX.9.041041. ISSN 2160-3308. S2CID 53499609.
^ Science, The National University of; MISIS, Technology. "Fluxonium qubits bring the creation of a quantum computer closer". phys.org. Retrieved 2022-12-12.
^ "Superconducting qubits – on islands, charge qubits and the transmon". LeftAsExercise. 2019-06-06. Retrieved 2022-12-12.
^ Wendin, G. (2017-10-01). "Quantum information processing with superconducting circuits: a review". Reports on Progress in Physics. 80 (10): 106001. arXiv:1610.02208. Bibcode:2017RPPh...80j6001W. doi:10.1088/1361-6633/aa7e1a. ISSN 0034-4885. PMID 28682303. S2CID 3940479.
^ Gambetta, J. M.; Chow, J. M.; Steffen, M. (2017). "Building logical qubits in a superconducting quantum computing system". npj Quantum Information. 3 (1): 2. arXiv:1510.04375. Bibcode:2017npjQI...3....2G. doi:10.1038/s41534-016-0004-0.
^ Roth, Thomas E.; Ma, Ruichao; Chew, Weng C. (2021-06-21). "An Introduction to the Transmon Qubit for Electromagnetic Engineers". arXiv:2106.11352. {{cite journal}}:저널 요구사항 인용 journal=(도움말)
^ Kjaergaard, Morten; Schwartz, Mollie E.; Braumüller, Jochen; Krantz, Philip; Wang, Joel I.-J.; Gustavsson, Simon; Oliver, William D. (2020-03-10). "Superconducting Qubits: Current State of Play". Annual Review of Condensed Matter Physics. 11 (1): 369–395. arXiv:1905.13641. Bibcode:2020ARCMP..11..369K. doi:10.1146/annurev-conmatphys-031119-050605. ISSN 1947-5454. S2CID 173188891.
^ Shim, Yun-Pil; Tahan, Charles (2016-03-17). "Semiconductor-inspired design principles for superconducting quantum computing". Nature Communications. 7 (1): 11059. arXiv:1507.07923. Bibcode:2016NatCo...711059S. doi:10.1038/ncomms11059. ISSN 2041-1723. PMC 4800439. PMID 26983379.
^ Wang, Chenlu; Li, Xuegang; Xu, Huikai; Li, Zhiyuan; Wang, Junhua; Yang, Zhen; Mi, Zhenyu; Liang, Xuehui; Su, Tang; Yang, Chuhong; Wang, Guangyue; Wang, Wenyan; Li, Yongchao; Chen, Mo; Li, Chengyao (2022-01-13). "Towards practical quantum computers: transmon qubit with a lifetime approaching 0.5 milliseconds". npj Quantum Information. 8 (1): 3. arXiv:2105.09890. Bibcode:2022npjQI...8....3W. doi:10.1038/s41534-021-00510-2. ISSN 2056-6387. S2CID 245950831.
^ "Fig. 1: Unimon qubit and its measurement setup. Nature Communications". {{cite journal}}:저널 요구사항 인용 journal=(도움말)
^ "Unimon: A new qubit to boost quantum computers from IQM IQM". www.meetiqm.com. Retrieved 2022-12-12.
^ ^a ^b Buchanan, Mark (2022-12-08). "Meet the Unimon, the New Qubit on the Block". Physics. 15: 191. Bibcode:2022PhyOJ..15..191B. doi:10.1103/Physics.15.191. S2CID 257514449.
^ Devoret, M. H.; Wallraff, A.; Martinis, J. M. (6 November 2004). "Superconducting Qubits: A Short Review". arXiv:cond-mat/0411174.
^ ^a ^b Motzoi, F.; Gambetta, J. M.; Rebentrost, P.; Wilhelm, F. K. (8 September 2009). "Simple Pulses for Elimination of Leakage in Weakly Nonlinear Qubits". Physical Review Letters. 103 (11): 110501. arXiv:0901.0534. Bibcode:2009PhRvL.103k0501M. doi:10.1103/PhysRevLett.103.110501. PMID 19792356. S2CID 7288207.
^ Chuang, Michael A. Nielsen & Isaac L. (2010). Quantum computation and quantum information (10th anniversary ed.). Cambridge: Cambridge University Press. pp. 174–176. ISBN 978-1-107-00217-3.
^ Rigetti, Chad Tyler (2009). Quantum gates for superconducting qubits. p. 21. Bibcode:2009PhDT........50R. ISBN 9781109198874.
^ ^a ^b Khazali, Mohammadsadegh; Mølmer, Klaus (2020-06-11). "Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits". Physical Review X. 10 (2): 021054. arXiv:2006.07035. Bibcode:2020PhRvX..10b1054K. doi:10.1103/PhysRevX.10.021054. ISSN 2160-3308.
^ ^a ^b Chow, Jerry M.; Córcoles, A. D.; Gambetta, Jay M.; Rigetti, Chad; Johnson, B. R.; Smolin, John A.; Rozen, J. R.; Keefe, George A.; Rothwell, Mary B.; Ketchen, Mark B.; Steffen, M. (17 August 2011). "Simple All-Microwave Entangling Gate for Fixed-Frequency Superconducting Qubits". Physical Review Letters. 107 (8): 080502. arXiv:1106.0553. Bibcode:2011PhRvL.107h0502C. doi:10.1103/PhysRevLett.107.080502. PMID 21929152. S2CID 9302474.
^ ^a ^b Gambetta, Jay M.; Chow, Jerry M.; Steffen, Matthias (13 January 2017). "Building logical qubits in a superconducting quantum computing system". npj Quantum Information. 3 (1): 2. arXiv:1510.04375. Bibcode:2017npjQI...3....2G. doi:10.1038/s41534-016-0004-0.
^ Blais, Alexandre; Huang, Ren-Shou; Wallraff, Andreas; Girvin, Steven; Schoelkopf, Robert (2004). "Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation". Phys. Rev. A. 69 (6): 062320. arXiv:cond-mat/0402216. Bibcode:2004PhRvA..69f2320B. doi:10.1103/PhysRevA.69.062320. S2CID 20427333.
^ ^a ^b ^c ^d ^e ^f DiVincenzo, David (February 1, 2008). "The Physical Implementation of Quantum Computation". IBM T.J. Watson Research Center. 48 (9–11): 771–783. arXiv:quant-ph/0002077. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID 15439711.
^ Devoret, M. H.; Schoelkopf, R. J. (7 March 2013). "Superconducting Circuits for Quantum Information: An Outlook". Science. 339 (6124): 1169–1174. Bibcode:2013Sci...339.1169D. doi:10.1126/science.1231930. PMID 23471399. S2CID 10123022.
^ Chow, Jerry M.; Gambetta, Jay M.; Córcoles, A. D.; Merkel, Seth T.; Smolin, John A.; Rigetti, Chad; Poletto, S.; Keefe, George A.; Rothwell, Mary B.; Rozen, J. R.; Ketchen, Mark B.; Steffen, M. (9 August 2012). "Universal Quantum Gate Set Approaching Fault-Tolerant Thresholds with Superconducting Qubits". Physical Review Letters. 109 (6): 060501. arXiv:1202.5344. Bibcode:2012PhRvL.109f0501C. doi:10.1103/PhysRevLett.109.060501. PMID 23006254. S2CID 39874288.
^ Niskanen, A. O.; Harrabi, K.; Yoshihara, F.; Nakamura, Y.; Lloyd, S.; Tsai, J. S. (4 May 2007). "Quantum Coherent Tunable Coupling of Superconducting Qubits". Science. 316 (5825): 723–726. Bibcode:2007Sci...316..723N. doi:10.1126/science.1141324. PMID 17478714. S2CID 43175104.
^ Morsch, Oliver; Zurich, E. T. H. "Quantum transfer at the push of a button". phys.org. Retrieved 2022-12-09.
^ ^a ^b Qiskit (2022-09-28). "How The First Superconducting Qubit Changed Quantum Computing Forever". Qiskit. Retrieved 2022-12-13.
^ Nakamura, Y.; Pashkin, Yu A.; Tsai, J. S. (April 1999). "Coherent control of macroscopic quantum states in a single-Cooper-pair box". Nature. 398 (6730): 786–788. arXiv:cond-mat/9904003. Bibcode:1999Natur.398..786N. doi:10.1038/19718. ISSN 0028-0836. S2CID 4392755.
^ "Baidu Releases Superconducting Quantum Computer and World's First All-Platform Integration Solution, Making Quantum Computing Within Reach". www.prnewswire.com (Press release). Retrieved 2022-12-13.
^ ^a ^b ^c ^d ^e "IBM Quantum roadmap to build quantum-centric supercomputers". IBM Research Blog. 2021-02-09. Retrieved 2022-12-13.
^ Lardinois, Frederic (2022-11-09). "IBM unveils its 433 qubit Osprey quantum computer". TechCrunch. Retrieved 2022-12-13.
^ "Our quantum computing journey". Google Quantum AI. Retrieved 2022-12-13.

외부 링크

IBM Quantum은 20개 이상의 양자 컴퓨터 시스템을 이용할 수 있습니다.
IBM Quantum Experience는 5 큐비트 양자 컴퓨터에서 양자 알고리즘을 작성하고 실행할 수 있는 무료 접근권을 제공합니다.
IBM의 퀀텀 컴퓨팅 로드맵은 2020년에 사용 가능한 65 큐비트 시스템과 2021년에 사용 가능한 127 큐비트 시스템을 보여줍니다.

[docs.pennylane.ai-1] ^ ^a ^b ^c ^d ^e ^f "PennyLane Documentation — PennyLane". docs.pennylane.ai. Retrieved 2022-12-11.

[2] Castelvecchi, Davide (5 January 2017). "Quantum computers ready to leap out of the lab in 2017". Nature. 541 (7635): 9–10. Bibcode:2017Natur.541....9C. doi:10.1038/541009a. PMID 28054624. S2CID 4447373.

[IBM-3] "IBM Makes Quantum Computing Available on IBM Cloud". www-03.ibm.com. 4 May 2016.

[4] "Imec enters the race to unleash quantum computing with silicon qubits". www.imec-int.com. Retrieved 2019-11-10.

[5] 콜마 라이언, 블레이크 R.존슨, 디에고 리스테, 브라이언 도노반, 토마스 A.Ohki, "동적 양자 컴퓨팅을 위한 하드웨어", arXiv:1704.08314v1

[6] "Rigetti Launches Quantum Cloud Services, Announces $1Million Challenge". HPCwire. 2018-09-07. Retrieved 2018-09-16.

[7] "Intel Invests US$50 Million to Advance Quantum Computing Intel Newsroom". Intel Newsroom.

[8] Kelly, J.; Barends, R.; Fowler, A. G.; Megrant, A.; Jeffrey, E.; White, T. C.; Sank, D.; Mutus, J. Y.; Campbell, B.; Chen, Yu; Chen, Z.; Chiaro, B.; Dunsworth, A.; Hoi, I.-C.; Neill, C.; O’Malley, P. J. J.; Quintana, C.; Roushan, P.; Vainsencher, A.; Wenner, J.; Cleland, A. N.; Martinis, John M. (4 March 2015). "State preservation by repetitive error detection in a superconducting quantum circuit". Nature. 519 (7541): 66–69. arXiv:1411.7403. Bibcode:2015Natur.519...66K. doi:10.1038/nature14270. PMID 25739628. S2CID 3032369.

[9] Arute, Frank; Arya, Kunal; Babbush, Ryan; Bacon, Dave; Bardin, Joseph C.; Barends, Rami; Biswas, Rupak; Boixo, Sergio; Brandao, Fernando G. S. L.; Buell, David A.; Burkett, Brian; Chen, Yu; Chen, Zijun; Chiaro, Ben; Collins, Roberto; Courtney, William; Dunsworth, Andrew; Farhi, Edward; Foxen, Brooks; Fowler, Austin; Gidney, Craig; Giustina, Marissa; Graff, Rob; Guerin, Keith; Habegger, Steve; Harrigan, Matthew P.; Hartmann, Michael J.; Ho, Alan; Hoffmann, Markus; Huang, Trent; Humble, Travis S.; Isakov, Sergei V.; Jeffrey, Evan; Jiang, Zhang; Kafri, Dvir; Kechedzhi, Kostyantyn; Kelly, Julian; Klimov, Paul V.; Knysh, Sergey; Korotkov, Alexander; Kostritsa, Fedor; Landhuis, David; Lindmark, Mike; Lucero, Erik; Lyakh, Dmitry; Mandrà, Salvatore; McClean, Jarrod R.; McEwen, Matthew; Megrant, Anthony; Mi, Xiao; Michielsen, Kristel; Mohseni, Masoud; Mutus, Josh; Naaman, Ofer; Neeley, Matthew; Neill, Charles; Niu, Murphy Yuezhen; Ostby, Eric; Petukhov, Andre; Platt, John C.; Quintana, Chris; Rieffel, Eleanor G.; Roushan, Pedram; Rubin, Nicholas C.; Sank, Daniel; Satzinger, Kevin J.; Smelyanskiy, Vadim; Sung, Kevin J.; Trevithick, Matthew D.; Vainsencher, Amit; Villalonga, Benjamin; White, Theodore; Yao, Z. Jamie; Yeh, Ping; Zalcman, Adam; Neven, Hartmut; Martinis, John M. (October 2019). "Quantum supremacy using a programmable superconducting processor". Nature. 574 (7779): 505–510. arXiv:1910.11333. Bibcode:2019Natur.574..505A. doi:10.1038/s41586-019-1666-5. PMID 31645734.

[10] Dayal, Geeta. "LEGO Turing Machine Is Simple, Yet Sublime". WIRED.

[qc-at-davis.github.io-11] "DiVincenzo's Criteria - Quantum Computing Codex". qc-at-davis.github.io. Retrieved 2022-12-13.

[pennylane.ai-12] Ballon, Alvaro (22 March 2022). "Quantum computing with superconducting qubits — PennyLane". Pennylane Demos. Retrieved 2022-12-13.

[13] "Cooper Pairs".{{cite web}}: CS1 유지 : url-status (링크)

[14] Shen, L. Y. L. (1972-02-01). "Superconductivity of Tantalum, Niobium and Lanthanum Studied by Electron Tunneling: Problems of Surface Contamination". AIP Conference Proceedings. 4 (1): 31–44. Bibcode:1972AIPC....4...31S. doi:10.1063/1.2946195. ISSN 0094-243X.

[15] Greicius, Tony (2020-06-12). "NASA's Cold Atom Lab Takes One Giant Leap for Quantum Science". NASA. Retrieved 2022-12-11.

[Kjaergaard-2020-16] Kjaergaard, Morten; Schwartz, Mollie E.; Braumüller, Jochen; Krantz, Philip; Wang, Joel I.-Jan; Gustavsson, Simon; Oliver, William D. (2020-03-10). "Superconducting Qubits: Current State of Play". Annual Review of Condensed Matter Physics. 11 (1): 369–395. arXiv:1905.13641. Bibcode:2020ARCMP..11..369K. doi:10.1146/annurev-conmatphys-031119-050605. ISSN 1947-5454. S2CID 173188891.

[17] Manucharyan, V. E.; Koch, J.; Glazman, L. I.; Devoret, M. H. (1 October 2009). "Fluxonium: Single Cooper-Pair Circuit Free of Charge Offsets". Science. 326 (5949): 113–116. arXiv:0906.0831. Bibcode:2009Sci...326..113M. doi:10.1126/science.1175552. PMID 19797655. S2CID 17645288.

[18] Houck, A. A.; Koch, Jens; Devoret, M. H.; Girvin, S. M.; Schoelkopf, R. J. (11 February 2009). "Life after charge noise: recent results with transmon qubits". Quantum Information Processing. 8 (2–3): 105–115. arXiv:0812.1865. doi:10.1007/s11128-009-0100-6. S2CID 27305073.

[19] Barends, R.; Kelly, J.; Megrant, A.; Sank, D.; Jeffrey, E.; Chen, Y.; Yin, Y.; Chiaro, B.; Mutus, J.; Neill, C.; O’Malley, P.; Roushan, P.; Wenner, J.; White, T. C.; Cleland, A. N.; Martinis, John M. (22 August 2013). "Coherent Josephson Qubit Suitable for Scalable Quantum Integrated Circuits". Physical Review Letters. 111 (8): 080502. arXiv:1304.2322. Bibcode:2013PhRvL.111h0502B. doi:10.1103/PhysRevLett.111.080502. PMID 24010421. S2CID 27081288.

[20] Metcalfe, M.; Boaknin, E.; Manucharyan, V.; Vijay, R.; Siddiqi, I.; Rigetti, C.; Frunzio, L.; Schoelkopf, R. J.; Devoret, M. H. (21 November 2007). "Measuring the decoherence of a quantronium qubit with the cavity bifurcation amplifier". Physical Review B. 76 (17): 174516. arXiv:0706.0765. Bibcode:2007PhRvB..76q4516M. doi:10.1103/PhysRevB.76.174516. S2CID 19088840.

[Martinis-2004-21] Martinis, John M.; Osborne, Kevin (2004-02-16). "Superconducting Qubits and the Physics of Josephson Junctions". arXiv:cond-mat/0402415. Bibcode:2004cond.mat..2415M. {{cite journal}}:저널 요구사항 인용 journal=(도움말)

[Hyyppä-2022-22] Hyyppä, Eric; Kundu, Suman; Chan, Chun Fai; Gunyhó, András; Hotari, Juho; Janzso, David; Juliusson, Kristinn; Kiuru, Olavi; Kotilahti, Janne; Landra, Alessandro; Liu, Wei; Marxer, Fabian; Mäkinen, Akseli; Orgiazzi, Jean-Luc; Palma, Mario (2022-11-12). "Unimon qubit". Nature Communications. 13 (1): 6895. arXiv:2203.05896. Bibcode:2022NatCo..13.6895H. doi:10.1038/s41467-022-34614-w. ISSN 2041-1723. PMC 9653402. PMID 36371435.

[Cottet_6383-23] Cottet, Nathanaël; Xiong, Haonan; Nguyen, Long B.; Lin, Yen-Hsiang; Manucharyan, Vladimir E. (2021-11-04). "Electron shelving of a superconducting artificial atom". Nature Communications. 12 (1): 6383. arXiv:2008.02423. Bibcode:2021NatCo..12.6383C. doi:10.1038/s41467-021-26686-x. ISSN 2041-1723. PMC 8569191. PMID 34737313.

[Nguyen-2019-24] Nguyen, Long B.; Lin, Yen-Hsiang; Somoroff, Aaron; Mencia, Raymond; Grabon, Nicholas; Manucharyan, Vladimir E. (2019-11-25). "High-Coherence Fluxonium Qubit". Physical Review X. 9 (4): 041041. arXiv:1810.11006. Bibcode:2019PhRvX...9d1041N. doi:10.1103/PhysRevX.9.041041. ISSN 2160-3308. S2CID 53499609.

[25] Science, The National University of; MISIS, Technology. "Fluxonium qubits bring the creation of a quantum computer closer". phys.org. Retrieved 2022-12-12.

[26] "Superconducting qubits – on islands, charge qubits and the transmon". LeftAsExercise. 2019-06-06. Retrieved 2022-12-12.

[27] Wendin, G. (2017-10-01). "Quantum information processing with superconducting circuits: a review". Reports on Progress in Physics. 80 (10): 106001. arXiv:1610.02208. Bibcode:2017RPPh...80j6001W. doi:10.1088/1361-6633/aa7e1a. ISSN 0034-4885. PMID 28682303. S2CID 3940479.

[28] Gambetta, J. M.; Chow, J. M.; Steffen, M. (2017). "Building logical qubits in a superconducting quantum computing system". npj Quantum Information. 3 (1): 2. arXiv:1510.04375. Bibcode:2017npjQI...3....2G. doi:10.1038/s41534-016-0004-0.

[29] Roth, Thomas E.; Ma, Ruichao; Chew, Weng C. (2021-06-21). "An Introduction to the Transmon Qubit for Electromagnetic Engineers". arXiv:2106.11352. {{cite journal}}:저널 요구사항 인용 journal=(도움말)

[30] Kjaergaard, Morten; Schwartz, Mollie E.; Braumüller, Jochen; Krantz, Philip; Wang, Joel I.-J.; Gustavsson, Simon; Oliver, William D. (2020-03-10). "Superconducting Qubits: Current State of Play". Annual Review of Condensed Matter Physics. 11 (1): 369–395. arXiv:1905.13641. Bibcode:2020ARCMP..11..369K. doi:10.1146/annurev-conmatphys-031119-050605. ISSN 1947-5454. S2CID 173188891.

[31] Shim, Yun-Pil; Tahan, Charles (2016-03-17). "Semiconductor-inspired design principles for superconducting quantum computing". Nature Communications. 7 (1): 11059. arXiv:1507.07923. Bibcode:2016NatCo...711059S. doi:10.1038/ncomms11059. ISSN 2041-1723. PMC 4800439. PMID 26983379.

[32] Wang, Chenlu; Li, Xuegang; Xu, Huikai; Li, Zhiyuan; Wang, Junhua; Yang, Zhen; Mi, Zhenyu; Liang, Xuehui; Su, Tang; Yang, Chuhong; Wang, Guangyue; Wang, Wenyan; Li, Yongchao; Chen, Mo; Li, Chengyao (2022-01-13). "Towards practical quantum computers: transmon qubit with a lifetime approaching 0.5 milliseconds". npj Quantum Information. 8 (1): 3. arXiv:2105.09890. Bibcode:2022npjQI...8....3W. doi:10.1038/s41534-021-00510-2. ISSN 2056-6387. S2CID 245950831.

[33] "Fig. 1: Unimon qubit and its measurement setup. Nature Communications". {{cite journal}}:저널 요구사항 인용 journal=(도움말)

[34] "Unimon: A new qubit to boost quantum computers from IQM IQM". www.meetiqm.com. Retrieved 2022-12-12.

[Buchanan-2022-35] Buchanan, Mark (2022-12-08). "Meet the Unimon, the New Qubit on the Block". Physics. 15: 191. Bibcode:2022PhyOJ..15..191B. doi:10.1103/Physics.15.191. S2CID 257514449.

[ShortRev-36] Devoret, M. H.; Wallraff, A.; Martinis, J. M. (6 November 2004). "Superconducting Qubits: A Short Review". arXiv:cond-mat/0411174.

[oneQBgate-37] Motzoi, F.; Gambetta, J. M.; Rebentrost, P.; Wilhelm, F. K. (8 September 2009). "Simple Pulses for Elimination of Leakage in Weakly Nonlinear Qubits". Physical Review Letters. 103 (11): 110501. arXiv:0901.0534. Bibcode:2009PhRvL.103k0501M. doi:10.1103/PhysRevLett.103.110501. PMID 19792356. S2CID 7288207.

[38] Chuang, Michael A. Nielsen & Isaac L. (2010). Quantum computation and quantum information (10th anniversary ed.). Cambridge: Cambridge University Press. pp. 174–176. ISBN 978-1-107-00217-3.

[39] Rigetti, Chad Tyler (2009). Quantum gates for superconducting qubits. p. 21. Bibcode:2009PhDT........50R. ISBN 9781109198874.

[Khazali-2020-40] Khazali, Mohammadsadegh; Mølmer, Klaus (2020-06-11). "Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits". Physical Review X. 10 (2): 021054. arXiv:2006.07035. Bibcode:2020PhRvX..10b1054K. doi:10.1103/PhysRevX.10.021054. ISSN 2160-3308.

[CRgate-41] Chow, Jerry M.; Córcoles, A. D.; Gambetta, Jay M.; Rigetti, Chad; Johnson, B. R.; Smolin, John A.; Rozen, J. R.; Keefe, George A.; Rothwell, Mary B.; Ketchen, Mark B.; Steffen, M. (17 August 2011). "Simple All-Microwave Entangling Gate for Fixed-Frequency Superconducting Qubits". Physical Review Letters. 107 (8): 080502. arXiv:1106.0553. Bibcode:2011PhRvL.107h0502C. doi:10.1103/PhysRevLett.107.080502. PMID 21929152. S2CID 9302474.

[NatRev2017-42] Gambetta, Jay M.; Chow, Jerry M.; Steffen, Matthias (13 January 2017). "Building logical qubits in a superconducting quantum computing system". npj Quantum Information. 3 (1): 2. arXiv:1510.04375. Bibcode:2017npjQI...3....2G. doi:10.1038/s41534-016-0004-0.

[Dispersive_Readout-43] Blais, Alexandre; Huang, Ren-Shou; Wallraff, Andreas; Girvin, Steven; Schoelkopf, Robert (2004). "Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation". Phys. Rev. A. 69 (6): 062320. arXiv:cond-mat/0402216. Bibcode:2004PhRvA..69f2320B. doi:10.1103/PhysRevA.69.062320. S2CID 20427333.

[DiVincenzo-2008-44] ^ ^a ^b ^c ^d ^e ^f DiVincenzo, David (February 1, 2008). "The Physical Implementation of Quantum Computation". IBM T.J. Watson Research Center. 48 (9–11): 771–783. arXiv:quant-ph/0002077. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. S2CID 15439711.

[45] Devoret, M. H.; Schoelkopf, R. J. (7 March 2013). "Superconducting Circuits for Quantum Information: An Outlook". Science. 339 (6124): 1169–1174. Bibcode:2013Sci...339.1169D. doi:10.1126/science.1231930. PMID 23471399. S2CID 10123022.

[46] Chow, Jerry M.; Gambetta, Jay M.; Córcoles, A. D.; Merkel, Seth T.; Smolin, John A.; Rigetti, Chad; Poletto, S.; Keefe, George A.; Rothwell, Mary B.; Rozen, J. R.; Ketchen, Mark B.; Steffen, M. (9 August 2012). "Universal Quantum Gate Set Approaching Fault-Tolerant Thresholds with Superconducting Qubits". Physical Review Letters. 109 (6): 060501. arXiv:1202.5344. Bibcode:2012PhRvL.109f0501C. doi:10.1103/PhysRevLett.109.060501. PMID 23006254. S2CID 39874288.

[47] Niskanen, A. O.; Harrabi, K.; Yoshihara, F.; Nakamura, Y.; Lloyd, S.; Tsai, J. S. (4 May 2007). "Quantum Coherent Tunable Coupling of Superconducting Qubits". Science. 316 (5825): 723–726. Bibcode:2007Sci...316..723N. doi:10.1126/science.1141324. PMID 17478714. S2CID 43175104.

[48] Morsch, Oliver; Zurich, E. T. H. "Quantum transfer at the push of a button". phys.org. Retrieved 2022-12-09.

[Qiskit-49] Qiskit (2022-09-28). "How The First Superconducting Qubit Changed Quantum Computing Forever". Qiskit. Retrieved 2022-12-13.

[50] Nakamura, Y.; Pashkin, Yu A.; Tsai, J. S. (April 1999). "Coherent control of macroscopic quantum states in a single-Cooper-pair box". Nature. 398 (6730): 786–788. arXiv:cond-mat/9904003. Bibcode:1999Natur.398..786N. doi:10.1038/19718. ISSN 0028-0836. S2CID 4392755.

[51] "Baidu Releases Superconducting Quantum Computer and World's First All-Platform Integration Solution, Making Quantum Computing Within Reach". www.prnewswire.com (Press release). Retrieved 2022-12-13.

[IBM_Research_Blog-2021-52] "IBM Quantum roadmap to build quantum-centric supercomputers". IBM Research Blog. 2021-02-09. Retrieved 2022-12-13.

[53] Lardinois, Frederic (2022-11-09). "IBM unveils its 433 qubit Osprey quantum computer". TechCrunch. Retrieved 2022-12-13.

[54] "Our quantum computing journey". Google Quantum AI. Retrieved 2022-12-13.

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[25]

[24]

[26]

[27]

[28]

[29]

[30]

[1]

[31]

[32]

[33]

[34]

[35]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

Search