피타고라스나무(프랙탈)

피타고라스 나무는 정사각형으로 만들어진 평면 프랙탈이다.네덜란드 수학 교사 알버트 E에 의해 발명되었습니다.1942년,^[1] 이것은 고대 그리스의 수학자 피타고라스의 이름을 따서 붙여진 것인데, 이는 전통적으로 피타고라스의 정리를 묘사하기 위해 사용된 구성에서 각각의 세 개의 정사각형이 직각 삼각형을 둘러싸고 있기 때문이다.가장 큰 정사각형의 크기가 L × L이면 피타고라스 나무 전체가 6L × 4L ^[2][3]크기의 상자 안에 딱 들어맞는다.트리의 미세한 디테일은 Levy C 곡선과 유사합니다.

건설

피타고라스 나무의 건축은 정사각형으로 시작한다.이 정사각형 위에 정사각형의 모서리가 쌍으로 일치하도록 각각 θ2/2의 선형 계수로 축소된 두 개의 정사각형이 구성됩니다.그런 다음 동일한 절차가 두 개의 작은 정사각형 ad ininitum에 재귀적으로 적용됩니다.아래 그림은 시공 프로세스의 ^[2][3]처음 몇 번의 반복을 보여줍니다.

오더 0	주문 1	주문 2	주문 3

이것은 가장 단순한 대칭 삼각형입니다.또는 삼각형의 변은 재귀적으로 동일한 비율로 되어 변은 역금비의 제곱근에 비례하고 정사각형의 면적은 황금비율에 비례한다.

지역

구조에서 반복 n은 영역 ${\displaystyle \frac{{\mathrm{}}^{}}{}}$ $(\$의 정사각형 2개를ⁿ 추가하여 총 면적 1을 추가합니다.따라서 트리의 면적은 한계 내에서 n → ∞로 제한 없이 커지는 것처럼 보일 수 있다.그러나 일부 사각형은 5차 반복부터 겹치고 트리는 6×4 ^[2]상자 안에 들어가므로 실제로는 면적이 한정되어 있습니다.

피타고라스 나무의 영역 A는 5 < A < 18 범위에 있어야 하며, 이는 추가 노력으로 더 좁혀질 수 있다.A의 실제 가치에 대해서는 거의 알려지지 않은 것 같습니다.

각도 변경

이등변형의 흥미로운 집합은 이등변삼각형을 유지하되 기준각(표준 피타고라스 나무의 경우 90도)을 변경함으로써 구성할 수 있다.특히 베이스 반각을 (30°) = 아크신(0.5)으로 설정하면 정사각형의 크기가 일정함을 쉽게 알 수 있다.첫 번째 오버랩은 네 번째 반복에서 발생합니다.생성되는 일반적인 패턴은 구성 정사각형으로 둘러싸인 육각형 배열인 롬비트릭사각형 타일링입니다.

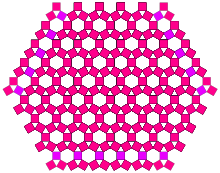주문 4	주문 10

반각도가 90도인 한계에서는 겹치는 부분이 없고, 총 면적이 베이스 정사각형 면적의 2배입니다.기본 반각 값과 정사각형이 처음 겹치는 반복 사이에 알고리즘 관계가 있는지 알아보는 것이 흥미로울 것입니다.

역사

피타고라스 나무는 Albert E에 의해 처음 지어졌다.1942년 ^[2][4]네덜란드 수학 교사 보스만(1891-1961년.

「 」를 참조해 주세요.

• 레비 C 곡선

레퍼런스

외부 링크

• 피타고라스 미술관
• 코드가 있는 인터랙티브 제너레이터
• "Pythagoras tree with different geometries as well as in 3D". Archived from the original on 2008-01-15.
• 에릭 W의 프로그램을 바탕으로 한 엔리케 젤레니 감독의 피타고라스 나무. Weisstein, Wolfram 데모 프로젝트.
• Weisstein, Eric W. "Pythagoras Tree". MathWorld.
• 3차원 피타고라스 나무
• 피타고라스 트리를 생성하는 MatLab 스크립트
• 가상현실 소프트웨어 Neotrie VR로 단계별 구축
• Pourahmadazar, J.; Ghobadi, C.; Nourinia, J. (2011). "Novel Modified Pythagorean Tree Fractal Monopole Antennas for UWB Applications". IEEE Antennas and Wireless Propagation Letters. New York: IEEE. 10: 484–487. Bibcode:2011IAWPL..10..484P. doi:10.1109/LAWP.2011.2154354.