런케이티드 120셀

사행성

120 셀	런케이티드 120 셀 (120셀 확장)	120셀의 회전 속도
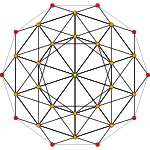600셀	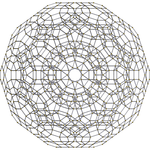런시트드 600 셀	잡티트런 120 셀
H3 Coxeter 평면의 직교 투영

4차원 기하학에서 런케이티드 120 셀(또는 런케이티드 600 셀)은 볼록한 균일한 4 폴리토프로서 일반 120 셀의 런케이닝(제3차 잘림)이다.

120개의 셀에는 순열 자르기와 운율을 포함하여 4도의 운율이 있다.

런케이티드 120 셀은 일반 4 폴리토프, 즉 120 셀 또는 600 셀에 적용되는 팽창으로 볼 수 있다.

런케이티드 120 셀

런케이티드 120 셀
유형	제복4폴리토프
균일지수	38
콕시터 다이어그램
세포	2640 총계: 120 5.5.5 720 4.4.5 1200 4.4.3 600 3.3.3
얼굴	7440: 2400{3}+3600{4}+ 1440{5}
가장자리	7200
정점	2400
정점수	등삼각형 항정신병균
슐레플리 기호	t0,3{5,3,3}
대칭군	H4, [3,3,5], 14400 주문
특성.	볼록하게 하다

룬케이트 120셀 또는 작은 디스프리스마토헥사코시케카토소노사초론은 균일한 4폴리토프다.도데카헤드라 120개, 오각 프리즘 720개, 삼각 프리즘 1200개, 테트라헤드라 600개 등 2640개의 세포를 가지고 있다.그것의 꼭지점은 균일하지 않은 삼각형 항정신병(등방삼각형 항정신병)으로, 그것의 밑부분은 도데면체와 사면체를 나타내며, 측면은 3개의 삼각형 프리즘과 3개의 오각형 프리즘을 나타낸다.

대체 이름

• 런케이트 120 셀 / 런케이트 600 셀 (노먼 W. 존슨)
  • 런케티드 헤카토닉오사초론 / 런케티드 도데카콘타초론 / 런케티드 헥사코시초론 / 런케티드 폴리도데카헤드론 / 런케티드 폴리테트라헤드론
• 스몰디프리스마토헥사코시카토노사초론(아크로니마:sidpixhi) (조지 올셰프스키, 조나단 바우어스)^[1]

이미지들

Schlegel 다이어그램(그림에 4면체 세포만 표시됨)

다면 고리

5배축 셀

3배축 셀

2배축 셀

Coxeter 평면의 직교 투영

H3

A2/B3

A3/B2

120셀의 회전 속도

120셀의 회전 속도
유형	제복4폴리토프
균일지수	43
콕시터 다이어그램
세포	2640 총계: 120 (3.10.10) 720 (4.4.10) 1200 (3.4.4) 600 (3.4.3.4)
얼굴	13440: 4800{3}+7200{4}+ 1440{10}
가장자리	18000
정점	7200
정점수	불규칙 직사각형 피라미드
슐레플리 기호	t0,1,3{5,3,3}
대칭군	H4, [3,3,5], 14400 주문
특성.	볼록하게 하다

120셀 또는 프리즘토사혼방 헥사코시초롱은 균일한 4폴리토프다.잘린 도데카헤드라 120개, 십이각 프리즘 720개, 삼각 프리즘 1200개, 큐보타헤드라 600개 등 2640개의 세포를 담고 있다.그것의 꼭지점은 불규칙한 직사각형 피라미드인데, 잘린 도데면체 1개, 십각형 프리즘 2개, 삼각형 프리즘 1개, 큐옥타면체 1개가 있다.

대체 이름

• 룬시칸텔레이트 600셀(노르만 W. 존슨)
• 프리즘atorhombated 헥사코시초론 (Acronim: pric) (George Olshevsky, Jonathan Bowers)^[2]

이미지들

슐레겔 도표(삼각형 프리즘만 표시됨) Coxeter 평면의 직교 투영

H3

A2/B3

A3/B2

런시트드 600 셀

런시트드 600 셀
유형	제복4폴리토프
균일지수	44
콕시터 다이어그램
세포	2640 총계: 120 3.4.5.4 720 4.4.5 1200 4.4.6 600 3.6.6
얼굴	13440: 2400{3}+7200{4}+ 1440{5}+2400{6}
가장자리	18000
정점	7200
정점수	사다리꼴 피라미드
슐레플리 기호	t0,1,3{3,3,5}
대칭군	H4, [3,3,5], 14400 주문
특성.	볼록하게 하다

600셀 또는 프리즘토좀비 헤카토노사초론은 균일한 4폴리토프다.그것은 2640개의 세포로 구성되어 있다: 120개의 롬비코시도데카헤드론, 600개의 잘린 테트라헤드라, 720개의 오각형 프리즘, 1200개의 육각 프리즘.7200정점, 18000엣지, 13440면(2400 삼각형, 7200제곱, 2400헥사곤)을 가지고 있다.

대체 이름

• Runcicantellated 120-cell (Norman W. Johnson)
• 프리즘토호몬드헤카토노사초론(아크로니임:프라히) (조지 올셰프스키, 조나단 바우어스)^[3]

이미지들

슐레겔 도표

Coxeter 평면의 직교 투영

H3

A2/B3

A3/B2

잡티트런 120 셀

잡티트런 120 셀
유형	제복4폴리토프
균일지수	46
콕시터 다이어그램
세포	2640 총계: 120 4.6.10 720 4.4.10 1200 4.4.6 600 4.6.6
얼굴	17040 총계: 10800 {4}, 4800 {6} 1440 {10}
가장자리	28800
정점	14400
정점수	치랄 스칼렌 사면체
슐레플리 기호	t0,1,2,3{3,3,5}
대칭군	H4, [3,3,5], 14400 주문
특성.	볼록하게 하다

전분 120셀 또는 대 디프리스마토헥사코시카토소나초론은 볼록한 제복 4폴리토프로, 잘린 이코시도데카헤드라 120셀, 잘린 옥타헤드라 600자, 720 십각형 프리즘, 그리고 1200 육각형 프리즘으로 구성되어 있다.정점 14400, 가장자리 28800, 면 17040(사각형 10800, 육각 4800, 데카곤 1440)을 가지고 있다.비프리즘 볼록한 제복 4폴리토프 중 가장 크다.

정점과 가장자리는 Coxeter 그룹 H의₄ Cayley 그래프를 형성한다.

대체 이름

• 옴니트런 120셀 / 옴니트런 600셀 (노먼 W. 존슨)
• 옴니트런하트론 / 옴니트런하트 헥사코시초론 / 옴니트런하드론 / 옴니트런하드 다면체
• 그레이트디프리스마토헥사코시카토노사초론(Acronim gidpixhi) (George Olshevsky, Jonathan Bowers)^[4]

이미지들

슐레겔 도표(잘린 이코시다데카헤드론 중심) (직교 보기, 십각형 프리즘 셀 중심)	입체 투영법 (잘린 이코시다데카헤드론 중심)

Coxeter 평면의 직교 투영

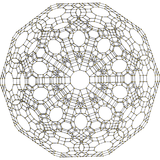H3

A2/B3

A3/B2

다면 고리

5배축 셀

3배축 셀

2배축 셀

그물

잡티트런 120 셀

듀얼에서 옴니트런으로 120셀

모델

3D 투영법으로서 최초의 완전한 물리학적 모델은 대니얼 더디와 데이비드 리히터가 이끄는 팀이 2006년 8월 9일 브리지스 컨퍼런스의 런던 지식 랩의 Zome 시스템을 사용하여 만들었다.^[5]

풀 스너브 120셀

전체 모욕 120-cell 또는omnisnub 120-cell,omnitruncated 120-cell의 교대로 정의되지만 그것과 1200년 octahedrons, 600icosahedrons, 720오각형의 antiprisms, 120스너브 dodecahedrons, 7200 장치를 삭제된에서 격차에서 생성된 Coxeter, 다이어그램과 대칭[5,3,3]+될 수 있게 만들 수 없다. v공권력9840개의 셀, 35040면, 32400개의 가장자리, 7200개의 꼭지점을 가지고 있다.^[6]

관련 폴리토페스

이러한 폴리탑은 H₄ 대칭이 있는 15개의 균일한 4폴리탑의 일부분이다.

H형4 폴리토페스
120 셀	수정한 120 셀	잘린 120 셀	알 수 있는 120 셀	녹이 슨 120 셀	칸트런이 있는 120 셀	구김살이 있는 120 셀	다량의 120 셀
{5,3,3}	r{5,3,3}	t{5,3,3}	rr{5,3,3}	t0,3{5,3,3}	tr{5,3,3}	t0,1,3{5,3,3}	t0,1,2,3{5,3,3}
600셀	수정한 600셀	잘린 600셀	알 수 있는 600셀	굵게 깎인 600셀	칸트런이 있는 600셀	구김살이 있는 600셀	다량의 600셀
{3,3,5}	r{3,3,5}	t{3,3,5}	rr{3,5}	2t{3,5}	tr{3,5}	t0,1,3{3,3,5}	t0,1,2,3{3,3,5}

메모들

참조

• 케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6
  • (용지 22) H.S.M. Coxeter, 정규 및 반정규 다항체 I, [수학]Zeit. 46 (1940) 380-407, MR 2,10]
  • (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559-591]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
• J.H.콘웨이와 M.J.T. 가이: 4차원 아르키메데스 폴리토페스, 코펜하겐에서의 볼록성에 관한 콜로키움의 진행, 1965년 38페이지/39페이지
• N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
• 4차원 아르키메데스 폴리토페스(독일어), 마르코 뮐러, 2004년 박사 논문 [1] m55 m62 m60 m64
• 헤카토노사초론(120셀)과 헥사코시초론(600셀)을 기반으로 한 볼록한 균일한 폴리초라 - 모델 38, 44, 47, 조지 올셰프스키.
• Klitzing, Richard. "4D uniform polytopes (polychora)". x3o3o5x - sidpixhi, x3o3x5x - free, x3x3o5x - prahi, x3x3x5x - gidpixhi

외부 링크

• H4 좌표가 있는 균일한 폴리탑: t03{5,3,3} t013{3,5} t013{5,3,3} t0123{5,3,3}

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	122 • 221
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	132 • 231 • 321
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	142 • 241 • 421
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1k2 • 2k1 • k21	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록