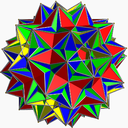
균일성 다면체
Uniform star polyhedron
기하학에서 획일적인 항성 다면체는 자가 교차하는 획일적인 다면체다.그것들은 때때로 자기 교차성을 의미하기 위해 비콘벡스 다면체라고도 불린다.각 다면체는 항성 다각형 면, 항성 다각형 정점 또는 둘 모두를 포함할 수 있다.
57개의 비프리즘적 균일성 다면체 전체 세트에는 케플러-푸인소트 다면체라 불리는 4개의 정규성, 5개의 준정형성, 48개의 반정형성체가 포함된다.
또한 두 가지 무한대의 균일한 항성 프리즘과 균일한 항성 항정신병 세트가 있다.
(비기생성)별 폴리곤(폴리곤 밀도가 1보다 큰)이 타일이 겹치는 원형 폴리곤에 해당하는 것처럼, 중심을 통과하지 않는 별 폴리테드라는 폴리토프 밀도가 1보다 크고, 타일이 겹치는 구형 폴리헤드라에 해당하며, 이와 같은 균일한 별 폴리헤드라가 47개 있다.나머지 10개의 비prism적 제복성별인 폴리헤드라는 중심을 통과하는 별은 밀러의 괴물은 물론 혈중합성형이며, 밀러의 밀도가 잘 규정되어 있지 않다.
비콘벡스 형태는 슈바르츠 삼각형으로 구성된다.
모든 균일한 다면체는 대칭 그룹에 의해 아래에 나열되고 정점 배열에 의해 분류된다.
일반 다면체에는 슐레플리 기호가 표시되어 있다.다른 비정규 균일 다면체는 정점 구성과 함께 나열된다.
추가적인 수치인 사이비 대 롬비쿠보톡타헤드론은 보통 일반 얼굴들로 구성되고 같은 정점을 가지고 있음에도 불구하고, 실제로는 균일한 별 폴리토프로 포함되지 않는다.
참고: 아래 비 컨벡스 형식의 경우 볼록한 선체 꼭지점 배열이 이들 중 하나와 위상은 같지만 얼굴이 비정규적일 때 추가 설명자 Nonuniform을 사용한다.예를 들어 균일하지 않은 수식어는 사각형이 아닌 가장자리 대신 직사각형을 만들 수 있다.
치측 대칭
프리즘 균일 다면체를 참조하십시오.
사면 대칭
4차 대칭(기본 영역 뫼비우스 삼각형(3 3 2)을 갖는 4차 대칭)인 비콘벡스형(nonvex) 형태가 있다.
독특한 비콘벡스 균일한 다면체를 생성하는 두 개의 슈바르츠 삼각형이 있는데, 바로 하나의 직각 삼각형이다.3/2 3 2), 그리고 하나의 일반 삼각형(3/2 3).일반 삼각형(3/2 3)은 완전한 팔면 대칭으로 주어지는 팔면체 대칭을 생성한다.
| 정점 배열 (콘벡스 선체) | 비콘벡스 양식 | |
|---|---|---|
 사면체 | ||
 수정사면체 팔면체 |  4.3⁄2.4.3 3⁄2 3 2 | |
 잘린 사면체 | ||
 캔텔레이트 사면체 (쿠보타헤드론) | ||
 만능경화사면체 (팔면체) | ||
 스너브 사면체 (아이코사헤드론) | ||
팔면 대칭
8개의 볼록형식이 있으며, 8각대칭이 있는 10개의 비콘벡스형(기본영역 뫼비우스 삼각형(4 3 2))이 있다.
비콘벡스형태를 생성하는 슈바르츠 삼각형 4개, 오른쪽 삼각형 2개(½ 4 2개), 그리고 일반삼각형 2개(½ 3 2개), 일반삼각형 2개: (4/3 4 3개), (3/2 4개)가 있다.
| 정점 배열 (콘벡스 선체) | 비콘벡스 양식 | ||
|---|---|---|---|
 큐브 | |||
 팔면체 | |||
 큐폭타헤드론 |  6.4⁄3.6.4 4⁄3 4 3 |  6.3⁄2.6.3 3⁄2 3 3 | |
 잘린 큐브 |  4.8⁄3.4⁄3.8⁄5 2 4⁄3 (3⁄24⁄2) |  8⁄3.3.8⁄3.4 3 4 4⁄3 |  4.3⁄2.4.4 3⁄2 4 2 |
 잘린 팔면체 | |||
 롬비큐옥타헤드론 |  4.8.4⁄3.8 2 4 (3⁄24⁄2) |  8.3⁄2.8.4 3⁄2 4 4 |  8⁄3.8⁄3.3 2 3 4⁄3 |
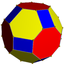 통일형 잘린 칸옥타헤드론 |  4.6.8⁄3 2 3 4⁄3 | ||
 통일형 잘린 칸옥타헤드론 |  8⁄3.6.8 3 4 4⁄3 | ||
 스너브 큐브 | |||
이코사면 대칭
이코사이드 대칭(기본 영역 뫼비우스 삼각형(5 3 2))을 가진 8개의 볼록 형태와 46개의 비콘벡스 형태가 있다.(또는 스킬링의 수치가 포함된 경우 47개의 비컨벡스 양식).비콘벡스 스너브 형태 중 일부는 반사 정점 대칭을 가지고 있다.
퇴보 사건
콕시터(Coxeter)는 와이토프(Wythoff) 공법으로 여러 개의 퇴행성 다면체를 확인했는데, 여기에는 겹치는 가장자리나 정점이 포함되어 있다.이러한 퇴보적인 형태는 다음과 같다.
스킬링의 몸매
또 다른 비콘벡스 퇴화성 다면체로는 대식성 다면체(disnub dirhombidodechahedron)가 있는데, 스킬링의 형상이라고도 알려져 있는데, 정점 균일하지만 우주에서 일치하는 가장자리 쌍을 가지고 있어 네 개의 얼굴이 어떤 가장자리에서 만난다.이중 가장자리가 있어 획일적인 다면체보다는 퇴보적인 획일적인 다면체로 계산된다.그것은h I 대칭을 가지고 있다.
참고 항목
참조
- Coxeter, H. S. M. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 246 (916): 401–450. doi:10.1098/rsta.1954.0003.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. OCLC 1738087.
- 브뤼크너, M. Vielekeke und Vielflache. 테오리와 게시히테..독일 라이프치히:티브너, 1900년[1]
- Sopov, S. P. (1970), "A proof of the completeness on the list of elementary homogeneous polyhedra", Ukrainskiui Geometricheskiui Sbornik (8): 139–156, MR 0326550
- Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 278: 111–135, doi:10.1098/rsta.1975.0022, ISSN 0080-4614, JSTOR 74475, MR 0365333
- 하엘, Z.균일 폴리헤드라, 기하학적 디디카타 47, 57-110, 1993.Zvi Har'El, Kaleido 소프트웨어, 이미지, 듀얼 이미지
- 메더, R. E. 제복 폴리헤드라1993년 Mathematica J. 3, 48-57.[2]
- Messer, Peter W. Closed-Forms for Uniform Polyedra and The Duals, 이산 & 계산 기하학 27:353-375(2002년)
- Klitzing, Richard. "3D uniform polyhedra".