정십이면체

정십이면체
(회전 모델을 보려면 여기를 클릭하십시오)
유형	아르키메데스 고체 고른 다면체
요소들	F = 92, E = 150, V = 60 (평균 = 2)
측면별 면	(20+60){3}+12{5}
콘웨이 표기법	sD
슐레플리 기호	sr{5,3} $또는{\displaystyle }$ s$}{$
	ht0,1,2{5,3}
위토프 기호	2 3 5
콕서터 다이어그램
대칭군	나는,1/2H3, [5,3],+ (532), 60 주문
회전군	I, [5,3],+ (532), 60 주문
이면각	3-3: 164°10′31″ (164.18°) 3-5: 152°55′53″ (152.93°)
레퍼런스	U29, C32, W18
특성.	반규칙 볼록 키랄
유색인 얼굴	3.3.3.3.5 (Vertex 그림)
오각육면체 (수직 다면체)	그물

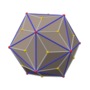
기하학에서, 스누브 십이면체 또는 스누브 십이면체는 두 가지 이상의 정다각형 면으로 구성된 13개의 볼록한 등각형의 비각형 다면체 중 하나인 아르키메데스의 다면체입니다.

정십이면체는 92개의 면을 가지고 있습니다: 12개는 오각형이고 나머지 80개는 정삼각형입니다.또한 150개의 모서리와 60개의 꼭짓점이 있습니다.

그것은 서로의 거울 이미지(또는 "반동형")인 두 가지 다른 형태를 가지고 있습니다.두 형태의 결합은 두 개의 작은 십이면체의 합성물이고, 두 형태의 볼록한 선체는 깎은 정이십이면체입니다.

케플러는 1619년에 그의 하모니쿠스 문디에서 그것을 12면체 시움으로 라틴어로 처음 이름 지었습니다.H. S. M. 콕서터는 수직으로 확장된 $슐레플리{\displaystyle }$ ${\displaystyle \begin{array}{}기호\\ \mathrm{}\end{array}}${53}({$displaystyle s\scriptstyle begin{Bmatrix}5\3\end${Bmatrix$})$와 평평한 슐레플리 기호 sr{5,3}를 사용하여 십이십이면체 또는 이십이십이면체라고 불리는 이십이체에서 동일하게 파생될 수 있다고 지적했습니다.

데카르트 좌표

γ 0.94315125924를 입방 다항식³ x + 2x² - γ의² 실제 0으로 하자, 여기서 γ는 황금비입니다.포인트 p를 다음과 같이 지정합니다.

${\displaystyle p}$ $=$ ( ${\displaystyle \begin{array}{c}{}^{}{}^{}\end{array}}$2 - ${\displaystyle \begin{array}{c}{}^{}\end{array}}$ 2${\displaystyle \begin{array}{}\\ \end{array}}$ξ - $ϕ$ 3${\displaystyle \begin{array}{c}{}^{}\end{array}}$+${\displaystyle \begin{array}{c}{}^{}\end{array}}$ + ${\displaystyle \begin{array}{c}2\end{array}}$ ${\displaystyle \begin{array}{c}{}^{}\\ \end{array}}$ 2${\displaystyle \begin{array}{}\end{array}}$ξ$$) \ $displaystyle$ p= begin {$pmatrix$$phi$^{$2}-\phi ^{2}-\phi$ \xi $\-\phi$ \xi $\{2}\xi$ \$endatrix}.$

회전 행렬₁ M과₂ M이 다음과 같이 주어지도록 하자.

$디스플레이 스타일 M_{1}={{pmatrix}{\frac{1}{2\phi}}&-{\frac{2}&{\frac{1}{2}&{\frac{2}}&{\frac{1}}{\frac{1}}{\frac{2}}{\frac{\frac{1}{\phi}}{\frac{\frac{\frac}{\frac{\frac{\frac{\frac{\frac}}}{\frac{\frac{\frac$

그리고.

${\displaystyle M_{2}=sysbegin{pmatrix}0&0&1\0&1\end{pmatrix}.}$

M은₁ 2θ/5의 각도를 시계 반대 방향으로 통과하는 축(0,1,θ) 주위의 회전을 나타내며₂, M은 (x,y,z)의 주기적 이동이 2θ/3의 각도를 통과하는 축(1,1,1) 주위의 회전을 나타냅니다.그런 다음 스누브 십이면체의 60개 꼭짓점은 수렴으로 반복되는 M 및/또는₂ M에₁ 의한 반복 곱셈 아래에 있는 점 p의 60개 이미지입니다.(M과₁ M₂ 행렬은 정이십면체의 60 회전 대칭에 해당하는 60 회전 행렬을 생성합니다.)꼭짓점의 좌표는 1, φ, ξ, φ², ξ², φ, ξ의 적분 선형 조합입니다.가장자리 길이가 같습니다.

$화면표시 스타일 2.449,750,618,41.}$

모든 좌표를 무효화하면 이 고르지 못한 십이십면체의 거울 이미지가 제공됩니다.

부피로서, 육면체는 80개의 삼각형과 12개의 오각형 피라미드로 구성되어 있습니다.삼각뿔 하나의 부피₃ V는 다음과 같이 주어진다:

${\displaystyle V_{3}=displayfrac{1}{3}}\phi \left(3\xi^{2}-\phi^{2}\right)\displaystyle 0.027\,274\,068\,85,}$

그리고 하나의 오각뿔의 부피₅ V는 다음과 같습니다.

${\displaystyle V_{5}=displayfrac {1}{3}}(3\phi +1)\left(\phi +3-xi -3\xi ^{2}\right)\xi ^{3}\xi ^{3}\displaystyle 0.103\lots\,665\,04.}$

총 볼륨은.

$디스플레이 스타일 80V_{3}+12V_{5}\approx 3.422\,121\,488\,76.}$

원주율은 다음과 같습니다.

$표시({style}{4\xi ^{2}-\phi ^{2}})\timeout 0.969\,589\,192\,65.}$

중위수는 π와 같습니다.이것은 ξ의 숫자에 대한 흥미로운 기하학적 해석을 제공합니다.위에서 설명한 정이십면체의 20개의 "이십면체" 삼각형은 정이십면체의 면과 동일 평면입니다.이 "구입된" 정이십면체의 중간 반지름은 1과 같습니다.이것은 π가 정십이면체의 중이십면체와 그것이 새겨진 정이십면체 사이의 비율이라는 것을 의미합니다.

삼각형-삼각형 이면각은 다음과 같이 주어진다.

${\displaystyle \theta _{33}=180^{\deta}-\arccos \lefts\frac {2}{3}}\xi +{\frac {1}{3}\right)\deta 164.175\,366\,056\,03^{\deta}$

삼각형-오각형 이면각은 다음과 같이 주어진다.

$디스플레이 스타일 \theta _{35}=180^{\delay}-\arccos {\sqrt {frac {-(4\phi +8)\xi ^{2}-(4\phi +8)\xi +12\phi +19}}\flay 152.929\,920\delay,84^{\delay}$

메트릭 속성

가장자리 길이가 1인 정십이면체의 경우, 표면적은

${\displaystyle A=20{\sqrt {3}}+3sqrt {25+10sqrt {5}}}\displaystyle 55.286\,744\,958\,445\,15.}$

그것의 부피는

$디스플레이 스타일 V=displayfrac {(3\phi +1)\xi ^{2}+(3\phi +1)\xi -\phi /6-2}{\sqrt {3\xi ^{2}-\phi ^{2}}\timeout 37.616\,649\962,733\36.}$

또는 이 볼륨은 다음과 같이 기록될 수 있습니다.

${\displaystyle V=sqfrac {5+5\dsqrt {5}}{6sqrt {3}}{\sqrt {18+6sqrt {5}}}+{a\leftsqrt {5}}\,{+}\,{a}\right)}}}+{\frac{5+3\sqrt{5}}}{24\sqrt{2}}}{\sqrt{72+{\sqrt{5}}}a\left\3+3\sqrt{5}}}\,{+}\rt}}}{\sqrt37.616\649\9,9,733,36,36,36}}}$

어디에,

${\displaystyle a=sqsqrt[{3}]{54(1+{\sqrt {5}})+6sqrt {102+sqrt {5}}}+{\sqrt[{3}}}}}-6sqrt {102+sqrt {5}}}}{\displaystyle 10.293},368,998\sqlotsqrt,21.}$

그것의 둘레는

${\displaystyle R=displayfrac {1}{2}}{\sqrt {\frac {2-\xi}{1-\xi}}\timeout 2.155\,837\,196.}$

그것의 중간 반경은

${\displaystyle r=novfrac {1}{2}}{\sqrt {\frac {1}{1-\xi}}\display2.097\,053\,835\,25.}$

두 개의 내접구가 있는데, 하나는 삼각형 면에 닿고, 하나는 약간 더 작은 오각형 면에 닿습니다.이들의 반지름은 각각 다음과 같습니다.

${\displaystyle r_{3}=displayfrac{phi{sqrt{3}}{6\xi}}{\sqrt{frac{1}{1-\xi}}\display2.077\,089\,659\,74}$

그리고.

${\displaystyle r_{5}={1}{2}}{\sqrt {{phi ^{2}}{\xi ^{2}+3\phi ^{2}\xi +{\frac {11}{5}}\phi +{{\frac {12}}}\frac 1.980,915\947,28.}$

R에서² 육방정식의 4개의 양의 실수근

$디스플레이 스타일 4096R^{12}-27648R^{10}+47104R^{8}-35776R^{6}+13872R^{4}-2696R^{2}+209=0}$

은 정십이면체(U₂₉)의 둘레 반지름, 대 정십이면체(U₅₇), 대 정십이면체(U), 대 역 정십이면체(U₆₉), 대 정십이면체(U₇₄)입니다.

편평한 십이십면체는 모든 아르키메데스 고체 중에서 가장 높은 구형도를 가지고 있습니다.만약 구형도가 표면적의 입방체에 대한 부피 제곱의 비율로 정의되고, 36θ의 상수(이 상수가 구면의 구형도를 1과 같게 함)를 곱하면, 구형도는 약 0.^[1]947입니다.

직교 투영법

스누브 십이면체는 아래와 같이₂ A 및 H 콕서터 평면에₂ 해당하는 두 가지 유형의 면(삼각형 및 오각형)을 중심으로 두 개의 특히 대칭적인 직교 투영을 가지고 있습니다.

직교 투영법

중심:	얼굴 삼각형	얼굴 펜타곤	가장자리
단단한
와이어프레임
프로젝티브 대칭성	[3]	[5]+	[2]
듀얼

기하학적 관계

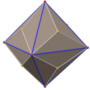
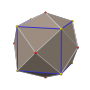
정십이면체는 십이면체의 오각형 면 12개를 바깥쪽으로 당겨서 더 이상 닿지 않게 함으로써 생성될 수 있습니다.적절한 거리에서 분할된 모서리 사이의 정사각형 면과 분할된 꼭짓점 사이의 삼각형 면을 채워 마름모꼴 십이면체를 만들 수 있습니다.그러나 스너브 양식의 경우 오각형 면을 약간 덜 밖으로 당기고 삼각형 면만 추가하고 다른 간격은 비워 둡니다(다른 간격은 이 점에서 직사각형입니다.그런 다음 오각형과 삼각형의 중심에 동일한 회전을 적용하여 간격을 두 개의 정삼각형으로 채울 수 있을 때까지 회전을 계속합니다.(누군가십이면체의 경우 면을 뽑는 적정량이 적다는 사실은 두 가지 방법 중 하나로 볼 수 있습니다: 누군가십이면체의 둘레 반지름이 이코십이면체의 둘레 반지름보다 작거나, 또는,분할된 꼭짓점에 의해 형성된 정삼각형의 모서리 길이는 오각형 면이 회전할 때 증가합니다.)

스너브 십이면체는 또한 교대 과정에 의해 깎은 정이십이면체에서 파생될 수 있습니다.깎은 정이십이면체의 꼭짓점 중 60개는 위상적으로 한 정이십이면체와 동등한 다면체를 형성하고, 나머지 60개는 거울상을 형성합니다.결과 다면체는 꼭짓점 전이적이지만 균일하지 않습니다.

또는 데카르트 좌표(위)에 의해 주어진 정십이면체의 꼭짓점과 거울을 결합하면 반규칙으로 깎은 정이십이면체가 됩니다.이 규칙적인 다면체와 반규칙적인 다면체의 비교는 오른쪽 그림에 나와 있습니다.

이 대안적인 정십이면체의 정점에 대한 데카르트 좌표는 12개의 집합(5개의 잘린 정십이면체 데카르트 좌표에 포함된 24개의 가능한 짝수 순열)을 선택하여 얻습니다.다음 세 집합에서 음수 기호가 홀수인 경우가 대체됩니다.

(±1/θ, ±1/θ, ±(3 + θ)),

(±1/θ, ±θ², ±(-1 + 3θ)),

(±θ, ±3, ±2θ),

짝수의 마이너스 기호는 다음과 같습니다.

(±2/θ, ±θ, ±(1 + 2θ)),

(±(2θ - 1), ±2, ±(2 + θ),

여기서 γ = 1 + γ 5/2는 황금비입니다.

관련 다면체 및 타일링

정이십면체 다면체 군
대칭: [5,3],(*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
이중에서 균일한 다면체까지
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

이 반정다면체는 꼭짓점 도형(3.3.3.3.n)과 콕서터-딘킨 다이어그램을 가진 반정다면체와 타일링의 시퀀스의 멤버입니다.이러한 수치와 쌍대칭은 (n32) 회전 대칭을 가지며, n = 6의 경우 유클리드 평면에 있고, 더 높은 n의 경우 쌍곡선 평면에 있습니다.열은 n = 2로 시작하며 한 집합의 면이 디곤으로 퇴화된 것으로 간주할 수 있습니다.

n32 스누빌링의 대칭 돌연변이: 3.3.3.3.n v t
대칭 n32	구면				유클리드	콤팩트 쌍곡선		파라콤프.
	232	332	432	532	632	732	832	∞32
스너브 수치
구성.	3.3.3.3.2	3.3.3.3.3	3.3.3.3.4	3.3.3.3.5	3.3.3.3.6	3.3.3.3.7	3.3.3.3.8	3.3.3.3.∞
자이로 수치
구성.	V3.3.3.3.2	V3.3.3.3.3	V3.3.3.3.4	V3.3.3.3.5	V3.3.3.3.6	V3.3.3.3.7	V3.3.3.3.8	V3.3.3.3.1987

십이십면체 그래프

십이십면체 그래프
5-배 대칭 슐레겔 도표
꼭짓점	60
가장자리	150
자기형태학	60
특성.	해밀턴 연산자, 정규 연산자
그래프 및 매개변수 표

그래프 이론에서, 스누브 십이면체 그래프는 아르키메데스 다면체 중 하나인 스누브 십이면체의 꼭짓점과 모서리의 그래프입니다.이것은 60개의 꼭짓점과 150개의 모서리를 가지고 있으며 아르키메데스 ^[2]그래프입니다.

참고 항목

• 평면 다각형에서 다면체로의 변환 애니메이션
• ccw 및 cw 회전 스누브 십이면체

레퍼런스

• Jayatilake, Udaya (March 2005). "Calculations on face and vertex regular polyhedra". Mathematical Gazette. 89 (514): 76–81. doi:10.1017/S0025557200176818. S2CID 125675814.
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (섹션 3-9)
• Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2.

외부 링크

• Eric W. Weisstein, Snub dodecahedron (Archimedean solid) at MathWorld.
  • Weisstein, Eric W. "Snub dodecahedral graph". MathWorld.
• Klitzing, Richard. "3D convex uniform polyhedra s3s5s - snid".
• 대화형 3D 보기를 사용하는 Snub Dodecaidel의 편집 가능한 인쇄 가능한 네트
• 고른 다면체
• 가상 현실 다면체 다면체 백과사전
• 마크 S. 아담스와 멘노 T. 코스터스.스너브 십이면체에 대한 부피해