Search

슈바르츠 삼각형

Schwarz triangle

기하학에서 헤르만 슈바르츠의 이름을 딴 슈바르츠 삼각형은 구(구형 타일링)의 가장자리 반사를 통해 겹칠 수 있는 구(구형 타일링)를 타일하는 데 사용할 수 있는 구면 삼각형이다. 그들은 (슈워즈 1873년)에 분류되었다.

이것들은 구체, 유클리드 평면 또는 쌍곡면의 테셀레이션으로 더 일반적으로 정의할 수 있다. 구체의 각 슈바르츠 삼각형은 유한 집단을 정의하는 반면 유클리드나 쌍곡면에서는 무한 집단을 정의한다.

슈바르츠 삼각형은 각각 정점에서 각도를 나타내는 세 개의 합리적인 숫자(p q r)로 표현된다. n/d 값은 정점 각도가 반원의 d/n임을 의미한다. "2"는 직각 삼각형을 의미한다. 이들이 정수일 때는 삼각형을 뫼비우스 삼각형이라고 하며, 겹치지 않는 타일링에 해당하며, 대칭 그룹을 삼각형 집단이라고 한다. 구체에는 뫼비우스 삼각형 세 개와 1개 매개변수 한 개 집단이 있다. 평면에는 뫼비우스 삼각형이 세 개 있는 반면 쌍곡선 공간에는 뫼비우스 삼각형 세 개 집단이 있고, 예외적인 물체는 없다.

솔루션 공간

정점 $각도$ 가 // $p$ , //q, //r인 기본 영역 삼각형(p q r)은 다음 정수의 왕복선 합계에 따라 다른 공간에 존재할 수 있다.

{\begin{aligned}{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&>1{\text{ : Sphere}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&=1{\text{ : Euclidean plane}}\\[8pt]{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}&<1{\text{ : Hyperbolic plane}}\end{aligned}}

이것은 유클리드 공간에서는 삼각형의 내부 각도가 $π$ 에 이르는 반면 $구체$ 에서는 than보다 큰 각도에, 쌍곡선 공간에서는 sum보다 작은 각도에 해당한다는 것을 단순히 말해주는 방법이다.

그래픽 표현

슈바르츠 삼각형은 삼각형 그래프로 그래픽으로 표현된다. 각 노드는 슈바르츠 삼각형의 가장자리(거울)를 나타낸다. 각 가장자리는 π/vertex 각도로 반사 순서에 해당하는 합리적인 값으로 라벨을 표시한다.

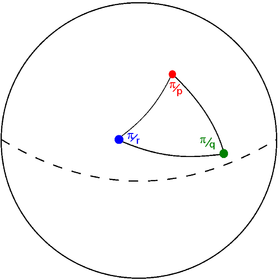구체의 슈바르츠 삼각형(pqr)	슈바르츠 삼각형 그래프

순서-2 에지는 이 다이어그램에서 무시할 수 있는 수직 미러를 나타낸다. Coxeter-Dynkin 도표는 순서 2 가장자리가 숨겨져 있는 이 삼각형 그래프를 나타낸다.

Coxeter 그룹은 (p q r) 주기 그래프의 경우, 그리고 (p q 2) = (오른쪽 삼각형)의 경우 [p,q], (p 2) = [p]×[]]]처럼 더 간단한 표기법에 사용할 수 있다.

슈바르츠 삼각형 목록

뫼비우스의 구 삼각형

(2 2 2) 또는 [2,2]	(3 2 2) 또는 [3,2]	...
(3 3 2) 또는 [3,3]	(4 3 2) 또는 [4,3]	(5 3 2) 또는 [5,3]

뫼비우스 삼각형이라고도 불리는 정수를 가진 슈바르츠 삼각형에는 1개의 파라미터 계열과 3개의 예외적인 경우를 포함한다.

[p,2] 또는 (p 2 2) – 치골 대칭,
[3,3] 또는 (3 3 2) – 사면 대칭,
[4,3] 또는 (4 3 2) – 팔면 대칭,
[5,3] 또는 (5 3 2) – 이코사헤드랄 대칭,

밀도별 구에 대한 슈바르츠 삼각형

밀도별로 그룹화된 슈바르츠 삼각형(p q r):

밀도	디헤드랄	사면체	팔면체	이코사헤드랄
d	(2 2 n/d)
1		(2 3 3)	(2 3 4)	(2 3 5)
2		(3/2 3 3)	(3/2 4 4)	(3/2 5 5), (5/2 3 3)
3		(2 3/2 3)		(2 5/2 5)
4			(3 4/3 4)	(3 5/3 5)
5		(2 3/2 3/2)	(2 3/2 4)
6		(3/2 3/2 3/2)		(5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7			(2 3 4/3)	(2 3 5/2)
8				(3/2 5/2 5)
9				(2 5/3 5)
10				(3 5/3 5/2), (3 5/4 5)
11			(2 3/2 4/3)	(2 3/2 5)
13				(2 3 5/3)
14			(3/2 4/3 4/3)	(3/2 5/2 5/2), (3 3 5/4)
16				(3 5/4 5/2)
17				(2 3/2 5/2)
18				(3/2 3 5/3), (5/3 5/3 5/2)
19				(2 3 5/4)
21				(2 5/4 5/2)
22				(3/2 3/2 5/2)
23				(2 3/2 5/3)
26				(3/2 5/3 5/3)
27				(2 5/4 5/3)
29				(2 3/2 5/4)
32				(3/2 5/4 5/3)
34				(3/2 3/2 5/4)
38				(3/2 5/4 5/4)
42				(5/4 5/4 5/4)

유클리드 평면의 삼각형

(3 3 3)	(4 4 2)	(6 3 2)

밀도 1:

(3 3 3) – 60-60-60(등각),
(4 4 2) – 45-45-90(이소셀 오른쪽),
(6 3 2) – 30-60-90,

밀도 2:

(6 6 3/2) - 120-30-30-30 삼각형

밀도 ∞:

(4 4/3 ∞)
(3 3/2 ∞)
(6 6/5 ∞)

쌍곡면 삼각형

(7 3 2)	(8 3 2)	(5 4 2)
(4 3 3)	(4 4 3)	(∞ ∞ ∞)
(p q r) 삼각형의 기본 도메인

밀도 1:

(2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
(2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
(2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
(2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
(3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
(3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
(3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
(3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
...
(∞ ∞ ∞)

밀도 2:

(3/2 7 7), (3/2 8 8), (3/2 9 9) ... (3/2 ∞ ∞)
(5/2 4 4), (5/2 5 5), (5/2 6 6) ... (5/2 ∞ ∞)
(7/2 3 3), (7/2 4 4), (7/2 5 5) ... (7/2 ∞ ∞)
(9/2 3 3), (9/2 4 4), (9/2 5 5) ... (9/2 ∞ ∞)
...

밀도 3:

(2 7/2 7), (2 9/2 9), (2 11/2 11) ...

밀도 4:

(7/3 3 7), (8/3 3 8), (3 10/3 10), (3 11/3 11) ...

밀도 6:

(7/4 7 7), (9/4 9 9), (11/4 11 11) ...
(7/2 7/2 7/2), (9/2 9/2 9/2), ...

밀도 10:

(3 7/2 7)

(2 3 7) 슈바르츠 삼각형은 가장 작은 쌍곡선 슈바르츠 삼각형이며, 이와 같이 특히 관심이 많다. 그것의 삼각형 그룹(또는 보다 정확하게는 방향 유지 등소계 지수 2 von Dyck 그룹)은 (2,3,7) 삼각형 그룹이며, 이는 모든 허위츠 그룹 - 리만 표면의 등소계 최대 그룹이다. 모든 후르비츠 그룹은 (2,3,7) 삼각형 그룹의 인용구이며, 모든 후르비츠 표면은 (2,3,7) 슈바르츠 삼각형에 의해 타일링된다. 가장 작은 후르비츠 그룹은 순서가 168인 단순 그룹이며, 두 번째로 작은 비아벨리안 단순 그룹으로서 PSL(2,7)에 이형이며, 관련 후르비츠 표면(3속)은 클라인 쿼티크이다.

(2 3 8) 삼각형은 속 2의 매우 대칭(그러나 허위츠는 아님) 표면인 볼자 표면과 타일을 이룬다.

위에 열거한 비정수자 각도가 1개 있는 삼각형은 앤서니 W. 크냅이 먼저 분류했다.^[1] 복수의 비정수자 각도가 있는 삼각형 목록이 에 제시되어 있다.^[2]

참고 항목

참조

^ A. W. Knapp, 이중 생성 Fuchsian 그룹, Michigan Mathical Journal 15(1968), No. 3, 289–304
^ 클림멘코와 사쿠마, 방향반복 요소를 포함하는 이솜(H 2 )의 2세대 이산형 부분군, 기하학적 디디카타 1998년 10월, 제72권, 제3권, 제247-282권

Coxeter, H.S.M. (1973), Regular Polytopes (Third ed.), Dover Publications, ISBN 0-486-61480-8, 표 3: 슈바르츠의 삼각형
Magnus, Wilhelm (1974), Noneuclidean Tesselations and Their Groups, Academic Press, ISBN 0080873774
Schwarz, H.A.(1873년),"Ueber diejenigen Fällewelchen 다이 Gaussichen hypergeometrische Reihe에 eine algebraische 기능 ihresvierten Elementes darstellt", 저널(다는 것 Coxeter 참조 이 벳술 Theorie하는 선전으로 다이 순수 운트angewandte Mathematik, 1873년(75):292–335, doi:10.1515/crll.1873.75.292, ISSN 0075-4102, S2CID 121698536 für.Rgeometrischen Reihe"은 짧은 타이틀은 잡지 페이지 표제의).

Wenninger, Magnus J. (1979), "An introduction to the notion of polyhedral density", Spherical models, CUP Archive, pp. 132–134, ISBN 978-0-521-22279-2

외부 링크

Weisstein, Eric W. "Schwarz triangle". MathWorld.
Klitzing, Richard. "3D The general Schwarz triangle (p q r) and the generalized incidence matrices of the corresponding polyhedra".

테셀레이션

주기적
피타고라스 롬빌 슈바르츠 삼각형 직사각형 도미노 균일 타일링 및 벌집형 컬러링 볼록스 키스롬빌 벽지 그룹 와이토프

Marble floor mosaic Basilica of St Mark Vencice.jpg

아페리오딕
암만-베인커 프로토타일 무주기 집합 리스트 아인슈타인 문제 소콜라-테일러 길버트 펜로즈 오각형 바람개비 콰콰이버설 Rep-tile 및 Self-tiling 스핑크스 트루체트

기타
음이소헤드랄과 이소헤드랄 건축 및 강직 서클 리미트 III 컴퓨터 그래픽스 벌집 동위원소 리스트 포장 문제 도미노 왕 헤슈의 스쿼링 프로토타일 콘웨이 기준 기리히 평면의 정기분할 때 정규 격자 대체 보로노이 주 보더버그

정점 유형별

구면	2ⁿ 3³.n V3³.n 4².n V4².n
정규	2^∞ 3⁶ 4⁴ 6³
세미- 정칙의	3².4.3.4 V3².4.3.4 3³.4² 3³.∞ 3⁴.6 V3⁴.6 3.4.6.4 (3.6)² 3.12² 4².∞ 4.6.12 4.8²
하이퍼- 볼록한	3².4.3.5 3².4.3.6 3².4.3.7 3².4.3.8 3².4.3.∞ 3².5.3.5 3².5.3.6 3².6.3.6 3².6.3.8 3².7.3.7 3².8.3.8 3³.4.3.4 3².∞.3.∞ 3⁴.7 3⁴.8 3⁴.∞ 3⁵.4 3⁷ 3⁸ 3^∞ (3.4)³ (3.4)⁴ 3.4.6².4 3.4.7.4 3.4.8.4 3.4.∞.4 3.6.4.6 (3.7)² (3.8)² 3.14² 3.16² (3.∞)² 3.∞² 4².5.4 4².6.4 4².7.4 4².8.4 4².∞.4 4⁵ 4⁶ 4⁷ 4⁸ 4^∞ (4.5)² (4.6)² 4.6.12 4.6.14 V4.6.14 4.6.16 V4.6.16 4.6.∞ (4.7)² (4.8)² 4.8.10 V4.8.10 4.8.12 4.8.14 4.8.16 4.8.∞ 4.10² 4.10.12 4.12² 4.12.16 4.14² 4.16² 4.∞² (4.∞)² 5⁴ 5⁵ 5⁶ 5^∞ 5.4.6.4 (5.6)² 5.8² 5.10² 5.12² (5.∞)² 6⁴ 6⁵ 6⁶ 6⁸ 6.4.8.4 (6.8)² 6.8² 6.10² 6.12² 6.16² 7³ 7⁴ 7⁷ 7.6² 7.8² 7.14² 8³ 8⁴ 8⁶ 8⁸ 8¹² 8.6² 8.16² ∞³ ∞⁴ ∞⁵ ∞^∞ ∞.6² ∞.8²

Schwarz_triangle / CC-BY-SA / 이용약관 (Terms)