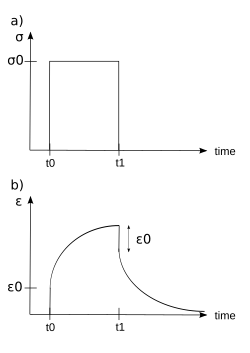
점탄성

다음에 대한 시리즈 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ 픽의 확산 법칙
법 컨버지 미사 모멘텀 에너지 불평등 클라우시우스-듀헴 (엔트로피)
고체 역학 변형 탄력성 일직선의 가소성 후크의 법칙 스트레스 유한변형 무한 변형률 호환성. 벤딩 접촉 역학 마찰의 물질적 고장 이론 파단 역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점도 (뉴턴어 · 비뉴턴어) 부력 · 믹싱 · 압력 액체 접착 모세관 작용 크로마토그래피 응집(화학) 표면장력 가스 대기 보일의 법칙 찰스의 법칙 복합가스법 픽의 법칙 게이 루삭의 법칙 그레이엄의 법칙 플라즈마
리히로지 점탄성 레호메트리 레히미터 스마트 유체 전기오류 자기 지질학 페로플루이드
과학자들 베르누이 보일 카우치 찰스 오일러 픽 게이 루삭 그레이엄 훅 뉴턴 나비에르 노울 파스칼 스톡스 트뤼셀
v t

재료 과학과 연속체 역학에서 점성성은 변형을 겪을 때 점성과 탄성 특성을 모두 나타내는 재료의 특성이다. 물과 같은 점성 물질은 전단 흐름에 저항하며 응력이 가해지는 시간에 따라 선형적으로 변형된다. 탄성 재료는 늘어나면 무리를 하고, 스트레스가 제거되면 즉시 원상태로 돌아간다.

점탄성 물질은 이러한 특성 두 가지 요소를 모두 가지고 있으며, 따라서 시간에 따른 변형을 나타낸다. 탄성은 보통 순서가 정해진 고체에서 결정학적 평면을 따라 늘어나는 결합의 결과인 반면에 점성은 무정형 물질 내부의 원자나 분자의 확산의 결과물이다.^[1]

배경

19세기에 맥스웰, 볼츠만, 켈빈과 같은 물리학자들은 유리, 금속, 고무의 크리프와 회수를 연구하고 실험했다. 점탄성은 합성 중합체가 다양한 용도에 설계되고 사용되었을 때 20세기 후반에 추가적으로 검토되었다.^[2] 점성성 계산은 점성 변수 η에 크게 의존한다. η의 역행은 유동성 φ이라고도 한다. 둘 중 하나의 값은 온도의 함수 또는 주어진 값(즉, 대시팟의 경우)으로 도출될 수 있다.^[1]

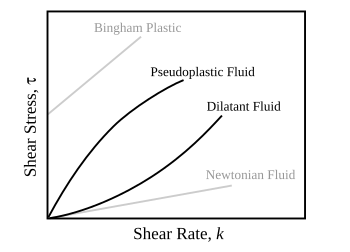
재료 내부의 변형률 대 응력의 변화에 따라 점도는 선형, 비선형 또는 플라스틱 반응을 갖는 것으로 분류할 수 있다. 물질이 선형 반응을 보일 때 뉴턴 물질로 분류된다. 이 경우 스트레스는 변형률에 선형 비례한다. 이 물질이 변형률에 비선형 반응을 보일 경우 비뉴턴 액으로 분류된다. 전단/변형률이 일정하게 유지되면서 점도가 떨어지는 흥미로운 사례도 있다. 이러한 유형의 행동을 보이는 물질을 이산화질소라고 한다. 또한 응력이 이 변형률과 무관할 때 재료는 소성변형을 보인다.^[1] 많은 점탄성 물질은 고분자 탄력의 열역학 이론에 의해 설명되는 고무와 같은 행동을 나타낸다.

점탄성 물질의 일부 예로는 비정형 중합체, 세미스트리탈린 중합체, 생물폴리머, 매우 높은 온도에서의 금속, 비투멘 재료 등이 있다. 균열은 균열이 탄성 한계를 벗어나 빠르게 가해졌을 때 발생한다. 인대와 힘줄은 점탄성이기 때문에, 인대에 대한 잠재적 손상의 정도는 길이 변화율뿐만 아니라 가해지는 힘에도 달려 있다.^{[citation needed]}

점탄성 물질은 다음과 같은 특성을 갖는다.

• 이력(hysteresis)은 스트레스-증가 곡선에서 나타난다.
• 스트레스 이완 발생: 스텝 상수 스트레인은 스트레스 감소의 원인
• 크리프가 발생함: 스텝 상수 스트레스는 스트레인을 증가시킨다.
• 그 강성은 변형률${\$ 또는$$ 응력률 ${\${\dot${\$dot{\$ma}}}$에 따라 달라진다.

탄성 대 점탄성 거동

순수하게 탄성물질과 달리 점성물질은 탄성부재와 점성부재를 가지고 있다. 점성 물질의 점성은 물질에 시간에 따른 변형률 의존성을 준다. 순탄성 물질은 하중을 가한 후 제거할 때 에너지(열)를 방출하지 않는다. 그러나 점탄성 물질은 하중을 가한 다음 제거하면 에너지를 분산시킨다. 이력(hysteresis)은 응력-스트레인 곡선에서 관찰되며, 루프 면적이 하중 주기 동안 손실된 에너지와 동일하다. 점성은 열로 작동되는 플라스틱 변형에 대한 저항성이기 때문에 점성 물질은 부하 사이클을 통해 에너지를 잃게 된다. 소성변형은 에너지 손실을 초래하는데, 이것은 하중 주기에 대한 순전히 탄성 재료의 반응과는 다른 특성이다.^[1]

구체적으로는 점탄성이 분자 재배열이다. 폴리머와 같은 점탄성 물질에 응력이 가해지면 긴 폴리머 체인의 일부가 위치를 바꾼다. 이런 움직임이나 재배치를 크리프라고 한다. 중합체는 체인의 이 부분들이 스트레스에 동반하기 위해 재배열하고 있을 때에도 견고한 재료로 남아 있으며, 이 과정에서 재료에 등응력이 생기게 된다. 허리 응력이 가해진 스트레스와 크기가 같을 때, 물질은 더 이상 구불구불하지 않는다. 원래의 스트레스를 제거하면 축적된 허리 스트레스로 인해 폴리머가 원래의 형태로 되돌아오게 된다. 재료는 접두사 visco를 주고 재료는 완전히 회복되어 접미사 -탄력성을 부여한다.^[2]

종류들

선형 점탄성은 함수가 크리프 반응과 부하에서 모두 분리될 수 있는 경우를 말한다. 모든 선형 점탄성 모델은 응력과 변형을 연결하는 볼테라 방정식으로 표현될 수 있다.

또는

어디에

• t는 시간이다.
• ${\displaystyle \sigma }$( ${\displaystyle t}$) ${\displaystyle \sigma (t)}$이(가) 스트레스임
• ${\displaystyle \epsilon }$( ${\displaystyle t}$) ${\displaystyle \varepsilon (t)}$이(가) 변형률임
• ${\displaystyle E_{}}$$$ ${\displaystyle {\text{inst,creep}}_{}}$ ${\$${\$$text{$$inst$$,creep}}$ 및$$ $E{\displaystyle {}_{}}$ $,$은(는) 크리프와 이완을 위한 즉각적인 탄성 모듈이다$.$
• K(t)는 크리프 기능이다.
• F(t)는 이완 기능이다.

선형 점탄성은 보통 작은 변형에만 적용된다.

비선형 점탄성은 함수를 분리할 수 없을 때를 말한다. 일반적으로 변형이 크거나 변형에 따라 재료의 특성이 바뀔 때 발생한다. 비선형 점탄성은 또한 점탄성 유체에서 정상 응력, 전단 박리, 확장성 두꺼워짐과 같은 관찰된 현상을 해명한다.^[3]

비탄성 물질은 비탄성 물질의 특별한 경우로서, 비탄성 물질은 하중 제거 시 원래의 상태로 완전히 회복될 것이다.

탄성, 점성, 점성 및 형태의 점성 행동을 구별할 때 다음과 같은 경우 데보라 번호(De)로 알려진 관찰되는 물질의 이완 시간에 상대적인 측정의 시간 척도를 참조하는 것이 도움이 된다.^[4]

어디에

• $【\displaystyle \lambda 】$ ${\displaystyle \mathrm{재료}}$의 이완 시간$$
• ${\displaystyle t}$ $[\displaystyle t}$은(는) 시간임

동적 계수

점탄성은 동적 기계적 분석을 사용하여 작은 진동 응력을 적용하고 결과 변형을 측정하여 연구한다.

• 순탄성 물질은 단계별로 응력과 긴장감을 갖고 있어 다른 물질에 의해 발생하는 한 물질에 대한 반응이 즉각적이다.
• 순전히 점성 물질에서 스트레인은 스트레스를 90도 상으로 지연시킨다.
• 점탄성 물질은 이 두 종류의 물질 가운데 어딘가에서 행동을 보이며, 변형률에서 다소 지연을 보인다.

복합 동적 계수 G는 진동 응력과 변형률 사이의 관계를 나타내기 위해 사용될 수 있다.

${\displaystyle \mathrm{여기}}$서 $i{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$=${\displaystyle }$- 1 ${\displaystyle$ i$^{2}=-1$ $G{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$은(는) 스토리지 계량이고 $G{\displaystyle {}^{}}$ ${\displaystyle {″}^{}}$ ${\$ G$'}$은(는) 손실 계량이다.

여기서 $\sigma {\displaystyle {}_{}}$ ${\$과 ${\displaystyle {\epsilon \mathrm{}}_{}}$ 0 ${\$은 각각 스트레스와 스트레인의 진폭이며$$, $\Delta {\displaystyle }$ ${\displaystyle \delta}$은 그들 사이의 위상 변화다.

선형 점탄성의 구성 모델

무정형 중합체, 세미스트리탈린 중합체, 생물폴리머 그리고 심지어 살아있는 조직과 세포와 세포와 같은 점탄성 물질들은 그들의 시간적 의존성뿐만 아니라 스트레스, 변형력, 힘 그리고 변위 상호작용들을 결정하기 위해 모델링될 수 있다.^[5] 맥스웰 모델, 켈빈-Voigt 모델, 표준 선형 솔리드 모델 및 버거 모델을 포함하는 이 모델들은 서로 다른 하중 조건에서 물질의 반응을 예측하는 데 사용된다.

점탄성 거동은 각각 스프링과 대시보트의 선형 조합으로 모델링된 탄성 및 점성 성분을 가지고 있다. 각 모델은 이러한 요소의 배열이 다르며, 이러한 모든 점탄성 모델은 전기 회로로 동등하게 모델링될 수 있다.

등가 전기회로에서 응력은 전류로, 변형률은 전압으로 나타낸다. 스프링의 탄성 계수는 회로의 캐패시턴스(에너지를 저장함)와 유사하며 회로의 저항에 대한 대시팟의 점성(에너지를 소멸함)과 유사하다.

앞에서 언급한 바와 같이 탄성 구성 요소는 다음과 같은 공식으로 볼 때 탄성 상수 E의 스프링으로 모델링할 수 있다.

여기서 σ은 스트레스, E는 물질의 탄성계수, ε은 주어진 스트레스 하에서 발생하는 스트레스로 후크의 법칙과 유사하다.

비스코스 구성 요소는 다음과 같이 응력-변형률 관계를 제공할 수 있도록 대시팟으로 모델링할 수 있다.

여기서 σ은 응력, η은 물질의 점성, dε/dt는 스트레인의 시간 파생이다.

스트레스와 스트레인의 관계는 특정한 스트레스나 스트레인 비율에 대해 단순화할 수 있다. 높은 스트레스 또는 변형률/단기 기간의 경우 스트레스-스트레인 관계의 시간 파생 요소들이 지배적이다. 이러한 조건에서는 변형 없이 높은 하중을 지탱할 수 있는 강체 로드로 대략 추정할 수 있다. 따라서 대시보드는 "단락 회로"^[6][7]로 간주할 수 있다.

반대로 저응력 상태/장시간의 경우, 시간 파생 요소들은 무시할 수 있고 대쉬팟은 시스템에서 효과적으로 제거될 수 있다 – 즉 "개방" 회로.^[7] 그 결과, 대시보드에 병렬로 연결된 스프링만이 시스템의 총 변형률에 기여하게 된다.^[6]

맥스웰 모델

Maxwell 모델은 다이어그램에 나타난 바와 같이 순전히 점성 댐퍼와 직렬로 연결된 순탄성 스프링으로 나타낼 수 있다. 모델은 다음과 같은 방정식으로 나타낼 수 있다.

이 모델에서 재료가 일정한 스트레스에 처하게 되면 스트레스는 점차 완화된다. 물질이 일정한 스트레스를 받으면 변형률에는 두 가지 성분이 있다. 첫째, 탄력성 성분이 즉각적으로 발생하여 스프링에 해당하며, 스트레스가 풀리면 즉시 이완된다. 두 번째는 응력이 가해지는 한 시간이 지날수록 커지는 점성 성분이다. 맥스웰 모델은 스트레스는 시간에 따라 기하급수적으로 감소하며, 이는 대부분의 폴리머에 대해 정확하다고 예측한다. 이 모델의 한 가지 제한은 크리프를 정확하게 예측하지 못한다는 것이다. 크리프 또는 상수압 조건의 맥스웰 모델은 스트레인이 시간에 따라 선형적으로 증가한다고 가정한다. 그러나 대부분의 폴리머는 시간이 지날수록 변형률이 감소하고 있음을 보여준다.^[2]

이 모델은 용해 온도 근처의 열가소성 중합체, (노화 불순) 신선한 콘크리트, 그리고 용해점에 가까운 온도에서 수많은 금속 등 부드러운 고형물에 적용할 수 있다.

켈빈-비그트 모형

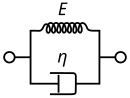
Voigt 모델로도 알려진 켈빈-Voigt 모델은 그림과 같이 뉴턴 댐퍼와 후크 탄성 스프링이 병렬로 연결되어 있다. 폴리머의 크리프 행동을 설명하기 위해 사용된다.

구성 관계는 선형 1차 미분 방정식으로 표현된다.

이 모델은 가역성, 점탄성 변형을 겪고 있는 고체를 나타낸다. 일정한 응력을 가하면 물질이 감소 속도로 변형되어 점증적으로 정상 상태 변형에 접근한다. 스트레스가 풀리면 그 물질은 점차 변형되지 않은 상태로 이완된다. 일정한 스트레스(creep)에서 모델은 시간이 무한대로 지속됨에 따라 σ/E 경향이 있는 스트레인을 예측하기 때문에 상당히 현실적이다. 맥스웰 모델과 유사하게 켈빈-비그트 모델도 한계가 있다. 이 모델은 재료의 크리프 모델과 함께 매우 훌륭하지만, 이완과 관련하여 모델은 훨씬 덜 정확하다.^[8]

이 모델은 하중이 너무 높지 않을 때 유기 중합체, 고무, 목재 등에 적용할 수 있다.

표준 선형 솔리드 모델

제너 모델이라고도 알려진 표준 선형 고체 모델은 두 개의 스프링과 대쉬팟으로 구성되어 있다. 점탄성 소재의 크리프와 스트레스 완화 동작을 모두 제대로 설명한 가장 단순한 모델이다. 이 모델의 경우, 지배적 구성 관계는 다음과 같다.

맥스웰 표현	켈빈 표현
${\displaystyle \sigma +{\frac {\eta }{E_{2}}:}{\dot{\sigma }}{\sigma }}}}}{\frac {1}{1}+E_{2}}}{E_}}{\dot {\varepsilon}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	${\displaystyle \sigma +{\frac {\eta }{E_{1}+E_{2}}}{{\dot{\sigma }}}={\frac {E_{1}E_{2}}:{E_{1}+E_{2}}}}\varepsilon +{\frac {E_{1}\eta }{E_{1}+E_{2}}}}{\dot {\barepsilon }}$

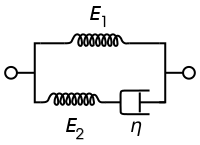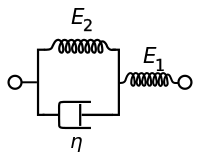일정한 응력 하에서 모델링된 재료는 즉각적으로 변형되며, 이는 스트레인의 순간 탄성 부분이다. 그 후에 그것은 계속 변형되고 점증적으로 균주의 지체 탄성 부분인 정상 상태 변종에 접근할 것이다. 표준 선형 솔리드 모델은 재료 반응을 예측하는 데 있어 맥스웰 및 켈빈-비그트 모델보다 더 정확하지만, 수학적으로 특정 하중 조건에서 변형률에 대한 부정확한 결과를 반환한다.

버거 모델

버거 모델은 병렬로 두 개의 맥스웰 구성 요소 또는 켈빈-Voigt 구성 요소, 스프링 및 대쉬팟으로 구성된다. 이 모델의 경우, 지배적 구성 관계는 다음과 같다.

맥스웰 표현	켈빈 표현
${\displaystyle \sigma +\left({\frac {\eta _{1}}{E_{1}}}+{\frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\left(\eta _{1}+\eta _{2}\right){\dot {\varepsilon }}+{\frac {\eta _{1}\eta _{2}\left(E_{1}+E_{2}\right)}{E_{1}E_{2}}:{\ddot{\barepsilon }}$	${\displaystyle \sigma +\left({\frac {\eta _{1}}{E_{1}}}+{\frac {\eta _{2}}{E_{1}}}+{\frac {\eta _{2}}{E_{2}}}\right){\dot {\sigma }}+{\frac {\eta _{1}\eta _{2}}{E_{1}E_{2}}}{\ddot {\sigma }}=\eta _{2}{\dot {\varepsilon }}+{\frac {\eta _{1}\eta _{2}}{E_{1}}}{\ddot {\varepsilon }}}$

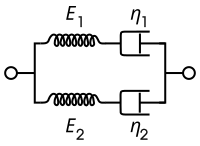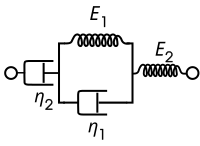이 모델은 비스코스 흐름을 표준 선형 고체 모델에 통합하여 고정 하중 조건에서 스트레인에 대해 선형적으로 증가하는 무증상 증세를 제공한다.

일반화 맥스웰 모델

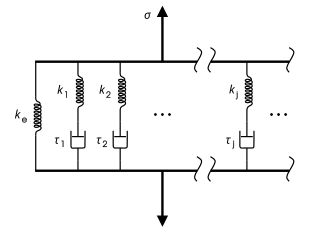
Wiechert 모델로도 알려져 있는 Generalized Maxwell 모델은 점탄성을 위한 선형 모델의 가장 일반적인 형태다. 이완이 한 번에 일어나는 것이 아니라 시간의 분포에서 일어나는 것을 고려한다. 길이가 다른 분자 세그먼트와 짧은 분자 세그먼트가 긴 분자보다 적게 기여하기 때문에 시간 분포가 다양하다. Wiechert 모델은 분포를 정확하게 나타내기 위해 필요한 만큼의 스프링-대시팟 맥스웰 요소를 가지고 있어 이를 보여준다. 오른쪽 그림은 일반화된 위쳇 모델을 보여준다.^[9] 용도: 절대 용해 온도의 4분의 1 미만의 온도에서 금속 및 합금(K로 표시됨)

비선형 점탄성을 위한 구성 모델

비선형 점탄성 구성 방정식은 정상 응력의 차이, 전단 박리 및 확장적 두께화와 같은 유체의 현상을 정량적으로 설명하기 위해 필요하다.^[10] 필연적으로 재료가 경험하는 이력은 시간 의존적인 행동을 설명하기 위해 필요하며, 일반적으로 이력 커널 K로서 모델에 포함된다.^[11]

2차 오일

2차 유체는 일반적으로 가장 단순한 비선형 점탄성 모델로 간주되며, 일반적으로 뉴턴 유체와 기타 복잡한 비선형 점탄성 유체 사이의 높은 변형 진폭과 데보라 수에서 발생하는 재료 거동의 좁은 영역에서 발생한다.^[12] 2차 유체 구성 방정식은 다음과 같다.

여기서:

• ${\displaystyle \mathbf{I}}$ ${\$은(는) ID 텐서입니다.
• ${\displaystyle \mathbf{D}}$ ${\$은(는) 변형 텐서임
• ${\displaystyle {\eta }_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {\psi \mathrm{}}_{}}$ 2 ${\${1$},\filences _{2$}} 각각 점도와 1차 및 2차 정상 응력 계수를 나타낸다$$.
• ${\displaystyle {\mathbf{D}.}^{}}$ ${\$은 변형$$ 텐서의 상부결합 파생물을 의미한다.

and ${\displaystyle {\dot {\mathbf {D}}}\equiv {\frac {\partial }{\partial t}}{\mathbf {D}}+{\mathbf {v}}\bullet \bigtriangledown {\mathbf {D}}}$is the material time derivative of the deformation tensor.^[13]

상부 콘벡트 맥스웰

상부 컨버전스 맥스웰 모델은 비선형 시간 거동을 점탄성 맥스웰 모델에 통합하며,^[14] 다음과 같이 제공된다.

여기서:

• ${\displaystyle \tau }$ ${\$은(는) 스트레스 텐서 표시$$

올드로이드-B 모델

올드로이드-B 모델은 어퍼볼록티드 맥스웰 모델을 확장한 것으로 탄성 비드와 스프링 아령으로 채워진 용제로 해석된다. 이 모델은 제작자 제임스 G의 이름을 따서 명명되었다. 올드로이드^{[15] [16] [17]}

모델은 다음과 같이 쓸 수 있다.

여기서:

• ${\displaystyle \mathbf{T}}$ ${\$은$($는) 스트레스 텐서;
• ${\displaystyle {\lambda }_{}}$ ${\$}는$$ 휴식 시간이다.
• ${\displaystyle {\lambda }_{}}$ ${\$}}은$$ 지연시간 = ${\displaystyle \frac{{\eta }_{}}{}}$ ${\displaystyle \frac{{s\mathrm{}}_{}}{}}$ 0 ${\displaystyle \frac{{}_{}}{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$eta $_{s}{\eta _{0}}\\da _{1$
• ${\displaystyle \stackrel{}{\mathbf{T}}}$ ${\displaystyle \stackrel{\mathrm{}}{\nabla }}$ ${\$은(는$$) 스트레스 텐서의 상부 대류 시간 파생물이다.
  $${\displaystyle {\stackrel {\nabla }{\mathbf {T} }}={\frac {\partial }{\partial t}}\mathbf {T} +\mathbf {v} \cdot \nabla \mathbf {T} -((\nabla \mathbf {v} )^{T}\cdot \mathbf {T} +\mathbf {T} \cdot (\nabla \mathbf {v} ));}$$

  
• ${\displaystyle \mathbf{v}}$ ${\$이$($가) 유체 속도임.
• ${\displaystyle {\eta }_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$는 용매와 폴리머 성분으로 구성된 총 점도이며, ${\displaystyle {\eta \mathrm{}}_{}}$ 0${\displaystyle {}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle s_{}}$+ ${\displaystyle {\eta }_{}}$ p ${\$ ;
• ${\displaystyle \mathbf {D} }$ is the deformation rate tensor or rate of strain tensor, ${\displaystyle \mathbf {D} ={\frac {1}{2}}\left[{\boldsymbol {\nabla }}\mathbf {v} +({\boldsymbol {\nabla }}\mathbf {v} )^{T}\right]}$.

모델은 전단 흐름에서 점탄성 유체의 좋은 근사를 제공하지만, 아령이 무한히 늘어나는 확장 흐름에서 비물리적 특이성을 가진다. 그러나 이것은 이상화된 흐름으로 한정된다. 교차 슬롯 기하학의 경우 확장적 흐름은 이상적이지 않기 때문에, 비록 단수적이긴 하지만, 응력이 무한히 작은 지역에서 무한히 존재하지만, 응력은 통합 가능한 상태를 유지한다.^[17]

용제 점도가 0이면 Oldroyd-B는 상부 볼록 맥스웰 모델이 된다.

바그너 모델

바그너 모델은 번스타인-커슬리-자파스 모델의 단순화된 실용적인 형태로 간주될 수 있다. 이 모델은 독일의 연구자 만프레드 바그너에 의해 개발되었다.

등온 조건의 경우 모델은 다음과 같이 기록할 수 있다.

여기서:

• ${\displaystyle \sigma }$( ${\displaystyle t}$) ${\displaystyle \mathbf {\sigma }(t)}$은 시간 t의 함수로서 Cauchy 스트레스 텐서이다.
• p는 압력이다.
• ${\displaystyle \mathbf{I}}$ ${\$은$($는) 통합 텐서임
• M은 일반적으로 각 이완 모드에 대한 지수 항의 합으로 표현되는 메모리 기능이다.

, 각 이완 모드에 $대해{\displaystyle {}_{}}$ g ${\displaystyle i_{}}$ ${\$는 이완 계량이고 $\theta {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 이완$$ 시간이다.

• ${\displaystyle h}$( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$) ${\displaystyle h(I_{1},I_{2}})$는 핑거 텐서 B {\$displaystyle \mathbf {B}$의 첫 번째 및 두 번째 불변수에 따라 달라지는 변형률 댐핑 기능이다$.$

스트레인 댐핑 기능은 보통 다음과 같이 기록된다.

변형률 강화 함수의 값이 1과 같으면 변형이 작고, 0에 가까우면 변형이 크다.^[18][19]

프레니 시리즈

1차원 이완 시험에서 재료는 시험 기간 동안 일정하게 유지되는 급작스런 스트레스에 노출되며, 스트레스는 시간이 지남에 따라 측정된다. 초기 응력은 재료의 탄성 반응에 기인한다. 그 다음 재료의 점성 효과로 인해 시간이 지남에 따라 스트레스가 완화된다. 일반적으로 인장, 압축, 벌크 압축 또는 전단 변형률이 적용된다. 결과 응력 대 시간 데이터는 모형이라고 하는 여러 방정식으로 적합될 수 있다. 적용된 변형률의 종류에 따라 표기법만 변경된다: 인장압축 $이완$은 E ${\displaystyle$ E$\},$ 전단 $이완$은 G ${\displaystyle G$ 벌크는 $K{\displaystyle }$ ${\displaystyle K}$로 표시된다$.$ 전단 이완을 위한 Prony 시리즈는 다음과 같다.

여기서 $∞{\$는 재료가 완전히 이완된 후 장기 계수로, ${\displaystyle {\tau }_{}}$ i ${\$ $\$$tau_{i}$는 이완$$ 시간(도표에서$$ ${\displaystyle {\tau }_{}}$ i ${\$ \$tau_{i}$와 혼동하지 않음)이며, 값이 높을수록 스트레스가 이완되는 시간이 길어진다. 예측값과 데이터 값 사이의 오차를 최소화하기 위해 매개변수(${\displaystyle {}_{}}$ ${\displaystyle {\infty \mathrm{}}_{}}$ ,${\displaystyle {}_{}{G}_{}}$ , ${\displaystyle i_{}}$ i$${\$displaystyle G_{\infit },G_{i},\tau$ _${i$를 조정하는 최소화 알고리즘을 사용하여 데이터를 방정식으로 적합시킨다.^[20]

탄성계수가 장기계수와 관련이 있다는 점에 주목하는 대체형식을 얻는다.

그러므로

이 형태는 이완 데이터로부터 탄성 전단 계수 $G{\displaystyle {}_{}}$ ${\$을 얻을$$ 때, 그리고/또는 컴퓨터 구현을 위해 Simulia(2010)와 같이 점성 속성과 별도로 탄성 특성을 지정하고자 할 때 편리하다.^[21]

크리프 실험은 대개 이완 실험보다 수행하기가 쉬우므로 대부분의 데이터는 (creep) 준수 대 시간으로 이용할 수 있다.^[22] 불행히도 프론 시리즈 계수 측면에서 (creep) 준수에 대해 알려진 폐쇄형 양식은 없다. 그래서 크리프 데이터를 가지고 있다면, 예를 들어 필요한 (완화)프론 계열의 계수를 구하기가 쉽지 않다.^[21] 이러한 계수를 얻기 위한 편법적인 방법은 다음과 같다. 먼저, 컴플라이언스 및 이완 양쪽에서 닫힌 폼 솔루션을 가진 모델에 크리프 데이터를 적합시킨다. 예를 들어, Barbero(2007년)의 Maxwell-Kelvin 모델(2007년)^[23][23] 또는 Barbero(2007년)의 Standard Solid Model(eq 7.20-7.21)을 사용한다. 크리프 모델의 매개변수가 알려지면 원래 데이터의 동일한 시간에 대한 결합 완화 모델로 이완 유사 데이터를 생성한다. 마지막으로 Prony 영상 시리즈로 유사 데이터를 적합시키십시오.

온도가 점탄성 거동에 미치는 영향

중합체의 2차 결합은 열운동으로 인해 끊임없이 끊어지고 개혁된다. 스트레스의 적용은 다른 것들보다 일부 순응을 선호하기 때문에 폴리머의 분자는 시간이 지남에 따라 점차 선호되는 순응으로 "흐름"될 것이다.^[24] 열운동은 폴리머의 변형에 기여하는 한 요인이기 때문에 온도가 증가하거나 감소함에 따라 점탄성 특성이 변한다. 대부분의 경우 시간에 따른 스트레스에 대한 가해지는 스트레스의 비율로 정의되는 크리프 계수는 온도가 증가함에 따라 감소한다. 일반적으로 말해서, 온도 증가는 일정한 스트레스에서 균등한 긴장을 전달하는데 필요한 시간의 로그 감소와 관련이 있다. 즉, 점탄성 물질을 낮은 온도에서 하는 것보다 높은 온도에서 같은 거리로 스트레칭하는 것은 덜 많은 작업이 필요하다.

폴리머의 점탄성 거동에 대한 온도의 보다 상세한 효과는 그림과 같이 나타낼 수 있다.

대표적인 중합체에는 주로 5개 지역(일부에서는 VI와 V를 합친 4개로 표시됨)이 포함되어 있다.^[25]

지역 I: 이 지역에서 폴리머의 유리 상태가 나타난다. 주어진 중합체의 이 부위의 온도는 분자 운동을 견디기엔 너무 낮다. 따라서 분자의 운동은 이 영역에서 동결된다. 이 지역은 기계적 특성이 단단하고 부서지기 쉽다.^[26]

지역 II: 폴리머는 이 지역의 유리 전환 온도를 통과한다. Tg를 넘어, 환경이 제공하는 열 에너지는 분자의 운동을 얼리기에 충분하다. 분자들은 이 지역에서 국소 운동을 할 수 있도록 허용되어 지역 I에 비해 강성이 급격히 감소한다.

지역 III: 고무 고원 지역. 이 지역에 존재하는 물질은 엔트로피에 의해 구동되는 장기 탄성이 존재할 것이다. 예를 들어, 고무 밴드는 이 지역의 초기 상태에서 정렬되지 않는다. 고무 밴드를 스트레칭할 때 구조물을 정렬하여 더 많은 순서를 정한다. 따라서 고무 밴드를 해제할 때 자연스럽게 더 높은 엔트로피 상태를 추구하게 되어 초기 상태로 되돌아간다. 이것이 바로 엔트로피(Entropy) 주도형 탄성 형상 회복이라고 부르는 것이다.

지역 IV: 고무 흐름 지역의 행동은 시간에 크게 의존한다. 이 지역의 폴리머는 재료 사용법을 신중하게 결정하기 위해 더 자세한 정보를 얻기 위해 시간 온도 중첩 위치를 사용해야 할 것이다. 예를 들어, 짧은 상호작용 시간 목적에 대처하기 위해 재료를 사용하는 경우, '하드' 재료로 나타낼 수 있다. 긴 상호작용 시간 목적으로 사용하는 동안, 그것은 '부드러운' 재료로 작용할 것이다.^[27]

지역 V: 이 지역에서는 점성 고분자가 쉽게 흐른다. 또 한 번 경직성이 현저하게 떨어졌다.

극도의 한랭한 온도는 점탄성 물질이 유리 단계로 변화하여 깨지기 쉽다. 예를 들어 압력에 민감한 접착제를 극저온(건식 얼음, 동결 스프레이 등)에 노출하면 태크가 없어져 디버딩이 발생한다.

점탄성 크리프

층계 상수 응력을 받으면 점탄성 물질은 시간에 따라 변형률이 증가한다. 이 현상은 점탄성 크리프로 알려져 있다.

시간 $t{\displaystyle {}_{}}$ ${\$에 점탄성 소재에 충분히 긴 시간 동안 유지되는 일정한 응력이 적재된다$.$ 물질은 응력에 반응하는 스트레스로 작용하는데, 만약 그것이 점탄성 액체라면 물질이 궁극적으로 실패할 때까지 증가한다. 반면에, 만약 그것이 점탄성 고체라면, 그것은 적용된 응력 대 재료의 궁극적인 저항성에 따라 고장날 수도 있고 고장나지 않을 수도 있다. 스트레스가 더 짧은 기간 동안 유지되면 재료는 ${\displaystyle {t\mathrm{}}_{}}$ $1{\displaystyle {}_{}}$ ${\$까지 초기 스트레인을 겪게 되며$,$ 그 후 스트레인은 즉시 감소(불연속성)한 후 > t ${\$ t > $t_t_{1}}}}$의 시간 경과 후 잔류 스트레인으로 점차 감소한다.

점탄성 크리프 데이터는 시간의 함수로 크리프 계수(특정 시간의 총 변형률로 나눈 일정한 적용 응력)를 플로팅하여 제시할 수 있다.^[28] 임계 스트레스 이하에서 점탄성 크리프 계수는 가해지는 스트레스와는 무관하다. 적용된 다양한 응력에 대한 변형률 대 시간 반응을 설명하는 곡선군은 적용된 응력이 물질의 임계 응력 값보다 낮은 경우 단일 점탄성 크리프 계수 대 시간 곡선으로 나타낼 수 있다.

장기 구조 설계를 고려할 때 점탄성 크리프는 중요하다. 하중 및 온도 조건의 경우 설계자는 구성 요소 수명에 가장 적합한 재료를 선택할 수 있다.

측정

전단 측량법

전단 온도계는 측정할 재료를 두 판 사이에 놓는 아이디어를 기반으로 하며, 이 중 하나 또는 둘 다 전단 방향으로 이동하여 재료의 응력과 균주를 유도한다. 시험은 일정한 변형률, 응력 또는 진동 방식(동적 기계적 분석의 한 형태)으로 수행될 수 있다.^[29] 전단 온도계는 일반적으로 재료가 두 플레이트 사이에서 새어 나와 재료/플레이트 인터페이스에서 미끄러질 수 있는 가장자리 효과에 의해 제한된다.

확장 레히메트리

신장계라고도 알려진 신장계수계는 전형적으로 단색적으로 점탄성 액체를 당김으로써 점탄성 특성을 측정한다.^[30] 이것은 일반적으로 모세관 힘을 사용하고 유체를 좁은 기하학적 구조로 구속하기 때문에, 이 기술은 희석된 폴리머 용액이나 일부 용해된 폴리머와 같이 점성이 상대적으로 낮은 유체로 제한된다.^[31] 또한 신장계 단부의 가장자리 효과와 모세관 내부와 외부 간의 압력 차이에 의해 확장력 계량계가 제한된다.^[32]

기타 방법

소재의 기계적 및 점탄성 반응을 시험하는 계측기가 많지만, 광대역 점탄성 분광법(BVS)과 공명성 초음파 분광법(RUS)은 주변 온도 위아래에서 사용할 수 있고 점탄성 시험에 더욱 특수하기 때문에 점탄성 행동을 시험하는 데 더 많이 사용된다. 이 두 계측기는 다양한 주파수 및 시간 범위에서 감쇠 메커니즘을 사용하며, 시간 온도 중첩에 영향을 미치지 않는다. 재료의 기계적 특성을 연구하기 위해 BVS와 RUS를 사용하는 것은 점탄성을 나타내는 재료가 어떻게 작동하는지 이해하는 데 중요하다.^[33]

참고 항목

참조

• 실비 및 앨버트(2001): 물리 화학 857번 존 와일리 & 선즈 주식회사
• Alan S. Wineman과 K. R. R. Rajagopal(2000): 폴리머의 기계적 반응: 소개
• 앨런과 토마스(1999년): 재료의 구조, 51.
• 크랜달 외 연구진(1999): 고형물 역학개론 348
• J. 르메트르와 J. L. 샤보체(1994) 고체 재료의 역학
• Yu. Dimitrienko(2011) 비선형 연속체 역학과 큰 비탄성 변형, 스프링거, 772p