각도 이등분자 정리

기하학에서, 각도 이등분 정리란 삼각형의 면이 반대 각도를 이등분하는 선으로 나뉘는 두 세그먼트의 상대적인 길이에 관계된다. 그것은 그들의 상대적인 길이를 삼각형의 다른 두 변의 상대적인 길이로 동일시한다.

정리

삼각형 ABC를 생각해보자. A 각도의 각도 이등분자가 B와 C 사이의 D 지점에서 BC 측을 교차하도록 한다. 각도 이등분자 정리에서는 세그먼트 CD의 길이에 대한 선분할 길이 BD의 비율이 옆면 AB의 길이와 옆면 AC의 길이에 대한 비율과 동일하다고 명시한다.

${\displaystyle {\frac {BD }{CD }}={\frac {AB }{ AC },}$

반대로, 삼각형 ABC의 측면 BC에 있는 점 D가 측면 AB와 AC와 동일한 비율로 BC를 나눈다면, AD는 각도 a A의 각도 이등분선이다.

일반화된 각도 이등분자 정리는 D가 BC 선에 놓여 있으면 그 다음이라고 기술하고 있다.

${\displaystyle {\frac {BD}{CD }}={\frac { AB \sin \angle DAB}{ AC \sin \angle DAC}}.}$

이는 AD가 ∠ BAC의 이등분자일 경우 이전 버전으로 줄어든다. D가 세그먼트 BC의 외부에 있는 경우, 방향 선 세그먼트와 방향 각도를 계산에 사용해야 한다.

앵글 이등분자 정리는 앵글 이등분자와 옆면 길이를 알 때 일반적으로 사용된다. 그것은 계산이나 증거에 사용될 수 있다.

정리의 즉각적인 결과는 이등변 삼각형의 정점 각도의 각도 이등분자가 반대쪽도 이등분한다는 것이다.

교정쇄

증명1길

위의 다이어그램에서 삼각형 ABD 및 ACD의 사인 법칙을 사용하십시오.

${\displaystyle {\frac {AB}{BD }}={\frac {\sin \angle ADB}{\sin \angle DAB}}}}}$

(1)

${\displaystyle {\frac {AC}{CD }}={\frac {\sin \angle ADC}{\sin \angle DAC}}}$

(2)

각도 ∠ ADB와 ∠ ADC는 선형 쌍을 형성하며, 즉 인접 보완각이다. 보조각은 같은 sine을 가지고 있기 때문에,

${\displaystyle {\sin \angle ADB}={\sin \angle ADC}.}$

각도 ∠ DAB와 ∠ DAC가 동일하다. 따라서 방정식 (1)과 (2)의 오른손은 같으므로 왼손도 같아야 한다.

${\displaystyle {\frac {BD }{CD }}={\frac {AB }{ AC },}$

그게 바로 각도 이등분 정리야

각도 ∠ DAB와 ∠ DAC가 동일하지 않으면 등식 (1)과 (2)를 다음과 같이 다시 쓸 수 있다.

${\displaystyle {{\frac {AB}{BD }\sin \angle \DAB}}각 \sin \angle ADB}$

${\displaystyle {{\frac { AC}{CD }\sin \angle \dAC=\sin \angle ADC}}$

각도 ∠ ADB와 ∠ ADC는 여전히 보조적이므로, 이러한 방정식의 오른손은 여전히 동일하므로, 우리는 다음을 얻는다.

${\displaystyle {{\frac {AB}{BD }}\sin \angle \angle \DAB={\frac { AC }{ CD }}\sin \angle \DAC}}}$

정리된 "정돈" 버전으로 재배열한다.

증명2길

D는 B나 C와 같지 않고 BC 선상의 점이며, AD가 삼각형 ABC의 고도가 아닌 점으로 하자.

B를₁ 삼각형 ABD에서 B까지 고도의 베이스(발)가 되게 하고 C를₁ ACD에서 C까지 삼각형에서 고도의 베이스가 되게 한다. 그렇다면 D가 B와 C사이에 엄밀하게 있으면 B나₁ C의₁ 하나와 하나만이 ABC 삼각형 안에 있고 B가₁ 하는 일반성을 잃지 않고 가정할 수 있다. 이 사례는 인접한 도표에 묘사되어 있다. D가 세그먼트 BC 외부에 있는 경우, B와₁ C₁ 모두 삼각형 안에 있지 않다.

∠ DBB와₁ ∠ DCC는₁ 직각인 반면, segment BDB와₁ ∠ CDC₁ 각도는 D가 세그먼트 BC(즉, B와 C 사이)에 놓여 있고, 고려되는 다른 사례에서 동일하므로 DBB와₁ DCC는₁ 유사(AAA)하므로 다음과 같은 것을 의미한다.

${\displaystyle {\frac {BD }{CD }}={\frac {BB_{1}{{1}{}}}}={\c_{1}{\frac { AB \sin \angle BAD}{AC \sin \sin \angle CAD}}}}}}}}}}}$

만약 D가 고도의 발이라면,

${\displaystyle {\frac {BD}{AB }}}}}{AB }}=\sin \angle \angle \bad{\text{ 및 }{\\frac { CD }}{ AC }}=\sin \angle \DAC,}}}$

일반화된 형태는 다음과 같다.

증명3길

$A{\displaystyle }$ ${\displaystyle A}$의 각도 이등분자가 만든$$${\displaystyle \mathrm{BA}}$ ${\displaystyle D}$ ${\displaystyle \triangle BAD}$ 및${\displaystyle \mathrm{}\mathrm{CA<img\; alt="\{\backslash displaystyle\; \backslash triangle\; BAD\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/47c0b72be8d84c1e7389d1448301c2527c9f416b"\; style="vertical-align:\; -0.338ex;\; width:7.497ex;\; height:2.176ex;">}}$ ${\displaystyle D}$ ${\displaystyle$ $\triangle CAD}$의 두 삼각형 면적의 비율을 보면 빠른 $증거$를 ${\displaystyle \mathrm{얻을}}$ 수 있다$.$$yle {\tfrac {1}{2}}gh}$ with base ${\displaystyle g}$ and altitude ${\displaystyle h}$ and ${\displaystyle {\tfrac {1}{2}}ab\sin(\gamma )}$ with sides ${\displaystyle a}$, ${\displaystyle b}$ and their enclosed angle ${\displaystyle \gamma }$, will yield the desired result.

$h{\displaystyle }$ ${\displaystyle h}$은(는) 기본 B ${\displaystyle C}${\$displaystyle$ BC$}$ 및 $\alpha {\displaystyle }$ ${\displaystyle \alpha}$의 삼각형 높이를 $A{\displaystyle }$ ${\displaystyle$ A$}$의 각도의 절반으로 표시한다$.$ 그런 다음

${\displaystyle {\frac{\triangle ACD}{{\frac {{}{1}{2}} BD h}{{\frac{1}{1}2}}: CD h}={\frac{BD}{{}}}}}}}}}}}$

그리고

${\displaystyle {\frac{\triangle ACD}{{\frac {{}{1}{2}}AB AD \sin(\alpha )}{{\frac {1}{1}{1}{1}}}}={\frac {AB}{}}}}}}}}}}}$

수확하다

${\displaystyle {\frac {BD}{ CD }}={\frac {AB}{ AC }}}.}$

외부 각도 이등분자

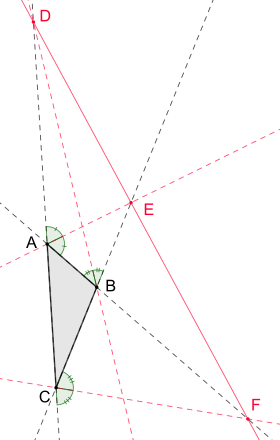
비등각 삼각형의 외부 각도 이등분자의 경우 삼각형 변의 길이 비율에 대해 유사한 방정식이 존재한다. 보다 정확하게는$A$의 외부 각도 이등분자가 $E{\displaystyle }$ ${\displaystyle E}$의 확장 측 B ${\displaystyle C}$ ${\displaystyle BC}$과 교차하는 경우$,$ $B{\displaystyle }$ ${\displaystyle B}$의 외부 각도 이등분자가 $D{\displaystyle }$ ${\displaystyle D}$의 확장 측 ${\displaystyle A}$ ${\disc}$과 외부 각도 이등분할 경우$또는{\displaystyle }$ C ${\displaystyle C}$에서 $F{\displaystyle }$ ${\displaystyle F}$의 확장면 ${\displaystyle \mathrm{AB}}$ ${\displaystyle AB}$을 교차한 다음 다음 방정식을 유지하십시오$.$^[1]

${\displaystyle {\frac { EB }{ EC }}={\frac { AB }{ AC }}}$, ${\displaystyle {\frac { FB }{ FA }}={\frac { CB }{ CA }}}$, ${\displaysty$$레 {\frac{DA}{DC }}={\frac {BA}{BC }}}}$

외부 각도 이등분선과 확장된 삼각형 면 $D{\displaystyle }$ ${\displaystyle$ D$\},$ $E{\displaystyle }$ ${\displaystyle E}$ und$$ $F{\displaystyle }$ ${\displaystyle F}$ 사이의 교차점 3개는 동일 선에 놓여 있는 것이다$$.^[2]

역사

각도 이등분자 정리는 유클리드 원소에서 6권 발의안 3으로 나타난다. 히스(1956, 페이지 197 (vol. 2)에 따르면, 파푸스가 증거 없이 이 결과를 가정했다는 점에 주목한 로버트 심슨에 의해 외부 각도 이등분자에 대한 해당 진술이 주어졌다. 히스는 이어 아우구스투스 드 모건이 두 진술을 다음과 같이 결합할 것을 제안했다고 한다.^[3]

만약 삼각형의 각도가 생산되는 반대쪽 또는 반대쪽을 절단하는 직선으로 내부 또는 외부에 이등분된다면, 그 측면의 세그먼트는 삼각형의 다른 면과 같은 비율을 가질 것이다; 그리고 삼각형의 한 면을 내부 또는 외부로 나누어 그것의 세그먼트가 다른 si와 같은 비율을 가질 것이다.삼각형의 데스, 단면점부터 단면점까지의 직선은 첫 번째 언급된 면과 반대되는 각점까지 그 각도에서 내부 또는 외부 각도를 이등분할 것이다.

적용들

이 섹션은 더 많은 정리/결과와 함께 확장되어야 한다. 덧셈으로 도움받을 수 있다(2020년 9월)

이 정리는 다음과 같은 이론/결과들을 증명하기 위해 사용되어 왔다.

• 삼각형 인센티브의 좌표

참조

추가 읽기

• G.W.I.S 아마라싱헤: 앵글 이등분자의 표준 길이와 앵글 이등분자의 정리, 고전 및 현대 기하학에 관한 글로벌 학술지 Vol 01(01) 페이지 15 – 27, 2012

외부 링크

• 각형 이등분자의 특성
• 칸 아카데미의 각도 이등분 정리 소개