곤도 효과

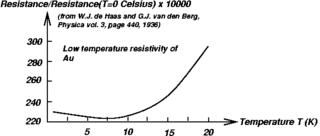
물리학에서 콘도 효과(Kondo effect)는 자성 불순물에 의한 금속 내 전도 전자의 산란을 설명하며, 그 결과 ^[1]온도에 따른 전기 저항률의 최소화를 초래한다.영향의 원인은 콘도 준(Jun Kondo)에 의해 처음 설명되었으며, 그는 불순물에 국소화된 d 궤도 전자로부터 s 궤도 전도 전자의 산란을 설명하기 위해 3차 섭동 이론을 문제에 적용하였다(콘도 모델).콘도의 계산에서는 온도가 0 ^[2]K에 가까워짐에 따라 산란률과 그에 따른 저항률이 로그적으로 증가할 것이라고 예측했습니다.1960년대 벨 연구소의 미리암 사라치크의 실험은 곤도 효과를 ^[3]입증하는 첫 번째 데이터를 제공했다.자기 불순물의 격자까지 확장되는 콘도 효과는 금속간 화합물, 특히 세륨, 프라시오디뮴, 이터뮴과 같은 희토류 원소와 우라늄과 같은 액티니드 원소와 관련된 무거운 페르미온과 콘도 절연체의 형성을 설명할 수 있습니다.콘도 효과는 양자 도트계에서도 관찰되고 있다.

이론.

콘도 효과를 포함한 $T$에 대한 저항률$\delta {\displaystyle }$(\$displaystyle\$$rho$$)$의 의존도는 다음과 같습니다.

$\displaystyle \rho (T)=\rho _{0}+aT^{2}+c_{m}\ln { frac { mu } { T } + bT ^ { 5 }$

여기서 ${\displaystyle {\theta \mathrm{}}_{}}$ 0$(\$ _${0})$은 잔류 저항률, $(\$는 페르미 액체의 성질을 나타내고, $T5{\displaystyle {}_{}}$$(\$$displaystyle$$$$bT$$^\{$$5})$는 격자 ${\displaystyle {진동}_{}}$의 영향을 나타낸다$.$$ystyle c_{m}$ $및$ μ {\$display$\mu$}$는 온도와 무관한 상수입니다.콘도 준은 온도에 대한 로그 의존성과 실험적으로 관찰된 농도 의존성을 가진 세 번째 항을 도출했다.

배경

콘도의 해법은 온도가 0 K에 가까워짐에 따라 발산되는 섭동 이론을 사용하여 도출되었지만, 이후의 방법들은 그의 결과를 정제하기 위해 비섭동 기술을 사용했다.이러한 개선은 유한한 저항률을 발생시켰지만 0이 아닌 온도에서 최소 저항의 특성을 유지했습니다.하나는 콘도 온도를 콘도 결과의 유효성을 제한하는 에너지 척도로 정의한다.앤더슨 불순물 모델과 그에 부수되는 윌슨식 재규격화 이론은 ^[4]문제의 근본적인 물리학을 이해하는 데 중요한 기여를 했다.슈리퍼-울프 변환에 기초하여, 콘도 모델은 앤더슨 불순물 모델의 강력한 결합 상태에 있는 것으로 나타났다.슈리퍼-울프 변환은^[5] Anderson 불순물 모델에서 높은 에너지 전하 들뜸을 투영하여 효과적인 해밀턴 모델로서 곤도 모델을 얻습니다.

콘도 효과는 점근 자유도의 예로서 생각할 수 있다. 즉, 저온과 저에너지에서 결합이 비섭동적으로 강해지는 상황이다.곤도 문제에서 결합은 국부적인 자기 불순물과 순회 전자 사이의 상호작용을 말합니다.

예

자기 이온 격자까지 확장되는 콘도 효과는 금속간 화합물, 특히 세륨, 프라시오디뮴, 이터뮴과 같은 희토류 원소들과 우라늄과 같은 액티니드 원소와 관련된 무거운 페르미온과 콘도 절연체의 형성을 설명할 수 있습니다.무거운 페르미온 물질에서 상호작용의 비교반적 성장은 자유 전자 질량의 수천 배까지 질량을 가진 준 전자로 이어진다. 즉, 상호작용에 의해 전자가 극적으로 느려진다.많은 경우에 그들은 초전도체이다.플루토늄의 ^{[citation needed]}특이한 금속 델타상을 이해하기 위해서는 곤도 효과의 징후가 필요하다고 생각된다.

콘도 효과는 양자 도트 ^[6][7]시스템에서 관찰되었습니다.이러한 시스템에서 적어도 1개의 비쌍전자를 가진 양자 닷은 자기 불순물로서 작용하며, 이 닷이 금속 전도 대역에 결합되면 전도 전자가 닷에서 산란할 수 있다.이것은 금속에 자성 불순물이 있는 전통적인 경우와 완전히 유사합니다.

콘도 절연체의 밴드 구조 하이브리드화와 플랫 밴드 토폴로지는 각도 분해형 광전자 방출 스펙트럼 ^[8][9][10]분석 실험에서 이미징되었다.

2012년 베리와 쿠퍼는 마요라나 ^[11]페르미온에서 위상학적 곤도 효과를 찾을 수 있다고 제안했고, 초강력 원자에 의한 양자 시뮬레이션도 그 ^[12]효과를 입증할 수 있을 것으로 보여졌습니다.

2017년에는 비엔나공과대학과 라이스대학 팀이 금속 세륨, 비스무트, 팔라듐으로 만든 신소재 개발에 대한 실험을 각각 실시했고, 이러한 구조의 모델을 실험하는 이론적 작업을 수행했다.실험 결과는 2017년 12월에^[13] 발표되었으며, 이론적 ^[14]연구와 함께 새로운 상태인 ^[15]상관 관계 중심 Weyl 세미메탈의 발견으로 이어졌다.연구팀은 이 새로운 양자 물질을 Weyl-Kondo 세미메탈이라고 명명했다.

레퍼런스

외부 링크

• 곤도 효과 - 발견 후 40년 - 일본물리학회지 특집호
• 무거운 페르미온에 대한 콘도 문제 - 콘도 효과에 관한 A.C.의 모노그래프.Hewson (ISBN 0-521-59947-4)
• 금속에 대한 이국적인 콘도 효과 - 특히 비자성 콘도 효과의 새로운 버전에 대한 모노그래프 (ISBN 0-7484-0889-4)
• 동적 평균장 그림 내 γ-플루토늄의 상관 전자, Nature 410, 793(2001).콘도 효과와 플루토늄의 연관성을 탐구하는 자연 기사