다면체 지도 투영법
Polyhedral map projection다면체 지도 투영법은 구면체 다면체에 기초한 지도 투영이다.일반적으로 다면체는 지구상에 겹쳐져 있으며, 다면체의 각 면은 평면에서 다각형이나 다른 모양으로 변환됩니다.가장 잘 알려진 다면체 지도 투영법은 벅민스터 풀러의 다이맥시온 지도입니다.구면 다면체 면이 평면상에 평평하게 놓이지 않고 일반 다면체의 면으로 변환되면, 그 결과는 다면체 [1]지구본이 됩니다.
종종 사용되는 다면체는 플라톤의 고체 또는 아르키메데스의 고체이다.그러나 다른 다면체도 사용할 수 있습니다.AuthaGraph 투영에서는 96개의 면을 가진 다면체를 사용하고 myriaheadle 투영에서는 임의의 수의 [2]면을 사용할 수 있습니다.면 사이의 인터럽트는 일반적이며 면의 수가 증가함에 따라 더 자주 발생하지만 일부 맵은 이를 피합니다. Lee Conformal 투영에는 경계에만 인터럽트가 있고 AuthaGraph 투영에는 내부 인터럽트가 없이 직사각형을 채우도록 면의 배율이 조정됩니다.일부 투영물은 테셀링되어 평면을 채울 수 있으며, 그 중 Lee 등각 투영도 있습니다.
어느 정도 다면체와 다면체의 각 면을 변환하는 데 사용되는 투영을 분리하여 생각할 수 있으며, 일부 투영을 다른 형태의 면에 적용할 수 있다.그노믹 투영법은 구면 다면체의 가장자리를 직선으로 변환하여 반구 내에 포함된 모든 다면체를 보존하기 때문에 일반적인 선택입니다.스나이더 등면적 투영법은 일반 [3]면이 있는 모든 다면체에 적용할 수 있습니다.Dynmaxion 맵의 이후 버전에서 사용된 투영법은 다른 등변 삼각형 면,[4] 심지어 특정 4변수로 [5]일반화할 수 있습니다.
다면체 지도 투영법은 사각형화된 구형 입방체 및 ISEA([6]Icosere Snyder Equal Area) 그리드와 마찬가지로 이산 글로벌 그리드를 작성하는 데 유용합니다.
역사
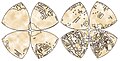
가장 먼저 알려진 다면체 투영법은 1514년 경 레오나르도 다빈치나 그의 동료에 의해 개발된 8면체 투영법으로, 8면체의 면을 렐레오 [1]삼각형으로 변형시킨다.
Christian Gottlieb Reichard는 1803년에 큐브를 바탕으로 다면체 지구본을 만들었습니다.이십면체 지구본은 1851년에 등장했다.골판지로 저렴하게 제작된 다면체 지구본은 유럽에서 [1]한때 인기가 있었다.
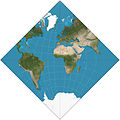
1879년 Peirce quincuncial 투영법, 1887년 Guyou-in-a-square 투영법, 1925년 Adams-반구-in-a-square 투영법과 함께 이면체에 기초한 투영법이 나타나기 시작했다.디헤드라는 전통적인 다면체는 아니지만 구면 다면체이며, 이러한 투영법에 사용되는 방법은 다른 다면체 투영법에도 사용됩니다.반구 사각형 투영법과 같은 작업에서 아담스는 지구 전체를 마름모꼴, 육각형,[7][8] 육각형으로 묘사하는 지도를 만들었습니다.
Bernard J. S. Cahill은 1909년에 팔면체에 기초한 "나비 지도"를 발명했다.이는 1975년 케힐-키즈 투영법과 1996년 워터맨 나비 투영법으로 일반화됐다.카힐의 작품은 풀러의 다이맥시온 지도에도 영향을 끼쳤다: 그의 첫 번째 버전은 정육면체를 기반으로 1943년에 출판되었고, 두 번째 버전은 20면체를 기반으로 1954년에 [1]출판되었다.
사각형화된 구형 입방체는 1975년 우주 배경 [9][10]탐사 프로젝트를 위해 고안되었다.
갤러리
「 」를 참조해 주세요.
레퍼런스
- ^ a b c d Pędzich, Paweł (2016-12-01). "Image of the World on polyhedral maps and globes". Polish Cartographical Review. 48 (4): 197–210. doi:10.1515/pcr-2016-0014. ISSN 2450-6966. S2CID 133013421.
- ^ van Wijk, Jarke J. (2008). "Unfolding the Earth: Myriahedral Projections". The Cartographic Journal. 45 (1): 32–42. doi:10.1179/000870408X276594. ISSN 0008-7041.
- ^ Snyder, John P (1992-03-01). "An Equal-Area Map Projection For Polyhedral Globes". Cartographica: The International Journal for Geographic Information and Geovisualization. 29 (1): 10–21. doi:10.3138/27H7-8K88-4882-1752. ISSN 0317-7173.
- ^ Crider, John E. (2008-03-01). "Exact Equations for Fuller's Map Projection and Inverse". Cartographica: The International Journal for Geographic Information and Geovisualization. 43 (1): 67–72. doi:10.3138/carto.43.1.67. ISSN 0317-7173.
- ^ Crider, John E. (2009-01-01). "A Geodesic Map Projection for Quadrilaterals". Cartography and Geographic Information Science. 36 (2): 131–147. doi:10.1559/152304009788188781. ISSN 1523-0406. S2CID 128390865.
- ^ Sahr, Kevin; White, Denis; Kimerling, A.J. (2003). "Geodesic discrete global grid systems" (PDF). Cartography and Geographic Information Science. 30 (2): 121–134. doi:10.1559/152304003100011090. S2CID 16549179.
- ^ Adams, Oscar S. (1925). Elliptic Functions Applied to Conformal World Maps. Issue 297 of United States Coast and Geodetic Survey Serial. U.S. Government Printing Office.
- ^ L.P. Lee (1976). "Conformal Projections based on Elliptic Functions". Cartographica. 13 (Monograph 16, supplement No. 1 to Canadian Cartographer).
- ^ Chan, F.K.; O'Neill, E. M. (1975). Feasibility Study of a Quadrilateralized Spherical Cube Earth Data Base (CSC - Computer Sciences Corporation, EPRF Technical Report 2-75) (Technical report). Monterey, California: Environmental Prediction Research Facility.
- ^ O'Neill, E. M. (1976). Extended Studies of a Quadrilateralized Spherical Cube Earth Data Base (PDF) (Technical report). Monterey, California: Environmental Prediction Research Facility. Archived (PDF) from the original on May 7, 2019.