3의 제곱근

3의 제곱근

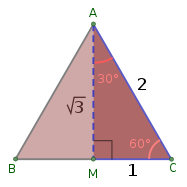
길이가 2인 삼각형의 높이는 3의 제곱근과 같다.
표현
십진법	1.7320508075688772935...
연속분수	${\displaystyle 1+{\properac {1}{1+{\properac {1}{1+{\properac {1}{1+{1+{1+\ddots }}}}}}}}}{1+}}}}}}$
이진수	1.10111011011001111010...
16진법	1.BB67AE8584CAA73B...

3의 제곱근은 그 자체로 곱하면 3이 되는 양의 실수다. 수학적으로 √3 또는 3으로^1/2 표기된다. 같은 성질을 가진 음수와 구별하기 위해 더 정확히 3의 주 제곱근이라고 한다. 3의 제곱근은 불합리한 수이다. 또한 비합리성을 입증한 키레네의 테오도로스의 뒤를 이어 테오도로스의 상수라고도 알려져 있다.

2013년 12월 현재, 십진법 표기의 수치는 최소 100억 자리 수로 계산되었다.^[1] 여기서 소수점 65자리까지 확장된 이 십진법은 OEIS: A002194에 의해 주어진다.

1.732050807568877293527446341505872366942805253810380628055806

분수 97/56(1.732142857...)을 근사치로 사용할 수 있다. 분모가 56에 불과함에도 불구하고 정확한 값과 1만분의 1(약 9.2×10⁻⁵) 미만 차이가 난다. 반올림 값 1.732는 실제 값의 0.01% 이내로 정확하다.

아르키메데스는 그 값의 범위를 다음과 같이 보고했다. (1351/780)²
> 3 > (265/153);^2
[2] 하한은 1/608400 (소수 6자리)에 정확하고 상한은 2/23409 (소수 4자리)에 정확하다.

표현.

지속분수[1, 2, 1, 2, 1, 2, 2, 1, …]로 표현할 수 있다(OEIS에서 순서 A040001).

그래서 이렇게 말하는 것은 사실이다.

${\displaystyle {\bmatrix}1&#2\\1&3\end{bmatrix}^{n}={\\\\n3}={\n3}={\\n3}a_{12}\a_{22}\end{bmatrix}}}}}}}}}}}}$

$그리고{\displaystyle }$ 나서 n${\displaystyle }$→${\displaystyle \mathrm{}}$∞ ${\displaystyle n\to \inflt }:$

${\displaystyle {\sqrt{3}}=2\cdot {\frac {a_{22}}{a_{12}}-1}$

또한 다음과 같은 일반화된 연속 분수를 통해 표현할 수 있다.

${\displaystyle [2;-4,-4,-4,-,...]=2-{\probac {1}{4-{\probac {1}{4-{4-\ddots }}}}}}$

즉, 매초마다 평가되는 [1, 1, 2, 1, 2, 1, …]이다.

지오메트리 및 삼각법

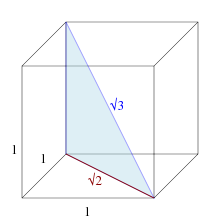
3의 제곱근은 지름 1의 원을 둘러싼 정삼각형의 다리 길이로 볼 수 있다.

길이 1의 변이 있는 정삼각형을 가로지르는 내부 각도를 양분하여 한 변과 직각을 이루면, 직각 삼각형의 하이포텐스는 길이 1이고, 옆면은 길이 1/2과 and3/2이다. 이로부터 60°의 삼각함수 탄젠트는 √3이고, 60°의 사인 및 30°의 코사인 둘 다 √3/2이다.

3의 제곱근은 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84°, 87°의 씨네를 포함한^[3] 다양한 다른 삼각 상수에 대한 대수적 표현에도 나타난다.

그것은 길이가 1인 일반 육각형의 평행한 면 사이의 거리다.

단위 큐브의 대각선 공간 길이 입니다.

vesica piscisis는 주요 축 대 부축 비율이 1:153이며, 이는 그 안에 2개의 정삼각형을 구성함으로써 알 수 있다.

기타 용도

동력공학

전력 공학에서, 3상 시스템에서 2상 사이의 전압은 중립 전압에 대한 라인의 3배와 같다. 그 이유는 어떤 두 상이라도 120°의 차이가 나며, 120°의 원 위에 있는 두 점이 반지름의 times3배만큼 분리되기 때문이다(위의 기하학적 예 참조).

참고 항목

• 2의 제곱근
• 5의 제곱근

메모들

참조

• S., D.; Jones, M. F. (1968). "22900D approximations to the square roots of the primes less than 100". Mathematics of Computation. 22 (101): 234–235. doi:10.2307/2004806. JSTOR 2004806.
• Uhler, H. S. (1951). "Approximations exceeding 1300 decimals for ${\displaystyle {\sqrt {3}}}$, ${\displaystyle {\frac {1}{\sqrt {3}}}}$, ${\displaystyle \sin({\frac {\pi }{3}})}$ and distribution of digits in them". Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443–447. doi:10.1073/pnas.37.7.443. PMC 1063398. PMID 16578382.
• Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers (Revised ed.). London: Penguin Group. p. 23.

외부 링크

위키미디어 커먼즈에는 3의 제곱근과 관련된 미디어가 있다.

• 테오도로스의 수학 세계에서의 상수
• [1] 케빈 브라운
• [2] E. B. 데이비스