대칭단면분류

In category theory, a branch of mathematics, a symmetric monoidal category is a monoidal category (i.e. a category in which a "tensor product" ${\displaystyle \otimes }$ is defined) such that the tensor product is symmetric (i.e. ${\displaystyle A\otimes B}$ is, in a certain strict sense, naturally isomorphic to ${\di$범주의 모든$$ 개체 $A{\displaystyle }$ ${\displaystyle A}$ 및 $B$ ${\displaystyle B}$에 대해$$ $splaystyle$ B$\otimes A}.$대칭 단면체 범주의 원형적 예 중 하나는 벡터 공간의 일반적인 텐서 곱을 사용하는 고정된 필드 k에 대한 벡터 공간의 범주다.

정의

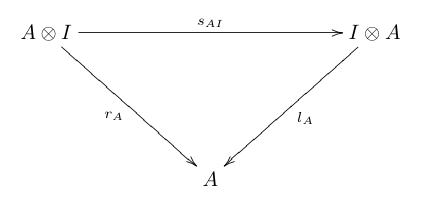
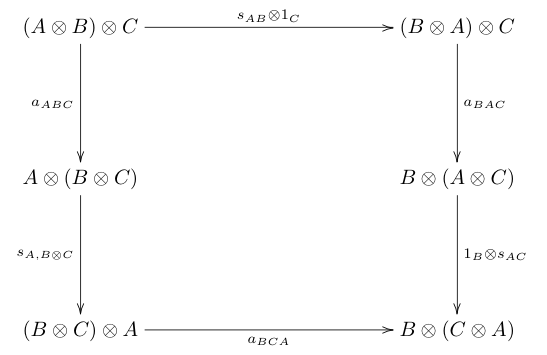
대칭 단면체 범주는 단면체 범주(C, ⊗, I)로서 C에 있는 물체의 모든 쌍 A, B에 ${\displaystyle {\mathrm{대해}}_{}}$ ${\displaystyle A_{}}$: ${\displaystyle A}$ ${\displaystyle \otimes }$ ${\displaystyle B}$→ ${\displaystyle B}$ ${\displaystyle \otimes }$ ${\displaystyle A}$ ${\displaystyle s_{$가 있다.$AB:$A$\$time $B\to B\time A}$이(가) A와 B에서 모두 자연스러우며, 다음과 같은 다이어그램이 통근한다.

• 장치 일관성:

  

• 연관성 일관성:

  

• 역 법칙:

  

위의 도표에서 a, l , r은 연관성 이형성, 왼쪽 단위는 이형성, 오른쪽 단위는 이형성이다.

예

대칭 단면체 범주의 일부 예와 비예:

• 집합의 범주.텐서 제품은 세팅된 이론적 카르테스 제품으로, 어떤 싱글톤이라도 유닛 오브젝트로 고정할 수 있다.
• 그룹의 범주.예전처럼 텐서 제품은 그룹의 데카르트 제품일 뿐이고, 사소한 그룹은 단위 객체다.
• 보다 일반적으로 유한한 제품을 가진 범주, 즉 데카르트 단면체 범주는 대칭 단면체다.텐서 제품은 객체의 직접 생산물이며, 모든 단자 객체(빈 제품)는 단위 객체다.
• 링 R에 대한 바이모듈의 범주는 단면체(모듈의 일반적인 텐서 제품을 사용)이지만 반드시 대칭인 것은 아니다.R이 역순인 경우, 왼쪽 R-모듈의 범주는 대칭 단면이다.후자의 예시 클래스는 주어진 필드에 걸친 모든 벡터 공간의 범주를 포함한다.
• 필드 k와 그룹(또는 k에 대한 리 대수)이 주어진 경우, 그룹의 모든 k-선형 표현 범주(또는 리 대수)는 대칭 단면체 범주다.여기서 표준 텐서 표현 제품을 사용한다.
• The categories (Ste,${\displaystyle \circledast }$) and (Ste,${\displaystyle \odot }$) of stereotype spaces over ${\displaystyle {\mathbb {C} }}$ are symmetric monoidal, and moreover, (Ste,${\displaystyle \circledast }$) is a closed symmetric monoidal category with the internal hom-functor ${\displaystyle$$\oslash$ $\}.$

특성.

대칭 단면체 범주의 분류 공간(신경의 기하학적 실현)은 $E{\displaystyle {}_{}}$ ${\displaystyle {\infty \mathrm{}}_{}}$ ${\$ 공간이기$$ 때문에 그룹 완성은 무한 루프 공간이다.^[1]

전문화

단도 대칭 단도 범주는 호환 가능한 단도 구조를 가진 대칭 단도 범주다.

코스모스는 완전한 닫힌 대칭 단면체 범주다.

일반화

대칭 단면체 범주에서 자연 이형체 $s{\displaystyle {}_{}}$ ${\displaystyle A_{}}$: ${\displaystyle A}$ ${\displaystyle \otimes }$ ${\displaystyle B}$→ ${\displaystyle B}$ ${\displaystyle \otimes }$ A ${\displaystyle s_{$$AB:A\otimes B\to B\oth A}$은(는) s ${\displaystyle B_{}{}_{}{}_{}}$ 1 ${\displaystyle {A1}_{}}$ B ${\$}라는 점에서 그들 자신의 inverses이다$$.$A}\circ s_{$$AB}=1_{A\otimes B$ 이 요구 조건을 포기하면(그러나 $여전히{\displaystyle }$ A${\displaystyle b}$ B ${\displaystyle$ A$\otimes$ B$}$는 ${\displaystyle B}$ ${\displaystyle \otimes }$ A ${\displaystyle$ B$\otimes$ A$}$에 대해 이형성이 있어야$$ 한다)$$ 우리는 단면체 범주에 대한 보다 일반적인 개념을 얻는다.

참조

• nLab의 대칭 단면체 범주
• 이 글에는 크리에이티브 커먼스 귀속/공유 알리크 라이센스에 따라 라이센스가 부여된 PlanetMath의 Symmetric 단면체 범주의 자료가 통합되어 있다.