자연 변형
Natural transformation수학의 한 분야인 범주 이론에서 자연적 변환은 관련된 범주의 내부 구조(즉, 형태론의 구성)를 존중하면서 한 펑터를 다른 것으로 변형시키는 방법을 제공한다. 따라서, 자연적 변환은 "환각자의 형태론"으로 간주될 수 있다. 실제로 이러한 직관은 소위 펑터 카테고리를 정의하기 위해 공식화될 수 있다. 자연적 변환은 범주 및 펑커 다음에 범주 이론의 가장 근본적인 개념 중 하나이며 결과적으로 대부분의 적용에 나타난다.
정의
과 G 이가) C 과 사이의 functor라면, F}에서 까지의 자연 변환 은 두 가지 요건을 충족하는 형태학군이다.
- The natural transformation must associate, to every object in , a morphism between objects of . The morphism is called the component of X{\X
- 요소는반드시 C {\ C의 모든 f : → Y {\f:X Y에 대해 다음을 가져야 한다.
마지막 방정식은 정류 도표로 쉽게 표현할 수 있다.
및 이(가) 모두 반대인 경우 이 다이어그램의 수직 화살표가 반전된다. {이(가) 에서 G G으)로 자연 변환된 경우 도 : → G{\ 또는 : G : 이 X G에서 모피즘 이라고 표현된다
모든 C{C\displaystyle}에서 만약, X{X\displaystyle}, 사상 η X{\displaystyle \eta_{X}}는 유질 동상에 D{D\displaystyle}, 그때 η{\displaystyle \eta}라고 하는 .mw-parser-output .vanchor>은 target~.vanchor-text{background-color:#b1d2ff}natural 동형 이성(혹은 가끔요. functors의 자연의 등가거나 동형 이성 cm이다. {\ 및 G 두 개의 functor displaystyle G}는 F displaysty F}에서 displaysty 까지의 자연 이형성이 있는 경우 자연 이형성 또는 이형성이라고 불린다
An infranatural transformation from to is simply a family of morphisms , for all in . Thus a natural transformation is an infranatural transformation for which for every morphism . The naturalizer of , nat, is the largest subcategory of conta 이(가) 자연적 변환으로 되는 C 의 모든 개체에서.
예
반대군
다음과 같은 진술
- "모든 집단은 상대 집단에 대해 자연적으로 이질성이 있다"
현대 수학이 풍부하다 우리는 이제 이 진술의 정확한 의미와 그 증거를 제시할 것이다. 그룹 동형성이 있는 모든 그룹 중 {\{\ 범주를 형태론으로 간주한다. If is a group, we define its opposite group as follows: is the same set as , and the operation is defined b = a{\ a op{\ G의 모든 승수는 "전환"된다. 동형성 : → 에서 = 를 정의하면 상대 그룹을 형성하는 것은 {\\\textbf{에 이르는 (공변량) f): f 은(는) G 에서 Hop {\H^{\op}}}}}에 이르는 집단 동형질화라는 점에 유의하십시오
위 문장의 내용은 다음과 같다.
- "ID functor : → {\{\ {은(는) 반대편 펑터 에 자연적으로 이형성이 있다.→
이를 증명하기 위해서는 이소모르프리즘 : → 그룹 G {\에 대해 G을(를) 적용하여 위의 다이어그램이 통근되도록 하십시오 G )= - 1 The formulas and show that is a group homomorphism with inverse 자연성을 증명하기 위해 동형성 f: → H f and show , i.e. for all in . This is true since 와 모든 그룹 동형사상에는 속성()- = (- 1) 가 있다
아벨리아화
그룹 을(를) 지정하면 우리는 아벨리아화 = / G,G 을(를) 정의 할 수 있다.렛트 G: → \displaystypi \은는 [, G {\G]}}}의 코세트에 투영 지도를 나타낸다 이 동음이의어는 "G 에서 자연적인 변환을 정의하고, 즉, 지금 우리가 확인하고 있다. 을(를) 그룹화하십시오. 모든 동형상 : → H 우리는 아벨 그룹으로의 동형질성은 정류자 하위 그룹을 죽이기 때문에 f 의 커널에 [, 이 포함되어 있다는 것을 알고 있다 Then factors through as for the unique homomorphism H . 이렇게 하면 : → functor 및 {\displaystyle }은(는) 자연적 변환이지만, ID functor에서 에 이르는 자연스러운 이형 변환은 아니다
후레위츠 동형성
후레위츠 동형체(Hurewicz homomorphism)를 예로 들며 대수적 위상에는 펑거트와 자연적 변환이 풍부하다. 임의의 뾰족한 위상학적 공간, ) 및 양의 정수 에 대해 그룹 동형성이 존재한다.
그 n{n\displaystyle}(X, x){\displaystyle(X,x)}의 -th 동위 그룹 X{X\displaystyle}의 n{n\displaystyle}-th 호몰 로지군까지 그 범주의 두π n{\displaystyle \pi_{n}}과 Hn{\displaystyle H_{n}}은 functors Top* 지적했다 위상 공간의 categ.o그룹의 ry Grp, n}}}}은(는) {\{n에서 {\n}}}}로 자연 변형된 것이다
결정인자
및 에 링 f :→ S 의 n n n 행렬 n( R) 및 은(는) n( ){\{\로 나타내는 동형체를 상속한다.각 매트릭스 항목에 을(를) 적용하여 얻은 마찬가지로 f은(는) 그룹 동형상 f: → S f로 제한한다. 여기서 는 R R의 단위 그룹을 . 실제로 GL 과(와)은(는) 정류 링 의 범주에서 {\{\까지의 functors이다 그룹 n ( ){\{\ R _{에 의해 표시된GL)}은는 집단 동형상이다.
,R {\ R에서 자연스럽다 결정 인자는 모든 링에 대해 동일한 공식으로 정의되기 때문에 = () .이(가) 버티고 있다. 이는 결정요인을 n { .
벡터 공간의 이중화
이(가) 필드인 경우, 벡터 V {\ 에 대해 벡터 으로부터 이중 이중으로 "자연적인" 주입 선형 V→ ∗{\ V가 있다. 이러한 지도는 다음과 같은 의미로 "자연"하며 이중 이중 이중 연산은 펑터(functor)이며, 지도는 신분 펑터(identity functor)에서 이중 이중 이중 펑터(double dual functor)로 자연 변환하는 구성 요소다.
유한 미적분학
모든 아벨 그룹 에대해 홈 , ( G)_{\G)})의 에서G {\ G의 기본 집합에 이르는 함수가 점으로 추가되는 아래 아벨 그룹 {\를 형성한다. (Here is the standard forgetful functor .) Given an morphism , the map given by left composing with the elements of the former is itself a homomorphism of abelian groups; in this way we obtain a functor . The finite difference operator taking each function to is a map from to itself, and the 이러한 맵의 컬렉션은 : Z→ Z 의 자연 변환을 제공한다
텐서홈접합
아벨 그룹 및 그룹 동음이의 범주 {\{\을(를) 고려하십시오. 모든 아벨 그룹 및 에 대해 그룹 이형성이 있음
- .
These isomorphisms are "natural" in the sense that they define a natural transformation between the two involved functors . (Here "op" is the opposite category of 에 있는 사소한 반대쪽 그룹 functor와 혼동하지 마십시오!)
이것은 공식적으로 텐서홈의 부속물이며, 부교감 한 쌍의 전형적인 예다. 자연적 변환은 부호화환자와 함께 자주 발생하며, 실제로 부호화환자는 어떤 자연 이형성에 의해 정의된다. 추가적으로, 모든 보조 기구의 쌍에는 단위와 상담이라고 불리는 두 개의 자연 변형(일반적으로 이소모르프리즘이 아님)이 장착되어 있다.
부자연 이형성
자연적 변환의 개념은 범주형이며, functor들 사이의 특정 지도가 전체 범주에 걸쳐 일관성 있게 수행될 수 있다는 상태(비공식적으로)이다. 비공식적으로, (전체 범주가 아닌) 개별 객체 사이의 특정 지도(esp. etsomorphism)를 "자연 이형성"이라고 부르는데, 이는 실제로 전체 범주에 정의되어 있다는 것을 암묵적으로 의미하며, functors의 자연스러운 변형을 정의한다; 이러한 직관을 공식화하는 것은 범주 t의 발달에 동기를 부여하는 요소였다.히리. 반대로 특정 물체 사이의 특정 지도를 전체 범주의 자연적 변환으로 확대할 수 없다면 부자연스러운 이형성(또는 "이형성은 자연스럽지 않다")이라고 부를 수도 있다. Given an object a functor (taking for simplicity the first functor to be the identity) and an isomorphism proof of unnaturality is most easily shown by giving an automorphism that는 이러한 이형성(그래서 G ) η η η η η η { { {{ { { \ \ \ \ \ \G(A)\ \eta \ \ } }} 보다 강력하게, 이소모르프리즘과 관련 없이 X 과 G( ) 이(가) 자연적으로 이소모르프성이 아님을 증명하고 싶다면, 이소모르프리즘 에 대해 통근하지 않는 일부 {\\}이 있음을 보여야 한다.e 사례 은(는) 모든 후보 이형성 에 대해 작동하며, 다른 경우에는 각 이형성에 대해 다른 A 을(는) 구성하는 방법을 보여 주어야 한다. 범주의 지도는 중요한 역할을 한다. 예를 들어, 지도만이 신원 지도일 경우, 어떠한 비인륜적 변환도 자연스러운 것이다.
이는 그룹 이론이나 모듈 이론의 개념과 유사하지만(그러나 좀 더 범주적), 즉, 대상을 직접 합으로 분해하는 것이 "자연적이지 않다" 또는 "독특하지 않다"는 개념들과 유사하다. 즉, 직접 합 분해를 보존하지 않는 자동화가 존재하기 때문에 – 주요 이상적 영역 § 유니크에 걸쳐 정밀하게 생성된 모듈에 대한 구조 정리를 참조한다.예를 들면 우니티
일부 저자들은 자연 이형성에는 을(를) 사용하고, 부자연스러운 이형성에는 {\\약을(를) 사용하여 합리적으로 구분하고, 평등(보통 지도 평등)에는 = {\
예: 토러스 기본 그룹
functorial 문과 개별 객체의 구별의 예로서 제품 공간의 호모토피 그룹, 특히 토러스 기본 그룹을 고려한다.
The homotopy groups of a product space are naturally the product of the homotopy groups of the components, with the isomorphism gi기본적으로 제품 공간으로의 맵은 정확히 구성요소에 대한 맵의 산물이기 때문에 두 요소에 투영함으로써 ven은 functorial 문장이다.
However, the torus (which is abstractly a product of two circles) has fundamental group isomorphic to , but the splitting is not natural. \ 약 및= [a] 사용법에 유의하십시오.
This abstract isomorphism with a product is not natural, as some isomorphisms of do not preserve the product: the self-homeomorphism of (thought of as the quotient space ) given by 가역 정수 매트릭스의 이 매트릭스로 Z2에Aystyle \left({\begin{}smallmatrix 1&, 1\\0&, 1\end{smallmatrix}}\right)}(하나를 개방 곡선의 기하학적으로 한 덴 트위스트)행위{\displaystyle \mathbb{Z}^{2}}(그것이 전체적인 선형 군 GL(Z, 2에 있어요){\displaystyle{\text{GL}}(\mathbb{Z},2)}.), 대각선이 아니기 때문에 분해물을 생산물로 보존하지 않는다. However, if one is given the torus as a product – equivalently, given a decomposition of the space – then the splitting of the group follows from the general statement earlier. 범주형 용어로 관련 범주(제품 공간의 구조 보존)는 "제품 공간의 맵, 즉 각 구성 요소 간의 맵 쌍"이다.
자연성은 범주형 개념이며, 어떤 데이터가 주어지는지에 대해 매우 정밀해야 한다. 즉, 제품이 될 수 있는 공간으로서의 토러스(공간과 연속 지도의 범주)는 하나의 제품으로 제시된 토러스(두 공간의 제품 범주 및 각 구성 요소 사이의 연속 지도의 범주에서)와 다르다.
예제: 유한 차원 벡터 공간의 이중화
모든 유한차원 벡터 공간은 그것의 이중 공간과 이형이지만, 두 공간 사이에는 많은 다른 이형성이 있을 수 있다. 유한차원 벡터 공간과 그것의 이중 공간 사이에는 일반적으로 자연 이형성이 없다.[1] 그러나 관련 범주(지도에 추가적인 구조와 제약이 있는 경우)는 아래에 기술된 바와 같이 자연적인 이형성을 가진다.
유한 차원 벡터 공간의 이중 공간은 다시 같은 차원의 유한 차원 벡터 공간이며, 따라서 이러한 공간들은 이형성이며, 이는 차원이 주어진 장에 걸쳐 유한 차원 벡터 공간의 유일한 불변성이기 때문이다. 그러나 추가적인 제약조건(예: 지도는 선택된 근거를 보존하는 요건)이 없는 경우, 공간으로부터 그 이중으로 가는 지도가 고유하지 않기 때문에 그러한 이형성은 선택이 필요하며, "자연스럽지 않다"는 것이다. 유한차원 벡터 공간과 선형 지도의 범주에서는 각 공간에 대한 이소형성(예를 들어 모든 벡터 공간의 기초를 선택하고 그에 상응하는 이소형성을 취함)을 선택함으로써 벡터 공간으로부터 이중으로 인트라나토럴 이소형성을 정의할 수 있지만, 이것이 자연적 변환을 정의하지는 못할 것이다. 직관적으로 이것은 그러한 이형질성의 선택은 제로맵과 통용되지 않기 때문에 엄격한 선택이 필요했기 때문이다. 자세한 논의는 (Mac Lane & Birkhoff 1999, §VI.4)를 참조한다.
유한차원 벡터 공간(물체로서의)과 정체성 및 이중 펑터(dual functors)에서 시작하여 자연 이소모르퍼시즘을 정의할 수 있지만, 이를 위해서는 먼저 구조를 추가한 다음, 지도를 "모든 선형 지도"에서 "이 구조를 존중하는 선형 지도"로 제한해야 한다. Explicitly, for each vector space, require that it comes with the data of an isomorphism to its dual, . In other words, take as objects vector spaces with a nondegenerate bilinear form . This defines an infr아나토럴 이형성(각 물체에 대한 이형성). 그런 다음 는 : V→ 만 이등유형으로 통근하도록 제한한다. or in other words, preserve the bilinear form: . (These maps define the naturalizer of the isomorphisms.) 결과 범주는 비탈면 이선형 형태의 유한차원 벡터 공간과 이선형 형태를 존중하는 선형 변환을 맵핑하는 것으로, 시공에 의해 정체성에서 이중으로 자연 이형성(각 공간은 이중으로 이형성을 가지며, 범주에 있는 지도는 통근해야 한다)이 있다. 이러한 관점에서 보면, 이 구조는 완전히 일반적이며, 벡터 공간의 특정한 특성에 의존하지 않는다.
이 범주(비분해형 이선형 형태의 마무리 차원 벡터 공간, 이선형 형태를 존중하는 선형 변환 맵)에서 벡터 공간 사이의 지도의 이중은 전치형으로 식별할 수 있다. 종종 기하학적 관심 때문에 이것은 하위 범주에 특화되어 있는데, 비분열 이선형 형태는 대칭적(직교적 행렬), 대칭적 및 양정확정적(제품 공간 내부), 대칭적 sesquilinar(헤르미티아 공간), 대칭 대칭적 및 완전 등방성(심플렉티)과 같은 추가 특성을 갖도록 요구하기 때문이다.c 벡터 공간) 등 – 이 모든 범주에서 벡터 공간은 자연적으로 비디제너레이션 이선형 형태로 이중으로 식별된다.
자연적 변환을 통한 운영
: → {\ and are natural transformations between functors , then we can compose them to get a natural transformation 이 은 구성 요소별로 수행된다: ( ) X= X
자연적 변환의 이러한 "수직적 구성"은 연관성이 있고 정체성이 있으며, 모든 펑터 → D의 수집 자체를 범주로 간주할 수 있다(Functor 범주 아래 참조).
자연적 변환은 또한 "수평적 구성"을 가지고 있다. : → {\은(는) , : → D D 및 : → :은는) J , : D→ {\ J 사이의 자연스러운 변형이다. E 그런 다음 functors의 구성을 통해 자연 변환 composition : → G : 서 ( ) = G( X) J ( )
이 수술은 또한 정체성과 연관성이 있으며, 그 정체성은 수직 구성의 그것과 일치한다. 두 연산은 수직적 구성을 수평적 구성과 교환하는 아이덴티티(identity)에 의해 관련된다: 만약 우리가 오른쪽에 보이는 것과 같이 4개의 자연적 변환 , 을 가지고 있다면, 다음과 같은 아이덴티티가 유지된다.
: → {\은(는) , G : → D[\ FG:와 H : D→ H 사이의 스러운 변형이다.는 또 다른 functor로, 그러면 자연 변환 H : → : HG
반면에 : → K은(는) 펑터(functor)로, 자연 변형 K: → 은(는) 다음을 통해 정의됨
펑터 범주
이(가) 범주이고 I I}이) 작은 범주라면 펑터 범주 은(는) 에서 까지의 모든 functor를 객체로 하고 그 functor들 사이의 자연적 변환을 형태적으로 가지고 있다. 이는 모든 functor {\에 대해 ID 변환 1 :F → {\ 1_ 객체 에 대한 ID 형태론( Morphism F과 두 개의 자연적 변환(위의 "수직적 구성")의 구성도 다시 자연적 변환이다.
I C의 이형성은(는) 정확히 자연 이형이다. 즉, 자연적 변환 : → G : is a natural isomorphism if and only if there exists a natural transformation such that and .
펑터 범주 C은(는) 방향 그래프에서 이(가) 발생할 경우 특히 유용하다. 예를 들어, }이(가) 방향 그래프 범주 • → • C은는 C {\의 형태론과 : → V {\: 사이의 형태론을 대상으로 한다. 및 : X→ 의 I C은 f :→ X 및 : → Y 의 에 "제곱이 통근됨 즉 = g \ \\ f=
보다 일반적으로, 2-카테고리 을(를) 구축할 수 있다.
- 0-118(수치)은 작은 범주,
- 두 물체 과 사이의 1-셀(화살표)은 에서 D 까지의 functors이다
- 두 개의 1-셀 사이의 2-셀(기능자) : → D F 및 : → D 은(는) 에서 으)로 자연 변환된 것이다
수평과 수직의 구성은 앞에서 설명한 자연 변형 사이의 구성이다. 펑터 범주 C I은(는) 이 범주에서 간단히 홈 범주가 된다(소규모 문제는 제쳐두고).
더 많은 예
모든 한계와 콜리밋은 원뿔이 대각선 펑터를 도메인으로 하는 자연적 변환에 해당하므로 단순한 자연적 변환의 예를 제공한다. 실제로 한계와 콜리미트가 보편적 속성의 관점에서 직접 정의된다면, 그것들은 펑터 범주에서 보편적 형태론이다.
요네다 보조정리
이(가) 로컬로 작은 C{\의 개체인 경우 Y C( , Y) Y은(는) 공변량 F: → 를 정의한다. 이 functor를 표현형이라고 한다(더 일반적으로 functor는 X {\의 적절한 선택을 위해 이 functor와 자연적으로 이형성인 functor이다). 표현 가능한 functor에서 임의 functor C → 은(는) 완전히 알려져 있고 설명하기 쉽다. 이것이 요네다 보조정리기의 내용이다.
역사 노트
카테고리 이론의 창시자 중 한 명인 손더스 맥 레인은 "나는 펑커를 연구하기 위해 카테고리를 만든 것이 아니라 자연적 변환을 연구하기 위해 범주를 발명했다.[2] 집단의 연구가 동형문학의 연구 없이는 완성되지 않는 것처럼 범주의 연구도 펑커스의 연구 없이는 완성되지 않는다. 맥레인이 이렇게 말하는 이유는 자연 변형 연구 없이는 펑커 연구 자체가 완성되지 않기 때문이다.
맥 레인의 발언의 맥락은 호몰로지라는 자명한 이론이었다. 동질학을 구성하는 다른 방법들이 일치한다는 것을 보여줄 수 있다. 예를 들어, 단순화된 복합체의 경우, 그 집단이 직접 정의한 집단은 단수 이론의 집단과 이형화될 것이다. 자연적 변환의 언어 없이는 쉽게 표현할 수 없는 것은 호몰로지 집단이 물체들 사이의 형태론과 어떻게 양립할 수 있는가 하는 것과, 같은 호몰로지 이론이 어떻게 같은 호몰로지 집단을 가질 뿐만 아니라, 그 집단들 간의 형태론도 어떻게 동일한가 하는 것이다.
참고 항목
메모들
- ^ Z는n Z의 n-폴드 제품 또는 Z와n − 1 미묘하게 다른 세트로 정의될 수 있다(자연스럽게 식별할 수 있지만, ≅으로 표기될 수 있다). 여기서 정의를 고쳤는데, 어떤 경우에도 n = 2와 일치한다.
참조
- ^ (Mac Lane & Birkhoff 1999, §VI.4)
- ^ (Mac Lane 1998, §I.4)
- Mac Lane, Saunders (1998), Categories for the Working Mathematician, Graduate Texts in Mathematics 5 (2nd ed.), Springer-Verlag, p. 16, ISBN 0-387-98403-8
- Mac Lane, Saunders; Birkhoff, Garrett (1999), Algebra (3rd ed.), AMS Chelsea Publishing, ISBN 0-8218-1646-2.
- Awodey, Steve (2010). Category theory. Oxford New York: Oxford University Press. p. 156. ISBN 978-0199237180.
- Lane, Saunders (1992). Sheaves in geometry and logic : a first introduction to topos theory. New York: Springer-Verlag. p. 13. ISBN 0387977104.
외부 링크
- n-범주적 관점을 중심으로 한 수학, 물리학, 철학에 관한 위키 프로젝트인 nLab
- 안드레 조이알, 캣랩(CatLab)은 범주형 수학의 전시에 전념하는 위키 프로젝트다.
- Hillman, Chris. "A Categorical Primer". CiteSeerX 10.1.1.24.3264:
{{cite web}}: 카테고리 이론에 대한 누락 또는 빈(도움말) 형식 소개. - J. 아다멕, H. 에를리히, G. 스테커, 추상적이고 구체적인 범주-고양이의 기쁨
- 스탠포드 철학 백과사전: 장 피에르 마르키스의 "카테고리 이론". 광범위한 참고 문헌 목록.
- 범주론 학술회의 목록
- 배즈, 존 1996 "N-카테고리 이야기" 상위 범주에 대한 비공식 소개.
- WildCats는 Mathematica의 카테고리 이론 패키지다. 물체의 조작 및 시각화, 형태론, 범주, 펑터, 자연 변형, 범용 특성.
- 카테고리 이론에 대한 유튜브 채널인 캣스터.
- 범주, 논리 및 물리학의 기초와 관련된 녹화된 대화의 비디오 보관.
- 유한 집합 범주에 범주형 구성의 예를 생성하는 대화형 웹 페이지.
 G
G 






 모든
모든 

















 대해
대해 









![[G,G]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ddf7a724a331d1e12ffa6571ba246ebf08f1335)
















 링
링 







 (는) 정류 링
(는) 정류 링 



 (가) 버티고 있다. 이는 결정요인을
(가) 버티고 있다. 이는 결정요인을 
 대해 벡터
대해 벡터  이중
이중














 대해 그룹 이형성이 있음
대해 그룹 이형성이 있음 





 (가) 자연적으로 이소모르프성이 아님을 증명하고 싶다면, 이소모르프리즘
(가) 자연적으로 이소모르프성이 아님을 증명하고 싶다면, 이소모르프리즘  대해
대해












 이등유형으로 통근하도록 제한한다.
이등유형으로 통근하도록 제한한다. 






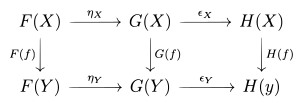




 (
(
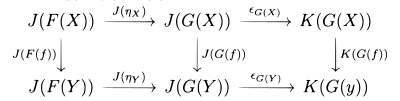


 또 다른 functor로, 그러면 자연 변환 H
또 다른 functor로, 그러면 자연 변환 H


 (는) 다음을 통해 정의됨
(는) 다음을 통해 정의됨 
 펑터
펑터 










 (를) 구축할 수 있다.
(를) 구축할 수 있다. 







