자전거 및 오토바이 동력학

자전거와 오토바이 역학은 자전거와 오토바이 그리고 자전거에 작용하는 힘 때문에 자전거와 오토바이의 운동과 그 구성품들에 대한 과학이다.역학은 고전역학으로 알려진 물리학의 한 분과에 속한다.자전거의 관심 운동에는 밸런싱, 조향, 제동, 가속, 서스펜션 작동 및 진동이 포함된다.이러한 운동에 대한 연구는 19세기 후반에 시작되어 오늘날에도 계속되고 있다.^[1][2][3]

자전거와 오토바이는 둘 다 단일 트랙 차량이기 때문에 이들의 동작은 많은 기본적 속성이 공통적으로 있으며 다륜, 삼륜, 사륜차 등 바퀴 달린 다른 차량과는 근본적으로 다르고 공부하기 어렵다.^[4]외발자전거와 마찬가지로 자전거는 정차 시 측면 안정성이 떨어지고, 대부분의 상황에서는 앞으로 이동할 때만 직립 상태를 유지할 수 있다.실험과 수학적 분석은 자전거가 바퀴 위로 질량의 중심을 유지하기 위해 조향되었을 때 똑바로 서 있다는 것을 보여주었다.이 조향은 일반적으로 승차자 또는 특정 상황에서 자전거 자체에 의해 공급된다.기하학, 질량 분포 및 자이로스코프 효과를 포함한 몇 가지 요인은 모두 이러한 자기 안정성에 다양한 정도에 기여하지만, 오랜 가설과 주장, 자이로스코프나 트레일과 같은 어떤 단일 효과가 안정화 힘에 전적으로 책임이 있다는 것은 불명확한 것이다.^[1][5][6][7]

똑바로 서 있는 것이 초보 탑승자의 주된 목표일 수 있지만, 자전거는 한 바퀴 회전 시 균형을 유지하기 위해 기울어져야 한다: 속도가 높거나 회전 반경이 작을수록 더 기울어져야 한다.이것은 중력과의 턴으로 인해 원심력에 의해 생성된 휠 접촉 패치에 대한 롤 토크의 균형을 맞춘다.이 기울기는 보통 반대 방향의 순간적인 조향에 의해 생성되는데, 역스티어링이라고 한다.역스티어링 기술은 보통 의식적인 사고보다는 모터 학습에 의해 습득되고 절차적 기억력을 통해 실행된다.다른 바퀴 달린 차량과 달리 자전거의 1차 제어 입력은 위치가 아닌 조향 토크다.^[8]

정지해 있을 때 종방향으로 안정적이긴 하지만 자전거는 충분한 가속이나 감속 하에서 지상에서 바퀴를 들어올릴 수 있을 정도로 질량의 중심이 높고 휠베이스가 짧다.제동 시, 앞바퀴가 지면에 닿는 지점과 관련하여 자전거와 승차자의 질량 중심 결합 위치에 따라, 그리고 앞 브레이크를 충분히 세게 밟으면 자전거는 충돌의 원인이 될 수 있는 앞바퀴를 미끄러뜨리거나 앞바퀴 위로 자전거와 승차자를 뒤집는다.가속하는 동안에도 유사한 상황이 가능하지만, 후륜과 관련된 경우도 있다.^{[9][self-published source?]}

역사

자전거 역학 연구의 역사는 자전거 자체만큼이나 오래되었다.랭킨, 호칭, 위플과 같은 유명한 과학자들의 기여를 포함한다.^[2]19세기 초, 로프마스치네, 벨로키페데, 드라이신, 댄디 말이라고 다양하게 불리는 이륜차를 발명한 공로를 인정받은 카를 폰 드라이스는 기수가 앞바퀴를 조종함으로써 기계의 균형을 맞출 수 있다는 것을 보여주었다.^[2]1869년 랭킨은 '엔지니어'에 기댄 방향으로 조종함으로써 균형을 유지한다는 폰 드라이스의 주장을 되풀이하는 기사를 실었다.^[10]

1897년 프랑스 과학 아카데미는 Free Fourneyron 대회의 목표를 자전거의 역동성에 대한 이해로 정했다.따라서 19세기 말까지 카를로 부르레, 에마뉘엘 카르발로, 프란시스 휘플은 일부 안전자전거가 올바른 속도로 움직이면 실제로 균형을 잡을 수 있다는 것을 강체-신체역학으로 보여주었다.^[2]부르레는 프릭스 포니론상을, 휘플은 케임브리지대 스미스상을 수상했다.^[7]이것을 가능하게 하는 데 도움이 되는 수직에서 조향축을 기울이는 것에 대해 누가 공로를 인정해야 하는지는 명확하지 않다.^[11]

1970년에 데이비드 E. H. 존스는 자전거의 균형을 맞추기 위해 자이로스코프 효과가 필요하지 않다는 것을 보여주는 기사를 물리학 투데이에 발표했다.^[6]1971년, 그가 흔들림, 짜임, 전복 모드를 확인하고 이름을 붙였을 때,^[12] 로빈 샤프는 정기적으로 오토바이와 자전거의 행동에 대해 글을 썼다.^[13]런던 임페리얼 칼리지에 재학 중인 그는 데이비드 라임베어, 시모스 에반게루와 함께 일했다.^[14]

1970년대 초, 코넬 항공 연구소(CAL, 후기 미국 뉴욕 버팔로의 칼스판 주식회사)는 자전거와 오토바이 역학을 연구하고 시뮬레이션하기 위해 슈윈 자전거 회사 등의 후원을 받았다.이 작업의 일부는 현재 대중에게 공개되었고 30개 이상의 상세 보고서에 대한 스캔들이 이 TU Delft Bicycle Dynamics 사이트에 게시되었다.

1990년대 이후, 코살터 외 연구진은 파도바 대학에서 오토바이 역학을 연구해왔다.그들의 연구는 실험과 수치 모두 짜임,^[15] 흔들림,^[16] 수다,^[17] 시뮬레이터,^[18] 차량 모델링,^[19] 타이어 모델링,^[20][21] 핸들링 ^[22][23]및 최소 랩 타임 조작을 다루었다.^[24][25]

2007년 메이자드 외 연구진은 두 가지 다른 방법에 의한 검증과 함께 왕립학회 A의 의사록에 표준 선형화된 운동 방정식을 발표했다.^[2]이 방정식들은 타이어가 미끄러지지 않고 굴러가는 것으로 가정했다. 즉, 타이어가 가리키는 곳으로 가고, 라이더가 자전거의 뒷골격에 단단히 부착되는 것으로 가정했다.

2011년 쿠이즈만 외 연구진은 사이언스에 자전거가 균형을 잡으려면 자이로스코프 효과도, 트레일에 의한 캐스터 효과도 필요하지 않다는 기사를 실었다.^[1]그들은 부정적인 트레일이 있어도 동작 방정식이 스스로 안정될 수 있고, 앞 바퀴가 조향 축 앞 지면에 닿으며, 역회전 바퀴가 있어 자이로스코프 효과를 취소할 수 있는 2개의 질량 스케이트 자전거를 설계했다.그리고 나서 그들은 그 예측을 검증하기 위해 물리적 모델을 만들었다.이를 위해 조향 기하학 또는 안정성에 대해 아래에 제공된 세부 사항 중 일부를 재평가해야 할 수 있다.자전거 역학은 디스커버의 2011년 100대 탑스토리 중 26개로 선정되었다.^[26]

2013년에 Eddy Merckx Cycles는 겐트 대학교와 함께 자전거 안정성을 검사하기 위해 15만 유로가 넘는 상금을 받았다.^[27]

폭력

자전거와 승차자가 단일 계통으로 간주되는 경우, 시스템과 그 구성 요소에 작용하는 힘은 대략 내부와 외부의 두 그룹으로 나눌 수 있다.외력은 중력, 관성, 지반과의 접촉, 대기와의 접촉에 기인한다.내부 힘은 승차자와 구성 요소 간의 상호작용에 의해 발생한다.

외력

모든 질량과 마찬가지로 중력은 승차자와 자전거 부품을 지구 쪽으로 당긴다.각 타이어 접점에는 수평 및 수직 구성 요소 모두에 대한 접지 반력이 있다.수직 구성 요소는 대부분 중력에 대항하지만 제동 및 가속에도 따라 달라진다.자세한 내용은 아래 세로 안정성 섹션을 참조하십시오.바퀴와 지면의 마찰로 인해 회전저항을 포함한 수평부품은 추진력, 제동력, 회전력에 반응한다.대기에 의한 공기역학적 힘은 대부분 드래그 형태지만, 역풍에서 오는 경우도 있다.평탄한 지면에서 정상적인 자전거 주행 속도에서 공기역학적 드래그는 전방 운동에 저항하는 가장 큰 힘이다.^{[28]: 188} 더 빠른 속도에서 공기역학적 드래그는 전방 운동에 저항하는 압도적으로 가장 큰 힘이 된다.

이동 방향만 바꾸는 것 외에 균형을 잡기 위한 기동 중에 회전력이 발생한다.이러한 힘은 자전거와 승차자의 가속 기준 프레임에서 원심력으로 해석되거나, 단순히 정지된 관성 기준 프레임에서 관성으로 해석될 수 있으며, 전혀 힘이 아니다.바퀴, 엔진, 변속기 등 회전하는 부품에 작용하는 자이로스코프 힘도 회전하는 부품들의 관성 때문이다.그것들은 아래의 자이로스코프 효과에 관한 섹션에서 자세히 논의된다.

내력

자전거와 라이더 시스템의 구성 요소들 사이의 내부 힘들은 대부분 승차자 또는 마찰에 의해 발생한다.페달을 밟는 것 외에도, 승차자는 조향 메커니즘(프론트 포크, 핸들 바, 프론트 휠 등)과 후면 프레임 사이에 토크를 적용할 수 있다.마찰은 구동렬, 조향 메커니즘 및 후면 프레임 등 서로 반대 방향으로 움직이는 모든 부품 사이에 존재한다.회전하는 바퀴와 회전하지 않는 프레임 부품 사이에 마찰을 일으키는 브레이크 외에도 많은 자전거가 앞뒤의 서스펜션을 가지고 있다.일부 오토바이와 자전거는 바람직하지 않은 운동에너지를 발산하기 위한 조향 댐퍼가 있고,^[14][29] 일부 자전거는 앞쪽 포크와 프레임을 연결하는 스프링이 있어 자전거를 직진하는 경향이 있는 점진적인 토크를 제공한다.후방 서스펜션이 있는 자전거에서 구동렬과 서스펜션 사이의 피드백은 설계자가 다양한 연결 구성과 댐퍼로 처리하려고 시도하는 문제다.^[30]

동작

자전거의 동작은 대칭 중심면에서 벗어난 동작(측면)과 대칭 중심면에 있는 동작(종방향 또는 수직)으로 대략 분류할 수 있다.측면 동작은 균형잡기, 기울기, 조향, 회전을 포함한다.대칭의 중심면에서의 동작은 물론 앞으로 굴러가는 동작도 포함하지만 정지, 바퀴, 브레이크 다이빙, 그리고 대부분의 서스펜션 작동도 포함한다.이 두 그룹의 동작은 선형적으로 분리된다. 즉, 그들은 첫 번째 순서로 서로 상호작용하지 않는다.^[2]제어되지 않은 자전거는 정지해 있을 때 횡방향으로 불안정하며, 올바른 조건에서 이동하거나 승차자가 조종할 때 횡방향으로 스스로 안정될 수 있다.반대로 자전거는 정지할 때 종방향으로 안정적이며 충분한 가속이나 감속을 거쳤을 때 종방향으로 불안정해질 수 있다.

횡역학

둘 중 횡방향 역학은 보다 복잡하다는 것이 입증되어 최소 두 개의 일반화된 좌표와 함께 3차원 다중역학 분석이 필요하다.주 운동을 포착하기 위해서는 최소한 두 개의 결합된 2차 미분 방정식이 필요하다.^[2]정확한 해법은 불가능하며, 대신 수치적 방법을 사용해야 한다.^[2]자전거 균형에 대한 경쟁적인 이론들은 인쇄물과 온라인에서 여전히 발견된다.반면에, 후기 절에서 보여지듯이, 많은 종방향 동적 분석은 평면 운동학 및 하나의 좌표만으로 간단히 이루어질 수 있다.

잔액

자전거 균형에 대해 논의할 때, 「안정성」, 「자기 안정성」, 「제어성」을 주의 깊게 구별할 필요가 있다.최근의 연구는 "라이더 제어 자전거의 안정성은 실제로 자전거의 자기 안정성과 관련이 있다"^[1]고 시사한다.

자전거는 조향할 때 직립 상태를 유지하여 지반 반응력이 경험하는 다른 모든 내적 및 외적 힘의 균형을 정확히 유지하는데, 예를 들어 기울일 경우 중력, 회전할 경우 관성 또는 원심, 조향될 경우 자이로스코프, 역풍일 경우 공기역학 등이 그것이다.^[28]조향은 승차자 또는 특정 상황에서 자전거 자체에 의해 공급될 수 있다.^[31]이러한 자기 안정성은 자전거의 기하학, 질량 분포 및 전방 속도에 따라 달라지는 여러 효과의 조합에 의해 생성된다.타이어, 서스펜션, 스티어링 댐핑 및 프레임 플렉스도 영향을 미칠 수 있으며, 특히 오토바이의 경우 더욱 그러하다.

비교적 움직이지 않고 있을 때에도, 승차자는 같은 원리로 자전거의 균형을 맞출 수 있다.트랙 스탠드를 수행하는 동안, 라이더는 앞바퀴를 한쪽으로 또는 다른 쪽으로 조정한 다음 앞뒤로 약간 이동하여 필요에 따라 앞쪽 접점 패치를 좌우로 이동시킴으로써 두 개의 접점 패치 사이의 선을 질량의 결합 중심 아래 유지할 수 있다.전진 동작은 페달을 밟기만 하면 발생할 수 있다.후진 동작은 고정 기어 자전거에서도 같은 방식으로 발생할 수 있다.그렇지 않으면 운전자가 적절한 포장도로 경사면을 이용하거나 브레이크가 일시적으로 체결된 상태에서 상체를 뒤로 젖힐 수 있다.^[32]

자전거 핸들이 잠기면 주행 중 균형을 잡는 것이 사실상 불가능해진다.반면 회전하는 자전거 바퀴의 자이로스코프 효과가 역회전 바퀴를 추가해 취소돼도 주행 중 균형을 잡기 쉽다.^[5][6]자전거가 잠금 조향장치를 사용하거나 사용하지 않고 균형을 이룰 수 있는 또 다른 방법은, 체조 선수가 고르지 않은 평행봉에서 똑바로 내려가는 것에서부터 위로 스윙을 시작할 수 있는 방법, 다리를 펌핑하여 정지 상태에서 스윙을 시작할 수 있는 방법, 또는 이중 역진자를 제어할 수 있는 방법과 유사한 토크를 자전거와 라이더 사이에 적용하는 것이다.팔꿈치에만 작동기를 부착한다.^[33]

전진 속도

승차자는 앞바퀴를 돌리기 위해 핸들 바에 토크를 가하여 기울기를 제어하고 균형을 유지한다.고속에서는 작은 조향 각도가 지면에 닿는 지점을 횡방향으로 빠르게 이동하며, 저속에서는 동일한 시간 내에 동일한 결과를 얻기 위해 더 큰 조향 각도가 필요하다.이 때문에 고속에서는 보통 균형을 유지하기가 더 쉽다.^[34]자기 안정성은 일반적으로 특정 임계값을 초과하는 속도에서 발생하기 때문에, 더 빨리 가는 것은 자전거 자체의 안정성에 기여할 가능성을 증가시킨다.

질량 위치의 중심

자전거와 라이더가 결합된 질량의 중심을 앞으로(앞바퀴에서 앞바퀴로 더 좁게) 더 멀수록 균형을 유지하기 위해 앞바퀴가 횡방향으로 덜 움직여야 한다.^[35]반대로 질량 중심이 더 먼 후방(뒷바퀴에 클로저)에 위치할수록 균형을 되찾기 위해서는 앞바퀴 측면 운동이나 자전거 전진 운동이 더 많이 필요하다.이는 롱휠베이스 리컴백, 헬퍼, 휠리 바이크에서 두드러질 수 있다.^[36]무거운 기어를 뒷바퀴 위나 뒤까지 운반하는 투어링 바이크에도 도전장이 될 수 있다.^[37]뒷바퀴 위의 질량은 앞바퀴 위의 질량보다 낮을 경우 더 쉽게 제어할 수 있다.^[11]

자전거는 또한 반전된 진자의 한 예다.빗자루가 연필보다 손안에서 더 쉽게 균형을 잡듯이, 키 큰 자전거(질량 중심이 높은 자전거)는 키 큰 자전거의 기울기 속도(넘어지기 시작하면 기울기 각도가 높아지는 속도)가 느리기 때문에 낮은 자전거보다 자전거를 탈 때 균형을 잡기가 더 쉽다.^[38]그러나, 자전거를 타는 사람은 정지해 있을 때 자전거와 정반대의 인상을 가질 수 있다.예를 들어, 상층부 자전거는 키가 크지만 질량이 낮은 자전거보다, 교통체증에서 멈추었을 때 똑바로 서 있기 위해 더 많은 노력을 필요로 할 수 있다.수직 2등급 레버의 예다.레버 끝에 있는 작은 힘, 자전거 상단에 있는 좌석 또는 핸들 바는 질량이 타이어가 지면에 닿는 풀크럼에 가까우면 더 쉽게 큰 질량을 이동시킨다.자전거 여행을 하는 사람들은 자전거에 짐을 낮게 싣고 다니도록 권하고, 패니어는 앞뒤 선반의 양쪽에 늘어져 있는 것도 이 때문이다.^[39]

트레일

자전거가 얼마나 쉽게 주행할 수 있고 어려운지에 영향을 미치는 요인은 앞바퀴 접지 접점이 조향 축 접지 접점 뒤쪽으로 향하는 거리인 트레일이다.조향축은 전체 조향 메커니즘(포크, 핸들 바, 프론트 휠 등)이 선회하는 축이다.전통적인 자전거 설계에서, 조향 축이 수직에서 뒤로 기울어진 상태에서, 양방향 트레일은 전방 속도에 관계 없이 앞 바퀴를 기울인 방향으로 조향하는 경향이 있다.^[28]이것은 정지해 있는 자전거를 한쪽으로 밀어서 시뮬레이션할 수 있다.앞바퀴도 대개 저쪽으로 방향을 틀 것이다.기울어진 상태에서 중력은 이러한 힘을 제공한다.그러나 움직이는 자전거의 역학관계는 더 복잡하며, 다른 요소들은 이러한 효과의 원인이 되거나 그 영향을 감소시킬 수 있다.^[1]

트레일은 헤드 앵글, 포크 오프셋 또는 레이크, 휠 크기의 함수다.이들의 관계는 다음과 같은 공식으로 설명할 수 있다.^[40]

${\displaystyle {\text{Trail}}={\frac {(R_{w})\cos(A_{h}-O_{f}}}}{\sin(A_{h}}}}}}}}}}}}}}$

여기서 $R{\displaystyle {}_{}}$ ${\displaystyle w_{}}$ ${\$는 휠 반지름이고, $A{\displaystyle {}_{}}$ ${\displaystyle h_{}}$ ${\$는 수평에서 시계 방향으로 측정된 헤드 각도이며, ${\displaystyle {Of}_{}}$ ${\$는 포크$$ 오프셋 또는 레이크다.트레일은 휠 크기를 증가시키거나, 헤드 각도를 감소시키거나, 포크 레이크를 감소시킴으로써 증가할 수 있다.

기존 자전거의 트레일이 많을수록 안정감을 느끼지만,^[41] 너무 많은 트레일이 자전거를 조종하는 것을 어렵게 할 수 있다.음의 자국이 있는 자전거(조향축이 지면과 교차하는 곳 앞에 접점이 있는 자전거)는 주행성이 여전히 높으면서도 매우 불안정한 것으로 보고되고 있다.보통, 도로 경주용 자전거는 자전거 관광보다는 오솔길이 더 많지만 산악용 자전거보다는 적다.산악자전거는 자전거보다 수직성이 낮은 헤드 각도로 설계되어 트레일이 넓어 하강을 위한 안정성이 향상되었다.투어링 바이크는 작은 오솔길과 함께 제작되어 탑승자가 짐으로 짓눌린 자전거를 제어할 수 있다.그 결과, 짐을 싣지 않은 관광자전거는 불안정을 느낄 수 있다.자전거에서, 포크 레이크는 종종 조향 축의 앞 포크 블레이드의 곡선으로, 오솔길을 줄이기 위해 사용된다.^[42]파이톤 로우레이커와 같이 마이너스 트레일이 있는 자전거가 존재하며 탈 수 있으며, 마이너스 트레일이 있는 실험용 자전거는 스스로 안정성이 있는 것으로 나타났다.^[1]

오토바이에서 갈퀴는 대신 머리 각도를 가리키며, 삼나무에 의해 만들어진 오프셋은 오솔길을 줄이기 위해 사용된다.^[43]

위트와 윌슨의^[28] 소규모 조사는 다음과 같은 사실을 발견했다.

• 헤드 앵글이 72~73°이고 트레일이 43~60mm인 투어링 자전거
• 헤드 앵글이 73~74°이고 트레일이 28~45mm인 경주용 자전거
• 자전거의 헤드 각도가 75°이고 트레일이 23.5mm~37mm인 트랙.

그러나 이 범위들은 단단하고 빠르지 않다.예를 들어, LeMond Racing Cycles는 오프셋 또는 레이크가 45mm이고 휠 크기가 같은 포크 모두를 제공한다.

• 2006년 테데 드 코스(Tete de Course)는 도로 경주를 위해 설계되었으며, 프레임 크기에 따라 헤드 각도가 71˚~74°이며, 따라서 트레일이 51.5mm~69mm까지 다양하다.
• 2007년식 필모어(Filmore) 트랙용으로 설계되었으며, 프레임 크기에 따라 헤드 각도가 72° ~ 74°이며, 따라서 51.5mm ~ 61mm의 트레일이 달라진다.

특정 자전거가 가지고 있는 산책로의 양은 여러 가지 이유로 시간에 따라 달라질 수 있다.프론트 서스펜션, 특히 텔레스코픽 포크가 장착된 자전거에서 예를 들어 제동이 많이 걸려 프론트 서스펜션을 압축하면 스티어링 축 각도가 침강되고 트레일이 감소할 수 있다.트레일은 또한 기울어진 각도와 조향 각도에 따라 달라지는데, 보통 자전거가 직립하고 직진할 때 최대치에서 감소한다.^[45]트레일은 충분히 큰 기울기와 조향 각도로 0까지 감소할 수 있으며, 이것은 자전거가 얼마나 안정감을 느끼는지를 바꿀 수 있다.^[11]마지막으로, 앞 타이어의 프로필도 자전거가 기울어지고 조향될 때 트레일이 어떻게 변화하는지에 영향을 미칠 수 있다.

기계적 트레일, 정상 트레일 또는 참 트레일로 불리는 트레일과 유사한 측정은 ^[46]조향 축에서 전면 휠 접촉 패치의 중심까지의 수직 거리다.

휠베이스

자전거의 방향 안정성에 영향을 미치는 요인은 앞바퀴와 뒷바퀴의 접지 접점 사이의 수평 거리인 휠베이스다.일정한 전륜 변위의 경우, 어떤 교란으로 인해 원래 경로로부터의 결과 경로의 각도는 휠베이스에 반비례한다.^[9]또한 주어진 조향 각도와 기울어진 각도에 대한 곡률 반경은 휠베이스에 비례한다.^[9]마지막으로, 자전거가 기울고 조향될 때 휠베이스가 증가한다.극단적으로 기울어진 각도가 90°이고, 자전거가 그 기울어진 방향으로 조향될 때, 휠베이스는 앞바퀴와 뒷바퀴의 반지름에 의해 증가한다.^[11]

스티어링 메커니즘 매스 분배

전통적인 자전거 설계의 자기 안정성에 기여할 수 있는 또 다른 요인은 앞바퀴, 포크, 핸들바를 포함하는 조향 메커니즘에서의 질량의 분포다.조향 메커니즘을 위한 질량의 중심이 조향 축 앞에 있는 경우, 중력의 당김으로 인해 앞바퀴가 기울어진 방향으로 조향되기도 한다.정지해 있는 자전거를 한쪽으로 기울이면 이를 알 수 있다.또한 전면 바퀴는 일반적으로 지면과의 상호작용과는 무관하게 그쪽으로 조향한다.^[47]질량 중심의 전후 위치 및 질량 중심 고도와 같은 추가 매개변수도 자전거의 동적 거동에 기여한다.^[28][47]

자이로스코프 효과

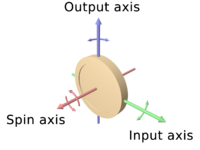
대부분의 자전거 디자인에서 자이로스코프 효과의 역할은 앞바퀴를 기울어지게 하는 것이다.이 현상을 '전진'이라고 하며, 물체가 전진하는 속도는 그 회전 속도에 반비례한다.앞바퀴가 천천히 돌수록 자전거가 기울면 빨리 지나가고 그 반대도 마찬가지다.^[48]뒷바퀴는 앞바퀴가 지면에 있는 타이어의 마찰로 인해 전륜처럼 전처리되는 것을 막아 전혀 회전하지 않은 것처럼 계속 기울어진다.따라서 자이로스코프 힘은 팁을 주는 데 어떤 저항도 제공하지 않는다.^[49]

낮은 전진 속도에서 앞바퀴의 전진은 너무 빨라서 제어되지 않는 자전거의 오버스티어 경향에 기여하고 반대로 기울기 시작하고 결국 진동하여 넘어진다.높은 전방 속도에서 전열은 보통 너무 느려서 제어되지 않는 자전거의 언더스티어 경향에 기여하고 결국 직립 위치에 도달하지 못하고 넘어진다.^[11]이 불안정성은 초의 순서로 매우 느리고 대부분의 기수들이 대응하기에 쉽다.따라서, 고속 자전거는 실제로 스스로 안정적이지 못하고 조종하지 않으면 넘어질 수 있음에도 불구하고 안정감을 느낄 수 있다.

자이로스코프 효과의 또 다른 기여는 역스티어링 중 앞바퀴에 의해 발생하는 롤 모멘트다.예를 들어, 좌회전 조향은 우측으로 순간의 원인이 된다.아웃트랙팅 프론트 휠에서 발생하는 순간과 비교하면 순간은 작지만, 주행자가 핸들 바에 토크를 가하는 순간 시작되기 때문에 오토바이 레이싱에 도움이 될 수 있다.^[9]자세한 내용은 아래 섹션 역스티어링 및 역스티어링 문서를 참조하십시오.

자기안정성

앞 절에서 언급된 두 가지 불안정한 제도 사이에 균형(트레일, 질량 분포, 자이로스코프 효과 등)에 기여하는 위에서 설명한 모든 요인의 영향을 받아 이러한 효과가 제어되지 않은 자전거를 직립으로 조종하는 특정 자전거 설계의 전방 속도 범위가 있을 수 있다.^[2]자이로스코프 효과나 양성 추적은 물론 핸즈프리 제어를 강화할 수 있지만 스스로 충분하거나 자기 안정성에 필요하다는 사실이 입증됐다.^[1]

그러나, 자기 안정성이 없더라도 자전거는 바퀴 위에 자전거를 고정시키기 위해 조종함으로써 탈 수 있다.^[6]위에서 언급한 효과는 헤드셋 마찰 및 뻣뻣한 제어 케이블과 같은 추가 요인에 의해 압도될 수 있다는 점에 유의하십시오.^[28]이 동영상은 라이더 없는 자전거가 자기 안정감을 보여주는 것을 보여준다.

종가속도

종방향 가속도는 횡방향 역학에 크고 복잡한 영향을 미치는 것으로 나타났다.한 연구에서 양의 가속은 자기 안정을 없애고, 음의 가속(감속)은 자기 안정의 속도를 변화시킨다.^[7]

도는

자전거가 회전하기 위해서, 즉, 전방 이동 방향을 바꾸려면, 앞 바퀴는 다른 전륜 조향 차량과 마찬가지로 원하는 방향으로 대략적으로 조준해야 한다.그런 다음 휠과 지면 사이의 마찰은 선회력과 캠버 추력의 조합으로 직선 전방에서 코스를 변경하는 데 필요한 구심 가속도를 발생시킨다.직립(기울리지 않는) 자전거의 회전 반경은 작은 조향 각도에 대해 대략 다음과 같이 추정할 수 있다.

${\displaystyle r={\frac {w}{\properties \cos \left(\phi \오른쪽)}}}$

여기서 $r{\displaystyle }$ $displaystyle$ $r$$\,\!}$은(는) 대략적인 반지름이고 $w{\displaystyle }$ $displaystyle$ w$\,\}$은(는)^[9] 휠베이스, $\Delta {\displaystyle }$ ${\displaystyle \{\backslash }$$displaystyle \pi$$$$\,\}$은(는${\displaystyle )}$ 조향 축의 캐스터 각이다.

기울어짐

그러나 다른 바퀴 달린 차량과 달리 자전거도 회전 중에 기울어져야 관련 힘(중력, 관성, 마찰력, 지반 지지력)의 균형을 맞출 수 있다.희박, ,의 각도는 원형의 운동 법칙을 이용하여 쉽게 계산할 수 있다.

${\displaystyle \theta =\arctan \leftder\frac {v^{2}}:{gr}\오른쪽)}$

여기서 v는 전방 속도, r은 턴의 반지름, g는 중력의 가속이다.^[48]이것은 이상화된 경우에 해당된다.동일한 전방 속도와 회전 반지름에서 현대적인 타이어의 폭을 보상하기 위해 오토바이에 기울어진 각도를 약간 증가시켜야 할 수 있다.^[45]

그러나 이 단순한 2차원 모델, 본질적으로 턴테이블의 반전된 진자는 정상상태의 턴이 불안정하다고 예측한다는 것도 알 수 있다.평형 기울기 각도에서 자전거를 약간 아래쪽으로 이동시키면 중력의 토크가 증가하고 원심력이 감소하며 변위가 증폭된다.실제 자전거에서 관찰되는 자기 안정성을 포착하기 위해서는 바퀴가 방향을 잡고 경로를 조정하며 무게의 토크를 상쇄할 수 있는 보다 정교한 모델이 필요하다.

예를 들어 10m/s(36km/h, 22mph)에서 10m(33ft) 반경의 정상 상태 선회를 하는 자전거는 45.6°의 각도에 있어야 한다.기수는 원하면 몸통이나 자전거를 좀 더 직립하게 유지하기 위해 자전거에 대해 기울일 수 있다.중요한 각도는 수평면과 타이어 접점에 의해 정의된 평면 사이의 각도 및 자전거와 승차자의 질량 중심 위치다.

이 자전거의 기울기는 기울어진 각도의 코사인(cosine)에 비례하여 턴의 실제 반지름을 감소시킨다.결과 반경은 대략 다음과 같이 근사할 수 있다(정확한 값의 2% 이내).

${\displaystyle r={\frac {w\cos \left(\theta \right)}{\reft \cos \left(\phi \right)}{\reft;}}}$

여기서 r은 대략적인 반지름, w는 휠베이스, w은 기울어진 각도, Δ는 조향각, φ은 조향축의 캐스터각이다.^[9]자전거가 기울면 타이어의 접촉 패치가 옆으로 더 멀리 이동하여 마모를 일으킨다.오토바이 타이어의 양쪽 가장자리에서 차례대로 기댄 채 마모되지 않은 부분을 치킨 스트립이라고 부르기도 한다.

타이어의 유한 폭은 위에서 설명한 이상적인 기울기 각도에서 후면 프레임의 실제 기울기 각도를 변경한다.프레임과 수직 사이의 실제 기울기 각도는 타이어 너비에 따라 증가해야 하며 질량 높이의 중심에 따라 감소해야 한다.살찐 타이어와 질량 중심이 낮은 자전거는 스키니 타이어 또는 질량 중심이 더 높은 자전거보다 더 많이 기울어져야 같은 속도로 같은 회전을 협상할 수 있다.^[9]

타이어 두께 2t으로 인한 린 각도의 증가는 다음과 같이 계산할 수 있다.

${\displaystyle \arcsin \left(t{\frac {\sin(\phi )}{h-t}\오른쪽)}$

여기서 φ은 이상적인 기울어진 각도, h는 질량 중심의 높이다.^[9]예를 들어, 12인치 폭의 후면 타이어가 있는 오토바이는 t = 6인치일 것이다.자전거와 질량의 결합형 라이더 중심이 26인치의 높이에 있는 경우 25° 기울기를 7.28° 증가시켜야 한다.거의 30%의 증가타이어 폭이 6인치밖에 되지 않을 경우 기울어진 각도 상승은 3.16°에 불과하며, 절반도 안 된다.

중력과 지반 반응력에 의해 창조된 부부가 자전거가 아예 회전하기 위해 필요한 것으로 나타났다.스프링이 달린 아웃리거가 달린 맞춤 제작 자전거에서 자전거와 라이더가 직선 주행 시 기울어진 각도를 가정할 수 있도록 이 커플을 정확히 취소한다.바퀴가 직진 경로에서 벗어나자마자 자전거와 라이더가 반대 방향으로 기울기 시작하는데, 이를 바로잡을 수 있는 유일한 방법은 직진 경로로 다시 방향을 잡는 것이다.^[50][51]

역스티어링

턴을 시작하고 그 턴의 방향으로 필요한 기울기를 시작하기 위해, 자전거는 잠시 반대 방향으로 방향을 돌려야 한다.이것을 흔히 역스티어링이라고 한다.이제 앞바퀴가 움직임의 방향에 대해 유한 각도에 있는 상태에서, 타이어의 접점에서 횡력이 발생한다.이 힘은 자전거의 세로(롤) 축을 중심으로 토크를 생성하며, 이 토크는 자전거가 처음 조향된 방향에서 벗어나 원하는 회전 방향으로 기울게 한다.자전거를 기울이는 데 필요한 힘을 만들기 위한 기회적 측면 바람과 같은 외부 영향이 없는 경우, 빠른 회전을 시작하기 위해 역스티어링이 필요하다.^[48]

초기 조향 토크와 조향 각도가 모두 원하는 방향의 반대편에 있지만, 이는 정상 상태 선회를 유지하는 경우가 아닐 수 있다.지속 조향 각도는 대개 턴과 같은 방향에 있지만, 특히 고속에서 턴의 방향과 반대편에 있을 수 있다.^[52]조향 각도를 유지하는 데 필요한 지속 조향 토크는 보통 회전 방향과 반대편에 있다.^[53]특정 턴에서 특정 자전거의 지속 조향 각도와 지속 조향 토크 모두의 실제 크기와 방향은 전방 속도, 자전거 기하학, 타이어 특성 및 결합된 자전거와 승차자 질량 분포에 따라 달라진다.^[23]한 바퀴씩 돌아가면 적당한 기울기 각도로만 반지름을 변경할 수 있으며, 이는 턴 밖으로 추가 역스티어링을 통해 기울기를 증가시키고 반지름을 감소시킨 다음 턴으로 들어가 린을 감소시키고 반지름을 증가시키는 방식으로 이루어질 수 있다.턴을 벗어나려면 자전거가 다시 역방향 조향해야 하고, 반경을 줄이기 위해 순간적으로 턴으로 더 많이 조향해야 하며, 따라서 관성력이 증가하여 기울어짐의 각도가 감소한다.^[54]

정상 상태 회전

턴이 설정되면 일정한 전방 속도에서 일정한 반경을 유지하기 위해 조향 메커니즘에 적용해야 하는 토크는 자전거의 전방 속도와 기하학 및 질량 분포에 따라 달라진다.^[11][23]아래 아이겐값 섹션에 설명되어 있고 뒤집기 속도라고도 불리는 캡사이즈 속도 이하의 속도에서, 자전거의 자기 안정성은 회전 반대 방향으로 토크를 적용하지 않는 한, 자전거가 턴으로 방향을 틀고 턴을 빠져나가는 경향을 야기할 것이다.캡사이즈 속도를 초과하는 속도에서, 캡사이즈 불안정성은 회전 방향에서 토크를 가하지 않는 한, 턴을 벗어나게 하여 린을 증가시키는 경향이 있다.캡사이즈 속도에서는 정상 상태 회전을 유지하기 위해 입력 조향 토크가 필요하지 않다.

조향각

몇 가지 효과는 전방 어셈블리가 조향 축을 중심으로 회전하는 각도인 조향 각도에 영향을 미치며, 일정한 상태 회전을 유지하는 데 필요하다.이 중 일부는 싱글 트랙 차량에만 있는 것이 특징인 반면, 다른 일부는 자동차에 의해서도 경험된다.이 중 일부는 이 글의 다른 곳에 언급될 수 있으며, 반드시 중요도 순서는 아니지만 여기서 반복되어 한 곳에서 발견될 수 있다.

첫째, 전면 어셈블리가 회전하는 도로 평면에 투영되는 각도는 조향 각도와 조향 축 각도의 기능이다.

${\displaystyle \Delta =\delta \cos \left(\phi \오른쪽)}$

여기서 $\Delta {\displaystyle \mathrm{}}$ $displaystyle \Delta \,\!}$은(는) 키네마틱 조향각, $\Delta {\displaystyle }$ $displaystyle$$\delta \,\}$은${\displaystyle (}$^[9]는) 조향축의 캐스터각이다.

둘째, 자전거의 기울기는 기울어진 각도의 코사인(cosine)에 비례하여 턴의 실제 반지름을 감소시킨다.결과 반경은 대략 다음과 같이 근사할 수 있다(정확한 값의 2% 이내).

${\displaystyle r={\frac {w\cos \left(\theta \right)}{\reft \cos \left(\phi \right)}{\reft;}}}$

여기서 $r{\displaystyle }$ $displaystyle$ $r$$\,\!}$은(는) 대략적인 반지름이고 w $displaystyle$ w$\,\!}$은(^[9]는) 휠베이스$$, {${\displaystyle }${\$displaystyle$$\theta \,\}$은(는) 기울기 각도, $\Delta {\displaystyle }$${\displaystyle }$$displaystyle \phi \,\!}$은 스티어링 축의 캐스터 각이다$$.

셋째, 전면과 후면 타이어의 중량 분포, 타이어 특성 등으로 슬립 각도가 다를 수 있기 때문에 자전거는 언더스티어 또는 오버스티어를 경험할 수 있다.언더스티어링 시 조향 각도가 더 커야 하며, 오버스티어링 시 조향 각도가 주어진 회전 반경을 유지하는 것과 같을 경우 조향 각도가 이보다 작아야 한다.^[9]일부 저자들은 역방향 조향이라는 용어를 사용하여 일부 조건에서 턴의 반대 방향(음극 조향 각도)으로 조향하여 상당한 뒷바퀴 미끄러짐에 대응하여 제어력을 유지할 필요성을 언급하기도 한다.^[9]

넷째, 캠버 추력은 미끄러짐 각도로 인한 선회력과 함께 자전거가 직선 경로에서 이탈하도록 하는 데 필요한 구심력에 기여하며, 가장 큰 기여자가 될 수 있다.^[45]캠버 추력은 자전거가 자동차와 반지름은 같지만 조향 각도는 더 작은 회전을 협상하는 능력에 기여한다.^[45]자전거가 조향되고 같은 방향으로 기울어지면 앞 타이어의 캠버 각도가 후면보다 커지므로 더 많은 캠버 추력을 발생시킬 수 있고, 그 외 모든 것이 동일하다.^[9]

손을 놨어.

역스티어링은 보통 핸들에 직접 토크를 가함으로써 시작되지만, 자전거와 같은 가벼운 차량에서는 승차자의 체중을 이동시킴으로써도 가능하다.자전거를 탄 사람이 자전거에 비해 오른쪽으로 기울면 자전거는 각운동량을 보존하기 위해 왼쪽으로 기울어지며 질량의 결합 중심은 거의 같은 수직면에 머물러 있다.일부 저자에 의해 카운터 레인으로 불리는 이 자전거의 좌측 방향 기울기는 핸들 바에 직접 토크를 가함으로써 운전자가 좌측으로 역방향 조향한 것처럼 우측 방향 선회를 시작하게 할 것이다.^[45][48]이 기법은 헤드셋 마찰 및 뻣뻣한 제어 케이블과 같은 추가 요인에 의해 복잡해질 수 있다.

질량의 결합 중심은 운전자가 자전거에 비해 오른쪽으로 기울면 왼쪽으로 약간 이동하고 자전거는 응답으로 왼쪽으로 기울면 왼쪽으로 기울어진다.그 작용은 우주에서 타이어가 오른쪽으로 움직이게 하겠지만, 이것은 타이어와 지면 사이의 마찰에 의해 방지되어 질량의 결합 중심을 왼쪽으로 밀어낸다.그러나, 대부분의 사람들이 이 방법만으로 자전거를 균형잡기에 어려움을 겪고 있다는 것을 증명하듯이, 이것은 작은 효과다.

자이로스코프 효과

균형에 관한 섹션에서 언급한 바와 같이, 앞바퀴를 돌리는 한 가지 효과는 자이로스코프 프리세션에 의해 발생하는 롤 모멘트다.이 모멘트의 크기는 앞바퀴의 관성 모멘트, 그 회전율(전방 운동), 승차자가 핸들 바에 토크를 가해 앞바퀴를 돌리는 속도, 그리고 조향축과 수직 사이의 각도의 코사인 비율에 비례한다.^[9]

관성 모멘트가 0.6kg·m인² 앞바퀴가 22m/s(50mph)로 움직이는 표본 이륜자동차의 경우 앞바퀴를 0.5N·m로 1도 돌리면 3.5N·m의 롤 모멘트가 발생한다.이에 비해 앞 타이어가 오토바이 아래에서 빠져나올 때 전방 타이어의 횡력은 최대 50N에 이른다.질량 중심의 0.6m(2ft) 높이에 작용하는 이것은 30 N·m의 롤 모멘트를 생성한다.

자이로스코프 힘의 모멘트는 이 중 12%에 불과하지만, 휠 아웃트랙처럼 더 느리게 쌓이는 대신, 승차자가 토크를 가하는 순간 동작하기 시작하므로 중요한 역할을 할 수 있다.이것은 특히 오토바이 경주에서 도움이 될 수 있다.

이륜 스티어링

저속 주행 시 회전 반경이 더 촘촘해지는 등 이론적 이점 때문에 이륜 조향으로 오토바이를 건설하려는 시도가 있었다.호주의 Ian Drysdale에 의해 작동되는 한 프로토타입은 "매우 잘 작동한다"^[55][56]고 보고되었다.설계의 문제에는 후륜의 능동적인 제어를 제공할 것인지, 후륜이 자유롭게 휘도록 할 것인지 등이 포함된다.능동 제어의 경우, 제어 알고리즘은 앞바퀴의 반대 방향이나 방향, 시기, 그리고 얼마의 조향 사이에서 결정할 필요가 있다.2륜 조향 장치인 사이드 바이크는 운전자가 양쪽 바퀴의 조향을 직접 제어할 수 있게 해준다.또 다른 하나인 스윙 바이크는 핸들 바에 의해 조종될 수 있도록 좌석 앞에 두 번째 조향 축을 두었다.

밀턴 W. 레이먼드는 "X-2"라고 불리는 길고 낮은 2륜 조향 자전거를 만들었는데, 두 바퀴를 독립적으로 제어할 수 있는 다양한 조향 메커니즘이 적용되었다.조향 동작에는 두 바퀴가 함께 움직여 타이어 접점을 질량 중심 아래에서 조향하는 "균형"과 질량 중심과 비교하여 타이어 접점의 횡방향 위치를 실질적으로 변경하지 않고 휠이 반대 방향으로 조향하여 자전거를 조향하는 "진정한 원"이 포함되었다.X-2는 또한 앞바퀴가 도로 중심선 근처에 있고 뒷바퀴가 연석 근처에 있는 등, 바퀴가 평행하지만 프레임에 맞지 않는 상태에서 "크러브웨이즈"를 할 수 있었다.'밸런스' 조향은 휠베이스가 길고 질량의 중심이 낮음에도 불구하고 균형을 쉽게 잡을 수 있었지만, 자기 밸런싱("손 없음") 구성은 발견되지 않았다.스티어링이 타이어 패치와 질량 중앙의 정렬 오류에 대해 보정되지 않기 때문에 예상대로 참 원은 근본적으로 균형을 잡을 수 없었다.약 45°까지 시험한 각도에서 크랩을 이용한 사이클은 제동 중에도 넘어지는 경향을 보이지 않았다.^{[citation needed]}X-2는 Whitt와 Wilson의 자전거 과학 2번째 판에서 통과하는데 언급된다.^[28]

후륜 스티어링

이론적 이점, 특히 단순화된 전륜 구동 메커니즘 때문에 승차 가능한 후륜 조향 자전거를 제작하려는 시도가 있었다.벤딕스 사는 후륜 조향 자전거를 만들었고, 미국 교통부는 후륜 조향 오토바이의 건설을 위탁했는데, 이 둘 다 경계가 불가능한 것으로 판명되었다.일리노이주 앨튼에 위치한 레인보우 트레이너사는 "후방 조향 자전거인 리어 조향 자전거 I"를 성공적으로 탈 수 있는 첫 번째 사람에게 미화 5,000달러를 제공했다.^[57]누군가가 후륜 조향 자전거를 성공적으로 탄 문서화된 예는 매사추세츠 공과대학교의 L. H. Laiterman의 것으로, 특별히 설계된 리컴백 자전거를 탄 것이다.^[28]난이도는 후륜을 오른쪽으로 돌림으로써 달성된 좌회전이 처음에는 질량의 중심을 오른쪽으로 옮기고, 반대로 질량의 중심을 오른쪽으로 움직인다는 것이다.이것은 환경에 의해 유도된 레인을 보상하는 일을 복잡하게 만든다.^[58]공통 기하학적 구조와 질량 분포가 있는 자전거에 대한 고유값을 검사하면 후진 주행 시 후륜 조향 장치가 본질적으로 불안정하다는 것을 알 수 있다.이것은 그들이 비판할 수 없다는 것을 의미하는 것이 아니라, 그들을 통제하려는 노력이 더 높다는 것을 의미한다.^[59]그러나 이러한 문제를 겪지 않는 다른 특수 목적 설계도들이 출판되었다.^[1][60]

센터 스티어링

고전적인 전륜 조향 장치가 있는 자전거와 엄격한 후륜 조향 장치가 있는 자전거의 극한 사이에는 중심 조향이라고 하며, 관절형 조향과 유사한 피벗 포인트가 있는 자전거 종류가 있다.이 개념의 초기 구현은 1870년대 초반에 페니파잉에 대한 보다 안전한 대안으로 홍보된 팬텀 자전거였다.^[61]이 설계는 간단한 전륜 구동 방식을 허용하며, 많은 사진에서 알 수 있듯이 현재 구현은 상당히 안정적이고 심지어 탈 수 있는 손이 없는 것으로 보인다.^[62][63]

이러한 설계는 대개 뒤로 젖혀지는 파이톤 로우레이서(Python Lowracer)와 같이 머리 각도가 매우 느슨하다(40°~65°).긍정적이거나 심지어 부정적이기도 하다.음의 트레일이 있는 자전거의 제작자는 직진 주행에서 자전거를 조종하면 좌석(따라서 탑승자)이 약간 상승하게 되고 이는 음의 트레일의 불안정한 효과를 상쇄한다고 말한다.^[64]

후진 스티어링

자전거는 조사와 시연을 위해 제작되었으며, 핸들을 왼쪽으로 돌리면 앞바퀴가 오른쪽으로 돌게 되고, 반대 방향으로 돌게 된다.이런 자전거는 탈 수 있지만 일반 자전거를 타는 사람들은 전혀 관리할 수 있다면 배우는 것이 매우 어렵다는 것이 밝혀졌다.^[65][66]

틸러 효과

틸러 효과는 조향축(헤드 튜브) 뒤로 멀리 뻗은 핸들 바가 보트 위의 틸러처럼 어떻게 작용하는지 설명하는 표현으로, 앞바퀴를 왼쪽으로 돌리기 위해 바를 오른쪽으로 움직인다는 점에서, 그 반대도 마찬가지다.이런 상황은 흔히 순양함 자전거, 어떤 낙후된 자전거, 그리고 어떤 오토바이에서 발견된다.^[67]간섭이나 팔 닿는 한계 때문에 조향 능력을 제한할 때는 골치 아플 수 있다.^[68]

타이어

타이어는 자전거 취급, 특히 오토바이에 ^[9][45]미치는 영향이 크지만 자전거에도 큰 영향을 미친다.^[7][69]타이어는 두 가지 뚜렷한 방식으로 자전거 역학에 영향을 미친다: 유한 왕관 반지름과 힘 생성.전면 타이어의 크라운 반경을 증가시키면 크기가 감소하거나 자체 안정성이 제거되는 것으로 나타났다.후면 타이어의 크라운 반경을 늘리면 반대 효과가 있지만, 그 정도는 덜하다.^[7]

타이어는 선회력과 캠버 추력의 조합을 통해 조향과 균형을 잡는 데 필요한 횡력을 발생시킨다.타이어 팽창 압력도 고속에서 오토바이 동작에 중요한 변수로 밝혀졌다.^[70]전면과 후면 타이어는 중량 분포, 타이어 특성 등으로 슬립 각도가 다를 수 있어 자전거는 언더스티어 또는 오버스티어를 경험할 수 있다.둘 중 앞바퀴가 뒷바퀴보다 더 많이 미끄러지는 언더스티어는 앞바퀴 조향이 균형을 유지하는 데 중요하기 때문에 더 위험하다.^[9]또한 실제 타이어는 스크럽 토크를 발생시킬 수 있는 노면과의 접촉 패치가 유한하기 때문에, 회전할 때 어느 한쪽이 미끄러지는 것을 경험할 수 있으며, 접촉 패치의 평면에 정상적인 축에 대한 토크를 생성할 수 있다.

타이어에 의해 생성된 하나의 토크는 접촉 패치 길이를 따라 횡방향 미끄럼의 비대칭에 의해 발생한다.이 사이드 슬립의 결과 힘은 공압 트레일로 묘사되는 거리인 접촉 패치의 기하학적 중심 뒤에서 발생하므로 타이어에 토크를 생성한다.사이드 슬립의 방향이 턴 바깥쪽을 향하기 때문에 타이어에 가해지는 힘은 턴의 중심을 향한다.따라서 이 토크는 턴 방향에서 벗어나 앞바퀴를 사이드 슬립 방향으로 돌리는 경향이 있고, 따라서 턴의 반경을 증가시키는 경향이 있다.

또 다른 토크는 접점 패치의 유한 폭과 타이어의 기울기에 의해 턴으로 생성된다.바퀴의 바깥쪽을 향한 접점 패치의 부분은 허브로부터 더 큰 반지름 때문에 나머지 접점보다 더 빠른 휠 허브와 관련하여 실제로 후방으로 이동하고 있다.같은 추리에 의해 내부는 더 천천히 후방으로 이동하고 있다.그래서 접점 패치의 외측과 내측 부분이 반대 방향으로 미끄러져 앞바퀴가 회전 방향으로 회전하는 경향이 있는 토크를 발생시켜 회전 반경을 감소시키는 경향이 있다.

이 두 개의 반대 방향 토크를 조합하면 앞 바퀴에 요 토크가 생성되며, 그 방향은 타이어의 사이드 슬립 각도, 타이어의 실제 경로와 타이어가 가리키는 방향 사이의 각도, 그리고 타이어의 캠버 각도(타이어가 수직에서 기울어가는 각도)의 기능이다.^[9]이 토크의 결과는 정상 상태 회전 시 위에서 설명한 강성 휠 모델에 의해 예측된 반전 속도의 억제인 경우가 많다.^[11]

하이사이드

하이사이더, 하이사이드 또는 하이사이드(high-side)는 주로 커브길에서 옆으로 미끄러진 후 주행 방향으로 향하지 않을 때 뒷바퀴가 트랙션을 얻어 발생하는 자전거 운동의 일종이다.^[9]이는 특히 구동렬과의 상호 작용으로 인해 급제동, 가속, 다양한 노면 또는 서스펜션 작동 시 발생할 수 있다.^[71]그것은 하나의 슬립-그 후 플립 또는 일련의 격렬한 진동 형태를 취할 수 있다.^[45]

기동성 및 핸들링

자전거의 기동성과 핸들링은 몇 가지 이유로 정량화하기가 어렵다.자전거의 기하학적 구조, 특히 조향 축 각도는 운동학적 분석을 복잡하게 만든다.^[2]많은 조건에서 자전거는 본질적으로 불안정하며 항상 승차자의 통제 하에 있어야 한다.마지막으로, 기수의 기술은 어떠한 기동에서도 자전거의 성능에 큰 영향을 미친다.^[9]자전거 설계는 기동성과 안정성 사이의 절충으로 구성되는 경향이 있다.

승차자 제어 입력

승차자가 할 수 있는 1차 제어 입력은 핸들 바를 통해 조향 장치에 직접 토크를 가하는 것이다.자전거 자체의 역동성 때문에 조향 기하학 및 자이로스코프 효과로 조향 각도에 대한 직접 위치 제어가 문제가 있는 것으로 밝혀졌다.^[8]

운전자가 할 수 있는 2차 제어 입력은 자전거에 비해 상반신을 기울이는 것이다.위에서 언급했듯이 라이더 린의 효과는 자전거의 질량에 반비례한다.오토바이와 같은 헤비 바이크의 경우 라이더 기울기는 대부분 한 바퀴씩 지상고 요구 사항을 변경하고, 도로의 시야를 개선하며, 자전거 시스템의 역동성을 매우 저주파 수동적으로 개선한다.^[8]오토바이 경주에서 몸통을 기대고, 몸을 움직이며, 자전거에 비해 회전 안쪽까지 무릎을 투영하는 것도 턴에 들어가 반올림을 용이하게 하는 공기역학적 요잉 모멘트를 유발할 수 있다.^[9]

자동차와의 차이

승차자의 부상과 차량 손상을 방지하기 위해 자전거를 똑바로 세워야 하는 필요성은 일반적으로 수행되는 기동성 시험의 유형을 제한하기도 한다.예를 들어, 자동차 애호가 출판물은 종종 스키드패드 결과를 공연하고 인용하지만, 오토바이 출판물은 그렇지 않다.회전을 위해 "설정"하고, 자전거를 적절한 각도로 기울여야 한다는 것은 승차자가 같은 속도로 일반 자동차에 필요한 것보다 더 멀리 앞을 보아야 한다는 것을 의미하며, 이러한 필요성은 속도에 비례하여 증가한다.^[8]

등급 체계

자전거, 특히 오토바이의 취급도를 평가하기 위한 몇 가지 계획이 고안되었다.^[9]

• 롤 인덱스는 스티어링 토크와 롤링 또는 린 각도 사이의 비율이다.
• 가속 지수는 조향 토크와 횡방향 또는 구심 가속도 사이의 비율이다.
• 조향 비율은 이상적인 타이어 행동에 기초한 이론적 회전 반경과 실제 회전 반경의 비율이다.^[9]프론트 휠 사이드 슬립이 리어 휠 사이드 슬립보다 큰 경우 1보다 작은 값은 언더스티어링, 1보다 큰 값은 중립 스티어링, 1보다 큰 값은 오버스티어링으로 설명된다.0보다 작은 값으로, 앞바퀴보다 훨씬 큰 뒷바퀴 사이드 슬립으로 인해 앞바퀴가 곡선 방향과 반대 방향으로 회전해야 하는 값을 역방향 조향으로 설명하였다.승차자는 중립적이거나 약간 오버스티어링을 선호하는 경향이 있다.^[9]자동차 운전자들은 언더스티어링을 선호하는 경향이 있다.
• 코흐 지수는 피크 조향 토크와 피크 린 레이트와 전방 속도 사이의 비율이다.^[72][73]대형 투어링 오토바이는 코흐 지수가 높은 편이고 스포츠 오토바이는 중형 코흐 지수를, 스쿠터는 코흐 지수가 낮은 편이다.^[9]무거운 오토바이보다 가벼운 스쿠터를 조작하는 것이 더 쉽다.

횡운동이론

비록 그것의 운동 방정식은 선형화될 수 있지만, 자전거는 비선형 시스템이다.해결해야 할 변수는 독립적 요소의 선형 합으로 쓸 수 없다. 즉, 변수의 행동은 설명자의 행동의 합으로 표현될 수 없다.^[2]일반적으로 비선형 시스템은 선형 시스템보다 해결이 어렵고 이해도가 훨씬 떨어진다.마찰과 굴곡이 무시되는 이상화된 경우 자전거는 보수적인 시스템이다.그러나 댐핑은 여전히 증명할 수 있다. 올바른 상황에서는 시간이 지남에 따라 측면 진동이 감소한다.직립과 직립을 달리는 자전거에 측면 충격으로 추가된 에너지(자율성 입증)는 진동이 사라지면서 손실이 아닌 전진 속도가 빨라진다.^[2]

자전거는 그 결과가 경로에 의존하기 때문에 비혼수 시스템이다.그것의 정확한 구성, 특히 위치를 알기 위해서는 부품의 구성뿐만 아니라 그들의 이력, 즉 시간이 지남에 따라 어떻게 움직였는지 알아야 한다.이것은 수학적 분석을 복잡하게 한다.^[48]마지막으로, 제어 이론의 언어에서, 자전거는 최소 위상 동작을 보이지 않는다.^[74]역방향 조향에 대한 위에서 설명한 바와 같이, 초기 조향 방식과 반대 방향으로 회전한다.

자유도

자전거의 자유도는 사용 중인 특정 모델에 따라 달라진다.키 동적 기능을 포착하는 가장 간단한 모델, 프랜시스 휘플는 맨 처음으로 방정식들이 개발된 후"휘플 모델"라고 불리는 it,[2]칼날 바퀴 전표 없이 평평한 매끄러운 표면을 뒹굴고,(구성 변수 필요한 완전히 찾거나 설명하기 위해 자유의 7도 네개의 엄격한 기관을 보유하고 있다.의하면4개 본체의 NTation):^[2]

1. x 뒷바퀴 접점 좌표
2. y 리어 휠 접점 좌표
3. 후면 프레임의 방향각(각각)
4. 뒷바퀴 회전각
5. 앞바퀴 회전각
6. 후면 프레임의 기울어진 각도(롤)
7. 리어 프레임과 프론트 엔드 사이의 스티어링 각도

라이더 이동, 서스펜션 이동, 타이어 컴플라이언스 또는 프레임 유연성과 같은 모델에 복잡성을 추가하면 자유도가 높아진다.후면 프레임은 기울기와 조향으로 피치를 하는 반면, 피치 각도는 양쪽 바퀴가 지면에 남아 있어야 하는 요건에 의해 완전히 구속되므로, 나머지 7개 변수로부터 기하학적으로 계산할 수 있다.자전거의 위치와 바퀴의 회전을 무시하면 처음 5도의 자유도 무시할 수 있고 자전거는 기울어진 각도와 조향각이라는 두 가지 변수만으로 설명할 수 있다.

운동 방정식

이상화된 자전거의 운동 방정식은 다음과 같이 구성된다.

• 단단한 뼈대,
• 단단한 포크,
• 칼날과 단단한 바퀴 두 개
• 모든 것이 무마찰 베어링과 연결되고 부드러운 수평 표면에서 마찰이나 미끄러짐 없이 굴러간다.
• 직립 및 직립, 불안정한 평형상태에서 또는 그 근처에서 작동

단일 4차 선형화된 일반 미분 방정식 또는 결합된 2차 미분 방정식,^[2] 희박 방정식으로 나타낼 수 있다.

${\displaystyle M_{\theta \theta }{\ddot {\theta _{r}}}+K_{\theta \theta }\theta _{r}+M_{\theta \psi }{\ddot {\psi }}+C_{\theta \psi }{\dot {\psi }}+K_{\theta \psi }\psi =M_{\theta }}$

그리고 조향 방정식

${\displaystyle M_{\psi \psi }{\ddot {\psi }}+C_{\psi \psi }{\dot {\psi }}+K_{\psi \psi }\psi +M_{\psi \theta }{\ddot {\theta _{r}}}+C_{\psi \theta }{\dot {\theta _{r}}}+K_{\psi \theta }\theta _{r}=M_{\psi }{\mbox{,}}}$

어디에

• ${\displaystyle {\theta }_{}}$ ${\displaystyle r_{}}$ ${\$는 후면 어셈블리의 기울어진 각도,
• ${\displaystyle \psi }$ ${\displaystyle \psi$}은$$(는) 후면 어셈블리에 상대적인 전면 어셈블리의 조향각이며
• ${\displaystyle M_{}}$ ${\$과 $M{\displaystyle {}_{}}$ ${\displaystyle {\psi }_{}}$ ${\$은(는) 후면 어셈블리와 조향 축에 각각 적용되는 모멘트(토크)이다$$.제어되지 않는 자전거의 분석은 둘 다 0으로 간주된다.

이것들은 다음과 같이 행렬 형태로 나타낼 수 있다.

${\ddot} +C\mathbf {\dot{q} +C\mathbf {q} +K\mathbf {q} =\mathbf {f}}}$

어디에

• ${\displaystyle M}$ ${\displaystyle M}$은 자전거의 질량과 기하학만 포함하는 대칭 질량 행렬이다.
• ${\displaystyle C}$ ${\displaystyle C}$은(는) 이상적인 자전거는 소산이 없더라도 소위 댐핑 매트릭스(daming matrix)로$$, 전진 속도 $v{\displaystyle }$ ${\displaystyle v}$을(를) 포함하고 비대칭이며,
• ${\displaystyle K}$ ${\displaystyle$ $K$$}$은 중력 $상수{\displaystyle }$ g ${\displaystyle g}$과 ${\displaystyle {v\mathrm{}}^{}}$ 2 ${\$$^{2}}$의 항을 포함하는 이른바 강성 행렬로, $g$ ${\$$displaystyle$ $g}$에서는 대칭이고 v ${\displaystyle 2^{}}$에서는 비대칭이다$.$
• ${\displaystyle \mathbf{q}}$ ${\$는) 희박각과 조향각의 벡터로서$$,
• ${\displaystyle \mathbf{f}}$ ${\$은(는) 위에서 언급한 순간인 외부 힘의 벡터다$$.

이 이상화·선형화 모델에는 기하학적 파라미터(휠베이스, 헤드 각도, 각 본체의 질량, 휠 반지름 등)가 많지만, 기울어진 각도, 기울어진 속도, 조향각, 조향률 등 4개의 유의미한 변수만 있다.이러한 방정식은 완전히 독립적으로 파생된 복수의 숫자 모델과 비교하여 검증되었다.^[2]

이 방정식은 자전거가 조향 토크 피드백에 대한 롤링 가속도, 롤링 속도 및 롤 변위를 나타내는 용어로 제어되는 지지대의 측면 위치를 가진 반전 진자와 같다는 것을 보여준다.롤 가속 항은 일반적으로 자기 안정화의 잘못된 기호의 것이며 주로 흔들리는 진동과 관련하여 중요할 것으로 예상할 수 있다.롤 속도 피드백은 정확한 부호이며, 자연적으로 자이로스코프하며, 속도에 비례하며, 앞바퀴의 기여도에 의해 지배된다.롤 변위 항은 가장 중요하며 주로 트레일, 조향 레이크 및 조향 축으로부터의 전면 프레임 매스 중앙의 오프셋에 의해 제어된다.모든 용어는 자전거 설계 매개변수와 때로는 속도의 복잡한 조합을 포함한다.벤치마크 자전거의 한계를 고려하고 타이어, 프레임 및 라이더 처리의 연장 ^[75]및 그 시사점을 포함한다.안정화 및 경로 추종 제어를 위한 최적 승차자 제어 장치도 논의된다.^[7]

아이겐값

특정 자전거 설계의 정상 모드와 자기 안정성을 분석하기 위해 선형화된 방정식에서 4개 상태 변수(경계각, 기울어짐 속도, 조향각, 조향 속도) 각각에 대해 1개씩 고유값을 계산할 수 있다.오른쪽 그림에서 특정 자전거 1대의 고유값은 0~10m/s(22mph)의 전방 속도에 대해 계산된다.모든 고유값(암청색으로 표시)의 실제 부분이 음수일 때 자전거는 스스로 안정화된다.고유값(청록색으로 표시)의 상상의 부분이 0이 아닐 때 자전거는 진동을 나타낸다.고유값은 원점에 대한 점 대칭이므로 전방 속도에서 자체 안정 영역을 가진 자전거 설계는 동일한 속도로 역진하는 자체 안정성이 없다.^[2]

자전거의 움직임이 질적으로 변화하는 우측의 플롯에서 확인할 수 있는 세 가지 전진 속도가 있다.^[2]

1. 이 예에서 약 1m/s(2.2mph)에서 진동이 시작되는 전방 속도는 특성 다항식의 반복된 루트가 있기 때문에 이중 루트 속도라고도 한다(4개의 고유값 중 2개는 정확히 동일한 값을 갖는다).이 속도 이하로, 자전거는 뒤집힌 진자가 하는 것처럼 그냥 넘어진다.
2. 이 예에서 약 5.3m/s(12mph)의 호프 분기점에서 직물 모드 고유값이 양에서 음으로 전환되는 진동이 증가하지 않는 전방 속도를 직물 속도라고 한다.이 속도 이하에서는 제어되지 않은 자전거가 넘어질 때까지 진동이 증가한다.이 속도 이상으로 진동은 결국 소멸된다.
3. 이 예에서 약 8m/s(18mph)의 피치 포크 분기에서 캡사이즈 모드 고유값이 음에서 양으로 전환되는 비수술적 기울기가 증가하는 전방 속도를 캡사이즈 속도라고 한다.이 속도 이상으로, 이 비 스케일링 기울기는 결국 제어되지 않은 자전거가 넘어지게 한다.

이 마지막 두 속도 사이에 둘 다 존재하는 경우, 특정 자전거 설계가 자체 안정화되는 전방 속도 범위가 있다.고유값이 여기에 표시된 자전거의 경우, 자체 안정화 범위는 5.3–8.0m/s(12–18mph)이다.보통 안정(매우 부정)인 네 번째 고유값은 자전거가 이동하는 방향으로 회전하는 경향이 있어 앞바퀴의 주물거동을 나타낸다.이 이상적인 모델은 위에서 설명한 흔들림이나 흔들림 및 후방 흔들림 불안정성을 나타내지 않는다는 점에 유의하십시오.그것들은 지면 또는 다른 자유도와의 타이어 상호작용을 통합한 모델에서 볼 수 있다.^[9]

실제 자전거를 이용한 실험은 지금까지 고유값에 의해 예측된 짜임모드를 확인했다.타이어 슬립과 프레임 플렉시블은 최대 6m/s의 속도 범위에서 자전거의 횡방향 역학에는 중요하지 않은 것으로 밝혀졌다.^[76]여기에 나타난 고유값을 계산하는 데 사용되는 이상적인 자전거 모델은 실제 타이어가 생성할 수 있는 토크를 일체 포함하지 않으며, 따라서 Wilson과 Cossalter가 제안한 바와 같이 포장도로와 타이어 상호작용은 고속에서 캡사이즈 모드가 불안정해지는 것을 막을 수 없다.

모드

자전거는 복잡한 메커니즘으로서 다양한 모드를 가지고 있다: 그들이 움직일 수 있는 근본적인 방법.이러한 모드는 자전거 매개변수와 전방 속도에 따라 안정적이거나 불안정할 수 있다.이런 맥락에서, "안정적"은 제어되지 않은 자전거가 전방 속도가 유지되는 한 넘어지지 않고 계속 앞으로 굴러가는 것을 의미한다.반대로, "불안정"은 제어되지 않는 자전거가 결국 전방 속도를 유지하더라도 넘어지게 된다는 것을 의미한다.모드는 안정성을 전환하는 속도와 자전거가 그러한 모드를 경험할 때 기울어짐과 조향의 상대적인 단계에 의해 구별될 수 있다.모든 자전거 모션은 가능한 다양한 모드의 조합으로 구성되며, 자전거가 경험할 수 있는 세 가지 주요 모드는 캡사이즈, 짜임, 흔들림이다.^[2]덜 알려진 모드는 후방 흔들림이며, 대개 안정적이다.^[9]

캡사이즈

캡사이즈는 자전거가 진동 없이 넘어지는 것을 묘사하는 데 사용되는 단어다.캡사이즈 동안 제어되지 않은 전면 휠은 보통 기울어진 방향으로 조향되지만, 매우 높은 기울기 각도에 도달할 때까지 증가되는 기울기를 멈출 만큼 충분히 조향되지 않으며, 이때 조향은 반대 방향으로 회전할 수 있다.만약 자전거가 빠르게 앞으로 나아간다면, 캡사이즈는 매우 천천히 일어날 수 있다.캡사이즈 불안정성은 너무 느리기 때문에, 초의 순서로, 기수가 제어하기 쉽고, 실제로 기수가 턴에 필요한 기울기를 개시하는 데 사용된다.^[9]

대부분의 자전거의 경우 기하학적 구조와 질량 분포에 따라 저속에서는 캡사이즈가 안정적이며, 속도가 증가함에 따라 더 이상 안정적이지 않을 때까지 안정성이 떨어진다.그러나 많은 자전거의 경우, 타이어와 포장도로와의 상호작용이 고속에서 캡사이즈가 불안정해지는 것을 방지하기에 충분하다.^[9][11]

짜다

위브(Web)는 좌측과 우측으로 기울어짐 사이의 느린(0–4 Hz) 진동을 묘사하는 데 사용되는 단어로서, 그 반대의 경우도 마찬가지다.전체 자전거는 조향 각도, 기울어진 각도(롤), 헤딩 각도(요우)의 큰 변화에 영향을 받는다.조향은 헤딩과 180° 위상 이탈, 기울임과 90° 위상 이탈이다.^[9]이 AVI 영화는 짜임새를 보여준다.

대부분의 자전거의 경우, 기하학이나 질량 분포에 따라 저속에서는 짜임이 불안정하며, 속도가 증가함에 따라 더 이상 불안정하지 않을 때까지 덜 뚜렷해진다.진폭은 감소할 수 있지만 주파수는 실제로 속도에 따라 증가한다.^[15]

흔들림 또는 흔들림

흔들림, 흔들림, 탱크 슬래퍼, 속도 흔들림, 죽음의 흔들림은 모두 주로 앞쪽 끝(앞바퀴, 포크, 핸들 바)의 빠른(4–10Hz) 진동을 설명하는 단어와 구절이다.또한 리어 프레임의 요잉도 포함되어 있어 너무 유연할 경우 흔들림이 발생할 수 있다.^[77]이러한 불안정성은 대부분 고속에서 발생하며 쇼핑 카트 바퀴, 비행기 착륙장치, 자동차 앞바퀴가 경험하는 것과 유사하다.^[9][11]속도나 위치, 핸들 바의 그립을 조절하여 흔들림이나 흔들림을 쉽게 교정할 수 있지만, 제어하지 않고 그대로 두면 치명적일 수 있다.^[78]

흔들림이나 흔들림은 포크 비대칭과 같은 다른 사소한 불규칙성이 ^[79]바퀴를 한쪽으로 가속시킬 때 시작된다.복원력은 불규칙의 진행과 함께 단계적으로 적용되며, 바퀴는 그 과정이 반복되는 반대쪽으로 돌아간다.스티어링에 댐핑이 불충분할 경우 시스템 고장이 발생할 때까지 진동이 증가한다.진동 주파수는 주행자가 주요 구성 요소인 전방 속도를 변경하여 자전거를 더 딱딱하거나 가볍게 만들거나 조향의 강성을 높임으로써 변경할 수 있다.^[16][28]

뒤 흔들림

후방 흔들림이라는 용어는 린 각도(롤)와 헤딩 각도(요우)가 거의 위상에 있고 조향 각도와 함께 180° 위상에 벗어나는 진동 모드를 설명하기 위해 사용된다.이 진동 속도는 약 6.5Hz로 보통이다.리어 워블은 습기가 많이 차서 자전거 속도가 증가함에 따라 빠르게 떨어진다.^[9]

설계기준

자전거의 설계 매개변수가 이러한 모드에 미치는 영향은 선형화된 운동 방정식의 고유값을 조사하여 조사할 수 있다.^[70]운동 방정식과 고유값에 대한 자세한 내용은 위의 운동 방정식에 대한 섹션을 참조하십시오.여기에 도출된 몇 가지 일반적인 결론이 설명되어 있다.

후면 프레임과 휠 스핀들의 횡방향 및 비틀림 강성은 흔들 모드 댐핑에 상당한 영향을 미친다.긴 휠베이스와 트레일과 평평한 스티어링 헤드 각도가 직물 모드 댐핑을 증가시키는 것으로 밝혀졌다.횡방향 왜곡은 가능한 한 낮게 프론트 포크 비틀림 축을 배치하여 방지할 수 있다.

코너링 짜임 경향은 리어 서스펜션의 댐핑 성능 저하에 의해 증폭된다.리어 타이어의 코너링, 캠버 뻣뻣함 및 이완 길이는 댐핑을 짜는 데 가장 큰 기여를 한다.전면 타이어의 동일한 매개변수는 효과가 적다.후방 하중은 코너링 짜임 경향도 증폭시킨다.그러나 적절한 강성과 댐핑을 가진 후면 부하 어셈블리는 직물 및 흔들림 진동을 감쇠하는 데 성공했다.

한 연구는 이론적으로 자전거가 회전하는 동안 도로의 굴절은 고속의 짜임모드나 그 중 하나의 주파수가 차량 속도와 다른 매개변수와 일치할 경우 저속에서의 흔들림모드를 자극할 수 있다는 것을 보여주었다.흔들림 모드의 흥분은 효과적인 조향 댐퍼에 의해 완화될 수 있으며 짜임 모드의 흥분은 무거운 라이더보다 가벼운 라이더에게 더 나쁘다.^[14]

러닝머신 및 롤러에 탑승

러닝머신 타는 것은 이론적으로 정지해 있는 포장도로를 타는 것과 동일하며, 물리적 테스트에서 이를 확인했다.^[80]트레드밀은 실내 자전거 훈련을 위해 특별히 개발되었다.^[81][82]롤러에 타는 것은 여전히 조사 중이다.^[83][84][85]

기타 가설

자전거와 오토바이는 4개의 주요 이동 부품(프레임, 포크, 2개의 바퀴)만 있으면 단순한 메커니즘으로 보일 수 있지만, 이러한 부품들은 분석이 복잡하게 되는 방식으로 배열되어 있다.^[28]바퀴의 자이로스코프 효과가 취소되어도 자전거를 탈 수 있다는 것은 관찰 가능한 사실이지만,^[5][6] 바퀴의 자이로스코프 효과가 자전거를 똑바로 세워두는 것이라는 가설은 인쇄물과 온라인에서 흔히 볼 수 있다.^[5][48]

인쇄 예:

• "사각형 모멘텀과 오토바이 역주행: 토론과 시연", A. J. Cox, Am. J. 체육관 66, 1018–1021 ~ 1998
• "자이로스코프로서의 오토바이", J. 히비, Am. J. 체육 42, 701–702
• 일상의 현상의 물리학, W. T. 그리피스, McGraw-Hill, 1998, 페이지 149–150.
• The Way Things Work, Macaulay, Houghton-Mifflin, New York, 1989년

종방향역학

자전거는 다양한 종방향 힘과 움직임을 경험할 수 있다.대부분의 자전거에서는 앞바퀴를 한쪽으로 돌리면 스티어링 축 각도와 트레일 양에 따라 후방 프레임 전체가 약간 앞으로 투구된다.^[9][47]앞, 뒤 또는 양쪽 모두 서스펜션이 있는 자전거에서는 트림이 자전거의 기하학적 구성을 설명하는데 사용되며, 특히 제동, 가속, 회전, 구동 열차 및 공기역학 드래그의 힘에 반응한다.^[9]

두 바퀴가 부담하는 하중은 질량 위치의 중심에 따라 달라지며, 차례로 승객 수, 짐의 양, 승객과 짐의 위치에 따라 달라질 뿐만 아니라 가속과 감속도 달라진다.이 현상은 ^[45][71]저자에 따라 하중 전달^[9] 또는 중량 전달이라고 알려져 있으며, 라이더와 디자이너 모두에게 도전과 기회를 제공한다.예를 들어, 오토바이 경주자들은 코너링 시 앞 타이어에 사용 가능한 마찰을 증가시키기 위해 이 마찰을 사용할 수 있으며, 급제동 시 프론트 서스펜션 압축을 줄이려는 시도는 여러 개의 오토바이 포크 설계를 발생시켰다.

순 공기역학 드래그 힘은 압력의 중심이라 불리는 단일 지점에서 작용하는 것으로 간주할 수 있다.^[45]고속에서는 리어 구동 휠에 대한 순 모멘트가 생성되고, 프론트 휠에서 리어 휠로 부하가 순전히 전달된다.^[45]또한 자전거의 모양과 설치될 수 있는 페어링의 모양에 따라 앞바퀴의 하중을 증가시키거나 감소시키는 공기역학적 리프트가 존재할 수 있다.^[45]

안정성

정지 상태에서 종방향으로 안정적이지만 충분한 가속이나 감속 하에서 자전거가 종방향으로 불안정해질 수 있으며, 오일러의 두 번째 법칙을 이용하여 지반 반응력을 분석할 수 있다.^[86]예를 들어 휠베이스 $L{\displaystyle }$ ${\displaystyle$ L$}$과(와$$) 높이 $h{\displaystyle }$ ${\displaystyle$ h$}$과(와) 후방$$ 휠 허브 $앞$ 거리$$b {\$displaystyle$b}에서 질량의 중심이 있는 자전거의 경우 바퀴에 가해지는 정상(수직형) 접지력 및 단순성을 위해 양쪽 휠이 잠긴 경우 다음과 같이 표현할 수 있다.^[9]

${\displaystyle N_{r}=mg\left({\frac {L-b}{L}}-\mu {\frac {h}{L}}\right)}$ for the rear wheel and ${\displaystyle N_{f}=mg\left({\frac {b}{$$앞바퀴$의 L$}+\mu {\frac {h}{L}\right)}$

마찰력(수평력)은 단순하다.

${\displaystyle F_{}}$ ${\displaystyle r_{}}$= 뒷바퀴의 경우$$ ${\displaystyle {\mu N}_{}}$ r ${\displaystyle$ F_{r}=\$mu N_{r}\,$ 앞바퀴의 경우$$ ${\displaystyle F_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle f_{}}$ $displaystyle F_{f}=\mu N_{f}\,$

여기서 $[\displaystyle \mu }$은 마찰 계수, m ${\displaystyle m}$은 자전거와 라이더의 총 질량, $g{\displaystyle }${\$displaysty$ g$}$은 중력의 가속이다.그러므로 만약

${\displaystyle \mu \geq {\frac {L-b}{h}},}$

질량의 중심이 앞바퀴 접촉 패치로부터 뒤로 연장되는 라인 위 또는 앞쪽에 있고 각도로 기울어진 경우

${\displaystyle \tan ^{-1}\왼쪽 사진\frac {1}{\mu }\오른쪽)\,}$

수평 위에서는 ^[45]후륜의 정상적인 힘이 0이 되고(이 때 방정식이 더 이상 적용되지 않음) 자전거가 앞바퀴 위로 뒤집히거나 앞으로 고리하기 시작한다.

반면 대부분의 탠덤 자전거나 롱휠베이스 리컴백 자전거는 물론 자동차 등 질량 높이의 중심이 라인 뒤나 아래에 있다면 앞바퀴가 자전거를 뒤집기에 충분한 제동력을 발생시킬 가능성이 적다.이는 타이어의 도로 부착력 한계까지 거의 감속할 수 있다는 것을 의미하며, 마찰계수가 0.8이면 0.8g에 달할 수 있어 최적의 조건에서도 직립자전거보다 40% 이상 높다.자전거 과학의 저자인 데이비드 고든 윌슨은 이로 인해 직립 자전거 타는 사람들이 차를 탈 경우 후방 추돌을 일으킬 위험에 처하게 된다고 지적한다.^[87]

마찬가지로, 강력한 오토바이는 바퀴라고 불리는 기동에서 앞바퀴를 지상에서 들어올릴 수 있을 만큼 뒷바퀴에 충분한 토크를 발생시킬 수 있다.제동 성능을 분석하기 위해 위에서 설명한 것과 유사한 선은 사용 가능한 마찰력, 질량 위치의 중심 및 충분한 동력을 고려하여 휠리가 가능한지 여부를 예측하기 위해 후륜 접촉 패치에서 그릴 수 있다.^[45]이러한 현상은 자전거에서도 일어날 수 있다. 비록 이용 가능한 전력이 훨씬 적지만, 질량의 중심이 충분히 뒤로 또는 위로 올라가거나 페달을 밟을 때 운전자가 뒤로 기어들어간다면 말이다.^[88]

물론 지형의 각도는 위의 모든 계산에 영향을 미칠 수 있다.다른 모든 것은 동일하게 유지되며, 언덕을 올라갈 때는 앞쪽 끝을 넘어 투구할 위험이 감소하고 언덕을 내려갈 때는 더 높아진다.힐을 타고 올라갈 때 휠라이를 할 가능성이 높아지며 오토바이 힐클라이밍 대회의 주요 요인이다.^[88]

접지 조건에 따른 제동

제동 시, 주행 중인 탑승자는 승차자와 자전거의 결합 질량 m의 속도 변화를 모색한다.이것은 여행에서 A의 마이너스 가속이다.F=ma, 가속 a는 질량 m에 관성 전방 힘 F를 발생시킨다.제동 a는 초기 속도 u에서 최종 속도 v까지, 시간 t에 걸쳐 있다.u - v = at 등식은 가속도가 클수록 속도 변화에 필요한 시간이 짧아진다는 것을 의미한다.정지 거리 s는 가속도 a가 도로 조건과 호환 가능한 가장 높은 값에 있을 때 가장 짧다: a가 높고 t가 낮을 때 s = ut + 1/2의² 방정식이 s를 낮춘다.

각 휠에 적용할 제동력은 지반 상태와 각 순간의 휠 무게 균형에 따라 달라진다.총 제동력은 승차자의 중력을 초과할 수 없고 자전거는 지면 타이어 마찰 μ의 계수를 곱한다. mg μ >= Ff + Fr.미끄럼은 Ff over Nf 또는 Fr over Nr의 비율이 μ보다 크면 발생하며, 후륜 미끄럼은 측면 안정성에 부정적인 영향을 덜 미친다.

제동할 때, 관성력은 f와 공동 선형이 아닌 이동 선에서 ma가 f 주위에 회전하는 경향이 있다.이러한 회전 경향, 즉 뒤집히는 순간은 mg로부터 한순간에 저항을 받는다.

한 인스턴스에서 프론트 휠 접촉 지점에 대한 잠시의 시간:

• 제동력이 없을 때 질량 m은 일반적으로 앞바퀴와 뒷바퀴 사이의 3분의 2 정도 되는 하단 브래킷 위에 있으며, 따라서 Nr은 Nf보다 크다.
• 지속적인 경량 제동에서는 비상 정지가 필요하지 않기 때문에 또는 열악한 지상 조건이 중제동을 방해하기 때문에 리어 휠에 여전히 많은 중량이 놓여 있는데, 이는 Nr이 여전히 크고 Fr이 a에 기여할 수 있다는 것을 의미한다.
• 제동 a가 증가하면 모멘트 mah가 증가하기 때문에 Nr과 Fr은 감소한다.최대 상수 a에서는 시계 방향과 시계 반대 방향 모멘트가 같으며, 이때 Nr = 0이다.더 큰 Ff는 정지작업을 개시한다.
  

  최대 제동 시 Nr = 0

기타 요인:

• 내리막길에서는 경사가 mg 라인을 f에 가깝게 이동시키기 때문에 앞바퀴 위로 넘어지는 것이 훨씬 쉽다.이러한 경향을 줄이기 위해 기수는 페달을 뒤로 물러서서 가능한 한 멀리 떨어져 있도록 할 수 있다.
• 제동력이 증가할 때 질량 m의 중심이 자전거에 비해 전방으로 이동할 수 있으며, 자전거가 앞 바퀴에 서스펜션이 있을 경우 앞 바퀴가 하중 하에서 압축되어 자전거 형상이 변경된다.이 모든 것이 앞바퀴에 추가 하중을 가한다.
• 브레이크 조작이 끝나면 운전자가 정지할 때 서스펜션이 풀리면서 승차자를 뒤로 밀어낸다.

μ에 대한 값은 여러 요인에 따라 크게 달라진다.

• 지면 또는 노면이 만들어지는 재료.
• 땅이 젖어 있든 말든.
• 지면이 매끈하거나 거칠다.
• 땅의 단단함 또는 느슨함.
• 마찰력이 50km/h(30mph) 이상으로 감소하는 차량 속도.
• 마찰이 롤링인지 슬라이딩인지 여부. 슬라이딩 마찰은 피크 롤링 마찰보다 최소 10% 낮음.^[89]

제동

표준 직립 자전거의 제동력은 대부분 앞바퀴에서 나온다.위의 분석에서 알 수 있듯이 브레이크 자체가 충분히 강하면 뒷바퀴가 미끄러지기 쉬운 반면 앞바퀴는 종종 승차자와 자전거를 앞바퀴 위로 뒤집기에 충분한 정지력을 발생시킬 수 있다.이것은 뒷바퀴를 들어 올려도 자전거가 뒤집히지 않으면 스토피(stoppie)라고 하고, 자전거가 뒤집히면 엔도(약칭 endo-over-end)라고 한다.그러나 크루저 오토바이와^[90] 리컴백 자전거와 같은 길고 낮은 자전거에서는 앞 타이어가 대신 미끄러져 균형을 잃을 수 있다.밸런스 상실이 없다고 가정하면 자전거의 기하학적 구조, 자전거와 승차자의 무게중심 위치, 최대 마찰계수에 따라 최적의 제동성능을 계산할 수 있다.^[91]

전면 서스펜션, 특히 텔레스코핑 포크 튜브의 경우 제동 중 앞바퀴의 하방력이 증가하면 서스펜션이 압축되고 앞쪽 끝이 낮아질 수 있다.이것은 브레이크 다이빙이라고 알려져 있다.제동력이 앞바퀴의 하강력을 높이는 방법을 활용하는 라이딩 기법을 트레일 브레이크라고 한다.

프론트 휠 브레이크

프론트 휠 브레이크의 최대 감속 제한 인자는 다음과 같다.

• 타이어와 지면 사이의 정적 마찰의 최대 제한 값(건식 아스팔트 고무의 경우 0.5에서 0.8 사이)^[92]
• 브레이크 패드와 림 또는 디스크 사이의 운동 마찰
• (자전거와 라이더의) 앞바퀴 위로 피칭 또는 루핑을 한다.

브레이크가 뛰어난 건조한 아스팔트 위에서 똑바로 선 자전거의 경우, 피칭이 아마도 제한 요인이 될 것이다.일반적인 직립 자전거와 승차자의 질량의 결합 중심은 앞바퀴 접촉 패치로부터 약 60cm(24인치), 위 120cm(47인치)로 최대 0.5g(5m/s² 또는 16ft/s²)의 감속이 허용된다.^[28]하지만 운전자가 브레이크를 제대로 조절하면 피칭을 피할 수 있다.기수가 체중을 앞뒤로 움직이면 더 큰 감속이 가능하다.

많은 값싼 자전거의 전면 브레이크는 충분히 강력하지 않기 때문에, 도로에서는, 그것들이 제한적인 요인이다.값싼 캔틸레버 브레이크, 특히 "파워 조절기"와 롤리 스타일의 사이드 풀 브레이크는 제동력을 심하게 제한한다.젖은 상태에서는 그것들은 훨씬 덜 효과적이다.앞바퀴 미끄럼틀은 오프로드에서 더 흔하다.진흙, 물, 느슨한 돌은 타이어와 트레일 사이의 마찰을 줄여주지만, 노브 타이어는 표면의 불규칙성을 잡음으로써 이러한 효과를 완화시킬 수 있다.앞바퀴 미끄럼틀은 도로든 오프든 코너에서도 흔히 볼 수 있다.구심 가속은 타이어-지반 접촉에 가해지는 힘을 더하고 마찰력이 휠 미끄럼틀을 초과할 때 힘을 더한다.

후륜제동

직립 자전거의 후방 브레이크는 위에서 설명한 대로 후륜에서 정상적인 힘이 감소하기 때문에 기껏해야 0.25g(~2.5m/s²)의 감속만 발생시킬 수 있다.^[87]예를 들어, 코스터 브레이크만 장착된 자전거와 다른 브레이크 메커니즘이 없는 고정 기어 자전거는 모두 이러한 제한을 받는다.그러나 후륜 제동을^[93] 보장할 수 있는 상황이 있다.

• 미끄러운 표면 또는 울퉁불퉁한 표면.앞바퀴 제동 시 마찰계수가 낮아지면 앞바퀴가 미끄러져 균형을 잃게 되는 경우가 많다.^[93]
• 프론트 펑크 난 타이어.타이어가 펑크 난 휠을 제동하면 타이어가 림에서 떨어져 마찰을 크게 줄일 수 있으며, 앞바퀴의 경우 밸런스 상실을 초래할 수 있다.^[93]
• 고의적으로 리어 휠 미끄럼을 유도하여 오버스티어를 유도하고 턴 반경이 좁은 경우
• 프론트 브레이크 ^[93]고장
• 뒤로 젖혀지는 자전거.롱 휠베이스 리컴백은 CG가 리어 휠 근처에 있기 때문에 양호한 리어 브레이크가 필요하다.^[94]

제동기법

전문가 의견은 "처음에는 양쪽 레버를 균등하게 사용"^[95]에서 "일반적인 휠베이스의 자전거를 멈출 수 있는 가장 빠른 속도는 앞 브레이크를 너무 세게 작동시켜 뒷바퀴가 지면에서 막 들어올리려고 할 때"^[93]로 다양하다.

현수

자전거는 측면 준수를 고려하기는 하지만, 대칭의 중심면에서 주로 작동하는 전면, 후면, 전면 서스펜션 또는 서스펜션이 없을 수 있다.^[45]자전거 서스펜션의 목표는 승차자가 경험하는 진동을 줄이고, 지면과 바퀴 접촉을 유지하며, 물체를 탈 때 운동량의 손실을 줄이고, 점프나 낙하로 인한 충격력을 줄이고, 차량 트림을 유지하는 것이다.^[9]1차 서스펜션 매개변수는 강성, 댐핑, 스프링 및 언스프링 질량, 타이어 특성이다.^[45]지형의 불규칙성 외에도 브레이크, 가속 및 구동렬 힘도 위에서 설명한 대로 서스펜션을 작동시킬 수 있다.자전거에 대한 밥과 페달 피드백, 모터사이클에 대한 샤프트 효과, 스쿼트 및 브레이크 다이빙 등이 그 예다.

진동

자전거의 진동 연구에는 엔진 밸런스,^[96] 휠 밸런스,^[97] 지상 표면 및 공기역학, 변속 및 흡수, 자전거, 승차자 및 안전에 미치는 영향 등의 원인이 포함된다.진동 분석에서 중요한 요소는 시스템의 자연 주파수와 진동 발생원의 가능한 구동 주파수를 비교하는 것이다.^[98]근접전은 큰 진폭을 일으킬 수 있는 기계적 공명을 의미한다.진동 감쇠의 과제는 동력 전달 및 취급에 필요한 프레임 강성을 희생시키지 않고 특정 방향(수직)에서 준수를 만드는 것이다.^[99]자전거 진동의 또 다른 문제는 물질적^[100] 피로로 인한 고장 가능성이다 승차자에게 미치는 진동의 영향은 불편함, 효율성의 상실, 레이노우드의 2차적 형태인 손팔진동증후군, 전신진동 등이다.진동 계측기는 부정확하거나 읽기 어려울 수 있다.^[100]

자전거로

제대로 작동하는 자전거에서 진동의 주된 원인은 자전거가 굴러가는 표면이다.공압 타이어와 전통적인 자전거 정지장치 외에도, 주행자에게 도달하기 전에 진동을 축축하게 하는 다양한 기술이 개발되었다.여기에는 전체 프레임 또는 전면 포크, 시트 포스트 또는 핸들 바와 같은 주요 구성 요소와 같은 탄소 섬유와 같은 재료, 커브 시트 스테이와 같은 튜브 모양,^[101] 젤 핸들 바 그립과 새들 및 특수 삽입물(예: 전문화된 Zertz,^[102][103] Bontrager의 Buzzzkills) 등이 포함된다.

오토바이 안에서

노면 외에도 오토바이 진동은 엔진과 바퀴에 의해 발생할 수 있다.제조업체는 엔진 밸런스축, 고무 엔진 마운트,^[104] 타이어 중량 등 이러한 진동을 감소시키거나 감쇠시키기 위해 다양한 기술을 사용한다.^[105]진동이 야기하는 문제는 또한 진동을 줄이기 위해 설계된 애프터마켓 부품과 시스템의 산업을 야기시켰다.추가 기능에는 핸들 바 중량,^[106] 분리된 풋 페그, 엔진 카운터 웨이트 등이 포함된다.고속에서, 오토바이와 그들의 라이더들은 또한 공기역학적 동요나 뷔페팅을 경험할 수 있다.^[107]이것은 윈드실드와 같은 주요 부품의 공기 흐름을 변화시킴으로써 줄일 수 있다.^[108]

실험

자전거 역학에 대한 다양한 가설을 검증하거나 반증하기 위해 다양한 실험이 수행되었다.

• 데이비드 존스는 상속할 수 없는 구성을 찾기 위해 여러 대의 자전거를 만들었다.^[6]
• 리처드 클라인은 존스의 연구 결과를 확인하기 위해 여러 대의 자전거를 만들었다.^[5]
• 리처드 클라인도 조향 토크와 그 영향을 조사하기 위해 '토크 렌치 바이크'와 '로켓 바이크'를 만들었다.^[5]
• 키스 코드는 승차자의 움직임과 위치가 조향에 미치는 영향을 조사하기 위해 핸들 바가 고정된 오토바이를 만들었다.^[109]
• 슈와브와 쿠이즈만은 계기 자전거로 치수를 측정했다.^[110]
• Hubbard와 Moore는 계기 자전거로 측정을 해 왔다.^[111]

참고 항목

참조

추가 읽기

• '자전거 기하학 및 핸들링 소개', 칼 앤더슨
• '자전거를 똑바로 세우는 것은 무엇인가?' 잡스트 브란트의 작품
• 존 포레스터의 '다혼 자전거의 안정성에 관한 보고서'

외부 링크

동영상:

• 무임승차 자전거의 자기 안정성 입증 비디오
• 자전거가 떨어지지 않는 이유: TEDx Delft 2012의 아렌드 슈워브
• 워블 무비 (AVI)
• 위브 무비(AVI)
• 웨이블 크래시(플래시)
• 사이언스 프라이데이 비디오

연구 센터:

• 델프트 공과대학교 자전거 다이내믹스
• 코넬 대학교 자전거 역학
• 일리노이 대학교 자전거 과학
• 파도바 대학교의 모터사이클 역학
• 임페리얼 칼리지 컨트롤 및 파워 연구단
• UC Davis의 자전거 역학, 제어 및 취급
• 위스콘신 밀워키 대학 자전거 및 오토바이 공학 연구실

컨퍼런스:

• 자전거 및 모터사이클 다이내믹스 2010: 2010년 10월 20일-22일, 델프트 공과대학 단일 트랙 차량의 동적 및 제어에 관한 심포지엄
• DSCC 2012의 단일 트랙 차량 동력학: 2012년 10월 17~19일 미국 플로리다주 포트로더데일에서 열린 ASME 다이내믹 시스템 및 제어 컨퍼런스에서 두 세션
• 2013년 자전거 및 모터사이클 다이내믹스: 2013년 11월 11일~13일 니혼대학교 단일 트랙 차량의 동적 및 제어에 관한 심포지엄
• 자전거 및 오토바이 동력학 2016: 2016년 9월 21-23일 위스콘신-밀워키 대학교 싱글 트랙 차량의 동적 및 제어에 관한 심포지엄
• 자전거 및 모터사이클 다이내믹스 2019: 싱글 트랙 차량의 역동성과 제어에 관한 심포지엄, 2019년 9월 9일–11일, 파도바 대학교
• 자전거 및 모터사이클 다이내믹스 컨퍼런스:요약 페이지