삼각헤베노로툰다

삼각헤베노로툰다
유형	존슨 J91 - J92 - J1
얼굴	13개의 삼각형 정사각형 3개 펜타곤 3개 육각형 1개
가장자리	36
정점	18
꼭지점 구성	3(33.5) 6(3.4.3.5) 3(3.5.3.5) 2.3(32.4.6)
대칭군	C3v
이중 다면체	-
특성.	볼록하게 하다
그물

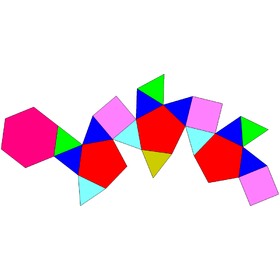기하학에서 삼각형 헤베페노로툰다는 존슨 고형물(J₉₂)의 하나이다.

존슨 고체는 일반 폴리곤 면으로 구성되지만 균일한 폴리헤드라(Platonic 고형물, 아르키메데스 고형물, 프리즘 또는 항정신병)가 아닌 92개의 엄격히 볼록한 폴리헤드라 중 하나이다.그것들은 1966년에 처음으로 이 다면체들을 나열한 노먼 존슨이 이름을 지었다.^[1]

그것은 플라토닉과 아르키메데스 고형물의 "절단과 붙여넣기" 조작에서 발생하지 않는 존슨 고형물 중 하나이다.그러나, 그것은 아르키메데스 고체인 이코시다데카헤드론과 강한 관계를 가지고 있다.가장 확실한 것은 고체의 한쪽에 있는 3개의 펜타곤과 4개의 삼각형으로 이루어진 군집이다.만약 이 얼굴들이 이코시다데카헤드론에 있는 얼굴들의 일치된 조각과 일직선으로 정렬된다면, 육각형 얼굴은 이코시다데카헤드론의 두 반대되는 삼각형 면 사이의 중간에 평면에 놓여질 것이다.

삼각형 헤베페노로툰다(Hebesphernotunda)는 또한 롬비코시도데카헤드론(Rhombicosidodecacahedron)의 해당 면과 정렬할 수 있는 얼굴 군집을 가지고 있는데, 각각은 사각형 삼각형과 정사각형에 인접한 두 개의 항정신병 삼각형으로 구성되어 있다.

각(3.5³) 꼭지점 주위의 얼굴도 다양한 감소된 이코사헤드라의 해당 얼굴과 정렬할 수 있다.

존슨은 hebespheno-라는 접두사를 사용하여 세 개의 인접한 LUN에 의해 형성된 뭉툭한 쐐기 모양의 콤플렉스를 가리키는데, 룬은 정삼각형이 반대편에 붙어 있는 사각형이다.접미사(삼각형) -로툰다(rotunda)는 3개의 정삼각형과 또 다른 정삼각형을 둘러싸고 있는 3개의 정삼각형 5각형의 복합체를 말하는데, 이는 오각형 로툰다와 구조적으로 유사하다.^[1]

삼각형 모양의 헤베스피노툰다는 3, 4, 5, 6면의 얼굴을 가진 유일한 존슨의 골격이다.

데카르트 좌표, 평행 좌표.

가장자리 길이 √5 – 1의 삼각형 헤베페노로툰다에 대한 데카르트 좌표는 점의 궤도 결합에 의해 주어진다.

${\displaystyle \left(0,-{\frac {2}{\tau {\sqrt {3}}}},{\frac {2\tau }{\sqrt {3}}}\right),\left(\tau ,{\frac {1}{{\sqrt {3}}\tau ^{2}}},{\frac {2}{\sqrt {3}}}\right),}$

${\displaystyle \left(\tau ,-{\fract {3}},{\prac {2}{\sqrt{3}\}\{\sqrt}\}\좌측\frac {2}{}}}}{\0,0\오른쪽)}$

z축을 중심으로 120° 회전하여 생성된 그룹의 작용과 yz 평면에 대한 반사.^[2]여기, 𝜏 =√5 + 1/2(때로는 φ)이 황금비율이다.첫 번째 점은 육각형의 반대쪽에 삼각형을 생성하고, 두 번째 점은 이전 삼각형을 둘러싼 삼각형의 밑동을 생성하고, 세 번째 점은 첫 번째 삼각형의 반대쪽에 있는 펜타곤의 끝을 생성하고, 마지막 점은 육각형을 생성한다.

그런 다음 가장자리 길이의 삼각형 헤베페노로툰다의 표면적을 다음과 같이 계산할 수 있다.

${\displaystyle A=\left(3+{\frac {1}{4}}{130+90{\sqrt{5}}}}}{750+30{5}}}}\sqrt{5}}}}}a^{2}\약 16.38867a^{2},},}$^[3]

그리고 그 부피는 다음과 같다.

${\displaystyle V={\frac{1}{6}\왼쪽(15+7{\sqrt{5}\오른쪽)a^{3}\약 5.10875a^{3}.}$^[4]

두 번째, 반전된 삼각형 헤베페노로툰다는 각 점의 두 번째와 세 번째 좌표를 부정함으로써 얻을 수 있다.이 두 번째 다면체는 일반적인 육각형 얼굴에서 첫 번째 다면체와 결합될 것이며, 쌍은 이코시다데카면체를 내접할 것이다.육각면체를 황금비율로 스케일링하면 결과의 볼록한 선체가 전체 이코시다데카헤드론(icocosidodechahedron)이 된다.

참조

외부 링크

• Eric W. Weisstein, Triangular hebesphenorotunda (Johnson solid) at MathWorld.