| Jn | 견실명 | 이미지 | 꼭짓점 | 가장자리 | 얼굴들 | 대칭군과 그 순서 | 표면적과 부피 |
| 1 | 등변의
광장
피라미드의 |  | 5 | 8 | 5 | 8위의4v C |  |
| 2 | 오각형
피라미드의 |  | 6 | 10 | 6 | 주문5v 10의 C |  |
| 3 | 삼각형
큐폴라 |  | 9 | 15 | 8 | 6위의3v C |  |
| 4 | 광장
큐폴라 |  | 12 | 20 | 10 | 8위의4v C |  |
| 5 | 오각형
큐폴라 |  | 15 | 25 | 12 | 주문5v 10의 C |  |
| 6 | 오각형
로툰다 |  | 20 | 35 | 17 | 주문5v 10의 C |  |
| 7 | 길쭉한
삼각형의
피라미드의 |  | 7 | 12 | 7 | 6위의3v C |  |
| 8 | 길쭉한
광장
피라미드의 |  | 9 | 16 | 9 | 8위의4v C |  |
| 9 | 길쭉한
오각의
피라미드의 |  | 11 | 20 | 11 | 주문5v 10의 C |  |
| 10 | 자이로롱드
광장
피라미드의 |  | 9 | 20 | 13 | 8위의4v C |  |
| 11 | 자이로롱드
오각의
피라미드의 |  | 11 | 25 | 16 | 주문5v 10의 C |  |
| 12 | 삼각형
바이피라미드의 |  | 5 | 9 | 6 | D3h of order 12 |  |
| 13 | 오각형
바이피라미드의 |  | 7 | 15 | 10 | D오더5h 20 |  |
| 14 | 길쭉한
삼각형의
바이피라미드의 |  | 8 | 15 | 9 | D3h of order 12 |  |
| 15 | 길쭉한
광장
바이피라미드의 |  | 10 | 20 | 12 | 16위의4h D |  |
| 16 | 길쭉한
오각의
바이피라미드의 |  | 12 | 25 | 15 | D오더5h 20 |  |
| 17 | 길쭉한
광장
바이피라미드의 |  | 10 | 24 | 16 | 16위의4d D |  |
| 18 | 길쭉한
삼각형의
큐폴라 | 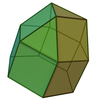 | 15 | 27 | 14 | 6위의3v C |  |
| 19 | 길쭉한
광장
큐폴라 | 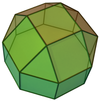 | 20 | 36 | 18 | 8위의4v C |  |
| 20 | 길쭉한
오각의
큐폴라 |  | 25 | 45 | 22 | 주문5v 10의 C |  |
| 21 | 길쭉한
오각의
로툰다 |  | 30 | 55 | 27 | 주문5v 10의 C |  |
| 22 | 자이로롱드
삼각형의
큐폴라 |  | 15 | 33 | 20 | 6위의3v C |  |
| 23 | 자이로롱드
광장
큐폴라 | 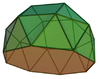 | 20 | 44 | 26 | 8위의4v C |  |
| 24 | 자이로롱드
오각의
큐폴라 |  | 25 | 55 | 32 | 주문5v 10의 C |  |
| 25 | 자이로롱드
오각의
로툰다 |  | 30 | 65 | 37 | 주문5v 10의 C |  |
| 26 | 자이로비파스티지움 |  | 8 | 14 | 8 | D2d of order 8 |  |
| 27 | 삼각형
정사성 유폴라 |  | 12 | 24 | 14 | D3h of order 12 |  |
| 28 | 광장
정사성 유폴라 |  | 16 | 32 | 18 | 16위의4h D |  |
| 29 | 광장
gyrobicupola |  | 16 | 32 | 18 | 16위의4d D |  |
| 30 | 오각형
정사성 유폴라 |  | 20 | 40 | 22 | D오더5h 20 |  |
| 31 | 오각형
gyrobicupola |  | 20 | 40 | 22 | D오더5d 20 |  |
| 32 | 오각형
오소쿠폴라로툰다 |  | 25 | 50 | 27 | 주문5v 10의 C |  |
| 33 | 오각형
자이로쿠폴라로툰다 |  | 25 | 50 | 27 | 주문5v 10의 C |  |
| 34 | 오각형
오르토비로툰다 |  | 30 | 60 | 32 | D오더5h 20 |  |
| 35 | 길쭉한
삼각형의
정사성 유폴라 |  | 18 | 36 | 20 | D3h of order 12 |  |
| 36 | 길쭉한
삼각형의
gyrobicupola |  | 18 | 36 | 20 | D3d of order 12 |  |
| 37 | 길쭉한
광장
gyrobicupola |  | 24 | 48 | 26 | 16위의4d D |  |
| 38 | 길쭉한
오각의
정사성 유폴라 |  | 30 | 60 | 32 | D오더5h 20 |  |
| 39 | 길쭉한
오각의
gyrobicupola |  | 30 | 60 | 32 | D오더5d 20 |  |
| 40 | 길쭉한
오각의
오소쿠폴라로툰다 |  | 35 | 70 | 37 | 주문5v 10의 C |  |
| 41 | 길쭉한
오각의
자이로쿠폴라로툰다 |  | 35 | 70 | 37 | 주문5v 10의 C |  |
| 42 | 길쭉한
오각의
오르토비로툰다 |  | 40 | 80 | 42 | D오더5h 20 |  |
| 43 | 길쭉한
오각의
자이로로툰다 |  | 40 | 80 | 42 | D오더5d 20 |  |
| 44 | 자이로롱드
삼각형의
쌍태아 |  | 18 | 42 | 26 | 순서3 6의 D |  |
| 45 | 자이로롱드
광장
쌍태아 |  | 24 | 56 | 34 | D4 of order 8 |  |
| 46 | 자이로롱드
오각의
쌍태아 |  | 30 | 70 | 42 | 차수 10의5 D |  |
| 47 | 자이로롱드
오각의
컵폴라로툰다 |  | 35 | 80 | 47 | C오더5 5 |  |
| 48 | 자이로롱드
오각의
비로툰다 |  | 40 | 90 | 52 | 차수 10의5 D |  |
| 49 | 증강
삼각형의
프리즘 | 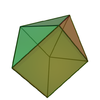 | 7 | 13 | 8 | 4위의2v C |  |
| 50 | 바이오션드
삼각형의
프리즘 |  | 8 | 17 | 11 | 4위의2v C |  |
| 51 | Triaugmented
삼각형의
프리즘 |  | 9 | 21 | 14 | D3h of order 12 |  |
| 52 | 증강
오각의
프리즘 | 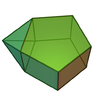 | 11 | 19 | 10 | 4위의2v C |  |
| 53 | 바이오션드
오각의
프리즘 | 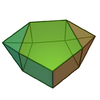 | 12 | 23 | 13 | 4위의2v C |  |
| 54 | 증강
육각형의
프리즘 | 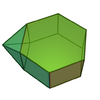 | 13 | 22 | 11 | 4위의2v C |  |
| 55 | 파라비 증강
육각형의
프리즘 | 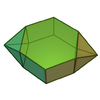 | 14 | 26 | 14 | D2h of order 8 |  |
| 56 | 메타비아증강
육각형의
프리즘 | 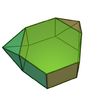 | 14 | 26 | 14 | 4위의2v C |  |
| 57 | Triaugmented
육각형의
프리즘 |  | 15 | 30 | 17 | D3h of order 12 |  |
| 58 | 증강
십이십면체 | 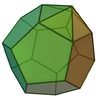 | 21 | 35 | 16 | 주문5v 10의 C |  |
| 59 | 파라비 증강
십이십면체 |  | 22 | 40 | 20 | D오더5d 20 |  |
| 60 | 메타비아증강
십이십면체 |  | 22 | 40 | 20 | 4위의2v C |  |
| 61 | Triaugmented
십이십면체 | 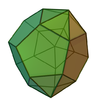 | 23 | 45 | 24 | 6위의3v C |  |
| 62 | 메타비디아가 감소하였습니다.
20면체의 |  | 10 | 20 | 12 | 4위의2v C |  |
| 63 | 트리디미니스트
20면체의 |  | 9 | 15 | 8 | 6위의3v C |  |
| 64 | 증강
삼수의
20면체의 | 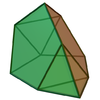 | 10 | 18 | 10 | 6위의3v C |  |
| 65 | 증강
잘린
사면체의 |  | 15 | 27 | 14 | 6위의3v C |  |
| 66 | 증강
잘린
정육면체 |  | 28 | 48 | 22 | 8위의4v C |  |
| 67 | 바이오션드
잘린
정육면체 |  | 32 | 60 | 30 | 16위의4h D |  |
| 68 | 증강
잘린
십이십면체 | 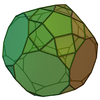 | 65 | 105 | 42 | 주문5v 10의 C |  |
| 69 | 파라비 증강
잘린
십이십면체 | 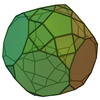 | 70 | 120 | 52 | D오더5d 20 |  |
| 70 | 메타비아증강
잘린
십이십면체 |  | 70 | 120 | 52 | 4위의2v C |  |
| 71 | Triaugmented
잘린
십이십면체 |  | 75 | 135 | 62 | 6위의3v C |  |
| 72 | 자이레이트
마름모 십이면체 |  | 60 | 120 | 62 | 주문5v 10의 C |  |
| 73 | Parabigyrate
마름모 십이면체 |  | 60 | 120 | 62 | D오더5d 20 |  |
| 74 | 대사율
마름모 십이면체 |  | 60 | 120 | 62 | 4위의2v C |  |
| 75 | 트리기레이트
마름모 십이면체 |  | 60 | 120 | 62 | 6위의3v C |  |
| 76 | 축소
마름모 십이면체 |  | 55 | 105 | 52 | 주문5v 10의 C |  |
| 77 | 파라자일레이트
축소된
마름모 십이면체 |  | 55 | 105 | 52 | 주문5v 10의 C |  |
| 78 | 메타기레이트
축소된
마름모 십이면체 |  | 55 | 105 | 52 | 순서s 2의 C |  |
| 79 | 비기레이트
축소된
마름모 십이면체 |  | 55 | 105 | 52 | 순서s 2의 C |  |
| 80 | 파라비드 감소
마름모 십이면체 |  | 50 | 90 | 42 | D오더5d 20 |  |
| 81 | 메타비디아가 감소하였습니다.
마름모 십이면체 |  | 50 | 90 | 42 | 4위의2v C |  |
| 82 | 자이레이트
비디미티드의
마름모 십이면체 |  | 50 | 90 | 42 | 순서s 2의 C |  |
| 83 | 트리디미니스트
마름모 십이면체 |  | 45 | 75 | 32 | 6위의3v C |  |
| 84 | 스너브
디스페노이드 |  | 8 | 18 | 12 | D2d of order 8 |  |
| 85 | 스너브
광장
반제국주의 |  | 16 | 40 | 26 | 16위의4d D |  |
| 86 | Sphenocorona |  | 10 | 22 | 14 | 4위의2v C |  |
| 87 | 증강
sphenocorona |  | 11 | 26 | 17 | 순서s 2의 C |  |
| 88 | Sphenomegacorona |  | 12 | 28 | 18 | 4위의2v C |  |
| 89 | Hebesphenomegacorona |  | 14 | 33 | 21 | 4위의2v C |  |
| 90 | 디스페노큘레이션 | 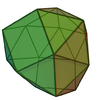 | 16 | 38 | 24 | D2d of order 8 |  |
| 91 | 빌루나비로툰다 |  | 14 | 26 | 14 | D2h of order 8 |  |
| 92 | 삼각형
헤베스페노로툰다 |  | 18 | 36 | 20 | 6위의3v C |  |