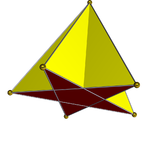
오각형 피라미드

오각형 피라미드
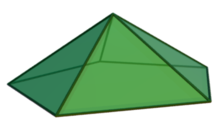유형	존슨 J1 - J2 - J3
얼굴	삼각형 5개 1오각형
가장자리	10
정점	6
꼭지점 구성	5(32.5) (35)
슐레플리 기호	( ) ∨ {5}
대칭군	C5v, [5], (*55)
회전군	C5, [5]+, (55)
이중 다면체	자아의
특성.	볼록하게 하다
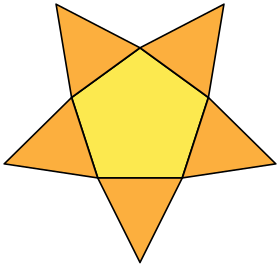
그물

기하학에서, 오각형 피라미드는 오각형의 기초가 있는 피라미드로, 한 지점(정점)에서 만나는 다섯 개의 삼각형 면이 세워진다.다른 피라미드처럼, 그것은 자기 이중적이다.

일반 오각형 피라미드에는 정삼각형인 정삼각형, 정삼각형인 정삼각형, 정삼각형인 정삼각형, 정삼각형인 정삼각존슨 고형물(J₂) 중 하나이다.

그것은 이코사면체의 "Lid"로 볼 수 있으며, 나머지 이코사면체는 오각형 피라미드를 형성하고₁₁ 있다.

보다 일반적으로 순서-2 꼭지점 통일형 오각형 피라미드는 일반 오각형 베이스와 5개의 이등변 삼각형 면으로 정의할 수 있다.

데카르트 좌표, 평행 좌표.

오각형 피라미드는 일반적인 이코사면체의 "Lid"로 볼 수 있다. 나머지 이코사면체는 교량화된 오각형 피라미드를 형성한다. J₁₁. 이코사면체의 카르테시아 좌표에서 가장자리 길이 2의 오각형 피라미드의 좌표는 다음과 같이 추정할 수 있다.

${\displaystyle (1,0,\tau )\,\,(-1,\tau,1)\,(0,\tau,1),\,(\tau,-1,0),(\tau,-1),(0,-\tau,1)}$

여기서 𝜏(때로는 φ)은 황금비율이다.^[1]

따라서 가장자리 길이가 a인 오각형 피라미드의 높이 H는 오각형 면의 중간점에서 정점까지 다음과 같이 계산할 수 있다.

${\displaystyle H=\왼쪽({\sqrt {5-{\sqrt{5}}{10}}\오른쪽)a\약 0.52573a.}$^[2]

그것의 표면적 A는 오각형 베이스의 면적에 하나의 삼각형 면적의 5배를 더한 것으로 계산할 수 있다.

${\displaystyle A={\frac{a^{2}}:{\sqrt{5}{5}}}{{5}}}}\좌측(10+{\sqrt{5}}}}}}}{75+30{\sqrt{5}}\sqrt{5}}\cdot a^{2}}.}$^[3][2]

그것의 부피는 다음과 같이 계산할 수 있다.

${\displaystyle V=\왼쪽({\frac {5+{\sqrt{5}}{24}}}}{24}\오른쪽)a^{3}\약 0.30150a^{3}.}$^[3]

관련 다면체

펜타그램 스타 피라미드는 정점 배열이 동일하지만 펜타그램 베이스에 연결된다.

일반 피라미드
디조날	삼각형	사각형	오각형	육각형	헵타곤	팔각형	엔네오각형	십각형...
부적절한	정규	등각형		이소셀레스

오각형 좌굴은 꼭지가 잘린 오각형 피라미드다.

이코사면체의 꼭대기는 오각형 피라미드다.

예

참조

외부 링크

• Eric W. Weisstein, Pentagonal pyramid (Johnson solid) at MathWorld.
• Virtual Reality Polyedra www.georgehart.com:폴리헤드라 백과사전 (VRML 모델)