삼각직교공포증
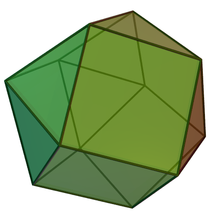
Triangular orthobicupola| 삼각직교공포증 | |
|---|---|
 | |
| 유형 | 존슨 J26 - J27 - J28 |
| 얼굴 | 2+6 삼각형 6제곱 |
| 가장자리 | 24 |
| 정점 | 12 |
| 꼭지점 구성 | 6(32.42) 6(3.4.3.4) |
| 대칭군 | D3h |
| 이중 다면체 | 트라페조롬 도데카헤드론 |
| 특성. | 볼록하게 하다 |
| 그물 | |
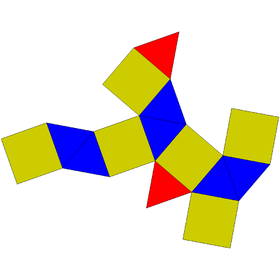 | |
기하학에서 삼각형 Orthobisupola는 Johnson 고형물(J27)의 하나이다.이름에서 알 수 있듯이, 두 개의 삼각형 큐폴라(J3)를 베이스에 붙여서 만들 수 있다.각 꼭지점에 동일한 수의 정사각형과 삼각형을 가지고 있지만 정점 변환은 아니다.반투옥타헤드론, 꼬인 큐보톡타헤드론 또는 헝클어진타헤드론이라고도 한다.그것은 또한 표준 다면체다.
존슨 고체는 일반 폴리곤 면으로 구성되지만 균일한 폴리헤드라(Platonic 고형물, 아르키메데스 고형물, 프리즘 또는 항정신병)가 아닌 92개의 엄격히 볼록한 폴리헤드라 중 하나이다.그것들은 1966년에 처음으로 이 다면체들을 나열한 노먼 존슨이 이름을 지었다.[1]
삼각형 정형외과는 무한정 일련의 정형외과의 첫 번째 것이다.
큐보타헤드라와의 관계
| 삼각직교공포증 | 삼각형 자이로비큐폴라 |
|---|---|
 |  |
| 삼각형 오르토비큐폴라와 큐옥타헤드론(삼각형 자이로비큐폴라)은 모두 중심 정규 육각형을 포함하고 있다.그들은 이 육각형 위에서 삼각형 큐폴레 한 쌍으로 해부될 수 있다. | |
삼각형 오르토비큐폴라는 존슨의 고형물 명칭에서 삼각형 자이로비큐폴라라고 알려져 있는 큐보타헤드론과 표면적으로 유사하다 - 차이점은 삼각형 오르토비큐폴라를 구성하는 두 개의 삼각형 큐폴라가 결합되어 짝을 이루는 옆면(헨체, "정체"; 큐보헤드론)이 결합되어 있다는 것이다.삼각형이 정사각형에 맞도록 결합되어 있고 그 반대도 마찬가지다.삼각형 직교공포증인 경우 접합 전 큐폴라 1개를 60도 회전시키면 큐폭타헤드론이 나온다.따라서 삼각형 정형외과의 또 다른 이름은 항우두옥타헤드론이다.
이 고체를 길쭉하게 하여 만들어진 길쭉한 삼각형 직교부폴라(J35)는 롬비쿠보옥타헤드론과 (다른) 특별한 관계를 가지고 있다.
삼각형 직교공포증의 이중은 사다리꼴-롬방 도데카헤드론이다.롬빅 6개와 사다리꼴 6개를 가지고 있으며, 롬빅 도데카헤드론과 비슷하다.
포뮬라과
모든 면이 정규이고 가장자리 길이가 a인 경우 부피, 표면 면적 및 회반도에 대해 다음과 같은 공식을 사용할 수 있다.[2]
삼각형 직교공포증(triangle Orthobisupola)의 회선(curradius)은 가장자리 길이(C = a
관련 다면체 및 허니컴
정류된 입방체 벌집형 벌집은 삼각형 직교성형 및 사각 피라미드의 공간을 채우는 격자로 분해하여 다시 지을 수 있다.[3]
참조
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- ^ Stephen Wolfram, Wolfram Alpha의 "삼각형 직교포비아폴라".2010년 7월 23일 회수.
- ^ "J27 honeycomb".




