삼각형 범주

수학에서 삼각형 범주는 "번역 펑터"의 추가 구조와 "정확한 삼각형"의 클래스를 가진 범주다.대표적인 예가 안정된 호모토피 범주뿐만 아니라 아벨리아 범주의 파생 범주다.정확한 삼각형은 아벨의 범주에서 짧은 정확한 시퀀스뿐만 아니라 위상의 섬유질 시퀀스와 코파이버 시퀀스를 일반화한다.

많은 동질적 대수학들이 삼각형 범주의 언어에 의해 명확해지고 확장되는데, 중요한 예는 피복 코호몰로지 이론이다.1960년대에, 일반적으로 삼각형 범주의 사용은 공간 X에 있는 피복의 특성을 X에 있는 피복의 파생 범주의 개체로 간주되는 피복의 복합체까지 확장하는 것이었다.보다 최근에는 삼각형 범주가 그들 자신의 권리로 관심의 대상이 되고 있다.서로 다른 기원의 삼각형 범주들 사이의 많은 등가성이 증명되거나 추측되었다.예를 들어, 동질 거울 대칭 추측은 Calabi-의 파생 범주를 예측한다.Yau 매니폴드는 "거울" 동시 다지관의 후카야 범주에 해당한다.

역사

삼각형 범주는 디터 퍼피(1962년)와 장 루이 베르디에(1963년)에 의해 독립적으로 도입되었는데, 비록 퍼피의 공리는 덜 완전했지만(팔면공리(TR 4)를 탈취했다).^[1]Puppee는 안정적인 호모토피 카테고리에 의해 동기부여가 되었다.베르디에의 주요 예는 그가 또한 알렉산더 그로텐디크의 사상을 발전시키면서 정의한 아벨리아 범주의 파생 범주였다.파생 범주의 초기 적용에는 Poincaré 이중성을 단수공간으로 확장하는 일관성 있는 이중성과 Verdier 이중성이 포함되었다.

정의

범주 D의 시프트 또는 변환 펑터는 가법적 자동형성(또는 일부 저자의 경우 자동 등가성) $\Sigma$ 이다 $\Sigma$ .정수 n에 $X[n]=\Sigma ^{n}X$ X $X[n]=\Sigma ^{n}X$ [ $X[n]=\Sigma ^{n}X$ $X[n]=\Sigma ^{n}X$ = $X[n]=\Sigma ^{n}X$ $X[n]=\Sigma ^{n}X$ $X[n]=\Sigma ^{n}X$ 라고 쓰는 것이 일반적이다.

A triangle (X, Y, Z, u, v, w) consists of three objects X, Y, and Z, together with morphisms $u\colon X\to Y$ , $v\colon Y\to Z$ and $w\colon Z\to X[1]$ . Triangles are generally written in the unravelled form:

X{\xrightarrow {{}\at up u}Y{\\xrightarrow {{}\atop v}Z{\xrightarrow {{}\atop w}X[1],

또는

X{\xrightarrow {{}\at up u}Y{\xrightarrow {{}\othop v}Z{\xrightarrow {{}\top w}}}}

요컨대

삼각형 범주는 정확한 삼각형^[2](또는 구별된 삼각형)이라고 불리는 변환 펑터와 삼각형의 클래스가 있는 가법 범주 D이다(TR 1), (TR 2), (TR 3) 및 (TR 4)의 특성을 만족한다(이러한 공리는 다른 것들로부터 파생될 수 있기 때문에 완전히 독립적이지 않다).^[3]

TR 1

모든 개체 X에 대해 다음 삼각형이 정확하다.

X{\overset {\text{id}}{\\to }}X\to 0\to X[1]

모든 형태론 $u\colon X\to Y$ : $u\colon X\to Y$ → Y ${\displaystyle u\colon$ X $\to Y}$ 에 대해 $u\colon X\to Y$ 정확한 삼각형에 맞는 객체 Z(형태론 u의 원뿔 또는 코피버라고 함)가 있다.

X{\\xrightarrow {{}\op u}}}Y\to Z\to X[1]

"코네"라는 이름은 체인 콤플렉스의 지도에 있는 원뿔에서 유래했으며, 이는 위상에서의 지도 콘에서 영감을 얻은 것이다.다른 공리로부터 정확한 삼각형(특히 객체 Z)이 형태론

X\to Y

→

X\to Y

{\

displaystyle X\to Y}

에 의해 이형성까지 결정된다는 것을 알 수 있지만

X\to Y

항상 고유한 이형성까지는 아니다.^[4]

모든 삼각형은 정확한 삼각형과 이형이다.이 말은 만약을 의미한다.

X{\xrightarrow {{}\at up u}Y{\\xrightarrow {{}\atop v}Z{\xrightarrow {{}\atop w}X[1],

정확한 삼각형이며,

f\colon X\to X'

:

f\colon X\to X'

→

f\colon X\to X'

f\colon X\to X'

{\

X

\

to

X

f\colon X\to X'

g\colon Y\to Y'

:

g\colon Y\to Y'

→

g\colon Y\to Y'

g\colon Y\to Y'

{\

h\colon Z\to Z'

:

h\colon Z\to Z'

→

h\colon Z\to Z'

h\colon Z\to Z'

{\

Z

\to

Z

'}

등각형성형성형이다

h\colon Z\to Z'

.

X'{\x오른쪽 화살표 {gf^{-1}Y'{\x오른쪽 화살표 {hvg^{-1}Z'{\x오른쪽 화살표 {f[1]^{-1}X'[1]

또한 정확한 삼각형이다.

TR 2

만약

X{\xrightarrow {{}\at up u}Y{\\xrightarrow {{}\atop v}Z{\xrightarrow {{}\atop w}X[1],

정확한 삼각형이고, 그렇다면 두 개의 회전된 삼각형도 마찬가지다.

Y{\xrightarrow {{}\attop v}Z{\xrightarrow {{}\attop w}X[1]{\xrightarrow {-u[1]}}Y[1]

그리고

Z[-1]{\xrightarrow {-w[-1]}X{\xrightarrow {{}\atop u}Y{\xrightarrow {{}\top v}Z.\

마지막 삼각형을 볼 때, Z[-1] 물체는 $X\to Y$ X → $X\to Y$ ${\displaystyle$ X $\to Y}$ 의 섬유라고 불린다 $X\to Y$

The second rotated triangle has a more complex form when $[1]$ and $[-1]$ are not isomorphisms but only mutually inverse equivalences of categories, since $-w[-1]$ is a morphism from $Z[-1]$ to ${\disp$ $레이스타일 (X[1]][-1]}$ 및 $[X]$ [ $[X]$ $[X]$ $[X]$ 에 대한 형태론을 얻으려면 자연 $[X]$ 변환 $(X[1])[-1]{\xrightarrow {}}X$ [ $(X[1])[-1]{\xrightarrow {}}X$ $(X[1])[-1]{\xrightarrow {}}X$ [ $(X[1])[-1]{\xrightarrow {}}X$ - $(X[1])[-1]{\xrightarrow {}}X$ $(X[1])[-1]{\xrightarrow {}}X$ → $(X[1])[-1]{\xrightarrow {}}X$ ${\displaystyle (X[1])[-1]{\xrightarrow {})$ 로 구성해야 한다 $(X[1])[-1]{\xrightarrow {}}X$ 이것은 자연적 변환에 부과해야 하는공리들에 대한 복잡한 질문으로 이어진다 $[-1]$ [ $1$ $]$ ${\displaystyle [1]$ 및 $[1]$ $[-1]$ [ $[-1]$ - $[-1]$ $[-1]$ ${\displaystyle [-1]}.$ 이 문제로 인해 $,$ [ $1$ $]$ ${\displaystyle [1]$ 과 $[1]$ $[-1]$ [ $[-1]$ - $[-1]$ $[-1]$ $[-1]$ 이(가) 상호 $[-1]$ 역비 이형이라고 가정하는 것이 삼각형 범주의 정의에서 통상적으로 선택하는 선택이다.

TR 3

두 개의 정확한 삼각형과 각 삼각형의 첫 번째 형태 사이의 지도를 보면, 두 삼각형의 세 번째 물체 사이에는 모든 것을 통근하게 만드는 형태론이 존재한다.즉, 다음 다이어그램(두 행이 정확한 삼각형이고 f와 g가 gu = u′f와 같은 형태인 경우)에는 모든 사각형을 통근하는 지도 h(꼭 고유하지는 않음)가 존재한다.

TR 4: 팔면 공리

Let $u\colon X\to Y$ and $v\colon Y\to Z$ be morphisms, and consider the composed morphism $vu\colon X\to Z$ . Form exact triangles for each of these three morphisms according to TR 1. The octahedral axiom states (roughly) that the three mapping cones ca "모든 것이 통근"하도록 정확한 삼각형의 꼭지점으로 만들어진다.

좀 더 형식적으로, 정확한 삼각형이 주어진다.

X{\xrightarrow {u\,}Y{\\xrightarrow {j}Z'{\xrightarrow {k}X[1]

Y{\xrightarrow {v\,}Z{\xrightarrow {l}X'{\xrightarrow {i}}}Y[1]

X{\\xrightarrow {{}\atopvu}Z{\xrightarrow{m}}

Y'{\

x오른쪽

화살표{n}X[1

정확히 삼각형이 있다.

Z'{\xrightarrow{f}Y'{\xrightarrow{g}X'{\xrightarrow {h}Z'[1]

그런

l=gm,\displaystyle k=nf,\dism h=j=j[1]i,\dism ig=u[1]n,\display fj=dism.

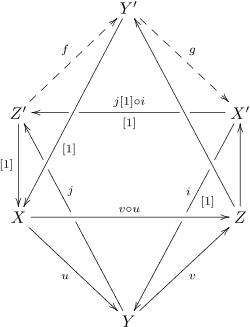
이 공리는 모든 물체와 형태론을 그리면 팔면체의 골격이 생기는데, 그 중 네 개가 정확한 삼각형이기 때문에 "팔면공리"라고 불린다.여기서의 프리젠테이션은 베르디에 자신의 것으로, (Hartshorne 1966)에 8각형 도표로 완성되어 나타난다.다음 도표에서 u와 v는 주어진 형태론이며, 프라이밍된 글자는 다양한 지도(정확한 삼각형마다 X, Y, Z 문자를 갖도록 하기 위한 초선)의 원뿔이다.다양한 화살표는 "1도"임을 나타내기 위해 [1]로 표시되었다. 예를 들어 Z′에서 X까지 지도는 사실 Z′에서 X[1]로 표시된다.그런 다음 팔면 공리는 정확한 삼각형을 형성하는 지도 f와 g의 존재를 주장하여, f와 g가 그것들을 포함하는 다른 면에 역삼각형을 형성한다.

두 개의 다른 그림이 (Beilinson, Bernstein & Deligne 1982년)에 등장한다 (Gelfand와 Manin(2006)도 첫 번째 그림을 제시한다.첫째는 위의 팔면체의 상부 피라미드와 하부 피라미드를 제시하고 하부 피라미드를 부여하면 Y에서 Y로, Y에서 Y로 이어지는 두 경로가 같도록 상부 피라미드를 채울 수 있다고 주장한다(하트쇼른의 발표에서 이 조건은 아마도 잘못되었을 것이다).+로 표시된 삼각형은 대응적이며 "d"로 표시된 삼각형은 정확하다.

두 번째 도표는 좀 더 혁신적인 표현이다.정확한 삼각형은 선형적으로 제시되며, 도표는 "옥타헤드론"에 있는 네 개의 삼각형이 일련의 삼각형 지도에 의해 연결된다는 사실을 강조하는데, 여기에는 세 개의 삼각형(이름, X에서 Y로, Y에서 Z로, 그리고 X에서 Z로 형태화를 완성한 삼각형)이 주어지고 네 번째 삼각형의 존재가 주장된다.하나는 X에 대해 "진행"함으로써 처음 두 개 사이를 지나, 세 번째로는 Z에 대해 선회하며, 네 번째로는 X에 대해 선회한다.이 다이어그램의 모든 엔클로저는 역행(삼각형과 사각형 모두)이지만 Y에서 Y까지의 두 경로의 동일성을 나타내는 다른 역행 사각형은 분명하지 않다."가장자리 바깥"을 가리키는 모든 화살표는 도 1:

또한 이 마지막 도표는 팔면 공리의 유용한 직관적 해석을 보여준다.삼각형 범주에서 삼각형은 정확한 순서의 역할을 하므로, $Z'=Y/X$ 물체를 "정량" $Z'=Y/X$ = "Y $Z'=Y/X$ = $Z'=Y/X$ ${\displaystyle Z'=Y/X},$ $Y'=Z/X$ Y $Y'=Z/X$ = $/X}$ 로 생각하면 암시적이다 $Y'=Z/X$ 그러한 용어로 마지막 $삼각형$ 의 존재는 한 손에 표현된다.

X'=Z/Y\

X'=Z/Y\

= Z

X'=Z/Y\

/

X'=Z/Y\

{\

X

'=

Y\to Z\to X'\to

/Y\

}

X'=Z/Y\

(

Y\to Z\to X'\to

Y →

Y\to Z\to X'\to

Z →

Y\to Z\to X'\to

→ → →

{\displaystyle Y\to X'\to

})

Y\to Z\to X'\to

및

X'=Y'/Z'

X'=Y'/Z'

=

X'=Y'/Z'

X'=Y'/Z'

/

X'=Y'/Z'

X'=Y'/Z'

{\

X

'=Y'/Z'}(

삼각형

Z'\to Y'\to X'\to

Z'\to Y'\to X'\to

→ Y

Z'\to Y'\to X'\to

→

Z'\to Y'\to X'\to

Z'\to Y'\to X'\to

→

Z'\to Y'\to X'\to

"\

displaysty

Z

'\to Y'\to

}).

Z'\to Y'\to X'\to

이를 종합하면, 팔각 공리는 "제3의 이형성 정리"를 주장한다.

[\displaystyle (Z/X)/(Y/X)\cong Z/Y.}

If the triangulated category is the derived category D(A) of an abelian category A, and X, Y, Z are objects of A viewed as complexes concentrated in degree 0, and the maps $X\to Y$ and $Y\to Z$ are monomorphisms in A, then the cones of these morphisms in D(A) are actually isomorphic to the quoA에서 위의 transients.

마지막으로 네만(2001)은 4열과 4열로 이루어진 2차원 정류 도표를 사용하여 팔면 공리를 형성한다.베일린슨, 번스타인, 델린(1982)도 팔면공리를 일반화한다.

특성.

여기 삼각형 범주 D에 대한 공리의 몇 가지 간단한 결과가 있다.

정확한 삼각형 지정

X{\xrightarrow {{}\at up u}Y{\\xrightarrow {{}\atop v}Z{\xrightarrow {{}\atop w}X[1],

D에서, 두 개의 연속적인 형태론의 구성은 0이다.즉, vu = 0, wv = 0, u[1]w = 0 등.^[5]

형태론 $u\colon X\to Y$ : $u\colon X\to Y$ → $u\colon X\to Y$ $u\colon X\to Y$ 을 고려할 때, $u\colon X\to Y$ TR 1은 정확한 삼각형을 완성하는 원뿔 Z의 존재를 보장한다.u의 어떤 두 개의 원뿔도 이형성이지만, 이형성이 항상 독특하게 결정되는 것은 아니다.^[4]

Every monomorphism in D is the inclusion of a direct summand, $X\to X\oplus Y$ , and every epimorphism is a projection $X\oplus Y\to X$ .^[6] A related point is that one should not talk about "injectivity" or "surjectivity" for morphisms in a triangulated category.Every morphism $X\to Y$ that is not an isomorphism has a nonzero "cokernel" Z (meaning that there is an exact triangle $X\to Y\to Z\to X[1]$ ) and also a nonzero "kernel", namely Z[−1].

원추형 구조물의 비기능성

삼각형 범주의 기술적 복잡성 중 하나는 원추형 구조가 functorial이 아니라는 사실이다.예를 들어, $링$ R $R$ 과 $R$ (와) 구분 삼각형 부분 맵이 지정됨

${\begin{matrix}R&\to &0&\to &0&\downarrow &&&\\to &#1]&R[+1]&to \end{matrix}}}$

$D^{b}(R)$ $D^{b}(R)$ ( $D^{b}(R)$ ) $D^{b}(R)$ 에는 $D^{b}(R)$ 이 다이어그램을 완성하는 두 개의 지도가 있다.이것은 신원 지도일 수도 있고 제로 지도일 수도 있다.

${\reasoned}{\text{id}:&R[+1]\to R[+1]\\0:&R[+1]\to R[+1]\end{aigned}}$

둘 다 같은 뜻이야두 개의 지도가 존재한다는 사실은 삼각형 범주가 호모토피 한계와 콜리밋을 암호화하는 도구라는 사실을 보여주는 그림자다.이 문제에 대한 하나의 해결책은 파생 범주뿐만 아니라 이 범주에 대한 다이어그램의 파생 범주를 고려하는 Grotendieck에 의해 제안되었다.그런 물체를 파생기라고 한다.

예

필드 k 위의 벡터 공간은 모든 X에 대해 X[1] = X인 기본 삼각형 범주를 형성한다.정확한 삼각형은 k-선형 지도의 $X\to Y\to Z\to X\to Y$ → $X\to Y\to Z\to X\to Y$ → $X\to Y\to Z\to X\to Y$ → X → $X\to Y\to Z\to X\to Y$ → $X\to Y\to Z\to X\to Y$ → X → X → X → Z $\to$ X $\to Y}$ 시퀀스 X $X\to Y\to Z\to X\to Y$ → $X\to Y$ → Y $[\displaysty$ X $\to Y}$ 이며, X, Y, Z에서 $X\to Y$ → Y}를 두 $X\to Y$ 번 쓴다.
A가 가법 범주(예: $K(A)$ 범주)인 경우, 복합체를 A에 포함하도록 $K(A)$ 호모토피 $K(A)$ K $K(A)$ ( A $K(A)$ ) ${\디스플레이$ 스타일 $K(A)}$ 를 정의하고, 복합체 형태론의 호모토피 클래스를 형태화한다.그러면 $K(A)$ ( $K(A)$ ) $K(A)$ 은 삼각형 범주가 $K(A)$ 된다.^[7]X 시프트[1]는 X가 왼쪽으로 한 단계 이동한 복합체(미분율과 -1을 곱한 값)이다.An exact triangle in $K(A)$ is a triangle which is isomorphic in $K(A)$ to the triangle $X\to Y\to {\text{cone}}(f)\to X[1]$ associated to some map $f\colon X\to Y$ of chain complexes.(여기 ${\text{cone}}(f)$ ( ${\text{cone}}(f)$ ) ${\displaystyle$ {\ $text{cone}(f)}$ 은 체인 맵의 매핑 원뿔을 나타낸다 ${\text{cone}}(f)$ .)
아벨 범주 A의 파생 범주 D(A)는 삼각 범주다.^[8]모든 준 이형성에 대해 국산화하여 단지 C(A)의 범주에서 건설된다.즉, 모든 준 이형성에 대해 공식적으로 역 형태론을 결합한다.D(A)의 대상은 변하지 않는다. 즉, 그것들은 체인 콤플렉스다.An exact triangle in D(A) is a triangle which is isomorphic in D(A) to the triangle $X\to Y\to {\text{cone}}(f)\to X[1]$ associated to some map $f\colon X\to Y$ of chain complexes.
파생 범주의 주요 동기는 A에서 파생된 펑터를 파생 범주의 펑터로 볼 수 있다는 것이다.^[9]Some natural subcategories of D(A) are also triangulated categories, for example the subcategory of complexes X whose cohomology objects $H^{i}(X)$ in A vanish for i sufficiently negative, sufficiently positive, or both, called ${\displaystyle D^{+}(A),$ $D^{-}(A),$ D $^{\text{b}}(A)},$ 각각 $D^{+}(A),D^{-}(A),D^{\text{b}}(A)$
위상에서 안정적 호모토피 범주 $h{\cal {S}}$ ${\$ 는 삼각형 범주다 $h{\cal {S}}$ .^[10]물체는 스펙트럼이고, X[1]는 서스펜션 $\Sigma X$ X ${\displaystyle \Sigma$ X $}($ 또는 동등하게 $\Omega ^{-1}X$ - $\Omega ^{-1}X$ $\Omega ^{-1}X$ ${\displaystyle \Oomega ^{-1}X})$ 이며, $\Omega ^{-1}X$ 정확한 삼각형은 코파이버 시퀀스다.안정적 호모토피 범주(불안정한 호모토피 범주와 비교)의 독특한 특징은 섬유 시퀀스가 코파이버 시퀀스와 동일하다는 점이다.실제로 어떤 삼각형 범주에서도 정확한 삼각형은 섬유 시퀀스로도 볼 수 있고 또한 코파이버 시퀀스로도 볼 수 있다.
유한군 G의 모듈형 표현 이론에서 안정적 모듈 범주 StMod(kG)는 삼각형 범주다.그것의 개체는 필드 k에 대한 G의 표현이며, 형태론은 투영적(또는 동등하게 주입된) kG-module을 통해 인자를 나타내는 일반적인 표현이다.보다 일반적으로, 안정적 모듈 범주는 kG 대신 프로베니우스 대수학에 대해 정의된다.

더 좋은 공리가 있을까?

일부 전문가들은 (예를 들어 (Gelfand & Manin 2006, 소개, 4장 참조) 삼각형 범주가 실제로 "정확한" 개념이 아니라고 의심한다^[11]^{pg 190}.본질적인 이유는 형태론의 원뿔이 비독점 이형성까지만 독특하기 때문이다.특히, 형태론의 원뿔은 일반적으로 형태론에 의존하지 않는다(예를 들어 공리(TR 3)의 비유일성에 주목한다).이러한 고유성이 오류의 잠재적인 원인이다.그러나 이 공리는 실제로도 적절하게 작용하고 있으며, 그들의 연구에 바치는 문헌도 매우 많다.

파생자

대안적인 제안 중 하나는 80년대에^[11]^{pg 191} 그로텐디크가 <추적 스택>에서 제안한 파생자 이론이며, 이후 이 주제에 대한 그의 원고에 90년대에 전개되었다.본질적으로, 이것들은 약한 등가 $(M,W)$ 의 범주에 대해 $I\to M$ 다이어그램 $I\to M$ I $I\to M$ → M → $I\to M$ $displaystyle$ I $\to M}$ 에 의해 주어지는 호모토피 범주들의 시스템이다 $(M,W)$ 이러한 범주들은 $I\to J$ $I\to J$ → $I\to J$ J → J $I\to J$ {\ $displaystyle I\to J}$ 의 형태에 의해 관련된다 $I\to J$ 이 형식주의는 장점을 가지고 있다.f 원뿔 구조를 대체하는 호모토피 한계와 콜리밋을 복구할 수 있다.

안정적인 ∞ 카테고리

또 다른 대안이 구축된 것은 안정적 ∞-categories 이론이다.안정적 ∞-범주의 호모토피 범주는 표준적으로 삼각측량되며, 더욱이 지도용 원뿔은 본질적으로 독특해진다(정확한 호모토피적 의미에서).더욱이 안정된 ∞ 범주는 자연적으로 그것의 호모토피 범주에 대한 호환성의 전체 계층을 암호화하며, 그 아래에는 팔면공리가 있다.따라서 호모토피 범주의 삼각측량 데이터를 제공하는 것보다 안정적 ∞-범주의 데이터를 제공하는 것이 엄격히 더 강하다.실제로 발생하는 거의 모든 삼각형 범주는 안정적인 ∞ 범주에서 나온다.삼각형 범주의 유사한(그러나 더 특별한) 농축은 dg 범주의 개념이다.

어떤 면에서는 삼각형 범주보다 안정적인 ∞ 범주 또는 dg 범주가 더 효과적이다.한 예는 아래에서 설명하는 삼각형 범주 간의 정확한 펑터 개념이다.필드 k에 걸쳐 매끄러운 투영 품종 X의 경우, 일관성 있는 피복의 경계 파생 범주는 ${\text{D}}^{\text{b}}(X)$ ${\text{D}}^{\text{b}}(X)$ ( ${\text{D}}^{\text{b}}(X)$ ) ${\displaystyle {\text{$ $D}^{\text{b}}(X)}$ 은(는) dg-category에서 자연적으로 유래한다 ${\text{D}}^{\text{b}}(X)$ .품종 X와 Y의 경우, X의 dg 범주에서 Y의 범주까지 모든 functor는 푸리에의 $X\times Y$ $X\times Y$ $X\times Y$ ${\displaystyle X\time$ Y $}$ 에 있는 셸의 콤플렉스에서 나온다.무카이 변신.^[12]대조적으로, ${\text{D}}^{\text{b}}(X)$ ${\text{D}}^{\text{b}}(X)$ ( ${\text{D}}^{\text{b}}(X)$ X ) ${\displaystyle$ {\ $text{$ $D}^{\text{b}(X)$ 에서 ${\text{D}}^{\text{b}}(X)$ ${\text{D}}^{\text{b}}(Y)$ ${\text{D}}^{\text{b}}(Y)$ )까지 ${\displaystyle {\text{$ $D}}^{\text{b}}}$ $X\times Y$ $X\times Y$ Y ${\displaystyle$ X $\times$ Y}에 있는 피복 콤플렉스로부터 오는 ${\text{D}}^{\text{b}}(Y)$ 것이 아닌 것 같다 $X\times Y$ ^[13]이 예에서 볼 때 삼각형 범주 간의 형태주의에 대한 "오른쪽" 개념은 기본 dg 범주(또는 안정적 categ-category)의 형태론에서 오는 것으로 보인다.

삼각형 범주보다 안정적인 ∞ 범주 또는 dg 범주의 또 다른 장점은 대수학 K-이론에 나타난다. 이론에 나타난다.정수 i에 대해 $K_{i}(C)$ 일련의 아벨 $K_{i}(C)$ $K_{i}(C)$ $){\displaystyle K_{i}(C)$ 를 부여하면서 안정적인 ∞-카테고리 또는 dg-카테고리 C의 대수 K-이론을 정의할 수 있다. $K_{0}(C)$ K $K_{0}(C)$ ( $K_{0}(C)$ ) $K_{0}(C)$ 은(는) C와 관련된 삼각형 범주에 관한 간단한 설명을 가지고 $K_{0}(C)$ 있다.그러나 dg-카테고리의 K-그룹이 항상 관련 삼각형 범주에 의해 결정되는 것은 아니라는 것을 보여주는 예가 있다.^[14]따라서 삼각형 범주는 K $K_{0}$ ${\$ 그룹이 $K_{0}$ 잘 정의되어 있지만 일반적으로 상위 K 그룹은 아니다.

반면 삼각형 범주의 이론은 안정적 ∞-범주 또는 dg-범주 이론보다 단순하며, 많은 응용에서 삼각형 구조는 충분하다.예를 들면, 삼각 범주 수준에서 많은 연산이 이루어졌고, ∞ 범주나 dg 범주의 추가 구조가 요구되지 않았던 Bloch-Kato 추측의 증거다.

삼각형 범주의 코호몰로지

삼각형 범주는 코호몰로지 개념을 인정하며, 모든 삼각형 범주는 코호몰로지 펑터가 많이 공급된다.삼각형 범주 D에서 아벨 범주 A까지의 코호몰로지 펑터 F는 모든 삼각형에 대해 정확한 펑터다.

(\displaystyle X\to Y\to Z\to X[1],\ }

A에서 $F(X)\to F(Y)\to F(Z)$ $F(X)\to F(Y)\to F(Z)$ ( $F(X)\to F(Y)\to F(Z)$ ) $F(X)\to F(Y)\to F(Z)$ → $F(X)\to F(Y)\to F(Z)$ ( $F(X)\to F(Y)\to F(Z)$ ) $F(X)\to F(Y)\to F(Z)$ → $F(X)\to F(Y)\to F(Z)$ ( Z $F(X)\to F(Y)\to F(Z)$ ) ${\displaystyle$ F $(X)\to F (Y)\to F (Z)}$ 의 순서가 정확하다.정확한 삼각형은 양쪽 방향의 정확한 삼각형의 무한 순서를 결정하므로,

\\displaystyle \cdots \to Z[-1]\to X\to X[1]\cdots ,\}

코호몰로지 펑터 F는 실제로 아벨리아 범주 A:

\\cdots \to F(Z[-1])\to F(X)\to F(Y)\to F(X[1])\to \cdots.\}

A key example is: for each object B in a triangulated category D, the functors $\operatorname {Hom} (B,{\text{-}})$ and $\operatorname {Hom} ({\text{-}},B)$ are cohomological, with values in the category of abelian groups.^[15](정확히 말하면 후자는 역행성 펑터로서 D의 반대 범주에 대한 펑터로서 생각할 수 있다) 즉, 정확한 $X\to Y\to Z\to X[1]$ X $X\to Y\to Z\to X[1]$ → $X\to Y\to Z\to X[1]$ → Z $X\to Y\to Z\to X[1]$ → $X\to Y\to Z\to X[1]$ [ $X\to Y\to Z\to X[1]$ $X\to Y\to Z\to X[1]$ $X\to Z\to X[1]}}$ 는 아벨리아 그룹의 두 가지 긴 정확한 시퀀스를 결정한다 $X\to Y\to Z\to X[1]$ .

\cdots \to \operatorname {Hom}(B,X[i])\to \operatorname {Hom}(B,Z[i])\to \operatorname {Hom}(B,X[i+1)\cdots

그리고

{\displaystyle \cdots \to \operatorname {Hom}(Z,B[i])\to \operatorname {Hom}(Y,B[i])\to \operatorname {Hom}(Z,B[i+1])\to \cdots.}.

특정한 삼각형 범주의 경우, 이러한 정확한 시퀀스는 피복 코호몰로지, 집단 코호몰로지 및 수학의 다른 영역에서 중요한 정확한 시퀀스의 많은 부분을 산출한다.

또한 그 표기법을 사용할 수도 있다.

\operatorname {Ext} ^{i}(B,X)=\operatorname {Hom}(B,X[i])

integers i를 위해, 아벨리아 범주에서 Ext functor를 일반화한다.이 표기법에서는 위의 첫 번째 정확한 순서를 다음과 같이 표기할 것이다.

\cdots \to \operatorname {Ext} ^{i}(B,X)\to \operatorname {Ext} ^{i}(B,Y)\to \operatorname {Ext} ^{i}(B,Z)\to \operatorname {Ext} ^{i+1}(B,X)\to \cdots .\

아벨 범주 A의 경우, 파생 범주 D(A)에 있는 동족 functor의 또 다른 기본 예는 복합 X를 A에 있는 $H^{0}(X)$ $H^{0}(X)$ H $H^{0}(X)$ ( $H^{0}(X)$ ) $H^{0}(X)$ 에 보낸다.즉, D(A)의 $X\to Y\to Z\to X[1]$ 정확한 삼각형 $X\to Y\to Z\to X[1]$ → Y $X\to Y\to Z\to X[1]$ → $X\to Y\to Z\to X[1]$ → X $X\to Y\to Z\to X[1]$ [ $X\to Y\to Z\to X[1]$ $X\to Y\to Z\to X[1]$ {\ $displaystyle$ X $\to Y\to Z\to X[1]}$ 는 A의 긴 정확한 순서를 결정한다.

\cdots \to H^{i}(X)\to H^{i}(Y)\to H^{i}(Z)\to H^{i+1}(X)\cdots ,

$H^{0}(X[i])\cong H^{i}(X)$ $H^{0}(X[i])\cong H^{i}(X)$ ( $H^{0}(X[i])\cong H^{i}(X)$ [ $H^{0}(X[i])\cong H^{i}(X)$ $H^{0}(X[i])\cong H^{i}(X)$ ) $H^{0}(X[i])\cong H^{i}(X)$ H $H^{0}(X[i])\cong H^{i}(X)$ ( $H^{0}(X[i])\cong H^{i}(X)$ ) $H^{0}(X[i])\cong H^{i}(X)$ 을(를) 사용하여 $H^{0}(X[i])\cong H^{i}(X)$ .

정확한 공법 및 동등성

삼각형 범주 D에서 삼각형 범주 E까지 정확한 펑터(삼각형 펑터라고도 함)는 적층 펑터 $F\colon D\to E$ : $F\colon D\to E$ → $F\colon D\to E$ $[\displaystyle F\colon D\to$ E $}$ 이며, 느슨하게 $F\colon D\to E$ 말하면 번역과 통용되어 정확한 삼각형으로 정확한 삼각형을 보낸다.^[16]

In more detail, an exact functor comes with a natural isomorphism $\eta \colon F\Sigma \to \Sigma F$ (where the first $\Sigma$ denotes the translation functor of D and the second $\Sigma$ denotes the translation functor of E), such that whenever

X{\xrightarrow {{}\at up u}Y{\\xrightarrow {{}\atop v}Z{\xrightarrow {{}\atop w}X[1],

D의 정확한 삼각형이고

F(X){\xrightarrow {F(u)}{\xrightarrow {F(v)}{\xrightarrow {\\x}F(w)[1]

E의 정확한 삼각형이다.

삼각형 범주의 등가치는 정확한 functor $F\colon D\to E$ : $F\colon D\to E$ → E $F\colon D\to E$ 이며, 이 또한 $F\colon D\to E$ 범주의 등가물이다.이 경우 FG와 GF가 각각의 ID functor에 자연적으로 이형화되도록 $G\colon E\to D$ 한 $G\colon E\to D$ functor $G\colon E\to D$ : E $G\colon E\to D$ → $G\colon E\to D$ $G\colon E\to D$ 가 있다.

압축적으로 생성된 삼각형 범주

임의 집합(필수적으로 유한하지 않음)에 의해 지수화된 직접 합계가 D에 존재하도록 D를 삼각형 범주로 한다.펑터 홈 D( ${\text{Hom}}_{D}(X,{\text{-}})$ , - ${\text{Hom}}_{D}(X,{\text{-}})$ ) $displaystyle {\text{$ $홈}_{D}(X,{\text$ {-})}은 $($ 는) 직접 합계로 통한다 ${\text{Hom}}_{D}(X,{\text{-}})$ .Explicitly, this means that for every family of objects $Y_{i}$ in D indexed by a set S, the natural homomorphism of abelian groups ${\displaystyle \oplus _{i\in S}\mathrm {Hom} _{D}(X,Y_{i})\to \mathrm {Hom} _{D}(X,\oplus _{i\i$ $n S}Y_{i}}$ 은 $\oplus _{i\in S}\mathrm {Hom} _{D}(X,Y_{i})\to \mathrm {Hom} _{D}(X,\oplus _{i\in S}Y_{i})$ (는) 이형성이다.이것은 범주 이론에서 콤팩트한 물체의 일반적인 개념과는 다르다. 범주 이론에서는 콤팩트한 물체는 단지 결합물만이 아닌 모든 콜리밋을 포함한다.

예를 들어 안정적 호모토피 $h{\cal {S}}$ h $h{\cal {S}}$ ${\$ h ${\cal{S}}$ 에 있는 콤팩트한 물체는 유한 스펙트럼이다 $h{\cal {S}}$ .^[17]반지의 파생 범주에 있는 콤팩트한 물체나, 계획의 준일관적인 파생 범주에 있는 콤팩트한 물체는 완벽한 콤플렉스다.한 분야에 걸쳐 매끄러운 투영 버라이어티 X의 경우, 완벽한 콤플렉스의 Perf(X) 범주는 일관성 있는 셰이브의 경계 유도 범주인 $D_{\text{coh}}^{\text{b}}(X)$ $D_{\text{coh}}^{\text{b}}(X)$ $D_{\text{coh}}^{\text{b}}(X)$ ( $){\displaystyle D_{\coh}^{\$ text ${b$ }}}}{\ $text{b}}(X)$ 로도 볼 수 있다 $D_{\text{coh}}^{\text{b}}(X)$

다음과 같은 경우 삼각형 범주 D가 압축적으로 생성된다.

D에는 임의의(필수적으로 유한할 필요는 없음) 직접 합계가 있다.
D에는 콤팩트 객체의 S가 설정되어 있어 D의 모든 비제로 객체 X에 대해 일부 정수 n에 대해 $Y[n]\to X$ 비제로 맵 $Y[n]\to X$ [ $Y[n]\to X$ $Y[n]\to X$ → $Y[n]\to X$ $[\displaystyle Y[n]\to X}$ 가 있는 S의 객체 Y가 있다.

자연적으로 발생하는 많은 "큰" 삼각형 범주는 다음과 같이 압축적으로 생성된다.

링 R에 대한 모듈의 파생 범주는 하나의 객체인 R-모듈 R에 의해 압축적으로 생성된다.
준법률 준법률적 준법률적 분리형식의 준법률적 파생 범주는 하나의 대상에 의해 압축적으로 생성된다.^[18]
안정적인 호모토피 범주는 하나의 물체인 $S^{0}$ 스펙트럼 $S^{0}$ S 0 {\ $displaystyle$ S^{ $0}$ 에 의해 압축적으로 생성된다 $S^{0}$ ^[19]

Amnon Neeman은 브라운 대표성 정리를 다음과 같이 압축적으로 생성된 삼각형 범주로 일반화했다.^[20]D는 콤팩트하게 생성된 삼각형 범주, $H\colon D^{\text{op}}\to {\text{Ab}}$ : D $H\colon D^{\text{op}}\to {\text{Ab}}$ → $H\colon D^{\text{op}}\to {\text{Ab}}$ ${\$ D $^{\text{op}\to {\text{Ab}}}$ 제품에 $H\colon D^{\text{op}}\to {\text{Ab}}$ 복사물을 가져가는 코호몰로지 펑커(cohomological functor.그렇다면 H는 대표적이다.(즉, $H(X)\cong {\text{Hom}}(X,W)$ ( $H(X)\cong {\text{Hom}}(X,W)$ ) $H(X)\cong {\text{Hom}}(X,W)$ $H(X)\cong {\text{Hom}}(X,W)$ ( $H(X)\cong {\text{Hom}}(X,W)$ , $H(X)\cong {\text{Hom}}(X,W)$ ) ${\displaystyle H(X)\cong {\text{$ $모든$ X에 대해 $H(X)\cong {\text{Hom}}(X,W)$ 홈 $}(X,W)}$ 다른 버전의 경우, D는 압축적으로 생성된 삼각형 범주, T 임의의 삼각형 범주가 되도록 한다.정확한 functor $F\colon D\to T$ : $F\colon D\to T$ → T $F\colon D\to T$ 가 coproducts에 coproducts를 보내면 $F\colon D\to T$ F는 오른쪽 부선을 가진다.

브라운 표현성 정리는 삼각형 범주 사이의 다양한 펑터를 정의하는데 사용될 수 있다.특히 니만은 예외적인 역영상 $displaystyle$ f $^{!]$ 의 구성을 단순화하고 일반화하는 데 그것을 이용했다 $.$ $}}}$ 계획의 형태론 f에 대해 $f^{!}$ , 일관성이 있는 이중성 이론의 중심적 특징.^[21]

t-rays

모든 아벨 범주 A에 대해 파생 범주 D(A)는 완전한 하위 범주(도 0에 집중된 복합체)로 A를 포함하는 삼각 범주다.다른 아벨 범주들은 동등한 파생 범주를 가질 수 있기 때문에, D(A)에서 A를 삼각형 범주로 재구성하는 것이 항상 가능하지는 않다.

알렉산더 빌린슨, 조셉 번스타인, 피에르 들랭은 이 상황을 삼각형 범주 D의 t-구조 개념으로 설명했다.^[22]D의 t 구조물은 D 내부의 아벨리아 범주를 결정하며, D의 다른 t 구조물은 다른 아벨리아 범주를 산출할 수 있다.

로컬라이징 및 씩 하위 카테고리

D를 임의의 직접 합계가 있는 삼각형 범주로 하자.D의 국지화 하위 범주는 임의의 직접 합계로 마감되는 엄격히 완전한 삼각형 하위 범주다.^[23]:만약 간결하게 생성된 곳에서 삼각형을 이루카테고리 D의 국산화 하위 범주 S개체의 집합,에 의해 발생된 다음 커널 S.[24](그것은 갖고 있는 정확한 삼각형 Y→ X→ 나는 X→ Y[1]{\displaysty의 대상은 모두 XD에서 Bousfield 국산화 함수 기호 L:D→ D{L\colon D\to D\displaystyle}의 이름을 설명하기 위해.르 $예$ 를 들어, 이 구조는 Y가 S에 있고 Y가 오른쪽 직교 $⊥{\$ S $^{\perp }}}$ 에 있는 Y가 있는 X $\to LX\to Y[1]}$ 을(를) 사용하여 $Y\to X\to LX\to Y[1]$ 프라임 번호에서 스펙트럼의 국산화 또는 공간의 피복 콤플렉스에서 열린 부분 집합으로의 제약을 포함한다.

병렬 개념은 "작은" 삼각형 범주에 더 적합하다: 삼각형 범주 C의 두꺼운 하위 범주는 직접 산술에 따라 닫히는 완전 삼각형 하위 범주다. (C가 idempotent-완전한 경우, 하위 범주는 idempotent-완전한 경우에만 두껍다.지역화 하위 카테고리는 두껍다.^[25]따라서 S가 삼각형 범주 D의 국소화 하위 범주라면, S와 콤팩트 개체의 하위 $D^{\text{c}}$ $D^{\text{c}}$ $D^{\text{c}}$ c ${\$ D $^{\text{c}}$ 의 교차점은 $D^{\text{c}}$ c ${\$ D $^{\c}$ 의 두꺼운 하위 범주인 것이다 $D^{\text{c}}$

예를 들어, 데비나츠–Hopkins-Smith는 유한 스펙트럼의 삼각형 범주의 모든 두꺼운 하위 범주를 Morava K-이론 관점에서 설명했다.^[26]안정적 호모토피 범주의 국산화 하위 범주는 분류되지 않았다.

참고 항목

메모들

^ 퍼피(1962년, 1967년), 베르디에(1963년, 1967년).
^ Weibel(1994), Definition 10.2.1.
^ J. 피터 메이, 삼각형 범주에 대한 공리.
^ ^a ^b Weibel(1994), 주석 10.2.2.
^ Weibel(1994), 연습 10.2.1.
^ Gelfand & Manin(2006), 연습 IV.1.1.
^ 가시와라 & 샤피라(2006)정리 11.2.6.
^ Weibel(1994), Corollary 10.4.3.
^ Weibel(1994), 섹션 10.5.
^ Weibel(1994), 정리 10.9.18.
^ ^a ^b Grothendieck. "Pursuing Stacks". thescrivener.github.io. Archived (PDF) from the original on 30 Jul 2020. Retrieved 2020-09-17.
^ 토엔(2007년), 정리 8.15.
^ 리자르도 외(2019), 정리 1.4.
^ Dugger & Shipley (2009년), Remark 4.9.
^ Weibel(1994), 사례 10.2.8.
^ Weibel(1994), Definition 10.2.6.
^ Neeman(2001), Remark D.1.5.
^ Stacks Project, Tag 09IS, Stacks Project, Tag 09M1.
^ Neeman(2001), Leemma D.1.3.
^ Neeman(1996), 이론 3.1 및 4.1.
^ Neman(1996), 예 4.2.
^ 베일린슨 외 연구진(1982), 정의 1.3.1.
^ Neeman(2001), 소개, 1.4 이후.
^ 크라우스(2010), 정리, 소개.
^ Neeman(2001), Remark 3.2.7.
^ 라베넬(1992년), 정리 3.4.3.

참조

삼각형 범주에 대한 일부 교과서 소개는 다음과 같다.

Gelfand, Sergei; Manin, Yuri (2006), "IV. Triangulated Categories", Methods of homological algebra, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, doi:10.1007/978-3-662-12492-5, ISBN 978-3540435839, MR 1950475
Kashiwara, Masaki; Schapira, Pierre (2006), Categories and sheaves, Grundlehren der mathematischen Wissenschaften, Berlin, New York: Springer-Verlag, doi:10.1007/3-540-27950-4, ISBN 978-3-540-27949-5, MR 2182076
Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.

응용 프로그램에 대한 간략한 요약은 다음과 같다.

Kashiwara, Masaki; Schapira, Pierre (2002), "Chapter I. Homological Algebra", Sheaves on manifolds, Grundlehren der mathematischen Wissenschaften, Springer-Verlag, doi:10.1007/978-3-662-02661-8, ISBN 978-3540518617, MR 1074006

일부 고급 참고문헌은 다음과 같다.

Beilinson, A.A.; Bernstein, J.; Deligne, P. (2018) [1982], "Faisceaux pervers", Astérisque, Société Mathématique de France, Paris, 100, ISBN 978-2-85629-878-7, MR 0751966
Dugger, Daniel; Shipley, Brooke (2009), "A curious example of triangulated-equivalent model categories which are not Quillen equivalent", Algebraic and Geometric Topology, 9: 135–166, arXiv:0710.3070, doi:10.2140/agt.2009.9.135, MR 2482071
Hartshorne, Robin (1966), "Chapter I. The Derived Category", Residues and duality, Lecture Notes in Mathematics 20, Springer-Verlag, pp. 20–48, doi:10.1007/BFb0080482, ISBN 978-3-540-03603-6, MR 0222093
Krause, Henning (2010), "Localization theory for triangulated categories", Triangulated categories, London Mathematical Society Lecture Note Series, vol. 375, Cambridge University Press, pp. 161–235, arXiv:0806.1324, doi:10.1017/CBO9781139107075.005, MR 2681709
Neeman, Amnon (1996), "The Grothendieck duality theorem via Bousfield's techniques and Brown representability", Journal of the American Mathematical Society, 9: 205–236, doi:10.1090/S0894-0347-96-00174-9, MR 1308405
Neeman, Amnon (2001), Triangulated categories, Annals of Mathematics Studies, Princeton University Press, doi:10.1515/9781400837212, ISBN 978-0691086866, MR 1812507
Puppe, Dieter (1962), "On the formal structure of stable homotopy theory", Colloquium on algebraic topology, Aarhus Universitet Matematisk Institute, pp. 65–71, Zbl 0139.41106
Puppe, Dieter (1967), "Stabile Homotopietheorie. I.", Mathematische Annalen, 169: 243–274, doi:10.1007/BF01362348, MR 0211400
Ravenel, Douglas (1992), Nilpotence and periodicity in stable homotopy theory, Princeton University Press, ISBN 9780691025728, MR 1192553
Rizzardo, Alice; Van den Bergh, Michel; Neeman, Amnon (2019), "An example of a non-Fourier-Mukai functor between derived categories of coherent sheaves", Inventiones Mathematicae, 216: 927–1004, arXiv:1410.4039, doi:10.1007/s00222-019-00862-9, MR 3955712
Toën, Bertrand (2007), "The homotopy theory of dg-categories and derived Morita theory", Inventiones Mathematicae, 167: 615–667, arXiv:math/0408337, doi:10.1007/s00222-006-0025-y, MR 2276263
Verdier, Jean-Louis (1977) [1963], "Catégories dérivées: quelques résultats (état 0)", Cohomologie étale (SGA 4 1/2) (PDF), Lecture Notes in Mathematics, vol. 569, Springer, pp. 262–311, doi:10.1007/BFb0091525, ISBN 978-3-540-08066-4, MR 3727440
Verdier, Jean-Louis (1996) [1967], Des catégories dérivées des catégories abéliennes, Astérisque, vol. 239, Société Mathématique de France, MR 1453167

외부 링크

J. 피터 메이, 삼각형 범주에 대한 공리
The Stacks Project Authors, The Stacks Project

[1] 퍼피(1962년, 1967년), 베르디에(1963년, 1967년).

[2] Weibel(1994), Definition 10.2.1.

[3] J. 피터 메이, 삼각형 범주에 대한 공리.

[cone-4] Weibel(1994), 주석 10.2.2.

[5] Weibel(1994), 연습 10.2.1.

[6] Gelfand & Manin(2006), 연습 IV.1.1.

[7] 가시와라 & 샤피라(2006)정리 11.2.6.

[8] Weibel(1994), Corollary 10.4.3.

[9] Weibel(1994), 섹션 10.5.

[10] Weibel(1994), 정리 10.9.18.

[:0-11] Grothendieck. "Pursuing Stacks". thescrivener.github.io. Archived (PDF) from the original on 30 Jul 2020. Retrieved 2020-09-17.

[12] 토엔(2007년), 정리 8.15.

[13] 리자르도 외(2019), 정리 1.4.

[14] Dugger & Shipley (2009년), Remark 4.9.

[15] Weibel(1994), 사례 10.2.8.

[16] Weibel(1994), Definition 10.2.6.

[17] Neeman(2001), Remark D.1.5.

[18] Stacks Project, Tag 09IS, Stacks Project, Tag 09M1.

[19] Neeman(2001), Leemma D.1.3.

[grduality-20] Neeman(1996), 이론 3.1 및 4.1.

[21] Neman(1996), 예 4.2.

[22] 베일린슨 외 연구진(1982), 정의 1.3.1.

[23] Neeman(2001), 소개, 1.4 이후.

[24] 크라우스(2010), 정리, 소개.

[25] Neeman(2001), Remark 3.2.7.

[26] 라베넬(1992년), 정리 3.4.3.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[25]

[26]

Search