벡터 번들

뫼비우스 스트립은 1-sphereS¹ 위에 있는 선다발이다. 국소적으로 S의¹ 모든 지점을 중심으로 U × R(여기서 U는 점을 포함한 열린 호)처럼 보이지만, 전체 번들은 S¹ × R(대신 원통형)과는 다르다.

수학에서 벡터다발은 다른 공간 X에 의해 매개변수화된 벡터 공간 계열의 아이디어를 정밀하게 만드는 위상학적 구조(예를 들어 X는 위상학적 공간, 다지관 또는 대수적 다양성이 될 수 있다): 우리가 연관시킨 공간 X의 모든 지점에 대해(또는 "첨부") 이러한 벡터 스페이크 방식으로 벡터 공간 V(x)를 정밀하게 만드는 위상학적 구조다.es는 X와 같은 종류의 또 다른 공간(예: 위상학적 공간, 다지관 또는 대수적 다양성)을 형성하기 위해 함께 적합하며, 이를 X 위에 벡터 번들이라고 한다.

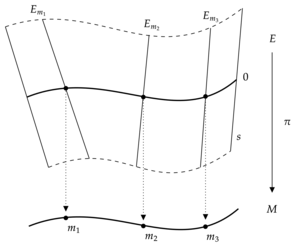
가장 간단한 예는 벡터 공간의 패밀리가 일정한 경우, 즉 V(x) = X의 모든 X에 대해 V: 이 경우 X의 각 X에 대해 V의 복사본이 있고 이 복사본들이 X의 벡터 번들 X x V를 형성하기 위해 함께 적합되는 고정 벡터 공간 V가 있는 경우다. 그러한 벡터 번들은 사소한 것이라고 한다. 더 복잡한 (그리고 프로토타입적인) 예로는 매끄러운 (또는 다른) 다지관의 접선 다발이다. 그러한 다지관의 모든 지점에 접선 공간을 그 지점에서 다지관에 부착한다. 접선다발은 일반적으로 사소한 묶음이 아니다. 예를 들어 구의 접선다발은 털이 많은 공의 정리로는 비교가 안 된다. 일반적으로 다지관의 접선다발이 사소한 것일 경우에만 평행할 수 있다고 한다.

그러나 벡터 번들은 거의 항상 지역적으로 사소한 것이 요구되는데, 이것은 그것들이 섬유 번들의 예라는 것을 의미한다. 또한 벡터 공간은 대개 실제 또는 복잡한 숫자에 걸쳐 있어야 하는데, 이 경우 벡터 번들은 실제 또는 복잡한 벡터 번들(존중적으로)이라고 한다. 복잡한 벡터 번들은 구조가 추가된 실제 벡터 번들로 볼 수 있다. 다음에서는 위상학적 공간의 범주에 있는 실제 벡터 번들에 초점을 맞춘다.

정의와 첫 번째 결과

기본

M

M

위에

E

있는 벡터

번들

E

{\displaystyle

E

M

M

M

의

m_{1}

포인트

E_{m_{1}}

m_{1}

m_{1}

{\

에 해당하는

M

벡터 번들

E

{\displaystystyle E}

의 파이버

E_{m_{1}}

E

1}에 해당하는 파이버가

m_{1}

로 매핑된다.

m_{1}

\pi :E\to M

by

m_{1}

: E

\pi :E\to M

→

\pi :E\to M

{\

displaystyle

\pi

:

E\to

M

\pi :E\to M

실제 벡터 번들은 다음과 같이 구성된다.

위상 공간 X(기본 공간) 및 E(총 공간)
연속추출 π : E → X (번들 투영)
X의 모든 X에 대해, 섬유상의 유한 차원 실제 벡터 공간의 구조 $π$ ⁻¹({x})

다음과 같은 호환성 조건이 충족되는 경우: X의 모든 포인트 P에 대해 오픈근린 U ⊆ X of p, 자연수 k, 동형성이 있다.

\varphi \colon U\times \mathbf {R} ^{k}\to \pi ^{-1}(U)

그래서 모든 X ∈ U에 대해서

$(\pi \circ \varphi )(x,v)=x$ ( $(\pi \circ \varphi )(x,v)=x$ $(\pi \circ \varphi )(x,v)=x$ ) $(\pi \circ \varphi )(x,v)=x$ ( $(\pi \circ \varphi )(x,v)=x$ , v $(\pi \circ \varphi )(x,v)=x$ ) = ${\displaystyle (\pi \circirc \varphi )(x,v)=x},$ 그리고 R의^k 모든 벡터 v에 대해 $(\pi \circ \varphi )(x,v)=x$
지도 $v\mapsto \varphi (x,v)$ $v\mapsto \varphi (x,v)$ ( $v\mapsto \varphi (x,v)$ , $v\mapsto \varphi (x,v)$ $){\displaystyle v\mapsto \varphi (x,v)}$ 는 $v\mapsto \varphi (x,v)$ 벡터 공간 R과^k $π$ ⁻¹({x}) 사이의 선형 이형성이다.

개방적인 근린 U와 동형성 $\varphi$ $\varphi$ 을 $\varphi$ (를) 함께 벡터 번들의 지역적 사소한 것으로 부른다. 국소적인 사소한 부분화는 현지 지도 $π$ U × R의^k U × R의 투영법을 "모양"하고 있음을 보여준다.

모든 섬유 $π$ ⁻¹({x})은 유한 차원 실제 벡터 공간이며, 따라서 차원_x k가 있다. 국소소소요법은 함수 x ↦ k가_x 국소적으로 일정하며, 따라서 X의 연결된 각 구성 요소에서 일정하다는 것을 보여준다. 만약_x k가 모든 X에서 상수 k와 같다면, k는 벡터다발의 등급이라고 하며, E는 순위 k의 벡터다발이라고 한다. 종종 벡터 번들의 정의는 등급이 잘 정의되어 있어서 k가_x 일정하다는 것을 포함한다. 순위 1의 벡터 번들을 라인 번들이라고 하는데 반해, 순위 2의 벡터 번들은 일반적으로 평면 번들이라고 덜 불린다.

투영 X × R^k → X가 장착된 데카르트 제품 X × R은^k X 위에 있는 k등급의 사소한 묶음이라고 불린다.

전환 함수

Two trivial vector bundles over open sets

U_{\alpha }

and

U_{\beta }

may be glued over the intersection

U_{\alpha \beta }

by transition functions

g_{\alpha \beta }

which serve to stick the shaded grey regions together 섬유에 선형 변환을 적용한 후(

g_{\alpha \beta }

g_{\alpha \beta }

g_{\alpha \beta }

{\

\beta \

beta

\ \

}

의 영향으로 파란색 사각형의 변환에 주목한다.)

g_{\alpha \beta }

전환 기능의 서로 다른 선택은 접착이 완료된 후 서로 다른 벡터 번들을 야기할 수 있다.

뫼비우스 스트립은 원¹ S의 오픈 서브셋 U와 V에 두 개의 사소한 묶음을 비종교적으로 붙여서 만들 수 있다. 사소한 것(g_UV=1)으로 접착하면 사소한 보따리를 얻게 되지만, 하나의 겹침에는_UV g=1이, 두 번째 겹침에는 g_UV=-1이 아닌 보따리 E가 붙으면 뫼비우스 띠가 붙는다. 이는 로컬 차트 중 하나의 "트위팅"으로 시각화할 수 있다.

벡터 번들 E → X 등급 k, 그리고 한 쌍의 이웃 U 및 V를 부여하여 번들이 다음을 통해 사소한 것으로 간주함

{\begin{aligned}\varphi _{U}\colon U\times \mathbf {R} ^{k}&\mathrel {\xrightarrow {\cong } } \pi ^{-1}(U),\\\varphi _{V}\colon V\times \mathbf {R} ^{k}&\mathrel {\xrightarrow {\cong } } \pi ^{-1}(V)\end{aligned}}

복합 함수

\varphi _{U}^{-1}\circle \varphi _{V}\colon (U\cap V)\time \mathbf {R}\to (U\cap V)\time \mathbf {R}{R} ^{k}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}

겹치는 부분이 잘 정의되어 있으며, 충족됨

\varphi _{U}^{-1}\circle \varphi _{V}(x,v)=\left(x,g_{UV}(x)v\right)}}

일부 GL(k) 값 함수의 경우

g_{UV}\colon U\cap V\to \operatorname {GL}(k)

이를 벡터 번들의 전이 함수(또는 좌표 변환)라고 한다.

전환 기능 세트는 다음과 같은 의미에서 체치 코키클을 형성한다.

g_{UU}(x)=I,\quad g_{UV}(x)g_{VW}(x)g_{WU}(x)=I

for all U, V, W over which the bundle trivializes satisfying $U\cap V\cap W\neq \emptyset$ . Thus the data (E, X, $π$ , R^k) defines a fiber bundle; the additional data of the g_UV specifies a GL(k) structure group in which the action on the fiber is the standard action of GL(k).

반대로, 섬유^k R에 GL(k) cocycle이 표준적인 방식으로 작용하는 섬유다발(E, $X$ , ,, R^k)이 주어지면 벡터다발이 연관된다. 벡터 번들에 대한 섬유 번들 구성 정리의 예로서 벡터 번들의 대체 정의로 삼을 수 있다.

서브번들

1차원 다지관

M

M

위에

E

있는 사소한 순위 2 벡터 번들

E

E

의

L

선 하위

분절

L

{\displaystyle L

M

벡터 번들을 구성하는 한 가지 간단한 방법은 다른 벡터 번들의 하위 번들을 취하는 것이다. 벡터 번들 $\pi :E\to X$ : $\pi :E\to X$ → $\pi :E\to X$ ${\displaystyle \pi$ :위상학적 공간 위에 $\pi :E\to X$ $있는$ E\ $to$ X $}$ 하위 분개는 단순히 $F\subset E$ ⊂ $F\subset E$ $F\subset E$ 의 하위 공간이며, 제한 restriction $F\subset E$ $\left.\pi \right|_{F}$ ${\$ \ $pi \right _{F}$ 에서 $\left.\pi \right|_{F}$ $\pi$ F $F$ 까지 $\pi$ $\$ pi \{F}가 $F$ $\left.\pi \right|_{F}:F\to X$ : $\left.\pi \right|_{F}:F\to X$ → X ${\displaystyle \왼쪽$ 을 부여한다 $.$ $\pi \right _{F}:$ $벡터 번들의 구조$ 도 F\to $\left.\pi \right|_{F}:F\to X$ X $}.$ 이 경우 섬유 $F_{x}\subset E_{x}$ $F_{x}\subset E_{x}$ $F_{x}\subset E_{x}$ $F_{x}\subset E_{x}$ $F_{x}\subset E_{x}$ ${\$ 는 모든 $x\in X$ $x\in X$ $x\in X$ ${\displaystyle$ x $\in$ X $}$ 에 대한 벡터 하위 공간이다 $F_{x}\subset E_{x}$ $x\in X$

사소한 번들의 하위 번들은 사소한 것이 될 필요가 없으며, 실제로 모든 실제 벡터 번들은 충분히 높은 계급의 사소한 번들의 하위 번들로 볼 수 있다. 예를 들어 원을 넘는 비종교 선다발인 뫼비우스 밴드는 원을 넘는 사소한 2등 다발의 하위 번들로 볼 수 있다.

벡터 번들 형태론

벡터 번들 $π$ ₁: E₁ → X에서₁ 벡터 번들 $π$ ₂: E₂ → X까지의₂ 형태론은 다음과 같은 두 쌍의 연속 지도 f: E₁ → E₂ 및 g: X → X에₁₂ 의해 주어진다.

g₁ ∘ = =

π

₂ f

X의₁ 모든 X에 대해 f가 유도하는 지도

π

₁⁻¹({x}) → →(

x

₂⁻¹)}은 벡터 공간 사이의 선형 지도다.

g는 f에 의해 결정되며(왜냐하면 $π$ 은₁ 허탈하기 때문이다), f는 g를 덮는다고 한다.

모든 벡터 번들의 클래스와 번들 형태는 범주를 형성한다. 공간이 다지관인 벡터 번들(그리고 번들 투영은 매끄러운 지도)과 매끄러운 번들 형태화로 제한하면 매끄러운 벡터 번들의 범주를 얻을 수 있다. 벡터 번들 형태론은 섬유 번들 사이의 번들 맵 개념의 특별한 경우로서 종종 (벡터) 번들 동형체라고도 불린다.

E에서₁ E로₂ 묶음 동형성(E에서₂ E로₁)이라고도 하는 역형성(Bundle homorphism)이 있는 묶음 동형성을 (벡터) 묶음 이형성이라고 하고, 그 다음에 E와₁ E는₂ 이형 벡터 묶음이라고 한다. X보다 작은 묶음(X보다 작은 k위)과 함께 X보다 (k위) 벡터 번들 E의 이소형성을 E의 사소한 묶음(또는 시시콜콜한)이라고 하며, E는 그 다음에 사소함(또는 시시콜콜콜콜한)이라고 한다. 벡터 번들의 정의는 어떤 벡터 번들이 로컬로 하찮은 것임을 보여준다.

고정된 기본 공간 X에 대한 모든 벡터 번들의 범주도 고려할 수 있다. 이 범주의 형태론으로서 우리는 기본 공간에 있는 지도가 X에 있는 ID 맵인 벡터 번들의 형태론을 취한다. 즉, 다음 도표가 통용되는 번들 형태론이다.

(이 범주는 아벨리안이 아니며, 벡터 번들의 형태론의 알맹이는 일반적으로 어떤 자연적인 방법으로도 벡터 번들이 아니다.)

벡터 번들 $π$ ₁: E₁ → X와₁ π₂₂: E₂ → X의₂ 지도 g를 커버하는₁ E → X 사이의 벡터 번들 형태론도 E에서 풀백₁ 번들 g*E까지의₂ X에₁ 대한 벡터 번들 형태론이라고 볼 수 있다.

섹션 및 로컬 무료 셰이브

섹션

s

가

s

인

M

기본

M

M

위에

E

있는 벡터

번들

E

{\displaystyle E

s

표면의 각 점에 정상과 연관된 지도를 하나의 섹션으로 생각할 수 있다. 표면은 공간 X이며, 각 지점 x에는 x에 부착된 벡터 공간에 벡터가 있다.

Given a vector bundle $π$ : E → X and an open subset U of X, we can consider sections of $π$ on U, i.e. continuous functions s: U → E where the composite $π$ ∘ s is such that ( $π$ ∘ s)(u) = u for all u in U. Essentially, a section assigns to every point of U a vector from the attached vector space, in a continuous manner. 예를 들어, 차동 다지관의 접선 다발의 섹션은 그 다지관의 벡터장일 뿐이다.

F(U)를 U.F(U)의 모든 섹션의 집합으로 하자. F(U)는 항상 적어도 하나의 요소, 즉 0 섹션: U의 모든 요소를 벡터 공간 $π$ ⁻¹({x})의 0 요소에 매핑하는 함수 s를 포함한다. 단면들의 점적 덧셈과 스칼라 곱셈으로 F(U)는 그 자체로 진짜 벡터 공간이 된다. 이러한 벡터 공간의 집합은 X에 있는 벡터 공간의 집합이다.

s가 F(U)의 원소이고 α: U → R이 연속 지도라면 α(점괘 스칼라 곱셈)는 F(U)에 있다. 우리는 F(U)가 U에서 연속적인 실질 가치 함수의 링 위에 있는 모듈임을 안다. 더욱이 O가_X X에서 연속적인 실질 가치 함수의 구조 층을 나타낸다면 F는 O-modules의_X 층이 된다.

모든 O-modules가_X 벡터 묶음에서 발생하는 것은 아니다: 국소적으로 자유로운 것만이 그렇다. (이유: 국소적으로 우리는 투영 U × R → U의 섹션을 찾고 있다; 이것들은 정확히 연속함수 U → R이고^k, 그러한 함수는 연속함수 U → R의^k k-tuple이다.)

더욱이 X 상의 실제 벡터 번들의 범주는 국소적으로 자유롭고 미세하게 생성된_X O-module의 범주와 동일하다.

그래서 우리는 X에 있는 실제 벡터 번들의 범주를 O-module의_X 범주 안에 있는 것으로 생각할 수 있다; 이 후자의 범주는 아벨리안이다. 그래서 여기서 우리는 벡터 번들의 형태론의 커널과 코커넬을 계산할 수 있다.

순위 n 벡터 번들은 만약 그것이 선형적으로 독립된 글로벌 섹션을 가지고 있다면 사소한 것이다.

벡터 번들에 대한 작업

벡터 공간에 대한 대부분의 연산은 벡터 공간 연산을 섬유로 수행하여 벡터 번들로 확장할 수 있다.

예를 들어, E가 X에 대한 벡터 번들이라면 X에 대한 번들 E*가 있는데, 이중 번들이라고 하는 것이 있는데, X에 있는 섬유는 이중 벡터 공간(E_x)*이다. 형식적으로 E*는 쌍들의 집합(x, φ)으로 정의할 수 있는데, 여기서 x ∈ X와 φ ∈ (E_x)*는 x ∈ X의 집합으로 정의할 수 있다. 이중다발은 E의 국소적 소소함 역행의 이중공간이 E*의 국소적 소소함이기 때문에 국소적으로 사소한 것이다: 여기서 핵심은 이중 벡터 공간을 차지하는 연산이 functorial이라는 것이다.

벡터 공간 쌍(동일한 영역에 걸쳐)에서 수행될 수 있는 많은 플렉토리얼 연산이 있으며, 이는 벡터 번들 E, F on X(주어진 필드에 걸쳐) 쌍으로 직접 확장된다. 몇 가지 예가 뒤따른다.

Whitney sum (Hassler Whitney의 이름) 또는 E와 F의 직접 sum bund는 벡터 번들 E over F over X의 섬유는 벡터 공간 E와_x F의 직접_x sum E_x ⊕ F이다_x.
텐서 제품 번들 E ⊗ F는 벡터 공간의 섬유질 텐서 제품을 사용하여 유사한 방식으로 정의된다.
Hom-bundle Hom(E, F)은 x에 있는 섬유질이_x E에서_x F까지의 선형 지도의 공간(Hom(E_x_x, F) 또는 L_x(E_x, F)로 표기되는 경우가 많다)인 벡터 번들이다. Hom-bundle은 X에 대한 E에서 F까지의 벡터 번들 동형식과 X에 대한 Hom(E, F)의 섹션 사이에 편차가 있기 때문에 (그리고 유용하다)라고 불린다.
앞의 예에 의거하여, 내형성 번들 Hom(E, E)과 함수 f: X → R의 단면 s에 의거하여, 선형 지도 s(x)의 f(x)-Eigenspace가 되는 지점 x ∈ X 위로 광섬유를 가져가서 고유번들을 구성할 수 있다. E_x → E_x. 이 구조는 자연스럽지만 주의를 기울이지 않는 한 결과물에는 국부적인 사소한 것이 없다. s가 0 구역이고 0이 분리된 f의 경우를 생각해 보십시오. 결과적인 "유겐분들"에서 이러한 영점 위에 있는 섬유는 E에서 그 위에 있는 섬유에 이형성이 될 것이고, 반면에 그 밖의 모든 곳에서는 섬유는 사소한 0차원 벡터 공간이다.
이중 벡터 번들 E*는 E의 번들 동형성의 홈 번들 Hom(E, R × X)과 사소한 번들 R × X이다. 표준 벡터 번들 이형성 Hom(E, F) = E* ⊗ F가 있다.

이러한 각각의 연산은 번들의 일반적인 특징의 특별한 예로서 벡터 공간의 범주에서 수행될 수 있는 많은 연산을 또한 재미있는 방식으로 벡터 번들의 범주에서 수행할 수 있다. 이것은 매끄러운 functor의 언어로 정밀하게 만들어졌다. 다른 성격의 수술은 풀백 묶음 건설이다. 벡터 번들 E → Y와 연속 지도 f: X → Y가 주어지면 X 위에 있는 벡터 번들 f*E에 E를 "뒤로 당길" 수 있다. 점 x × X 위의 섬유는 본질적으로 f(x) ∈ Y 위에 있는 섬유일 뿐이다. 따라서 휘트니의 합계 E ⊕ F는 X에서 X × X까지 대각선 지도의 풀백 번들로 정의할 수 있다. 여기서 X × X 위에 있는 묶음은 E × F이다.

비고: X를 콤팩트한 공간으로 두자. X 위에 있는 벡터 번들 E는 사소한 번들의 직접적인 요약이다. 즉, E ⊕ E'가 사소한 것이 되는 번들 E'가 존재한다. 예를 들어, 무한 실제 투영 공간 위에 있는 tautological line bundle에는 이 속성이 없는 경우 X가 압축되지 않으면 이 오류가 발생한다.^[1]

추가 구조 및 일반화

벡터 번들은 종종 더 많은 구조가 주어진다. 예를 들어 벡터 번들에는 벡터 번들 메트릭이 장착될 수 있다. 일반적으로 이 측정기준은 양적으로 명확한 것이 요구되며, 이 경우 E의 각 섬유는 유클리드 공간이 된다. 복잡한 구조를 가진 벡터 번들은 복잡한 벡터 번들에 해당하는데, 이는 또한 정의의 실제 벡터 공간을 복잡한 것으로 대체하고 모든 매핑을 섬유에서 복합 선형으로 요구함으로써 얻을 수도 있다. 좀 더 일반적으로, 사람들은 일반적으로 벡터 번들에 부과되는 추가적인 구조를 번들의 구조 그룹의 결과적인 감소 측면에서 이해할 수 있다. 보다 일반적인 위상학 분야에 걸친 벡터 번들도 사용될 수 있다.

유한 차원 벡터 공간 대신 섬유 F를 바나흐 공간으로 가져간다면 바나흐 번들을 얻는다.^[2] 구체적으로는 각 섬유에 대한 Barnach 공간 이형성(선형 이형성만이 아닌)과 더 나아가 전이를 요구해야 한다.

g_{UV}\colon U\cap V\to \operatorname {GL}(F)

Banach 다지관의 연속적인 매핑이다. C^p 번들에 대한 해당 이론에서, 모든 매핑은^p C가 되어야 한다.

벡터 번들은 특별한 섬유 묶음이며, 섬유는 벡터 공간이고, 코키클은 벡터 공간 구조를 존중한다. 더 일반적인 섬유 묶음은 섬유에 다른 구조가 있을 수 있는 형태로 구성될 수 있다. 예를 들어 구체 묶음은 구에 의해 섬유화된다.

부드러운 벡터 번들

벡터 번들을 기술하는 전환 함수의 규칙성은 벡터 번들의 유형을 결정한다. 연속 전이 함수 g를_UV 사용할 경우 결과 벡터 번들 E는 연속적일 뿐 매끄럽지 않다. 매끄러운 전환 함수 h를_UV 사용할 경우, 결과 벡터 번들 F는 매끄러운 벡터 번들이다.

벡터 번들(E, p, M)은 매끄러우며, E와 M이 매끄러운 다지관이라면 p: E → M은 매끄러운 지도이며, 국소소소사화는 차이점형이다. 필요한 부드러움의 정도에 따라 C다발^p, 무한히 다른 C 번들^∞, 그리고 실제 분석 C 번들^ω 등 그에 상응하는 개념이 다르다. 이 섹션에서는 C번들에^∞ 초점을 맞출 것이다. C-벡터^∞ 번들의 가장 중요한 예는 C-매니폴드^∞ M의 접선 번들(TM, $π$ _TM, M)이다.

매끄러운 벡터 번들은 사소한 차트 U와 V의 중복에 매끄러운 기능인 전환 기능을 위에서 설명한 대로 인정한다는 점이 특징으로 할 수 있다. 즉, 벡터 번들 E는 어떤 두 세트 U와 V에 대해 전환 함수인 것처럼 오픈 세트를 사소한 것으로 간주하여 커버를 인정하면 매끄럽다.

g_{UV:U\cap V\to \operatorname {GL}(k,\mathb {R} )

매트릭스 그룹 GL(k,R)의 부드러운 함수로서, Lie 그룹이다.

마찬가지로 전환 기능이 다음과 같은 경우:

그러면^r 벡터 번들은 C 벡터^r 번들이고,
그러면 실제 분석 벡터 번들은 실제 분석 벡터 번들이다(이것은 매트릭스 그룹이 실제 분석 구조를 갖도록 요구한다).
그러면 벡터 번들은 홀로모르픽 벡터 번들(이것은 복잡한 Lie 그룹이어야 함)이다.
그러면 대수 함수 벡터 번들은 대수 벡터 번들(이것은 행렬 그룹이 대수 그룹이어야 함)이다.

C-벡터^∞ 번들(E, p, M)은 더 일반적인 C-파이버^∞ 번들에 의해 공유되지 않는 매우 중요한 속성을 가지고 있다. 즉, v ∈ E의_x 접선 공간 T_v(E_x)는 섬유 E_x 자체로 자연적으로 식별할 수 있다. 이 식별은 다음과 같이 정의된 수직 리프트 vl_v: E_x → T_v(E_x)를 통해 얻는다.

\vmsname {v}w[f]:=\\frac {d}{dt}}\오른쪽 _{t=0}f(v+tw),\quad f\in C^{\infit }(E_{x}).

The vertical lift can also be seen as a natural C^∞-vector bundle isomorphism p*E → VE, where (p*E, p*p, E) is the pull-back bundle of (E, p, M) over E through p: E → M, and VE := Ker(p_*) ⊂ TE is the vertical tangent bundle, a natural vector subbundle of the tangent bundle (TE, $π$ _TE, E) of the total space E.

어떤 매끄러운 벡터 번들의 총 공간 E는 표준 벡터 장으로 알려진 자연 벡터 장 V_v := vlv를_v 가지고 있다. 좀 더 형식적으로 V는 ( $TE$ _TE, ,, E)의 매끄러운 부분이며, 또한 섬유화 메스칼라 곱셈에 의해 주어지는 Lie-group 작용(t, v) ↦ ev의^t 최소 생성기로 정의할 수도 있다. 표준 벡터장 V는 다음과 같은 방식으로 부드러운 벡터 번들 구조를 완전히 특징짓는다. 준비로서 X가 부드러운_x 다지관 M과 x ∈ M의 부드러운 벡터 필드인 경우, X = 0과 같은 선형 매핑에 유의한다.

C_{x}(X):T_{x}M\to T_{x}M;\quad C_{x}(X)Y=(\nabla _{Y}X)_{x}}}}}

M에 대한 선형 공변량 파생상품의 선택에 의존하지 않는다. 표준 벡터 필드 V on E는 공리를 만족한다.

V의 흐름(t, v) → φ^t_V(v)은 전체적으로 정의된다.
각 v ∈ V에 대해 고유한_t→∞ 림 φ^t_V(v) ∈ V가 있다.
C_v_v(V)∘C_v(V) = V = 0일 때마다 C_v(V)
V의 0 세트는 E의 부드러운 하위 관리본이며, 코디멘션은 C(V_v)의 등급과 같다.

반대로 E가 어떤 부드러운 다지관이고 V가 1-4를 만족하는 E의 부드러운 벡터장이라면 E에는 표준 벡터장이 V인 독특한 벡터 번들 구조가 있다.

매끄러운 벡터 번들(E, p, M)의 경우 접선 번들(TE, $π$ _TE, E)의 총 공간 TE는 자연적인 2차 벡터 번들 구조(TE_*, p, TM)를 가지고 있으며, 여기서 p는_* 표준 투영 p: E → M의 푸시 포워드다. 이차 벡터 번들 구조에서 벡터 번들 연산은 푸시-포워드 +:_* T(E × E) → TE 및 λ_*: TE → TE + 원래 덧셈 +: E × E → E 및 스칼라 곱셈 λ: E → E → E이다.

케이이론

콤팩트한 하우스도르프 위상학적 공간의 K-이론 그룹 $K (X)$ 는 우리가 정확한 시퀀스를 가질 때마다 관계를 갖는 복잡한 벡터 번들의 이소모르피즘 클래스 $[E]$ 에 의해 생성되는 아벨리아 그룹으로 정의된다.

A\to B\to C\to 0}

그때

[B]=[A]+[C]}

위상학 K 이론으로 KO-이론은 실제 벡터 번들을 고려하는 이 구조의 버전이다. 소형 지지대가 있는 K이론뿐만 아니라 상위 K이론 그룹도 정의할 수 있다.

라울 보트의 유명한 주기성 정리는 어떤 공간 $X$ 의 K 이론이 $X$ 의 이중 정지인 $SX$ 의² 이론과 이형성이 있다고 주장한다.

대수 기하학에서, 사람들은 체계 $X$ 의 일관성 있는 조각들로 구성된 K-이론 그룹과 위의 동등성 관계를 가진 체계 위의 벡터 번들의 K-이론 그룹을 고려한다. 기초적인 계획이 원활하다면 두 구조는 동일하다.

참고 항목

일반적인 생각

Grassmannian: 벡터 번들에 대한 공간 분류, 선 번들에 대한 투영 공간 분류
특성계급
분할원리
안정 묶음

위상 및 차동 기하학

게이지 이론: 벡터 번들과 주요 번들에 대한 연결과 물리학과의 관계에 대한 일반적인 연구.
연결: 벡터 번들의 섹션을 구별하는 데 필요한 개념.

대수 및 분석 기하학

메모들

^ Hatcher 2003, 사례 3.6.
^ 랭 1995.

원천

Abraham, Ralph H.; Marsden, Jerrold E. (1978), Foundations of mechanics, London: Benjamin-Cummings, see section 1.5, ISBN 978-0-8053-0102-1.
Hatcher, Allen (2003), Vector Bundles & K-Theory (2.0 ed.).
섹션 1.5를 참조하십시오Jost, Jürgen (2002), Riemannian Geometry and Geometric Analysis (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-42627-1.
Lang, Serge (1995), Differential and Riemannian manifolds, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94338-1.
Lee, Jeffrey M. (2009), Manifolds and Differential Geometry, Graduate Studies in Mathematics, vol. 107, Providence: American Mathematical Society, ISBN 978-0-8218-4815-9.
Lee, John M. (2003), Introduction to Smooth Manifolds, New York: Springer, ISBN 0-387-95448-1 5장 참조
Rubei, Elena (2014), Algebraic Geometry, a concise dictionary, Berlin/Boston: Walter De Gruyter, ISBN 978-3-11-031622-3.

외부 링크

[FOOTNOTEHatcher2003Example_3.6-1] Hatcher 2003, 사례 3.6.

[FOOTNOTELang1995-2] 랭 1995.

[1]

[2]

Search

벡터 번들

네임스페이스

더

목차

정의와 첫 번째 결과

전환 함수

서브번들

벡터 번들 형태론

섹션 및 로컬 무료 셰이브

벡터 번들에 대한 작업

추가 구조 및 일반화

부드러운 벡터 번들

케이이론

참고 항목

일반적인 생각

위상 및 차동 기하학

대수 및 분석 기하학

메모들

원천

외부 링크