확률분포
비율 분포(quotient distribution)는 알려진 두 개의 다른 분포를 가진 확률 변수 의 비율 의 분포로 구성되는 확률 분포 입니다.두 개의 (보통 독립적인) 랜덤 변수 X 와 Y가 주어졌을 때, 비율 Z = X /Y 로 형성되는 랜덤 변수 Z의 분포는 비율 분포입니다.
예 를 들어, 코시 분포(정규 비율 [citation needed 분포라고도 함)는 평균이 0인 두 정규 분포 변수의 비율로 나타납니다.검정 통계학에서 자주 사용되는 다른 두 가지 분포도 비율 분포입니다. t-분포 는 독립 카이 분포 랜덤 변수로 나눈 가우스 랜덤 변수에서 발생하는 반면, F-분포 는 독립 카이 제곱 분포 랜덤 변수 두 개의 비율에서 발생합니다. 보다 일반적인 비율 분포가 [1] [2] [3] [4] [5] [6] [7] [8] [9]
종종 비율 분포는 꼬리 가 무겁기 때문에 이러한 분포를 사용하고 관련 통계 검정을 개발하는 것이 어려울 수 있습니다. 중앙값 을 기반으로 하는 방법이 "해결 방법"[10]
확률변수대수 비율은 랜덤 변수에 대한 대수의 한 가지 유형입니다. 비율분포와 관련된 것은 상품분포 , 합분포 , 차분분포 등입니다. 일반적으로, 합, 차이, 곱 및 비율의 조합에 대해 이야기할 수 있습니다. 이러한 분포의 대부분은 멜빈 D에 설명되어 있습니다. 1979년 스프링어의 책 무작위 [8] 대수학
일반적인 숫자로 알려진 대수적 규칙은 무작위 변수의 대수에는 적용되지 않습니다. 예를 들어, 어떤 제품 이 C = AB 이고 비율 이 D = C/A이면 반드시 D 와 B의 분포 가 동일한 것은 아닙니다. 실제로 코시 분포에 대한 독특한 효과가 나타납니다.두 개의 독립적인 코시 분포(같은 척도 모수와 위치 모수가 0으로 설정됨)의 곱과 비율은 동일한 [8] 이는 코시 분포 자체를 0의 두 가우시안 분포의 비율 분포로 간주할 때 명확해집니다. 두 분포 {\ displaystyle C_{ C {\ {2}} C G displaystyle C_{1 G_{ G_{ 2 G G displaystyle C_{ G_{3}/G_ }
C 1 C 2 = G 1 / G 2 G 3 / G 4 = G 1 G 4 G 2 G 3 = G 1 G 2 × G 4 G 3 = C 1 × C 3 , {\displaystyle {\frac {C_{1}}{{C_{2}}={\frac {G_{1}}/{G_{2}}{{G_{3}}}={\frac {G_{1}G_{4}}{{2}}{G_{3}}={\frac {G_{1}}{{G_{2}}}\회 {\frac {G_{4}}{G_{3}}=C_{1}\회 C_{3}}} 여기 3 G G displaystyle {3 G_{4} G_{3 첫 번째 항은 두 코시 분포의 비율이고, 마지막 항은 두 분포의 곱입니다.
파생 합동 pX, Y x , y displaystyle }( ) p_{X, x, 변수 X, Y 의 합동 분포로부터 Z = X Y displaystyle Z X/
p Z ( z ) = ∫ − ∞ + ∞ y p X , Y ( z y , y ) d y . {\displaystyle p_{Z}(z)=\int _{-\infty}^{+\infty} y \,p_{X,Y}(zy,y)\,dy.} 두 변수가 독립적이면 pXY x , y pX x ) pY ( y ) displaystyle p_{XY}(x,y p_{X}(x)p_{Y}(y)}
p Z ( z ) = ∫ − ∞ + ∞ y p X ( z y ) p Y ( y ) d y . {\displaystyle p_{Z}(z)=\int _{-\infty}^{+\infty} y \,p_{X}(zy)p_{Y}(y)\,dy.} 이것은 간단하지 않을 수 있습니다. 예를 들어, 두 표준 가우스 샘플의 비율에 대한 고전적인 문제를 살펴봅니다. 공동 pdf는
p X , Y ( x , y ) = 1 2 π 익스피드 ( − x 2 2 ) 익스피드 ( − y 2 2 ) {\displaystyle p_{X,Y}(x,y)={\frac {1}{2\pi}}\exp \left(-{\frac {x^{2}}{2}}\right)\exp \left(-{\frac {y^{2}}\right)} Z = X Y {\displaystyle X/Y}
p Z ( z ) = 1 2 π ∫ − ∞ ∞ y 익스피드 ( − ( z y ) 2 2 ) 익스피드 ( − y 2 2 ) d y = 1 2 π ∫ − ∞ ∞ y 익스피드 ( − y 2 ( z 2 + 1 ) 2 ) d y {\displaystyle {\begin{aligned}p_{Z}(z)&={\frac {1}{2\pi}}\int _{-\infty}^{\infty}}\, y \,\exp \left{\frac {\left(zy\right)^{2}}\right)\,\exp \left{\frac {y^{2}}\right)\,dy\&={\frac {1}{2\pi}}\int _{-\infty}^{\infty}}\, y \,\exp \left{\frac {y^{2}\left(z^{2}+1\right){2}\right},dy\end{aligned}}} 알려진 정적분 ∫ 0 x c x 2 d x 12 textstyle \int {0}^{\infty}}\,x\,\exp left cx^{2}\right)\,θ frac {1}{2c}}
p Z ( z ) = 1 π ( z 2 + 1 ) {\displaystyle p_{Z}(z)={\frac {1}{\pi(z^{2}+1)}} 이 분포는 코시 분포 또는 n = 1인 학생 의 t 분포입니다.
멜린 변환은 또한 비율 [8]
양의 독립 변수의 경우 다음과 같이 진행합니다. 이 다이어그램은 분리 가능한 이변량 분포 x , y x , y x fy y ) displaystyle f_{x,y}(x,y f_{x}(x)f_{y}(y) 사분면 0 displaystyle ,y>0} 비율 X Y displaystyle X/Y x R {\displaystyle y = x/ 함수 x , x y displaystyle f_{x }(x,y 함수 Y displaystyle X/Y\leq } 높이 y의 수평 스트립 은 x = 0에서 x = fy y ) dy ≥ 0 Ry f xx textstyle f_{y}(y)dy\int {0}^{Ry}f_{x}(x)\,dx 둘째, 수평 스트립 을 전체적으로 위로 통합하면 선 위의 확률 볼륨을 얻을 수 있습니다.
F R ( R ) = ∫ 0 ∞ f y ( y ) ( ∫ 0 R y f x ( x ) d x ) d y {\displaystyle F_{R}(R)=\int _{0}^{\infty}f_{y}(y)\left(\int _{0}^{Ry}f_{x}(x)dx\right)dy} 마지막으로 R {\displaystyle } 대해 FR ( R ) displaystyle F_{R}(R)} 미분 pdf f R ) displaystyle f_{R}(R
f R ( R ) = d d R [ ∫ 0 ∞ f y ( y ) ( ∫ 0 R y f x ( x ) d x ) d y ] {\displaystyle f_{R}(R)={\frac {d}{dR}}\left[\int_{0}^{\infty}f_{y}(y)\left(\int_{0}^{Ry}f_{x}(x)dx\right)dy\right]} 차분화를 적분 내부로 이동합니다.
f R ( R ) = ∫ 0 ∞ f y ( y ) ( d d R ∫ 0 R y f x ( x ) d x ) d y {\displaystyle f_{R}(R)=\int _{0}^{\infty}f_{y}(y)\lefty\frac {d}{dR}}\int _{0}^{Ry}f_{x}(x)dx\right)dy} 그 이후로
d d R ∫ 0 R y f x ( x ) d x = y f x ( R y ) {\displaystyle {\frac {d}{dR}}\int_{0}^{Ry}f_{x}(x)dx=yf_{x}(Ry)} 그리고나서
f R ( R ) = ∫ 0 ∞ f y ( y ) f x ( R y ) y d y {\displaystyle f_{R}(R)=\int_{0}^{\infty}f_{y}(y)\;f_{x}(Ry)\;y\;dy} 예를 들어 다음과 같은 경우 ratio R의 pdf를 구합니다.
f x ( x ) = α e − α x , f y ( y ) = β e − β y , x , y ≥ 0 {\displaystyle f_{x}(x)=\alpha e^{-\alpha x},\;\;\;\;f_{y}(y)=\alpha e^{-\alpha y},\;\;\;x,y\geq 0} 비율의 누적분포 평가 우리는 가지고 있다.
∫ 0 R y f x ( x ) d x = − e − α x 0 R y = 1 − e − α R y {\displaystyle \int _{0}^{Ry}f_{x}(x)dx=-e^{-\alpha x}\vert _{0}^{Ry}=1-e^{-\alpha Ry}} 따라서
F R ( R ) = ∫ 0 ∞ f y ( y ) ( 1 − e − α R y ) d y = ∫ 0 ∞ β e − β y ( 1 − e − α R y ) d y = 1 − α R β + α R = R β α + R {\displaystyle{aligned} F_{R}(R)&=\int _{0}^{\infty}f_{y}(y)\left(1-e^{-\alpha Ry}\right)dy=\int _{0}^{\infty}\left(1-e^{-\alpha Ry}\left(1-e^{-\alpha Ry}\left)dy\&=1-{\alpha R}{\beta +\alpha R}}\&={\frac {{\tfrac}{\alpha }}\end{aligned}}} 차별화 쓰기. R은 R 의 pdf를 산출 합니다.
f R ( R ) = d d R ( R β α + R ) = β α ( β α + R ) 2 {\displaystyle f_{R}(R)={\frac {d}{dR}}\left({\frac {R}{\tfrac {\alpha}}{\alpha}}+R}\right)={\frac {\tfrac {\alpha}}{\left\tfrac {\alpha}}{\alpha}}+R\right)^{2}} 랜덤 비율의 모멘트 멜린 변환 이론에서 양의 반선 0 displaystyle \geq } 우리 아이덴티티 UV) E [ E {\displaystyle \operatorname {E} UV }] \operatorname ^{p}]\ U, V displaystyle ,\;V} 경우 \;\operator E} V^{p}]}. E X Y p displaystyle \operatorname {E} X/Y)^{p 같은 E [ XZ ) E X Y displaystyle \operatorname {E} XZ) 되도록 Y Z 설정 ^{p}]=\operatorname {E} X^{p}]\;\operatorname {E} Y^{-p 따라서 X p displaystyle ^{p} Y displaystyle ^{-p} Y {\displaystyle /Y} Y p displaystyle ^{-p} displaystyle } 기껏해야 E [ Y p 0 y fy dy textstyle \operatorname {E} Y^{-p int {0}^{\infty }y^{-p}f_{y}(y)\,dy
예를 들어, Gamma 분포 } 추출
x 1 e x Ωα ) displaystyle ^{\alpha }e^{-x}/\Gamma (\alpha displaystyle α + p Ωα displaystyle \Gamma (\alpha p Gamma (\alpha Z = Y {\displaystyl e Y^{-1}} 매개 β displaystyle \beta} Δ 1 β ) zβ e 1 displaystyle Gamma 1}(\beta)z^{ beta }e^{-1/ }
E [ Z p ] = E [ Y − p ] = Γ ( β − p ) Γ ( β ) , p < β . {\displaystyle \operatorname {E} [Z^{p}]=\operatorname {E} [Y^{-p}]={\frac {\Gamma (\camma -p)}{\Gamma (\camma )}},\;p<\camma .} 해당 순간을 곱하면 다음을 얻을 수 있습니다.
E [ ( X / Y ) p ] = E [ X p ] E [ Y − p ] = Γ ( α + p ) Γ ( α ) Γ ( β − p ) Γ ( β ) , p < β . {\displaystyle \operatorname {E} [(X/Y)^{p}]=\operatorname {E} [X^{p}]\;\operatorname {E} [Y^{-p}]={\frac {\Gamma(\alpha +p)}{\ 감마(\alpha )}}{\frac {\Gamma(\beta -p)}{\Gamma(\beta )}},\;p<\beta .} 독립적으로 두 감마 표본 X Y {\displaystyle X/Y}
f ' r , α , = B α , ) 1 r 1 1 r α displaystyle f_{\alpha'}(r,\alph a ,\δ B(\alpha,\γ)^{-1}r^{\alpha }(1 r)^{-(\alpha δ )}, 모멘트 ≥ R = α + p β {\displaystyle \operatorname {E} R ^ {p frac mathrm {B}(\alpha p,\δ )}{\mathrm {B}(\alpha, \n*}}} B α , α ) Δ β ) α β displaystyle \mathrm {B} (\alpha, \alpha ={\frac {\Gamma (\alpha Gamma camma )}{\Gamma (\ camma )}} {\ R = Δ β + p β β α p = Δ β Δ - p Δ β {\displaystyle \operatorname { p}] = {\frac Gamma + p )}{\Gamma (\alpha +\ )}}{\Bigg }{\frac {\ frac Gamma (\ \Gamma(\alpha )}{\Gamma(\alpha +\alpha = frac Gamma(\alpha +p Gamma(\alpha -p)}{\Gamma(\ 위의 순간들의 곱 .
랜덤 비율의 평균 및 분산 Mellin 변환 이론에서 파생된 제품 분포 섹션(위의 섹션 참조)에서 독립 변수의 제품 평균이 해당 평균의 제품과 동일하다는 것이 확인되었습니다.비율의 경우에는.
E ( X / Y ) = E ( X ) E ( 1 / Y ) {\displaystyle \operatorname {E}(X/Y)=\operatorname {E}(X)\operatorname {E}(1/Y)} 확률 분포의 관점에서 다음과 같은 값을 갖습니다.
E ( X / Y ) = ∫ − ∞ ∞ x f x ( x ) d x × ∫ − ∞ ∞ y − 1 f y ( y ) d y {\displaystyle \operatorname {E}(X/Y)=\int _{-\infty }^{\infty }π_{x}(x)\,π\times \int _{-\infty }^{\infty }y^{-1}f_{y}(y)\,dy} E 1 Y1 E Y displaystyle \operatorname {E} 1/Y)\neq frac {1}{\operatorname {E} Y)}}, y y y fy ( y) dy int {-\infty }^{\infty }f_{y}\,dy\neq frac {1}{\int {-\infty }^{y}\nfty nfty y}\,dy}}
독립 변수 비율의 분산은
Var ( X / Y ) = E ( [ X / Y ] 2 ) − E 2 ( X / Y ) = E ( X 2 ) E ( 1 / Y 2 ) − E 2 ( X ) E 2 ( 1 / Y ) {\displaystyle {\display{aligned}\operatorname {Var}(X/Y)&=\operatorname {E}([X/Y]^{2})-\operatorname {E^{2}(X/Y)\&=\operatorname {E}(X^{2})-\operatorname {E}(1/Y^{2})-\operatorname {E}^{2}(1/Y)\end{aligned}} 정규비율분포 비상관 중심정규비 X 와 Y가 독립적이고 평균이 0인 가우스 분포를 가질 때 비율 분포의 형태는 코시 분포 입니다.이는 Z = X Y tan {\displaystyle X/Y tan \theta } 설정 displaystyle \theta } 이변량 상관 관계가 없는 가우스 분포의 경우 다음과 같습니다.
p ( x , y ) = 1 2 π e − 1 2 x 2 × 1 2 π e − 1 2 y 2 = 1 2 π e − 1 2 ( x 2 + y 2 ) = 1 2 π e − 1 2 r 2 와 함께 r 2 = x 2 + y 2 {\displaystyle {\display{aligned}p(x,y)&={\tfrac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}\tfrac {1}{\sqrt {2\pi }}\tfrac {2}}\&={\tfrac {1}{2\pi }\&#e^{-{\frac {1}{2}}(x^{2}+y^{2})}\&={\tfrac {1}{2\pi }}e^{-{\frac {1}}r^{2}}{\tfrac {2}}}}r^{{2}=x^{2}+y^{2}}. }\end{aligned}} p( x , y displaystyle (x,y)} r 의 함수일 경우 θ {\displaystyle \theta} 밀도 / 2 {\ displaystyle [0,2\pi [0 pi] 확률 분포를 찾는 것으로 줄어듭니다.
Z = X / Y = 태닝한 θ {\displaystyle Z=X/Y=\tan \theta } 우리는, 가능성을 보존함으로써,
p z ( z ) d z = p θ ( θ ) d θ {\displaystyle p_{z}(z) dz = p_{\theta}(\theta) d\theta } 그리고 dz d 1 cos ≥ {\displaystyle d\theta 1 cos ^{2}\theta }
p z ( z ) = p θ ( θ ) d z / d θ = 1 2 π cos 2 θ {\displaystyle p_{z}(z)={\frac {p_{\theta}(\theta )}{dz/d\theta }}={\tfrac {1}{2\pi }}{\cos ^{2}\theta }} 설정 cos 1 tan 2 1 z {\textstyle cos ^{2 {\frac {1}{1+(\tan theta {\frac {1}{1+z^{
p z ( z ) = 1 / 2 π 1 + z 2 {\displaystyle p_{z}(z)={\frac {1/2\pi}{1+z^{2}}}} 여기에는 2라는 가짜 계수가 있습니다. 실제로 θ displaystyle \theta } displaystyle } 동일 한 z 값에 매핑되어 밀도가 두 배로 증가하고 최종 결과는
p z ( z ) = 1 / π 1 + z 2 , − ∞ < z < ∞ {\displaystyle p_{z}(z)={\frac {1/\pi}{1+z^{2}},\;-\infty <z<\infty } 두 정규 분포 중 하나가 중심이 아닌 경우 비율 분포에 대한 결과는 훨씬 더 복잡하며 David Hinkley 가 [6] 제시 한 간결한 형태로 아래에 제시됩니다. 그러나 비율에 대한 삼각법 방법은 밀도가 반지름 x 2 y textstyle {\sqrt {x 2 확장 됩니다. }}}} 학생 t 분포의 비율로 확장되지 않습니다.
비상관 비중심정규비 상관관계 X , Y 0 displaystyle operatorname {cor} X, 0 변수 X = N (μ , σ) 및 Y = N (μ , σ) 비율 Z = X /Y 의 확률 밀도 함수는 여러 출처에서 도출된 정확한 다음 식으로 제공됩니다.
p Z ( z ) = b ( z ) ⋅ d ( z ) a 3 ( z ) 1 2 π σ x σ y [ Φ ( b ( z ) a ( z ) ) − Φ ( − b ( z ) a ( z ) ) ] + 1 a 2 ( z ) ⋅ π σ x σ y e − c 2 {\displaystyle p_{Z}(z)={\frac {b(z)\cdot d(z)}{a^{3}(z)}}{\frac {1}{{\sqrt {2\pi}}}\displaystyle p_{x}\displaystyle {y}}\left[\ Phi \left({\frac {b(z))}{a(z)}\right)-\Phi \left(-{\frac {b(z)}{a(z)}\right)\right]+{\frac {1}{a^{2}(z)\cdot \pi \sigma _{x}\sigma _{y}}e^{-{\frac {c}}} 어디에
a ( z ) = 1 σ x 2 z 2 + 1 σ y 2 {\displaystyle a(z)={\sqrt {{\frac {1}{\display _x}^{2}}}z^{2}+{\frac {1}{\displaystyle {y}^{2}}}} b ( z ) = μ x σ x 2 z + μ y σ y 2 {\displaystyle b(z)={\frac {\mu _{x}}{\mu _{x}^{2}}z+{\frac {\mu _{y}}{\mu _{y}^{2}}} c = μ x 2 σ x 2 + μ y 2 σ y 2 {\displaystyle c={\frac {\mu _{x}^{2}}{\mu _{x}^{2}}}+{\frac {\mu _{y}^{2}}{\mu _{y}^{2}}}} d ( z ) = e b 2 ( z ) − c a 2 ( z ) 2 a 2 ( z ) {\displaystyle d(z)=e^{\frac {b^{2}(z)-ca^{2}(z)}{2a^{2}(z)}}} 그리고 Δ{\displaystyle \Phi} 정규 누적 분포 함수입니다.
Φ ( t ) = ∫ − ∞ t 1 2 π e − 1 2 u 2 d u . {\displaystyle \Phi(t)=\int _{-\infty}^{t}\,{\frac {1}{\sqrt {2\pi}}}e^{-{\frac {1}{2}u^{2}}\du\,} 몇 가지 가정(일반적으로 실제 적용에서 충족됨) 하에서 PDF에 대한 매우 정확 한 솔리드 근사치 를 도출할 수 있습니다. 주요 이점은 공식 복잡성 감소, 폐쇄형 CDF, 단순 정의된 중위수, 잘 정의된 오류 관리 등입니다. 심플함을 위해 p μ x {\displaystyle mu _{x}}{\sqrt {2}}\mu {x q y 2 displaystyle mu _{y}}{\sqrt {2}}\mu {y}}, r μ x displaystyle frac mu _x}{\mu {y 그러면 상관 관계가 없는 비 중심 정규 비율 PDF에 대한 소위 솔리드 p z ) displaystyle p_{Z}^{\dagger z)} p Z † ( z ) = 1 π p e r f [ q ] 1 r 1 + p 2 q 2 z r ( 1 + p 2 q 2 [ z r ] 2 ) 3 2 e − p 2 ( z r − 1 ) 2 1 + p 2 q 2 [ z r ] 2 {\displaystyle p_{Z}^{\dagger }(z)={\frac {1}{\sqrt {\pi}}}{\frac {p}{\mathrm {erf}[q]}{{r}}{\frac {1}{r}}{\frac {1+{\frac {p^{2}}{q^{r}}{\left(1+{\frac {p^{2}}}{{q^{2}}}}\left[{\frac {z}{r}}\right]^{\frac {3}{2}}}}^{-{\frac {p^{2}}\left\frac {z}{r}-1\right)^{2}}}^{1+{\frac {p^{2}}{q^{2}}}\left[{\frac {z}}\right]^{2}}}}}. 특정 조건에서는 [12] σ z 2 = μ x 2 μ y 2 ( σ x 2 μ x 2 + σ y 2 μ y 2 ) {\displaystyle \displaystyle \display _{z}^{2}={\frac {\mu _{x}^{2}}\left({\frac {\mu _{x}^{2}}{\mu _{x}^{2}}+{\frac {\mu _{y}^{2}}{\mu _{y}^{2}}\right)} 상관 중앙정규비 위 식은 변수 X와 Y가 상관 관계에 있을 때 더 복잡해집니다.μ μ 0 displaystyle \mu {x mu {y 0 displaystyle \mu {X}\neq \mu _{ displaystyle \rho neq } 경우
p Z ( z ) = 1 π β ( z − α ) 2 + β 2 , {\displaystyle p_{Z}(z)={\frac {1}{\pi }}{\frac {\pi}}{(z-\alpha)^{2}+\frac ^{2}}}} 여기서 ρ 는 X 와 Y 사이 의 상관계수이고
α = ρ σ x σ y , {\displaystyle \alpha =\rho {\frac {\display_{x}}{\display_{y}},} β = σ x σ y 1 − ρ 2 . {\displaystyle \displaystyle \displaystyle = {\frac {\display_{x}}{\display_{y}}{\sqrt {1-\rho ^{2}}}} 복잡한 분포는 또한 쿰머의 합류 초기하학 함수 또는 헤르마이트 [9]
상관 비중심정규비 상관 관계가 있는 비중심 정규 비율에 대한 근사치 Katz(1978)는 로그 도메인으로의 변환을 제안했습니다(아래 이항 섹션 참조). 비율을 다음과 같이 하라.
T ~ μ N ( 0 , σ x 2 μ y N ( 0 , σ y 2 = μ x X μ + Y μ x y 1 X μ x Y μ {\displaystyle T\sim {\frac {\mu _{x}+\mathbb {N} (0,\mus _{y}^{2})}{\mus _{y}+\mathbb {N} (0,\mus _{y}^{2 } frac {\mu _{x}+X}{\mu _{y}+ Y}}={\frac mu x}}{\mu {y}}{\frac {1+{\frac {X}}{\mu _{x 1+{\frac }{\mu _{y 로그를 사용
로그. e ( T ) = 로그. e ( μ x μ y ) + 로그. e ( 1 + X μ x ) − 로그. e ( 1 + Y μ y ) . {\displaystyle \log _{e}(T)=\log _{e}\left({\frac {\mu _{x}}{\mu _{y}}\right)+\log _{e}\left(1+{\frac {X}{\mu _{x}}\right)-\log _{e}\left(1+{\frac {Y}{\mu _{y}}\right)} 로그 {\displaystyle \log {e}(1+\ -{\frac 2}}}}+{\frac {\ ^{3}}+\cdots }
로그. e ( T ) ≈ 로그. e ( μ x μ y ) + X μ x − Y μ y ∼ 로그. e ( μ x μ y ) + N ( 0 , σ x 2 μ x 2 + σ y 2 μ y 2 ) . {\displaystyle \log _{e}(T)\근접 \log _{e}\left({\frac {\mu _{x}}{\mu _{y}}\right)+{\frac {X}{\mu _{x}}-{\frac {Y}}\sim \log _{e}\left({\frac {\mu _{x}}{\mu _{y}}\right)+\mathbb {N} \left(0,{\frac {\frac {\sigma _{x}^{2}}{\mu _{x}^{2}}}+{\frac {\sigma _{y}^{2}}{\mu _{y}^{2}}\right}). 또는 Geary(1930)는 다음과 같이 제안했습니다.
t ≈ μ y T − μ x σ y 2 T 2 − 2 ρ σ x σ y T + σ x 2 {\displaystyle t\approx {\frac {\mu _{y}T-\mu _{x}}{\sqrt {\sigma _{y}^{2} T^{2}-2\rho \sigma _{x}\sigma _{y}T+\sigma _{x}^{2}}}} 는 대략적 으로 표준 [1] 분포 를 갖습니다. 이 변환을 Geary-Hinkley 변환이라고 합니다. Y가 기본적 μy > 3 displaystyle \mu {y}> 3\sigma _ }} 않을 경우 근사치가 좋습니다.
정확한 상관 관계가 있는 비중심 정규 비율 기어리는 상관 비율 displaystyle } 값 μ x 0 displaystyle +\mu {x}<0} displaystyle } 근사치 필러의 나중 상관 비율 분석은 정확하지만 현대 수학 패키지와 함께 사용될 때 주의가 필요하며 마르살리아 방정식의 일부에서 비슷한 문제가 발생할 수 있습니다. 팜-지아는 이 방법들에 대해 철저하게 논의했습니다. 힝클리의 상관 결과는 정확하지만 아래에 나타나 있듯이 상관 비율 조건은 단순히 상관이 없는 조건으로 변환될 수 있으므로 전체 상관 비율 버전이 아닌 위의 단순화된 힝클리 방정식만 필요합니다.
비율은 다음과 같습니다.
z = x + μ x y + μ y {\displaystyle z={\frac {x+\mu _{x}}{y+\mu _{y}}} x, y displaystyle ,y} x 2, 2 displaystyle \sigma {x}^{2},\sigma {y}^{ 2 }, , Y {\displaystyle ,Y} 평균 μ , y . displaystyle \mu {x},\mu {y}. } ', y displaystyle displaystyle ', y 없고 ' 편차 = x = ρ y σ ' σ y displaystyle '}
σ x ′ = σ x 1 − ρ 2 . {\displaystyle \display_{x}'=\display_{x}{\sqrt {1-\rho ^{2}}}} 비율:
z = x ′ + ρ y σ x / σ y + μ x y + μ y {\displaystyle z = {\frac {x'+\rhoy\display _{x}/\displaystyle _{y}+\mu _{x}}{y+\mu _{y}}} 는 이 변환 하에서 불변하며 동일한 pdf를 유지합니다. 분자 {\displaystyle }
x ′ + ρ y σ x / σ y + μ x = x ′ + μ x − ρ μ y σ x σ y + ρ ( y + μ y ) σ x σ y {\displaystyle {x'+\rhoy\mu _{x}}/\displaystyle {x'+\mu _{x}}=x'+\mu _{x}-\rho \mu _{y}{\frac {\displaystyle {x'}{\displaystyle {x}}+\rho (y+\mu _{y}){\frac {\displaystyle {x}}} 갖기 위해
z = x ′ + μ x ′ y + μ y + ρ σ x σ y {\displaystyle z={\frac {x'+\mu _{x}}{y+\mu _{y}}}+\rho {\frac {\displaystyle {x}}} 여기 μ μ μ {\textstyle \mu '_ mu _{x}-\rho mu _{ frac {\tax {x}}{\tax {y}}}, z 는 이제 불변의 z-벡터를 가진 상관없는 중심 정규 샘플의 비율이 되었습니다.
마지막으로, 명확하게 말하면, 상관 변수에 대한 비율 displaystyle } ′, μ x ′, y , μ displaystyle nx}',\mu _{x}',\mu {y}}, displaystyle rho ' 0 z displaystyle } ant {\displaystyle -\rho frac {\display_{x}}{\displaystyle}}}.
비율 x/y 를 제공하는 상관 이변량 가우스 분포(척도로 표시하지 않음)의 등고선
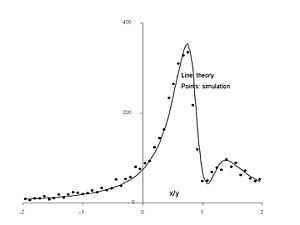
가우시안 비 z의 pdf 및 에 대한 시뮬레이션(점) σ x = σ y = 1 , μ x = 0 , μ y = 0.5 , ρ = 0.975 {\displaystyle \displaystyle \display _{x}=\display_{y}=1,\mu _{x}=0,\mu _{y}=0.5,\rho =0.975} 위의 그림은 음영 처리된 쐐기가 주어진 비율 y , μ x 0 μ y 0.5 , .975 displaystyle } \mu {y} 1,\mu {x 0,\mu {y 0.5,\rho 0.975} r , displaystyle /y\in [r, 분포 r+\ ]}. 논의 중인 방정식과 힝클리 방정식을 결합한 이론적 분포는 5,000개의 샘플을 사용한 시뮬레이션 결과와 매우 일치합니다. 위 z x displaystyle z 반대로 x/ y{\displaystyle /y} 줄어들면
이 변형은 Geary(1932)가 그의 eqn 8에서 부분적인 결과로 사용한 것과 동일하지만 그의 파생과 한계는 거의 설명되지 않았습니다. 따라서 이전 섹션에서 가우스성을 근사화하기 위한 기어리 변환의 첫 번째 부분은 실제로 정확하며 Y 의 양에 의존하지 않습니다. 오프셋 결과는 첫 번째 섹션에서 "코시" 상관 0-평균 가우스 비율 분포와 일치합니다. Marsaglia는 동일한 결과를 적용했지만 이를 달성하기 위해 비선형 방법을 사용했습니다.
복소정규비 Baxley et al.[13] 원대칭 복소 정규분포변수 의 비율을 구하였으며, 이후 0-평균이 아닌 경우와 비대칭인 [14] 상관된 0-평균인 경우 x, y 의 합동 분포는
f x , y ( x , y ) = 1 π 2 Σ 익스피드 ( − [ x y ] H Σ − 1 [ x y ] ) {\displaystyle f_{x,y}(x,y)={\frac {1}{\pi ^{2} \Sigma}}}\exp \left{\signal{bmatrix}x\y\end{bmatrix}}^{ H}\Sigma^{-1}{\bmatrix}x\y\end{bmatrix}}\right)} 어디에
Σ = [ σ x 2 ρ σ x σ y ρ ∗ σ x σ y σ y 2 ] , x = x r + i x i , y = y r + i y i {\displaystyle \Sigma = {\display{bmatrix}\sigma _{x}^{2}&\rho \sigma _{x}\sigma _{y}\sigma _{x}\sigma _{y}^{2}\end{bmatrix}},\;x=x_{r}+ix_{i},\;y=y_{r}+i_{i} ( ⋅ H {\displaystyle (\cdot )^{ H}}
ρ = ρ r + i ρ i = E ( x y ∗ σ x σ y ) ∈ C ≤ 1 {\displaystyle \rho =\rho _{r}+i\rho _{i}=\operatorname {E} {\bigg(}{\frac {xy^{*}}{\frac _{x}\rong _{y}}{\bigg}\;\n\in \;\left \mathbb {C} \right \leq 1} Z = X Y {\displaystyle X/Y}
f z ( z r , z i ) = 1 − ρ 2 π σ x 2 σ y 2 ( z 2 σ x 2 + 1 σ y 2 − 2 ρ r z r − ρ i z i σ x σ y ) − 2 = 1 − ρ 2 π σ x 2 σ y 2 ( z σ x − ρ ∗ σ y 2 + 1 − ρ 2 σ y 2 ) − 2 {\displaystyle {\display{aligned}f_{z}(z_{r), z_{i})&={\frac {1- \rho ^{2}}{\pi \prox}^{2}\prox_{y}^{2}}{\biggr(}{\frac {z^{2}}{\frac {z^{x}^{2}}}+{\frac {1}{\prox}z_{r}}-2{\frac {\rho _{r}z_{i}{i}}{\prox}\prox}{y}}}{\biggr}}^{-2}\&={\frac {1- \rho ^2}}{\pi \prox}^{2}\prox}^{{y}^{2}}{\biggr(})}{\frac {z}{\prox}}}-{\frac {rho ^*}}{\s. igma _{y}}{\Biggr }^{2}+{\frac {1- \rho ^{2}}{\sigma _{y}^{2}}{\Biggr )}^{-2}\end{aligned}} σ x {\displaystyle \display_{x display_{y}}
f z ( z r , z i ) = 1 − ρ 2 π ( z − ρ ∗ 2 + 1 − ρ 2 ) 2 {\displaystyle f_{z}(z_{r},z_{i})={\frac {1- \rho ^{2}}{\pi \left(\;\;\; z-\rho ^{*} ^{2}+1- \rho ^{2}\right)^{2}}} CDF에 대한 추가 폐쇄형 결과도 제공됩니다.
상관된 복소 변수의 비율 분포, rho = 0.7 exp(ipi/4). 그래프는 상관 계수가 θ = 0. 7 i {\displaystyle \rho 0.7\exp(i\pi 4 pdf 피크는 축척된 {\displaystyle \rho
로그 정규 분포 비율 독립적이거나 상관된 로그 정규식의 비율은 로그 정규식입니다. 이는 X displaystyle {1 }} 2 displaystyle { 가 ) 로그 정규 분포 ln X 1) displaystyle \ ln (X_{ 1 ln 2) displaystyle \ln(X_{ 독립적이거나 로그가 이변량 정규 분포를 따르는 경우 비율의 로그는 정규 분포를 따르는 독립적이거나 [note 1]
이는 X 1 displaystyle {1 displaystyle X_{ 이것 Xi displaystyle X_ } 양 [15] 지브라트의 법칙이라고 도 불리는 곱셈 중심 극한 정리의 일반적인 결과입니다.
균일비율분포 두 개의 독립적인 랜덤 변수가 균일한 분포를 따르는 경우, 예를 들어,
p X ( x ) = { 1 0 < x < 1 0 그렇지않으면 {\displaystyle p_{X}(x)={\begin{case}1&0<x<1\0&{\text{otherwise}}\end{case}} 비율분포는
p Z ( z ) = { 1 / 2 0 < z < 1 1 2 z 2 z ≥ 1 0 그렇지않으면 {\displaystyle p_{Z}(z)={\begin{case}1/2\qquad &0<z<1\{\frac {1}{2z^{2}}}\qquad &z\geq 1\0\qquad &{\text{case}}\end{case}} 코시비분포 두 개의 독립 랜덤 변수 가 각각 중위수가 0이고 형상 인자 가 {\displaystyle } 코시 분포를 따르는 경우
p X ( x a ) = a π ( a 2 + x 2 ) {\displaystyle p_{X}(xa)={\frac {a}{\pi(a^{2}+x^{2}}}} 그러면 랜덤 변수 X Y {\displaystyle X Y}
p Z ( z a ) = 1 π 2 ( z 2 − 1 ) ln ( z 2 ) . {\displaystyle p_{Z}(za)={\frac {1}{\pi ^{2}(z^{2}-1)}}\ln(z^{2}).} 이 분포는 {\displaystyle } 의존 [8] 비율 분포는 랜덤 변수 X {\displaystyle XY 분포 와 비슷하지만 같지는 않습니다.
p W ( w a ) = a 2 π 2 ( w 2 − a 4 ) ln ( w 2 a 4 ) . {\displaystyle p_{W}(wa)={\frac {a^{2}}{\pi ^{2}(w^{2}-a^{4}}}\ln \left({\frac {w^{2}}{a^{4}}\right).} [8] 일반적으로 두 독립 랜덤 변수 X 와 Y가 각각 중위수가 0이고 형상 인자가 각각 displaystyle } b {\displaystyle } 코시 분포 를 따르는 경우:
랜덤 변수 X Y {\displaystyle X Y} p Z ( z a , b ) = a b π 2 ( b 2 z 2 − a 2 ) ln ( b 2 z 2 a 2 ) . {\displaystyle p_{Z}(za,b)={\frac {ab}{\pi ^{2}(b^{2}z^{2}-a^{2}}}\ln\leftfrac {b^{2}z^{2}}{a^{2}}\right).} 랜덤 변수 XY {\displaystyle XY} 제품 분포는 p W ( w a , b ) = a b π 2 ( w 2 − a 2 b 2 ) ln ( w 2 a 2 b 2 ) . {\displaystyle p_{W}(wa,b)={\frac {ab}{\pi ^{2}(w^{2}-a^{2}b^{2}}}\ln\leftfrac {w^{2}}{a^{2}b^{2}}\right)}. 비율 분포에 대한 결과는 displaystyle } ( 1b 대체 . displaystyle frac {1}{b}}}
표준정규 대 표준균일의 비율 X가 표준 정규 분포를 가지고 Y가 표준 균일 분포를 가지면 Z = X / Y 는 확률 밀도 함수와 함께 슬래시
p Z ( z ) = { [ φ ( 0 ) − φ ( z ) ] / z 2 z ≠ 0 φ ( 0 ) / 2 z = 0 , {\displaystyle p_{Z}(z)={\begin{case}\left[\varphi (0)-\varphi (z)\right]/z^{2}\neq 0\\varphi (0)/2\neq &z=0,\\\end{case}} 여기서 ρ(z )는 표준 정규 [17]
카이제곱, 감마, 베타 분포 G 를 정규(0,1) 분포라고 하고 , Y와 Z 를 각각 m 과 n 자유도 를 갖는 치안정 분포라고 하고 , 모두 독립적이며, f x , k x k 1 x 22 k2 k 2) displaystyle f_{\chi }(x,k frac {x}{2}}e^{-x/2}{2^{k/2}\Gamma (k/2
GY m m {\ displaystyle frac {G}{\sqrt {Y/m}}\simt_{m} 학생 t 분포 Y m n = Fm, n displaystyle frac {Y/m } {Z/n F_{m,n}, Fisher's F-검정 분포 YY Z β m , n displaystyle frac {Y}{Y+Z}}\sim \beta ({\tfrac {m}{2}}, tfrac {n}{2}}} 베타 YZ ' m2 n2 displaystyle \;\;{\frac {Y}{Z}}\sim \beta '({\tfrac {m}{2}},{\tfrac {n}{2}}} 표준 분포V 2 displaystyle {1}\sim {\chi'}_{k_{1}}^{2}(\lambda 비중심 치 제곱 분포 , V k 2 displaystyle V_{2}\sim {\chi'}_{k_{ 2 0) 및 displaystyle 1} displaystyle V_{
V k V k F k 1 , k 2 λ displaystyle frac {V_{1}/k_{1}}{V_{2}}\sim '_{k_{1}, k_{2}}(\lambda 비중심 F 분포 입니다. mn F m , n = β ′(m2 n2 또는 F m , n β m2 n2 1 , nm displaystyle frac {m}{n}, ' _ {m,n beta '({\tfrac {m}{2}}, {\tfrac {n}{2}}{\tfrac {m,n beta '({\tfrac {m}{2}}, tfrac {n}{m {\tfrac n}{ m }}, n '\displaystyle _{m,n m, n 자유도와 함께 합니다.
F-표에서 발견되는 피셔 밀도의 CDF는 베타 프라임 분포 기사에서 정의됩니다. 오른쪽 꼬리에 m = 3, n = 4 및 5% 확률 로 F-검정표를 입력하면 임계 값은 6.59입니다. 이것은 적분과 일치합니다.
F 3 , 4 ( 6.59 ) = ∫ 6.59 ∞ β ′ ( x ; m 2 , n 2 , 1 , n m ) d x = 0.05 {\displaystyle F_{3,4}(6.59)=\int _{6.59}^{\infty}}\not '(x;{\tfrac {m}{2}},{\tfrac {n}{2}},1,{\tfrac {n}{m}},[0.05} 임의 의 모양 매개 변수 α 와 α를 갖는 감마 분포 U 와 V 및 그 척도 매개 변수가 둘 다 단일성으로 설정된 경우, Ω α 1 , ), Ω α 2 , displaystyle U\sim alpha _{1}, ), V\sim (\ alpha _{2}, 1 α 1 e Ω α {\displaystyle Gamma (x;\ 1 ) frac x^{\alpha -1}e^{-x} }{\Gamma(\alpha )}}},
U U + V ∼ β ( α 1 , α 2 ) , 기대. = α 1 α 1 + α 2 {\displaystyle {\frac {U}{U+V}}\sim \sim (\alpha _{1},\alpha _{2}),\qquad {\text{기대}}}={\frac {\alpha _{1}}{\alpha _{1}+\alpha _{2}}} U V ∼ β ′ ( α 1 , α 2 ) , 기대. = α 1 α 2 − 1 , α 2 > 1 {\displaystyle {\frac {U}{V}}\sim \displaystyle '(\alpha _{1},\alpha _{2}),\qquad \qquad {\text{기대}}}={\frac {\alpha _{1}}{\alpha _{2}-1}},\;\alpha _{2}>1} V U ∼ β ′ ( α 2 , α 1 ) , 기대. = α 2 α 1 − 1 , α 1 > 1 {\displaystyle {\frac {V}{ U}}\sim \sim \sim '(\alpha _{2},\alpha _{1}),\qquad \qquad {\text{기대}}}={\frac {\alpha _{2}}{\alpha _{1}-1}},\;\alpha _{1}>1} U x α 1 displaystyle \sim \Gamma (x;\alpha,1 x α x α 1 e displaystyle U\sim \Gamma (x;\alpha,\theta frac {x^{\alpha -1}e^{-{\frac {x}{\theta }}}{\theta k}\Gamma alpha )}. 척도 매개 변수입니다.
U α , V α , displaystyle \sim \Gamma (\alpha 1},\theta {1}),\;V\sim \Gamma (\alpha 2},\theta {2 {\displaystyle \theta }
U θ 1 U θ 1 + V θ 2 = θ 2 U θ 2 U + θ 1 V ∼ β ( α 1 , α 2 ) {\displaystyle {\frac {U}{\frac {{1}}{{\frac {U}{\theta _{1}}}+{\frac {V}{\theta _{2}}}={\frac {\theta _{2}}}{\frac {\frac {\theta _{2}} U}{\theta _{2}U+\theta _{1}V}}\sim \beta (\alpha _{1},\alpha _{2}}} U θ 1 V θ 2 = θ 2 θ 1 U V ∼ β ′ ( α 1 , α 2 ) {\displaystyle {\frac {U}{\frac {{1}}}{\frac {V}{\theta _{2}}}={\frac {\theta _{1}}}{\frac {U}{V}}\sim \sim \sim \sim \sim '(\alpha _{1} 따라서
U V ∼ β ′ ( α 1 , α 2 , 1 , θ 1 θ 2 ) 그리고. E [ U V ] = θ 1 θ 2 α 1 α 2 − 1 {\displaystyle {\frac {U}{V}}\sim \displaystyle {\alpha _{1},\alpha _{2}},{\frac {\theta _{2}})\displaystyle {\frac {\frac {U}{V}\right]={\frac {\theta _{2}}{\frac {\alpha _{1}}{\alpha _{2}-1}}}{\frac {\alpha _{2}-1}}}. 여기 ′ α β , p ) display style alpha,\lamba,p,q)} 일반화된 베타 프라임 분포를 나타냅니다.
위에서 X β α , α 2 ,1 , 1 ) β ′(α , α 2 ) displaystyle sim \beta '(\alpha 1},\alpha 2}, ,1)\equiv \beta '(\alpha 1},\alpha {2})} 경우 β α 1 α 2 , , {\displaystyle X\ beta alpha _{ alpha _{2}, theta )}
β ′ ( x ; α 1 , α 2 , 1 , R ) = 1 R β ′ ( x R ; α 1 , α 2 ) {\displaystyle \context '(x;\alpha _{1},\alpha _{2},1,R)={\frac {1}{R}}\beta '({\frac {x}{R}};\alpha _{1},\alpha _{2}} U α , V α , displaystyle \sim \Gamma (\alpha 1},\theta {1}), V\sim \Gamma (\alpha 2},\theta {2})}
U V ∼ 1 R β ′ ( x R ; α 1 , α 2 ) = ( x R ) α 1 − 1 ( 1 + x R ) α 1 + α 2 ⋅ 1 R B ( α 1 , α 2 ) , x ≥ 0 {\displaystyle {\frac {U}{V}}\sim {\frac {1}{R}}\beta '({\frac {x}{R}};\alpha _{2})={\frac {\left}\frac {x}{R}\right)^{\alpha _{1}-1}}\right)^{\left(1+{\frac {x}{R}}\right)^{\alpha _1}+\alpha _{2}}}\cdot {\frac {1}{\;R\;B(\alpha _1},\alpha _{2}}},\;x\geq 0} 어디에
R = θ 1 θ 2 , B ( α 1 , α 2 ) = Γ ( α 1 ) Γ ( α 2 ) Γ ( α 1 + α 2 ) {\displaystyle R={\frac {\theta _{1}}{\theta _{2}},\;\;B(\alpha _{1},\alpha _{2})={\frac {\Gamma(\alpha _{1})\Gamma(\alpha _{2})}{\Gamma(\alpha _{1}+\alpha _{2}}}} 레일리 분포 X, Y 가 레일리 분포 f r / 2 er 2 , r 0 displaystyle f_{r}(r r/\ ^{2})e^{-r^{2}/2\ ^{2}},\;\;r\geq } 비율 Z = X /Y 는 분포를 따릅니다.
f z ( z ) = 2 z ( 1 + z 2 ) 2 , z ≥ 0 {\displaystyle f_{z}(z)={\frac {2z}{(1+z^{2})^{2}}},\;\;z\geq 0} 그리고 cdf를 가지고 있습니다.
F z ( z ) = 1 − 1 1 + z 2 = z 2 1 + z 2 , z ≥ 0 {\displaystyle F_{z}(z)=1-{\frac {1}{1+z^{2 }}}={\frac {z^{2}}{1+z^{2}},\;\;\;z\geq 0} Rayleigh 분포는 스케일링을 유일한 매개변수로 사용합니다. Z = α Y {\displaystyle alpha /Y}
f z ( z , α ) = 2 α z ( α + z 2 ) 2 , z > 0 {\displaystyle f_{z}(z,\alpha )={\frac {2\alpha z}{(\alpha +z^{2})^{2}}},\;\;z>0} 그리고 cdf를 가지고 있습니다.
F z ( z , α ) = z 2 α + z 2 , z ≥ 0 {\displaystyle F_{z}(z,\alpha )={\frac {z^{2}}{\alpha +z^{2}},\;\;\;z\geq 0} 분수 감마 분포(chi, 카이제곱, 지수, Rayleigh 및 Weibull 포함) 일반화된 감마 분포는
f ( x ; a , d , r ) = r Γ ( d / r ) a d x d − 1 e − ( x / a ) r x ≥ 0 ; a , d , r > 0 {\displaystyle f(x;a,d,r)={\frac {r}{\Gamma(d/r)a^{d}}x^{d-1}e^{-(x/a)^{r}}\;x\geq 0;\;a,\;d,\;r>0} 여기에는 분수 파워를 포함하는 정규 감마, 카이, 카이 제곱, 지수, 레일리, 나카가미 및 웨이불 분포가 포함됩니다. 여기 서 a는 속도 매개변수가 아니라 척도 매개변수이고 d는 형상 매개변수입니다.
U f x a 1 ,d 1 , r ), f x a 2 ,d , r 이 독립적 W U V displaystyle \sim x;a_{1},d_{1},\;\;V\sim (x;a_{2},d_{2},r){\text{ 독립적이고 }}W U/V} g w a 1 2 d 2 d r d 2 w d 1 1 2 1 r w r d 1 d 2 w0 textstyle (w frac {r\left}\frac {a_{1}}\right) ^{d_{2}}}{B\left({\frac {d_{1}}{r}}}{\frac {d_{2}}{r}}{\right)}}{\frac {w^{-d_{2}-1}}{\left(1+\left({\frac {a_{2}}}{a_{1}}\right)^{-r}^{\frac {d_1}+d_{2}^{frac {d_1}+right)^{frac {d_1}+d_{2 } }}:{r}}},\;\;w>0} 여기 u , v u v u v displaystyle u,v frac Gamma (u)\Gamma (v)}{\Gamma (u v)}} 다양한 스케일링 인자의 혼합물 모델링 위의 비율에서 Gamma 표본 U 표본 크기 1 α {\displaystyle alpha _{ alpha _{ 동일 분포 α e Ω ) displaystyle {\frac alpha -1}e^{-{\frac theta theta ^{k Gamma alpha {\displaystyle theta
U 다른 X U V 11 B displaystyle frac {U}{U+V frac {1}{1+B}}, ~ α , V α , displaystyle \sim \Gamma (\alpha {1},\theta ), V\sim \Gamma (\alpha {2},\theta ),\theta } 위 B e a α , α 2 B V UB t a' α , α 1 displaystyle \sim (\alpha 1}) ,\alpha_{2},B=V/U\sim '(\alpha_{2},\alpha_{1
임의 Y U 11 , 0 ≤ displaystyle \sim frac {U}{U+\varphi {\frac }{ varphi },\;\;0\leq \leq }
B 1 X {\displaystyle frac {1-X}{X}} 있으며 Y X 1 - , d d 1 2 displaystyle frac {X}{\varphi 1-\varphi )X}}, dY/dX frac varphi (1-\varphi )X}^{2}}} 됩니다
X를 Y 변환 f Y f X X d d X X α 1 ,α 1 2 displaystyle f_{Y}(Y frac {f_{X}(X)} dY/dX frac {\alpha _{1},\alpha 2}} varphi /[\varphi +(1-\varphi )X]^{{2}}}}
참고 Y 1 - displaystyle frac varphi }{1 \varphi ) Y}}}
f Y ( Y , φ ) = φ [ 1 − ( 1 − φ ) Y ] 2 β ( φ Y 1 − ( 1 − φ ) Y , α 1 , α 2 ) , 0 ≤ Y ≤ 1 {\displaystyle f_{Y}(Y,\varphi )={\frac {\varphi }{[1-(1-\varphi )Y]^{2}}\beta \left({\frac {\varphi Y}{1-(1-\varphi ) Y}},\alpha_{1},\alpha_{2}\right),\;\;\;0\leq Y\leq 1} 따라서, Ω α , ) displaystyle \sim \Gamma (\alpha 1},\theta {1})} Ω α , 2 ) displaystyle \sim \Gamma (\alpha 2},\theta {2})} 경우 Y U V {\displaystyle frac {U}{U+V}}} Y (Y {\displaystyle f_{Y}(Y,\varphi displaystyle frac theta _{ theta {1}}}
Y의 분포 Y f Y , displaystyle \simf_{Y} Y,\varphi 경우
Θ Y ∼ f Y ( Y , φ , Θ ) {\displaystyle \Theta Y\simf_{Y}(Y,\varphi,\Theta )} 여기 f Y , 1 1 2 1 α , α 2 ), 0 displaystyle f_{Y}(Y,\varphi,\Theta frac {\varphi /\Theta 1-(1-\varphi) Y/\ 세타]^{2}}\beta \left({\frac {\varphi Y/\Theta }{1-(1-\varphi)Y/\ Theta }},\alpha _{1},\alpha _{2}\right),\;\;\;0\leq Y\leq \Theta }
θ Y {\displaystyle Theta Y } θ U φ {\displaystyle Theta U}{U+\varphi V}} 베타분포 표본의 역수 두 변수의 비율 분포는 아니지만 한 변수에 대해 다음과 같은 항등식이 유용합니다.
만약 X β α ) displaystyle X\sim (\alpha,\lapha x X β ' β displaystyle mathbf {x} frac {X}{1-X}\sim '(\alpha,\lapha )} Y α , displaystyle \mathbf {Y} sim \lambf '(\alpha,\alpha )'} 1 Y ′ β , α displaystyle frac {1}{\mathbf {Y}}\sim \lambf '(\lambf,\alpha 뒤의 두 방정식의 산출량을 합하면
만약 X β α ) displaystyle X\sim (\alpha,\alpha )} 1 X 1 ' β , α displaystyle \mathbf {x} frac {1}{X}-1\sim \display'(\displaystyle,\alpha 만약 Y β α ) {\displaystyle \mathbf } \sim alpha,\ , y Y Y β α , β displaystyle frac mathbf {Y}}{1+\mathbf {Y}}\sim \lament (\alpha,\lament )} since 11 Y 1 Y 1 1 β β , α displaystyle frac {1}{1+\mathbf {Y}}} {\frac mathbf {Y}^{-1}}{\mathbf {Y}^{-1}+1}}\sim \sim (\sim,\alpha
그리고나서
1 Y ββ , α ) } displaystyle +\mathbf {Y} sim \{\;\beta (\beta,\alpha )\;\}^{-1 β , α {\displaystyle \beta (\beta,\alpha 샘플 U Ω α , 1 Ω β , 1 displaystyle sim \Gamma (\alpha, 1 V\sim \Gamma (\beta, 1)} UV ' α , β displaystyle frac {U}{V}}\sim \beta alpha,\beta
U / V 1 + U / V = U V + U ∼ β ( α , β ) {\displaystyle {\frac {U/V}{1+U/V}}={\frac {U}{V+U}}\sim \sim \sim (\alpha,\sim )} 추가 결과는 역분포 기사 에서 확인할 수 있습니다.
X, Y {\displaystyle ,\;Y} 평균 μ를 갖는 독립 지수 랜덤 변수 라면 X - Y는 평균이 0 이고 척도 μ를 갖는 이중 지수 랜덤 변수입니다. 이항 분포 이 결과는 1978년 [20]
X ~ 이항식 n , p1 ) displaystyle \sim text{이항식}}( n ,p_{1})} 이항식 m , p2 ) displaystyle \sim text{이항식}(m,p_{2})} {\displaystyle }, {\displaystyle } 가정 T = n m {\displaystyle frac {X/n}{Y/m 합니다
로그 T displaystyle \log(T)} 로그 p 1 p 2 {\displaystyle \log(p_{1}/p_{2})}, 1 p 1 1 n frac p_{1})}, n}, frac p_{2})}, {{m
이항 비율 분포는 임상 시험에서 중요한 의미를 갖습니다. 만약 T 의 분포가 위와 같이 알려진다면, 주어진 비율이 순전히 우연에 의해 발생할 확률, 즉 거짓 양성 시험을 추정할 수 있습니다. 여러 논문에서 이항 [citation needed 비율에 대한 여러 근사치의 강건성을 비교합니다.
포아송 분포 및 절단된 포아송 분포 포아송 변수 R = X/Y 의 비율에서는 Y가 유한 확률로 0 이므로 R이 정의되지 않는 문제 가 있습니다. 이에 대응하기 위해 Y 의 0개 표본이 할인되는 절단되거나 검열된 비율 R' = X/Y' 를 고려합니다. 또한 많은 의료 유형의 조사에서 X와 Y 모두의 0 표본의 신뢰성에 체계적인 문제가 있으며 어쨌든 0 표본을 무시하는 것이 좋은 방법일 수 있습니다.
귀무 포아송 표본이 e {\displaystyle ^{-\lambda
p ~ x ( x ; λ ) = 1 1 − e − λ e − λ λ x x ! , x ∈ 1 , 2 , 3 , ⋯ {\displaystyle {\tilde {p}}_{x}(x;\cdots)={\frac {1}{1-e^{-\cdots}}{\frac {e^{-\cdots}}{\cdots}}{\frac {e^{-\cdots}}{\cdots}},\;\;x\in 1,2,3,\cdots} 하나가 되는 거죠 Cohen에 [21] 다차원 절단 pdf는
p ~ ( x 1 , x 2 , … , x n ; λ ) = 1 ( 1 − e − λ ) n ∏ i = 1 n e − λ λ x i x i ! , x i ∈ 1 , 2 , 3 , ⋯ {\displaystyle {\tilde {p}}(x_{1},x_{2},\display)={\frac {1}{(1-e^{-\display})^{n}}\displaystyle {\displaystyle {\display}}\displaystyle {\display}{\displaystyle {\tilde {p}}\displaystyle {x_{i}{x_{i}}{x_{i}}{x_{i}! }},\;\;\;x_{i}\in 1,2,3,\cdots } 그리고 로그 가능성은
L = ln ( p ~ ) = − n ln ( 1 − e − λ ) − n λ + ln ( λ ) ∑ 1 n x i − ln ∏ 1 n ( x i ! ) , x i ∈ 1 , 2 , 3 , ⋯ {\displaystyle L=\ln({\tilde {p}})=-n\ln(1-e^{-\cdots})-n\cdots +\n(\cdots)\sum _{1}^{n}x_{i}-\n\cdots _{1}^{n}(x_{i}!),\;\;x_{i}\in 1,2,3,\cdots } 차별화를 통해 우리는
d L / d λ = − n 1 − e − λ + 1 λ ∑ i = 1 n x i {\displaystyle dL/d\lambda = {\frac {-n}{1-e^{-\lambda}}+{\frac {1}{\lambda}}\sum _{i=1}^{n}x_{i}} 그리고 0으로 설정하면 최대 우도 추정치 λ ^ ML displaystyle hat lambda}}_{ML}
λ ^ M L 1 − e − λ ^ M L = 1 n ∑ i = 1 n x i = x ¯ {\displaystyle {\frac {\hat {\n}}_{ML}}{1-e^{-{\hat {\n}}_{ML}}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\bar {x}}} λ 0 {\displaystyle {\hat {\display}}\to } 1 displaystyle bar {x}}\to {\displaystyle \display} 는 잘린 평균 x {\displaystyle bar {x}} 값 그러나 λ i 일반적인 포아송 분포의 방법론을 사용하여 t.
닫힌 형식 솔루션이 없는 경우 절단 {\displaystyle lambda} 전체 ≤ x ≤ displaystyle \leq \lambda \infty ;\;1\leq bar {x}}\leq \infty }
λ ^ = x ¯ − e − ( x ¯ − 1 ) − 0.07 ( x ¯ − 1 ) e − 0.666 ( x ¯ − 1 ) + ϵ , ϵ < 0.006 {\displaystyle {\hat {\display}}={\bar {x}}-e^{-({\bar {x}}-1)-0.07({\bar {x}-1)e^{-0.666({\bar {x}-1)}+\epsilon,\;\;\epsilon <0.006} 단순히 λ ^ x displaystyle hat {\bar {x 비율 ^ displaystyle {\ display}}_{X}/{\ display}}_ Y }} λ {\displaystyle {\hat lambda}} λ ^ Y {\displaystyle hat lambda}}_{ Y}}
λ ^ {\displaystyle n\lambda {\text{variance }}(및 크라메르-라오 경계 )의 점근적 큰 n λ 분산은
V a r ( λ ^ ) ≥ − ( E [ δ 2 L δ λ 2 ] λ = λ ^ ) − 1 {\displaystyle \mathbb {Var}({\hat {\mathbb}})\geq -\left(\mathbb {E} \left[{\frac {\frac ^{2}L}{\delta ^{2}}\right]_{\delta ={\hat {\delta}}\right)^{-1} L로 대체 하면 다음과 같이 주어집니다.
δ 2 L δ λ 2 = − n [ x ¯ λ 2 − e − λ ( 1 − e − λ ) 2 ] {\displaystyle {\frac {\bar ^{2}}{\delta \delta ^{2}}=-n\left[{\frac {\bar {x}}{\bar ^{2}}}-{\frac {e^{-\bar }}}{{(1-e^{-\bar })^{{2}}\right]}} 위의 식에서 x {\ displaystyle bar {x}} 대입
V a r ( λ ^ ) ≥ λ ^ n ( 1 − e − λ ^ ) 2 1 − ( λ ^ + 1 ) e − λ ^ {\displaystyle \mathbb {Var}({\hat {\lambda}})\geq {\frac {\hat {\lambda}}{n}}{\frac {(1-e^{-{\hat {\lambda}})^{2}}{{\hat {\lambda}}}^{-({\hat {\lambda}}}} n번의 시행을 기준 으로 평균 λ {\displaystyle \lambda 따라 0으로 점증적으로 감소합니다. 작은 displaystyle \lambda }
V a r ( λ ) = λ / n 1 − e − λ [ 1 − λ e − λ 1 − e − λ ] {\displaystyle \mathbb {Var}(\displaystyle)={\frac {\display/n}{1-e^{-\display}}\left[1-{\frac {\displaye^{-\display}}}{1-e^{-\display}}\right]} 이 섹션의 맨 위에 표시된 왼쪽 상단 pdf의 n 샘플에 대해 . Cohen은 pdf, Var Var {\displaystyle \mathbb {Var}({\hat {\lambda}})/\mathbb {Var}(\lambda displaystyle \lambda}( {\displaystyle lambda}
이러한 평균 및 분산 모수 추정치는 X에 대한 병렬 추정치와 함께 포아송 비율에 대한 정규 또는 이항 근사치에 적용할 수 있습니다. 시험 표본은 포아송 과정에 적합하지 않을 수 있습니다. 포아송 절단에 대한 추가적인 논의는 Dietz and Bohning에[23] 0개 의 포아송 분포 위키백과 항목이 있습니다.
이중 로맥스 분포 이 분포는 두 개 의 [24] 분포 의 비율입니다. X 와 Y를 표준 라플라스에 동일한 분포된 랜덤 변수라고 하고 z = X / Y 라고 합니다 .그러면 z 의 확률분포는
f ( x ) = 1 2 ( 1 + z ) 2 {\displaystyle f(x)={\frac {1}{2(1+ z)^{2}}}} X 및 Ya의 평균을 그대로 두십시오.그런 다음 표준 이중 로맥스 분포는 a를 중심 으로 대칭됩니다.
이 분포에는 무한 평균과 분산이 있습니다.
Z 에 표준 이중 로맥스 분포가 있으면 1/Z 에도 표준 이중 로맥스 분포가 있습니다.
표준 Lomax 분포는 단일 분포이며 Laplace 분포보다 꼬리가 더 무겁습니다.
0 < a < 1의 경우 a번째 모멘트가 존재합니다.
E ( Z a ) = Γ ( 1 + a ) Γ ( 1 − a ) {\displaystyle E(Z^{a})={\frac {\Gamma(1+a)}{\ 감마 (1-a)}} 여기서 Δ는 감마 함수입니다.
다변량 분석에서의 비율 분포 비율 분포는 다변량 [25] 랜덤 행렬 X 와 Y가 Wishart 분포 를 따르는 경우, 행렬식 의 비율
φ = X / Y {\displaystyle \varphi = \mathbf {X} / \mathbf {Y} } 는 독립적 인 F 랜덤 변수의 곱에 비례합니다. X 와 Y가 독립적으로 표준화된 Wishart 분포에서 나온 경우 , 비율
Λ = X / X + Y {\displaystyle \Lambda = { \mathbf {X} / \mathbf {X} +\mathbf {Y}}} 윌크스의 람다 분포를 가지고 있습니다
Wishart 행렬이 포함된 2차 형태의 비율 확률 분포는 무작위 이차 형식에서 유도될 수 있습니다.
r = V T A V {\displaystyle r=V^{T}AV} 여기 {\displaystyle } 또는 displaystyle } [26] A 가 다른 행렬 B의 역이면 r V 1 V displaystyle V^{T}B^{-1}V}
가우시안 경우, A 가 복소수 Wishart 분포 W C A , k p {\ displaystyle \sim {C}(A_{0}, k p)} 차원성 p x p 및 k 자유도 {\displaystyle \geq 반면 displaystyle } (. H (.^{H }} ,
r = k V H A 0 − 1 V V H A − 1 V {\displaystyle r=k{\frac {V^{H}A_{0}^{-1}V}{V^{H}A^{-1}V}} Gamma 분포를 따릅니다.
p 1 ( r ) = r k − p e − r Γ ( k − p + 1 ) , r ≥ 0 {\displaystyle p_{1}(r)={\frac {r^{k-p}e^{-r}}{\Gamma(k-p+1)},\;\;r\geq 0} 결과는 최소 제곱 적응형 위너 필터링에서 발생합니다. 의 [25] 원래 기사에서는 분포 p r k p r Ω k p displaystyle p_{1}(r r^{k-p-1}\;e^{-r}\;/\Gamma(k-p
마찬가지로, 전체 순위 (k p displaystyle \geq 샘플 W Ω k p displaystyle sim (\Sigma,k,p 및 W와 무관 한 V 랜덤 벡터에 대하여, 비율
r = V T Σ − 1 V V T W − 1 V ∼ χ k − p + 1 2 {\displaystyle r={\frac {V^{T}\Sigma ^{-1}V}{V^{T}W^{-1}V}}\sim \chi _{k-p+1}^{2 }} 이 결과는 보통 Muirhead(1982)[27]
주어진 복잡한 Wishart 행렬 WC ( I , k , p ) displaystyle \sim {C}(I,k,p
ρ = ( V H A − 1 V ) 2 V H A − 2 V ⋅ V H V {\displaystyle \rho = {\frac {(V^{H}A^{-1}V)^{2}}{V^{ H}A^{-2}V\cdot V^{H}V}} 베타 분포를 따릅니다(의 eqn(47[28]
p 2 ( ρ ) = ( 1 − ρ ) p − 2 ρ k − p + 1 k ! ( k + 1 − p ) ! ( p − 2 ) ! , 0 ≤ ρ ≤ 1 {\displaystyle p_{2}(\rho)=(1-\rho)^{p-2}\rho^{k-p+1}{\frac {k!}{(k+1-p)!(p-2)! }},\;\;\;0\leq \rho \leq 1} 제한 최소 제곱 필터링의 성능 분석에서 결과가 발생하며, A W C A , n , p ) displaystyle \sim {C} A_{0}, n, p)} 보다
ρ = ( V H A − 1 V ) 2 V H A − 1 A 0 A − 1 V ⋅ V H A 0 − 1 V {\displaystyle \rho = {\frac {(V^{H}A^{-1}V)^{2}}{V^{ H}A^{-1}A_{0}A^{-1}V\cdot V^{H}A_{0}^{-1}V}} 가장 간단한 형태로, 만약 Ai j W I , k , displaystyle A_{i, sim W_{C} (I,k, Wi, j W 1 j displaystyle W^{ left(W^{-1}\right)_{i,j}
ρ = ( W 1 , 1 ) 2 ∑ j ∈ 1.. p W 1 , j 2 ∼ β ( p − 1 , k − p + 2 ) {\displaystyle \rho = {\frac {\left(W^{1,1}\right)^{2}}{\sum _{j\in 1.. p} W^{1,j} ^{2}}\sim \beta (p-1,k-p+2)} 참고 항목 메모들 ^ 그러나 X 1 displaystyle {1}} 및 X displaystyle X_{2}} 로그 정규 분포를 나타낼 수 있습니다 2022-06-08년 현재 "코풀라(확률 이론)" 에 대한 위키피디아 기사에는 Gumbel 코풀라와 두 개의 정규 한계 관절의 밀도와 윤곽도가 포함되어 있으며, 여기서 관절 분포는 이변량 정규 분포가 아닙니다. 참고문헌 ^ a b Geary, R. C. (1930). "The Frequency Distribution of the Quotient of Two Normal Variates". Journal of the Royal Statistical Society 93 (3): 442–446. doi :10.2307/2342070 . JSTOR 2342070 .^ Fieller, E. C. (November 1932). "The Distribution of the Index in a Normal Bivariate Population". Biometrika 24 (3/4): 428–440. doi :10.2307/2331976 . JSTOR 2331976 . ^ a b Curtiss, J. H. (December 1941). "On the Distribution of the Quotient of Two Chance Variables" . The Annals of Mathematical Statistics 12 (4): 409–421. doi :10.1214/aoms/1177731679 JSTOR 2235953 . ^ 조지 마르살리아 (1964년 4월).정규 변수의 비율 균일 변수의 합계의 비율 국방기술정보센터입니다 ^ Marsaglia, George (March 1965). "Ratios of Normal Variables and Ratios of Sums of Uniform Variables" . Journal of the American Statistical Association 60 (309): 193–204. doi :10.2307/2283145 . JSTOR 2283145 . Archived from the original on September 23, 2017.^ a b c Hinkley, D. V. (December 1969). "On the Ratio of Two Correlated Normal Random Variables". Biometrika 56 (3): 635–639. doi :10.2307/2334671 . JSTOR 2334671 .^ a b Hayya, Jack ; Armstrong, Donald; Gressis, Nicolas (July 1975). "A Note on the Ratio of Two Normally Distributed Variables". Management Science 21 (11): 1338–1341. doi :10.1287/mnsc.21.11.1338 . JSTOR 2629897 .^ a b c d e f Springer, Melvin Dale (1979). The Algebra of Random Variables Wiley . ISBN 0-471-01406-0 ^ a b Pham-Gia, T.; Turkkan, N.; Marchand, E. (2006). "Density of the Ratio of Two Normal Random Variables and Applications". Communications in Statistics – Theory and Methods . Taylor & Francis . 35 (9): 1569–1591. doi :10.1080/03610920600683689 . S2CID 120891296 . ^ Brody, James P.; Williams, Brian A.; Wold, Barbara J.; Quake, Stephen R. (October 2002). "Significance and statistical errors in the analysis of DNA microarray data" (PDF) . Proc Natl Acad Sci U S A 99 (20): 12975–12978. Bibcode :2002PNAS...9912975B . doi :10.1073/pnas.162468199 PMC 130571 PMID 12235357 . ^ Šimon, Ján; Ftorek, Branislav (2022-09-15). "Basic Statistical Properties of the Knot Efficiency" . Symmetry . MDPI. 14 (9): 1926. doi :10.3390/sym14091926 ISSN 2073-8994 . ^ Díaz-Francés, Eloísa; Rubio, Francisco J. (2012-01-24). "On the existence of a normal approximation to the distribution of the ratio of two independent normal random variables". Statistical Papers . Springer Science and Business Media LLC. 54 (2): 309–323. doi :10.1007/s00362-012-0429-2 . ISSN 0932-5026 . S2CID 122038290 . ^ Baxley, R T; Waldenhorst, B T; Acosta-Marum, G (2010). "Complex Gaussian Ratio Distribution with Applications for Error Rate Calculation in Fading Channels with Imperfect CSI" . 2010 IEEE Global Telecommunications Conference GLOBECOM 2010 . pp. 1–5. doi :10.1109/GLOCOM.2010.5683407 . ISBN 978-1-4244-5636-9 S2CID 14100052 . ^ Sourisseau, M.; Wu, H.-T.; Zhou, Z. (October 2022). "Asymptotic analysis of synchrosqueezing transform—toward statistical inference with nonlinear-type time-frequency analysis" . Annals of Statistics . 50 (5): 2694–2712. doi :10.1214/22-AOS2203 . ^ 물론 중심 극한 정리의 모든 호출은 유한 분산과 같은 적합하고 일반적으로 충족되는 규칙성 조건을 가정합니다. ^ a b c Kermond, John (2010). "An Introduction to the Algebra of Random Variables". Mathematical Association of Victoria 47th Annual Conference Proceedings – New Curriculum. New Opportunities . The Mathematical Association of Victoria: 1–16. ISBN 978-1-876949-50-1 ^ "SLAPPF" . Statistical Engineering Division, National Institute of Science and Technology. Retrieved 2009-07-02 .^ Hamedani, G. G. (Oct 2013). "Characterizations of Distribution of Ratio of Rayleigh Random Variables". Pakistan Journal of Statistics . 29 (4): 369–376. ^ Raja Rao, B.; Garg., M. L. (1969). "A note on the generalized (positive) Cauchy distribution" . Canadian Mathematical Bulletin 12 (6): 865–868. doi :10.4153/CMB-1969-114-2 ^ Katz D. et al.(1978) 코호트 연구에서 위험 비율에 대한 신뢰 구간 획득 생체 인식 34:469-474 ^ Cohen, A Clifford (June 1960). "Estimating the Parameter in a Conditional Poisson Distribution". Biometrics . 60 (2): 203–211. doi :10.2307/2527552 . JSTOR 2527552 . ^ Springael, Johan (2006). "On the sum of independent zero-truncated Poisson random variables" (PDF) . University of Antwerp, Faculty of Business and Economics . ^ Dietz, Ekkehart; Bohning, Dankmar (2000). "On Estimation of the Poisson Parameter in Zero-Modified Poisson Models". Computational Statistics & Data Analysis . 34 (4): 441–459. doi :10.1016/S0167-9473(99)00111-5 . ^ Bindu P and Sangita K (2015) Double Lomax 분포 및 그 응용 통계 LXXV (3) 331–342 ^ a b Brennan, L E; Reed, I S (January 1982). "An Adaptive Array Signal Processing Algorithm for Communications". IEEE Transactions on Aerospace and Electronic Systems . AES-18 No 1: 124–130. Bibcode :1982ITAES..18..124B . doi :10.1109/TAES.1982.309212 . S2CID 45721922 . ^ Mathai, A M; Provost, L (1992). Quadratic Forms in Random Variables ISBN 0-8247-8691-2 ^ Muirhead, Robb (1982). Aspects of Multivariate Statistical Theory . USA: Wiley. pp. 96, Theorem 3.2.12. ^ Reed, I S; Mallett, J D; Brennan, L E (November 1974). "Rapid Convergence Rate in Adaptive Arrays". IEEE Transactions on Aerospace and Electronic Systems . AES-10 No.6 (6): 853–863. Bibcode :1974ITAES..10..853R . doi :10.1109/TAES.1974.307893 . S2CID 51664535 .
외부 링크 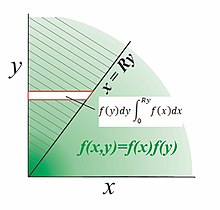










 (를)
(를) 
![{\displaystyle f_{R}(R)={\frac {d}{dR}}\left[\int _{0}^{\infty }f_{y}(y)\left(\int _{0}^{Ry}f_{x}(x)dx\right)dy\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/692b61ad3c87cd15d2b1aa11783adcc25deb0fb2)







![{\displaystyle \operatorname {E} [(UV)^{p}]=\operatorname {E} [U^{p}]\;\;\operatorname {E} [V^{p}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9149cfa34e27efa89667271f15f27fac5697b7dd)
 (가) 독립적인
(가) 독립적인 
 모멘트를 따로 정할 수 있다면
모멘트를 따로 정할 수 있다면 모멘트를 찾을 수 있습니다.Y
모멘트를 찾을 수 있습니다.Y



 .
.
 사용하는 역 Gamma 분포에서 샘플링되었으며, pdf
사용하는 역 Gamma 분포에서 샘플링되었으며, pdf
![{\displaystyle \operatorname {E} [Z^{p}]=\operatorname {E} [Y^{-p}]={\frac {\Gamma (\beta -p)}{\Gamma (\beta )}},\;p<\beta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/183100f28d21720a9011434eef53b9547324ef47)
![{\displaystyle \operatorname {E} [(X/Y)^{p}]=\operatorname {E} [X^{p}]\;\operatorname {E} [Y^{-p}]={\frac {\Gamma (\alpha +p)}{\Gamma (\alpha )}}{\frac {\Gamma (\beta -p)}{\Gamma (\beta )}},\;p<\beta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c849e320d085f73f456cbe534de3cd5f86cbf83)


![{\displaystyle {\begin{aligned}\operatorname {Var} (X/Y)&=\operatorname {E} ([X/Y]^{2})-\operatorname {E^{2}} (X/Y)\\&=\operatorname {E} (X^{2})\operatorname {E} (1/Y^{2})-\operatorname {E} ^{2}(X)\operatorname {E} ^{2}(1/Y)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a0f882624693351c91d81e4e9c4bfb12fa1bdb2)







![p_{Z}(z)={\frac {b(z)\cdot d(z)}{a^{3}(z)}}{\frac {1}{{\sqrt {2\pi }}\sigma _{x}\sigma _{y}}}\left[\Phi \left({\frac {b(z)}{a(z)}}\right)-\Phi \left(-{\frac {b(z)}{a(z)}}\right)\right]+{\frac {1}{a^{2}(z)\cdot \pi \sigma _{x}\sigma _{y}}}e^{{-{\frac {c}{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef0b4fa30467d39da33345eab941c44232fca5f4)






![{\displaystyle p_{Z}^{\dagger }(z)={\frac {1}{\sqrt {\pi }}}{\frac {p}{\mathrm {erf} [q]}}{\frac {1}{r}}{\frac {1+{\frac {p^{2}}{q^{2}}}{\frac {z}{r}}}{\left(1+{\frac {p^{2}}{q^{2}}}\left[{\frac {z}{r}}\right]^{2}\right)^{\frac {3}{2}}}}e^{-{\frac {p^{2}\left({\frac {z}{r}}-1\right)^{2}}{1+{\frac {p^{2}}{q^{2}}}\left[{\frac {z}{r}}\right]^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/760ef876570625a8e20783d35a0a77d275a0dd4c)







 가우스에 가까운 형태로 변환되는 방법을 보여주고 음의 분모
가우스에 가까운 형태로 변환되는 방법을 보여주고 음의 분모 









![{\displaystyle x/y\in [r,r+\delta ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704f8600b0cdc241fbe2ba308a02114da721ea16)
 (가) 0으로 갈수록
(가) 0으로 갈수록 

 에르미트의 전치이고
에르미트의 전치이고















![{\displaystyle p_{Z}(z)={\begin{cases}\left[\varphi (0)-\varphi (z)\right]/z^{2}\quad &z\neq 0\\\varphi (0)/2\quad &z=0,\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498e4c4f1b1dc7cef7b95dd72db44fa7117fa41a)

 분포
분포 베타 소수
베타 소수






![{\displaystyle {\frac {U}{V}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\frac {\theta _{1}}{\theta _{2}}})\quad {\text{ and }}\operatorname {E} \left[{\frac {U}{V}}\right]={\frac {\theta _{1}}{\theta _{2}}}{\frac {\alpha _{1}}{\alpha _{2}-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/191d3f44ba22b870d622d6f4736e5c49f63f7ece)










![{\displaystyle f_{Y}(Y,\varphi )={\frac {\varphi }{[1-(1-\varphi )Y]^{2}}}\beta \left({\frac {\varphi Y}{1-(1-\varphi )Y}},\alpha _{1},\alpha _{2}\right),\;\;\;0\leq Y\leq 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3633e7b73fced71d45789e7f4c5339fbb89ab990)


![{\displaystyle f_{Y}(Y,\varphi ,\Theta )={\frac {\varphi /\Theta }{[1-(1-\varphi )Y/\Theta ]^{2}}}\beta \left({\frac {\varphi Y/\Theta }{1-(1-\varphi )Y/\Theta }},\alpha _{1},\alpha _{2}\right),\;\;\;0\leq Y\leq \Theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/69d2227af45c98a5fe264bacbd94b8119e6728d7)

 역수 분포.
역수 분포. 경우
경우 

 평균 μ를 갖는 독립 지수 랜덤 변수라면 X - Y는 평균이 0이고 척도 μ를
평균 μ를 갖는 독립 지수 랜덤 변수라면 X - Y는 평균이 0이고 척도 μ를 







 왼쪽으로 꺾인 것이 있습니다.
왼쪽으로 꺾인 것이 있습니다.![{\displaystyle \mathbb {Var} ({\hat {\lambda }})\geq -\left(\mathbb {E} \left[{\frac {\delta ^{2}L}{\delta \lambda ^{2}}}\right]_{\lambda ={\hat {\lambda }}}\right)^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48c158b23e75d9fda80844a9340b3de19e20a75d)
![{\displaystyle {\frac {\delta ^{2}L}{\delta \lambda ^{2}}}=-n\left[{\frac {\bar {x}}{\lambda ^{2}}}-{\frac {e^{-\lambda }}{(1-e^{-\lambda })^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25d08fb02fe61e2bc49dfc51bacefce9a92533b0)


![{\displaystyle \mathbb {Var} (\lambda )={\frac {\lambda /n}{1-e^{-\lambda }}}\left[1-{\frac {\lambda e^{-\lambda }}{1-e^{-\lambda }}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67d5b4a7490a4da12f5d1e255df20fdc384d95fd)






 (
( 차원성 p x p 및 k 자유도
차원성 p x p 및 k 자유도 







 경우
경우 



