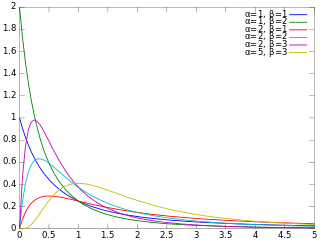
베타 프라임

확률밀도함수
누적분포함수
매개변수	> ${\displaystyle \alpha >0}$ 모양(실제) > ${\displaystyle \property >0}$ 모양(실제)
지원	$[0,\flashstyle x\in [0,\infully )\!}$
PDF	${\displaystyle f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}}{B(\alpha,\beta )}}}\!}$
CDF	${\displaystyle I_{}}$ ${\displaystyle {x\frac{}{}}_{}}$ ${\displaystyle {\frac{1\mathrm{}}{}}_{}}$+ x ${\displaystyle {\frac{}{}\alpha }_{}}$ ,${\displaystyle {\beta }_{}}$) ${\$ 여기서$$ $I{\displaystyle {}_{}}$ ${\displaystyle x_{}}$(${\displaystyle \alpha }$, ${\displaystyle \beta }$) ${\displaystyle I_{x}(\alpha ,\beta )}}$은 불완전한 베타 함수다$$.
평균	${\displaystyle {\frac {\properties}{\reason -1}{\text{{{}\reason >1}$
모드	${\displaystyle {\frac {\frac -1}{\reason +1}{\text{}}}}{}\reason \reason \geq 1{\text{, 0}}$
분산	${\displaystyle {\frac {\frac(\properties +\properties -1)}{{2}}:{{}\text}{{{}}{}\property >2}}:$
왜도	${\displaystyle {\frac {2\buffer +\buffer -1)}{\buffer -3}{\sqrt {\frac {\buffer -2}{\buffer (\buffer -1)}{\text{}}}}}}}}}}$
MGF	${\displaystyle {\frac {e^{-t}\감마(\alpha +\beta )}{{1,2}^{\,2,0}\!\왼쪽(\왼쪽)\\cHB\\\cHB\\\\\\\\nd{nd}\\\\오른쪽 \,-t\오른쪽)}$

확률 이론과 통계에서 베타 프라임 분포(두 번째 종류의^[1] 역전 베타 분포 또는 베타 분포라고도 한다)는 절대적으로 연속적인 확률 분포다.null

정의들

베타 프라임 분포는 α와 β 두 개의 매개변수를 가진 > ${\displaystyle x>0}$에 대해 정의되며 확률밀도함수는 다음과 같다.

${\displaystyle f(x)={\frac {x^{\alpha -1}(1+x)^{-\alpha -\beta }}{B(\alpha ,\beta )}}}$

여기서 B는 베타 함수다.null

누적분포함수는

$F(x;\alpha ,\beta )=I_{\frac {x}{1+x}\왼쪽(\알파,\베타 \오른쪽),}$

여기서 나는 정규화된 불완전한 베타 함수다.null

분포의 예상 값, 분산 및 기타 세부 정보가 사이드 박스에 제공되며, > ${\displaystyle \beta >4}$의 경우 초과 첨도는 다음과 같다.

${\displaystyle \property_{2}=6{\frac {\fract (\buffer -11)+(\buffer -1)^{2}(\buffer -1){\buffer (\buffer -1)(\buffects -3)(\buffer -4)}}}.}$

관련 베타 분포는 확률로 표현되는 베르누이 분포의 모수의 결합 사전 분포인 반면, 베타 프라임 분포는 불화로 표현되는 베르누이 분포의 모수의 결합 사전 분포인 것이다.분포는 Pearson 유형 VI 분포다.^[1]null

만약β 1{\displaystyle \beta 1}(만약 β ≤ 1{\di 변량 X의 최빈 값β′(α, β){\displaystyle \beta '(\alpha ,\beta)}는 X^)α − 1β+1{\displaystyle{\hat{X}}={\frac{\alpha)}{\beta+1}}}. 그것의 평균은αβ − 1{\displaystyle{\frac{\alpha}{\beta)}}}를 나누어 주었다.splays$tyle \beta \leq 1}$ the mean is infinite, in other words it has no well defined mean) and its variance is ${\displaystyle {\frac {\alpha (\alpha +\beta -1)}{(\beta -2)(\beta -1)^{2}}}}$ if ${\displaystyle \beta >2}$.

-< < ${\displaystyle$ -$\alpha <k<\beta }}$의 경우 k-th $순간{\displaystyle }$ E${\displaystyle }$[ ${\displaystyle X^{}}$ k${\displaystyle {}^{}}$]$${\$displaystyle E[X^{k}]}}$은(는) 다음을 통해 주어진다$$.

${\displaystyle E[X^{k}]={\frac {B(\alpha +k,\beta -k)}{B(\alpha ,\beta )}}.}$

N displaystyle k\$in \mathb$ {N$}($k <$β$ , ${\displaystyle k<\beta ,})$의 경우 이렇게 하면 다음과 같이 간단해진다.

${\displaystyle E[X^{k}]=\prod _{i=1}^{k}{\frac {\alpha +i-1}{\beta -i}}}.}$

cdf는 또한 다음과 같이 쓸 수 있다.

${\displaystyle {\x^{\alpha }\cdot {}_{2}F_{1}(\alpha +\alpha +\alpha +1,-x)}{\alpha \cdot B(\alpha ,\beta )}}}$

여기서 ${\displaystyle {}_{\mathrm{}}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$1}은$$(는) 가우스의 초기하 함수 F이다₁.

대체 매개 변수화

베타 프라임 분포는 평균 μ > 0 및 정밀도 μ > 0 매개변수(^[2] 페이지 36)의 관점에서 재평가될 수 있다.null

파라메타화 μ/(β-1) 및 μ = β-2, 즉 α = μ(1 + μ) 및 β = 2 + μ. 이 파라미터화 하에서는 E[Y] = μ, Var[Y] = μ(1 + μ)/μs를 고려한다.null

일반화

일반화된 베타 프라임 분포 $\beta {\displaystyle {}^{}}$ ${\displaystyle \prime }$ (${\displaystyle \alpha }$, ${\displaystyle \beta }$, p ,${\displaystyle q}$) ${\displaystyle \beta '(\alpha ,\beta ,p,q)}$을 형성하기 위해 두 개의 파라미터를 더 추가할 수 있다$.$

• > ${\displaystyle p>0}$ 모양(실제)
• > ${\displaystyle q>0}$척도(실제)

확률밀도함수:

${\displaystyle f(x;\alpha ,\beta ,p,q)={\frac {p\left({\frac {x}{q}}\right)^{\alpha p-1}\left(1+\left({\frac {x}{q}}\right)^{p}\right)^{-\alpha -\beta }}{qB(\alpha ,\beta )}}}$

비열하게

${\displaystyle {\frac {q\Gamma \left(\alpha +{\tfrac {1}{p}\오른쪽)\감마(\beta -{\tfrac {1}{p}})}{\감마(\alpha )\감마(\beta )}}}\quad{\text{}}}}}\beta p>1}$

및 모드

${\displaystyle q\lefted\frac {\reft p-1}{\p+1}\오른쪽)^{\tfrac {1}{p}\p}\reason{\text{}}}\reason p\geq 1}$

p = q = 1이면 일반화된 베타 프라임 분포가 표준 베타 프라임 분포로 감소한다는 점에 유의하십시오.

복합 감마 분포

복합 감마 분포는^[3] 척도 모수인 q를 추가할 때 베타 프라임의 일반화지만 여기서 p = 1이다.다음과 같은 두 개의 감마 분포를 혼합하여 형성되기 때문에 이렇게 이름이 붙여진다.

${\displaystyle \beta '(x;\alpha ,\beta ,1,q)=\int _{0^{0}{\infit }G(x;\alpha ,r)G(r;\beta ,q)\;dr}$

여기서 G(x;a,b)는 형상 a와 역 척도 b를 갖는 감마 분포다.이 관계는 복합 감마 또는 베타 프라임 분포를 갖는 랜덤 변수를 생성하는 데 사용될 수 있다.null

복합 감마의 모드, 평균 및 분산은 위의 infobox의 모드와 평균에 q를 곱하고 분산을 q를² 곱하여 얻을 수 있다.

특성.

• $X{\displaystyle }$ ~${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$(${\displaystyle \alpha }$ ,${\displaystyle \beta }$) ${\displaystyle X\sim \beta '(\alpha ,\beta )}$인 경우 ${\displaystyle \frac{1}{}}$ $X{\displaystyle \frac{\mathrm{}}{}}$ ~${\displaystyle {}^{}}$ ′${\displaystyle {}^{}}$(${\displaystyle \alpha }$ $){\$tfrac {$1}{X}\displaystyle {\tfrac$ {1$}\beta ,\alpha$ $)\}.$
• $X{\displaystyle }$ ~${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$(${\displaystyle \alpha }$ ,${\displaystyle \beta }$, ${\displaystyle p}$ ,${\displaystyle q}$) ${\displaystyle$ X$\sim \beta '(\alpha ,\beta ,p,q)}$이면 K ${\displaystyle X}$~ β ${\displaystyle {}^{}(}$α${\displaystyle }$, ${\displaystyle \beta }$, ${\displaystyle p}$,$$ ) $displaysty kX\sim \bta '(\alpha$ ,$beta$ ,p,\beta,$p$,p,p,$kq$
• ${\displaystyle \cHB '(\displaystyle \properties,\filense,1,1)=\display '(\displaysty$
• If ${\displaystyle X_{1}\sim \beta '(\alpha ,\beta )}$ and ${\displaystyle X_{2}\sim \beta '(\alpha ,\beta )}$ two iid variables, then ${\displaystyle Y=X_{1}+X_{2}\sim \beta '(\gamma ,\delta )}$ with ${\displaystyle \gamma =\frac{2\alpha (\alpha +{\beta }^2-2\beta +2}{}}$${\displaystyle \gamma ={\frac {2\alpha (\alpha +\beta ^{2}-2\beta +2\alpha \beta -4\alpha +1)}{(\beta -1)(\alpha +\beta -1)}}}$ and ${\displaystyle \delta ={\frac {2\alpha +\beta ^{2}-\beta +2\alpha \beta -4\alpha }{\alpha +\beta -1}}}$, as t그의 베타 프라임 분포는 무한히 분리될 수 있다.
• More generally, let ${\displaystyle X_{1},...,X_{n}n}$ iid variables following the same beta prime distribution, i.e. ${\displaystyle \forall i,1\leq i\leq n,X_{i}\sim \beta '(\alpha ,\beta )}$, then the sum ${\di$$splaystyle S=X_{1}+...$$+X_{n}\sim \beta '(\gamma ,\delta )}$ with ${\displaystyle \gamma ={\frac {n\alpha (\alpha +\beta ^{2}-2\beta +n\alpha \beta -2n\alpha +1)}{(\beta -1)(\alpha +\beta -1)}}}$ and ${\displaystyle \delta$$={\frac {2\buffer +\buffer ^{2}-\buffer$+\buffer$\n\buffer$ \buffer$\}\{\backslash$$buffer +\buffer -1}.$

관련 분포

• If ${\displaystyle X\sim F(2\alpha ,2\beta )}$ has an F-distribution, then ${\displaystyle {\tfrac {\alpha }{\beta }}X\sim \beta '(\alpha ,\beta )}$, or equivalently, ${\displaystyle X\sim \beta '(\alpha ,\beta ,1,{\tfrac {\beta }{\alpha }})}$.
• $X{\displaystyle }$~ ${\displaystyle \text{베타}(\alpha }$ ,${\displaystyle \beta }$) ${\displaystyle$ X$\sim {\textrm${\$beta}(\alpha ,\beta )}$이면 ${\displaystyle \frac{X\mathrm{}}{}}$ ${\displaystyle \frac{1}{}}$- X ~${\displaystyle \frac{}{}{}^{}}$ ${\displaystyle \prime (\alpha }$, ${\displaystyle \alpha }$) ${\displaystyle {\frac {X}{1-X}}\sim(\alpha ,\beta$ $)\}).$
• If ${\displaystyle X\sim \Gamma (\alpha ,\theta )}$ and ${\displaystyle Y\sim \Gamma (\beta ,\theta )}$ are independent, then ${\displaystyle {\frac {X}{$$Y}\sim \beta '(\alpha,\beta$ $)\}.$
• Parametrization 1: If ${\displaystyle X_{k}\sim \Gamma (\alpha _{k},\theta _{k})}$ are independent, then ${\displaystyle {\tfrac {X_{1}}{X_{2}}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\tfrac {\theta _{1}}{\theta _{2}}})}$.
• Parametrization 2: If ${\displaystyle X_{k}\sim \Gamma (\alpha _{k},\beta _{k})}$ are independent, then ${\displaystyle {\tfrac {X_{1}}{X_{2}}}\sim \beta '(\alpha _{1},\alpha _{2},1,{\tfrac {\beta _{2}}{\beta _{1}}})}$.
• ${\displaystyle {\beta }^{}}$ ${\displaystyle \prime (p,}$ 1,${\displaystyle a,}$ b${\displaystyle }$)${\displaystyle }$= ${\displaystyle \text{Dagum}(p}$, ${\displaystyle a}$ ,${\displaystyle b}$) ${\displaystyle \beta '(p,1,a,b)={\textrm {Dagum}(p,a,b)}}$다금 분포
• ${\displaystyle {\beta }^{}}$ ${\displaystyle {\prime }^{}}$(${\displaystyle 1}$,${\displaystyle p}$, ${\displaystyle a}$ ,${\displaystyle b}$)${\displaystyle }$= ${\displaystyle \text{SinghMaddala}}$(${\displaystyle p}$,${\displaystyle a}$ , b ) ${\displaystyle \beta$'($1,p,a,$b)={\$textrm {SinghMaddala}(p,a,b)}}}$싱-마드달라 분포.
• ${\displaystyle {\beta }^{}}$ ${\displaystyle {\prime }^{}}$(${\displaystyle 1}$, ${\displaystyle 1}$,${\displaystyle \gamma }$ ,${\displaystyle \sigma }$)${\displaystyle }$= ${\displaystyle \text{LL}}$ (${\displaystyle \gamma }$, ${\displaystyle \sigma }$) ${\displaystyle \beta '(1,1,\gamma ,\sigma )={\textrm {LL}(\gamma ,\sigma )}$ 로지스틱 분포.
• 베타 프라임 분포는 타입 6 피어슨 분포의 특별한 경우다.
• X가 최소 $x{\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\$과 형상 매개변수 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$을(를$)$ 가진 파레토 분포를 가지고 있는 경우, $X{\displaystyle {\displaystyle \frac{}{}}}$ ${\displaystyle {\displaystyle \frac{x_{}}{}}}$m -${\displaystyle 1}$ ~ ${\displaystyle \mathrm{\beta }}$ ${\displaystyle {\prime \mathrm{}}^{}}$($1$ ${\displaystyle \alpha }$)$${\$dfrac {x_}{m$}-1}-$1\sim \beta$
• If X has a Lomax distribution, also known as a Pareto Type II distribution, with shape parameter ${\displaystyle \alpha }$ and scale parameter ${\displaystyle \lambda }$, then ${\displaystyle {\frac {X}{\lambda }}\sim \beta ^{\prime }(1,\alpha )}$.
• If X has a standard Pareto Type IV distribution with shape parameter ${\displaystyle \alpha }$ and inequality parameter ${\displaystyle \gamma }$, then ${\displaystyle X^{\frac {1}{\gamma }}\sim \beta ^{\prime }(1,\alpha )}$, or equivalently, ${\display$$스타일 X\sim \beta ^{\premy ^}(1,\alpha ,{\tfrac {1}{\gamma },1)}$.
• 역디리클레 분포는 베타 프라임 분포의 일반화다.

메모들

참조

• 존슨, N.L., 코츠, S., 발라크리쉬난, N.(1995)연속적인 일변량 분포, 제2권(2판), 와일리.ISBN 0-471-58494-0
• Bourguignon, M.; Santos-Neto, M.; de Castro, M. (2021), "A new regression model for positive random variables with skewed and long tail", Metron, 79: 33–55, doi:10.1007/s40300-021-00203-y, S2CID 233534544

• 매스월드 기사