기 분포

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Chi distribution" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2009년 10월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

기를

확률밀도함수
누적분포함수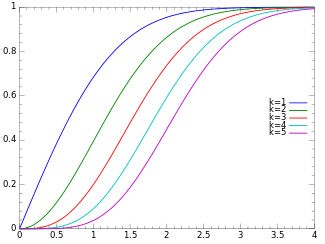
매개변수	> 0 ${\$자유)
지원	$[0,\displaystyle x\in [0,\fty )}$
PDF	${\displaystyle {\frac{1}{2^{(k/2)-1}\감마(k/2}})}\;x^{k-1}e^{-x^{2}/2}}$
CDF	${\displaystyle P(k/2,x^{2}/2)\,}$
평균	${\displaystyle \mu ={\sqrt{2}\,{\frac {\Gamma((k+1)/2)}}{\감마(k/2}})}$
중앙값	${\displaystyle \약 {\sqrt {k{\bigg (}1}1-{\frac {2}{9k}{\bigg )}^{3}}}}}}}}}}}}}}}}}}}}}}}}"$
모드	${\displaystyle \sqrt{}}$$k{\displaystyle }$ -${\displaystyle \sqrt{1}}$ $displaystyle {\sqrt {k-1},$ ${\displaystyle \ge }$ ${\displaystyle 1}$ ${\displaystyle k\geq$ 1$}$의 경우$$
분산	${\displaystyle \sigma ^{2}=k-\mu ^{2}\,}$
왜도	${\displaystyle \property_{1}={\frac {\mu }{\ma ^{3}}\,(1-2\ma ^{2})}$
엑스트라 쿠르토시스	${\displaystyle {\frac {2}{\frac ^{2}}(1-\mu \ \ma \ \ma \gammama \{1}-\sigma ^{2}})$
엔트로피	${\displaystyle \ln(\Gamma(k/2))+\,}$ ${\displaystyle {\frac{1}{2}}(k\!-\\ln(2)\!\(k\!\!1)\properties _{0}(k/2)}$
MGF	복잡하다(텍스트 참조)
CF	복잡하다(텍스트 참조)

확률 이론과 통계에서 기 분포는 연속 확률 분포다. 이것은 각각 표준 정규 분포를 따르는 독립 랜덤 변수 집합의 제곱합에 대한 양의 제곱근의 분포 또는 원점에서 랜덤 변수의 유클리드 거리 분포와 동등하게 분포한다. 따라서 카이-제곱 분포를 따르는 변수의 양의 제곱근 분포를 설명함으로써 카이-제곱 분포와 관련이 있다.

$Z{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle }$… , ${\displaystyle Z_{}}$ k ${\$이(가) $k{\displaystyle }$ ${\displaystyle k}$ 독립적이고$$ 평균 0 및 표준 편차 1인 경우 통계량

${\displaystyle Y={\sqrt {\sum _{i=1}^{k}Z_{i}^{2}}:$

기 분포에 따라 분포한다. 카이 분포에는 자유도(즉, 임의 변수 ${\displaystyle Z_{}}$ i ${\$를 지정하는 $k{\displaystyle }$ ${\displaystyle k$라는 파라미터가 하나 있다.$$

가장 친숙한 예는 이상적인 기체 내 분자 속도의 레일리 분포(자유도 2도의 키 분포)와 맥스웰-볼츠만 분포(자유도 3도의 키 분포)이다.

정의들

확률밀도함수

카이-분포의 확률밀도함수(pdf)는

${\displaystyle f(x;k)={\begin{case}{\dfrac {x^{k-1}/2}}:{2^{x^{2-1}\2}}:\감마 \left({\frac {k}{2}}\오른쪽)}}},&x\geq;\\\ntext{otherwise}.\end{case}}}$

여기서 $\gamma {\displaystyle \mathrm{}}$( ${\displaystyle z}$) ${\displaystyle \Gamma (z)}$은 감마함수다.

누적분포함수

누적분포함수는 다음과 같다.

${\displaystyle F(x;k)=P(k/2,x^{2}/2)\,}$

여기서 $P{\displaystyle (k}$, x${\displaystyle }$) ${\displaystyle P(k,x)}$은 정규화된 감마함수다.

함수 생성

모멘트 생성 기능은 다음과 같이 제공된다.

${\displaystyle M(t)=M\left({\frac {k}{2}},{\frac {1}{1}{1}2}},{\frac {t^{2}}:2}}\\오른쪽)+t{\sqrt{2}}\,{\frac {\Gamma((k+1)/2))}}{\감마(k/2}}:00)}{\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}:\오른쪽),}}$

여기서 $M{\displaystyle (}$ ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle z}$) ${\displaystyle M(a,b,z)}$은 쿠메르의 결합초기하 함수다. 특성 함수는 다음과 같이 주어진다.

${\displaystyle \varphi(t;k)=M\left({\frac {k}{2}},{\frac {1}{1}:{2}}: {\frac {-t^{2}}:2}}\\오른쪽)+it{\sqrt{2}}\,{\frac {\gamma(((k+1)/2))/2)}}{\감마(k/2}}:00)}{\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}:\오른쪽).}$

특성.

순간

그 후, 다음과 같은 순간들이 주어진다.

${\displaystyle \mu _{j}=\int _{0}^{{0}^{f(x;k)x^{j}x=2^{j/2}{\frac {\감마((k+j)/2)}}{\감마(k/2}})}$

여기서 $\gamma {\displaystyle \mathrm{}}$( ${\displaystyle z}$) ${\displaystyle \Gamma (z)}$은 감마함수다. 따라서 처음 몇 순간은 다음과 같다.

${\displaystyle \mu _{1}={\sqrt{2}}\,\,{\frac {\감마(((k\!+\!1)/2)}{\감마(k/2)}}}$

${\displaystyle \mu _{2}=k\,}$

${\displaystyle \mu _{3}=2}{\sqrt{2}}\,\,{\frac {\감마(((k\!+\!3)/2)}{\감마(k/2)}}}}}}}{1}$

${\displaystyle \mu _{4}=(k)(k+2)\,}$

${\displaystyle \mu_{5}=4{\sqrt{2}}\,\,{\frac {\gamma(((k\!+\!5)/2)}{\Gamma(k/2)}}}}}}{1}$

${\displaystyle \mu _{6}=(k+2)(k+2)\,}$

감마함수에 대한 반복 관계를 사용하여 가장 오른쪽 식을 도출하는 경우:

${\displaystyle \감마(x+1)=x\감마(x)\,}$

이러한 표현에서 우리는 다음과 같은 관계를 도출할 수 있다.

평균: $\mu {\displaystyle }$= ${\displaystyle 2\sqrt{\mathrm{}}}$ ${\displaystyle \gamma \frac{\mathrm{}}{}}$(${\displaystyle \frac{}{}}$( ${\displaystyle \frac{k}{}}$+ ${\displaystyle \frac{1}{}}$)${\displaystyle \frac{}{}}$/ 2${\displaystyle \frac{}{}}$) ${\displaystyle \frac{\mathrm{}}{}}$( ${\displaystyle \frac{k\mathrm{}}{}}$/ ${\displaystyle \frac{2\mathrm{}}{}}$) ${\$$2$)$}{\감마(k/2}}:)},$라지 k의 $경우{\displaystyle \sqrt{}}$k - ${\displaystyle \sqrt{1\frac{\mathrm{}}{}}}$ ${\displaystyle \sqrt{\frac{2}{}}}${\$displaystyle${\$sqrt {k-{\tfrac{1$}{$2}}}$에 가깝다.

분산: ${\displaystyle V}$= ${\displaystyle k}$ -${\displaystyle {\mu \mathrm{}}^{}}$ 2 $displaystyle V=k-\mu ^{2$ k가 증가함에$$ 따라 ${\displaystyle \frac{1}{}}$ 2 ${\${\$tfrac{$1}{$2}}}$에 접근함

왜도: $\gamma {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle \mathrm{\mu }}$ ${\displaystyle \frac{{\sigma \mathrm{}}^{}}{}}$ 3${\displaystyle \frac{{}^{}}{}}$( 1${\displaystyle }$- ${\displaystyle 2}$ ${\displaystyle {\sigma \mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) ${\displaystyle \gamma _{1}={\frac }{\mu ^{3}}\,(1-2\sigma ^{2})}$

첨도 초과: ${\displaystyle {\gamma \mathrm{}}_{}}$ 2${\displaystyle {}_{}}$= ${\displaystyle 2\frac{\mathrm{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$( ${\displaystyle 1\mu }$ μ ${\displaystyle {\sigma \mathrm{}}_{}}$ 1${\displaystyle {}_{}}$- ${\displaystyle {\sigma \mathrm{}}^{}}$ 2${\displaystyle {}^{}}$) ${\displaystyle \gamma _{2}={\frac$ {$2}{\sigma ^{2}}(1-\mu \sigma \gma$ \{$1}-\sigma ^{2}}}}}$

엔트로피

엔트로피는 다음에 의해 주어진다.

${\displaystyle S=\ln(\감마(k/2))+{\frac {1}{1}:{2}}(k\!\\ln(2)\\(k\!\!1)\psi ^{0}(k/2)}$

여기서 ${\displaystyle \psi }$ ${\displaystyle {0\mathrm{}}^{}}$( z${\displaystyle }$) ${\displaystyle \property$^{$0}(z)}$은 다감마 함수다.

큰 n 근사치

우리는 기 분포의 평균과 분산의 큰 n=k+1 근사치를 발견했다. 여기에는 예를 들어, 정규 분포 모집단의 표본에 대한 표준 편차 분포를 찾는 데 적용되며, 여기서 n은 표본 크기입니다.

평균은 다음과 같다.

${\displaystyle \mu ={\sqrt {2}}:\,\,{\frac {\감마(n/2)}{\감마((n-1)/2)}}}$

Legendre 복제 수식을 사용하여 다음과 같이 기록하십시오.

${\displaystyle {2n}^{}}$- ${\displaystyle 2^{}}$ ${\displaystyle \mathrm{\gamma }}$(${\displaystyle }$( ${\displaystyle \mathrm{n}}$- ${\displaystyle 1}$)${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$) ${\displaystyle \cdot }$⋅ (${\displaystyle n}$/ ${\displaystyle 2\mathrm{}}$)${\displaystyle }$= ${\displaystyle \pi \sqrt{}}$ ${\displaystyle \gamma \mathrm{}}$ ${\displaystyle (n}$- ${\displaystyle 1}$) ${\displaystyle 2^{n-2}\\dcdot \Gamma (((n-1)/2)={\sqrt {\pi },$$,n-1$}

따라서:

${\displaystyle \mu ={\sqrt {2/\pi }\,2^{n-2}\,{\frac {(\감마(n/2)^{2}}}{\감마(n-1)}}$

감마 함수에 대한 스털링의 근사치를 사용하여 평균에 대한 다음 식을 얻는다.

${\displaystyle \mu ={\sqrt {2/\pi }}\,2^{n-2}\,{\frac {\left({\sqrt {2\pi }}(n/2-1)^{n/2-1+1/2}e^{-(n/2-1)}\cdot [1+{\frac {1}{12(n/2-1)}}+O({\frac {1}{n^{2}}})]\right)^{2}}{{\sqrt {2\pi }}(n-2)^{n-2+1/2}e^{-(n-2)}\cdot [1+{\frac {1}{12(n-2)}}+O({\frac {1}{n^{2}}})]}}}$

${\displaystyle =(n-2)^{1/2}\,\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]={\sqrt {n-1}}\,(1-{\frac {1}{n-1}})^{1/2}\cdot \left[1+{\frac {1}{4n}}+O({\frac {1}{n^{2}}})\right]}$

${\displaystyle ={\sqrt{n-1}\,\cdot \left[1-{\frac {1}{n^{2}}}\,\cdot \좌측[1+{4n}}{4n}}}}}+O({{n^{1}{n^2}}}}}}}}}})\오른쪽]$

${\displaystyle ={\sqrt{n-1}\,\cdot \left[1-{\frac {1}{4n}}}+O({\frac {1}{n^{2}}}\right]}}}}}}}$

따라서 분산은 다음과 같다.

${\displaystyle V=(n-1)-\mu ^{2}\,=(n-1)\cdot {\frac {1}{2n}\,\cdot \좌측[1+O({\frac {1}{n}}}})\오른쪽]}}$

관련 분포

• $X{\displaystyle }$ ~${\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$ X$\sim \chi _{k}}$일 경우 $X{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$~ ${\displaystyle {}_{}^{}}$ k ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$chi 제곱 분포)
• ${\displaystyle \underset{}{lim}}$ ${\displaystyle \underset{}{k}}$→${\displaystyle \frac{{}_{}{\mu k}_{}}{}}$ ${\displaystyle \frac{{\mu k}_{}}{}\stackrel{}{}}$→ ${\displaystyle d\stackrel{}{}}$ ${\displaystyle \stackrel{}{N}}$ ${\displaystyle (0,}$ ${\displaystyle 1}$) ${\$_${$d}\{xrigarrow{$d}\N$(0$,1)\,},}($정상 분포)
• ${\displaystyle X}$~ N${\displaystyle }$( ${\displaystyle 0}$, 1${\displaystyle }$) ${\$ X$\sim N (0,1)\,}$인 경우 ${\displaystyle X}$~ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ $displaystyle$ X $\sim \chi _{1}\,}$
• $X{\displaystyle }$~ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ $displaystyle X\sim \chi$ ${\displaystyle \_}$${1}\,}$인 경우 > ${\$$displaystyle$반정규 분포)은 ${\displaystyle \mathrm{for<img\; alt="\{\backslash displaystyle\; X\backslash sim\; \backslash chi\; \_\{1\}\backslash ,\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/6c2d76f086164fa94c4420cd0dc492e4a86b3a52"\; style="vertical-align:\; -0.671ex;\; width:7.975ex;\; height:2.509ex;"\; papago-attr-id="165">}}$ >${\displaystyle }$0 ${\displaystyle \{\backslash }$$displaystystyle \sigma >0\,},},}$
• ${\displaystyle {\chi }_{}}$ ${\displaystyle {2\mathrm{}}_{}}$~ ${\displaystyle \mathrm{R}}$ ${\displaystyle \mathrm{a}}$ l ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{i}}$ ${\displaystyle \mathrm{g}}$ ${\displaystyle \mathrm{h}}$( 1${\displaystyle }$) ${\$} (1$)\,}($레이리 분포)
• ${\displaystyle {\chi }_{}}$ ${\displaystyle {3\mathrm{}}_{}}$~ ${\displaystyle M\mathrm{}}$ ${\displaystyle \mathrm{a}}$ ${\displaystyle \mathrm{w}}$ ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{l}}$( ${\displaystyle 1}$) ${\$최대웰 분포)
• ${\displaystyle \ {\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\ _{2}\sim \chi _{k}}$, the Euclidean norm of a standard normal random vector of with ${\displaystyle k}$ dimensions, is distributed according to a chi distribution with ${\displaystyle k}$ degrees of freedom
• 기 분포는 일반화된 감마 분포 또는 나카가미 분포 또는 중심적이지 않은 기 분포의 특별한 경우다.
• 카이 분포의 평균($n{\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle n-1}$의 제곱근으로 스케일링$)$은 정규 분포의 표준 편차에 대한 불편 추정에서 보정 계수를 산출한다.

다양한 키 및 키 제곱 분포

이름	통계
카이 제곱 분포	${\displaystyle \sum _{i=1}^{k}\왼쪽({\frac {X_{i}-\mu_{i}}{i}}{\sigma _{i}}\오른쪽)^{2}}$
비중앙 카이-제곱 분포	${\displaystyle \sum _{i=1}^{k}\왼쪽({\frac {X_{i}}{\sigma _{i}}\오른쪽)^{2}}$
기 분포	${\displaystyle {\sqrt {\sum _{i=1}^{k}\왼쪽({\frac {X_{i}-\mu_{i}}}{\sigma _{i}}\오른쪽)^{2}}:$
비중앙 기 분포	${\displaystyle {\sqrt {\sum _{i=1}^{k}\좌측({\frac {X_{i}}{sigma _{i}}\오른쪽)^{2}}:$

참고 항목

• 나카가미 분포

참조

• Martha L. Abell, James P. Braselton, John Arthur Lafter, John A. 서까래, 수학 통계(1999년), 237f.
• Jan W. Goch, 폴리머 백과사전 제1권(2010), 부록 E, 페이지 972.

외부 링크

• http://mathworld.wolfram.com/ChiDistribution.html