파레토 분포

The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto,^[1] (Italian: [paˈreːto] US: /pəˈreɪtoʊ/ pə-RAY-toh),^[2] is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena. 원래 한 사회의 부의 분배를 설명하는 데 적용되었는데, 인구의 소수에 의해 부의 상당 부분이 점유되고 있는 추세에 적합하다.^[3][4] 결과의 80%가 파레토에 기인한다는 파레토 원칙이나 「80-20 규칙」은 파레토에 경의를 표하여 명명되었으나, 개념은 구별되며, 로그₄ 5 ≈ 1.16의 형상값(α)을 가진 파레토 분포만이 이를 정확하게 반영한다. 경험적 관찰 결과 이 80-20 분포는 자연현상이나^[5] 인간활동 등 광범위한 사례에 적합하다는 것을 알 수 있었다.^[6]

^[7]

정의들

X가 Pareto(타입 I) 분포를 갖는 랜덤 변수인 경우 X가 일부 숫자 x보다 클 확률, 즉 생존 함수(꼬리 함수라고도 함)가 다음과 같이 주어진다.^[8]

${\displaystyle {\overline {F}}(x)=\Pr(X>x)={\begin{cases}\left({\frac {x_{\mathrm {m} }}{x}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\1&x<x_{\mathrm {m} },\end{cases}}}$

여기서 x는_m (필요하게 양)의 최소 가능한 X 값이고, α는 양의 매개변수다. 파레토 1형 분포는 척도 모수 x와_m 형상 모수 α가 특징인데, 이를 꼬리 지수라고 한다. 이 분포가 부의 분포를 모형화하는 데 사용될 때, 매개변수 α를 파레토 지수라고 한다.

누적분포함수

정의에서 모수 α와 x를_m 갖는 파레토 랜덤 변수의 누적 분포 함수는

${\displaystyle F_{X}(x)={\begin{case}왼쪽({\frac {x_{\mathrm{m}}{x}}}\alpha }&x\geq x_{\mathrm {m}},\0&x_{mathrm}}}{case}}}}}}}}}}}$

확률밀도함수

확률밀도함수가 (분화에 의해) 다음과 같이 된다.

${\displaystyle f_{X}(x)={\begin{case}{\frac {\alpha x_{\mathrm {m}}}{x^{\x^{\alpha +1}}}{x\mathrm {m}},\0&x_{mathrm}{case}}}}}}}}}}$

선형 축에 표시되면 분포는 직교 축 각각에 점증적으로 접근하는 익숙한 J자형 곡선을 가정한다. 곡선의 모든 세그먼트는 자체 유사하다(적절한 스케일링 요인에 따라 달라짐). 로그 그림에 표시된 경우 분포는 직선으로 표시된다.

특성.

모멘트 및 특성 함수

• Pareto 분포에 따른 랜덤 변수의 기대값은 다음과 같다.

${\displaystyle \operatorname {E}(X)={\begin{case}\inflit &\alpha \leq 1,\\\\\\frac {\alpha x_{\mathrm{m}}}}{\alpha -1}&\alpha >1.\end{case}}}$

• 파레토 분포에 따른 랜덤 변수의 분산은

${\displaystyle \operatorname {Var}(X)={\begin{case}\input &\alpha \in]\\\\frac({\frac {x_{\mathrm{m}}{\alpha -1}}}\alpha -2}}\alpha >2).\end{case}}}$

(α α α 1이면 분산이 존재하지 않는다.)

• 그 순간은

${\displaystyle \mu_{n}={\n}={\n1}\frac \leqn,\\\\frac {\frac \\n_{\m}}^{\n}}}{\matrix -n}&###n.n.\end{case}}}$

• 모멘트 생성 함수는 다음과 같이 비양수 값 t ≤ 0에 대해서만 정의된다.

${\displaystyle M\left(t;\alpha ,x_{\mathrm {m}\오른쪽)=\E}\left[e^{tX}\right]=\alpha(-x_{m}t)^{\Alpha,-x_{mathrm}}t}}}}}$

${\displaystyle M\left(0,\alpha ,x_{\mathrm {}}\오른쪽)=1.}$

${\displaystyle \mathrm{따라서}}$ t${\displaystyle }$= 0 ${\displaystyle t=0}$을(를) 포함하는 열린 간격에 기대치가 수렴되지 않기 때문에 모멘트$$ 생성 기능이 존재하지 않는다고 본다.

• 특성 함수는 다음과 같다.

${\displaystyle \varphi(t;\alpha ,x_{\mathrm {m}}}=\알파(-ix_{\mathrm {m}}t)^{\알파(-\alpha,-ix_{\mathrm}t),}}}$

여기서 γ(a, x)은 불완전한 감마함수다.

매개변수는 모멘트 방법을 사용하여 해결할 수 있다.^[9]

조건부 분포

$x{\displaystyle {}_{}}$ m {\displaystyle$$$x_{\text{m}}$을 초과하는$$ 특정 숫자 ${\displaystyle {x\mathrm{}}_{}}1{\displaystyle {}_{}}$ {\$displaystyle$ $x_$${\$text{$m$$}$보다 크거나 같은 사건을 고려할 때 Pareto 분포의 조건부 확률 분포는 동일한$$ $Pareto{\displaystyle }$ 분포이지만$최소값$이다. ${\displaystyle {}_{}}$$x{\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\$ 대신$$$$x 1 ${\$1}. 이것은 conditional 예상 값(만약 유한, 즉 α 1{\displaystyle \alpha 1})x1{\displaystyle x_{1}에}비례합니다. 개체의 수명을 묘사하고 확률 변수의 경우, 이것은 그러한 기대 수명 시대로, 그리고 린디 효과 또는 린디의 법안은 정비례한다 의미를 암시한다.[10]

특성화 정리

$X{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ $3$${\displaystyle {}_{}}$,${\displaystyle }$… ${\displaystyle X_{1},X_{2},X_{3},\dotsc }}$은(는) 일부 m>에 대해$$$$[$x_{\$$text$${m},\$$inflt$ $)$ 간격으로 확률 분포를 지원하는 동일한 독립된 랜덤 변수라고 가정합시다$.$$}}>0}$. Suppose that for all ${\displaystyle n}$, the two random variables ${\displaystyle \min\{X_{1},\dotsc ,X_{n}\}}$ and ${\displaystyle (X_{1}+\dotsb +X_{n})/\min\{X_{1},\dotsc ,X_{n}\}}$ are independent. 그렇다면 공통분포는 파레토분포다.^{[citation needed]}

기하 평균

기하 평균(G)은^[11]

${\displaystyle G=x_{\text{m}\exp \left({\frac {1}{\alpha }}\오른쪽).}$

조화 평균

고조파 평균(H)은^[11]

${\displaystyle H=x_{\text{m}\왼쪽(1+{\frac {1}{\alpha }}\오른쪽).}$

그래픽 표현

선형 척도에 표시할 때 특성 곡선 '긴 꼬리' 분포는 로그 로그 그래프에 표시될 때 함수의 기본 단순성을 가린 다음 음의 구배를 갖는 직선의 형태를 취한다. 확률밀도함수에 대한 공식에서 x x_m x에 대해,

${\displaystyle \log f_{X}(x)=\log(\alpha {x_{\mathrm{m}}}}^{x^{\alpha +1}}}}}}}{x^{\alpha +1}\log(\alpha \log)\}$

α는 양성이므로 구배 -(α + 1)는 음이다.

관련 분포

일반화 파레토 분포

파레토 분포에는 파레토 유형 I, II, III, IV, 그리고 펠러-파레토 분포로 알려진 파레토 분포의 계층이 있다.^[8][12][13] 파레토 타입 4는 파레토 타입 I-를 포함한다.특별한 경우로서 III. 펠러-파레토^[12][14] 분포는 파레토 타입 4를 일반화한다.

파레토형 I-IV

파레토 분포 계층은 생존 함수(완전 CDF)를 비교하는 다음 표에 요약되어 있다.

μ = 0일 때 파레토 분포 타입 II는 로맥스 분포라고도 한다.^[15]

이 절에서는 x의 최소값을 나타내기 위해 이전에 사용된 기호 x를_m σ으로 대체한다.

형상 모수 α는 꼬리 지수, μ는 위치, μ는 척도, γ은 불평등 모수다. 파레토형(IV)의 특수한 경우는 다음과 같다.

${\displaystyle P(IV)(\sigma ,\sigma ,1,\alpha )=P(I)(\sigma ,\alpha )}$

${\displaystyle P(IV)(\mu ,\sigma ,1,\alpha )=P(II)(\mu ,\sigma ,\alpha )}$

$(\displaystyle P(IV)(\mu ,\sigma ,1)=P(III)(\mu ,\sigma ,\gamma).}$

평균의 미세성, 분산의 존재와 미세성은 꼬리 지수 α(부질 지수 α)에 따라 달라진다. 특히 부분 Δ-모멘트는 아래 표와 같이 일부 Δ > 0에 대해 유한하며, 여기서 Δ는 반드시 정수일 필요는 없다.

펠러-파레토 분포

Feller는^[12][14] 확률밀도함수가 다음과 같은 베타 랜덤 변수 Y의 변환⁻¹ U = Y - 1에 의해 파레토 변수를 정의한다.

${\displaystyle f(y)={\frac {y^{\gamma_{1}-1(y)^{{1}{1}-{2}-1}{{2}-1}{B(\gamma_{1},\gamma_{2}}}}}}},\qquad 0<1;1;감마_{2},},}$

여기서 B( )는 베타 함수다. 만약

${\displaystyle W=\mu +\sigma (Y^{-11)^{\gamma },\qquad \sigma >0,\gamma >0,}$

W는 Feller-Pareto 분포 FP(μ, σ, σ, γ₁, γ₂)를 갖는다.^[8]

If ${\displaystyle U_{1}\sim \Gamma (\delta _{1},1)}$ and ${\displaystyle U_{2}\sim \Gamma (\delta _{2},1)}$ are independent Gamma variables, another construction of a Feller–Pareto (FP) variable is^[16]

${\displaystyle W=\mu +\sigma \왼쪽({\frac {U_{1}:{1}{U_{2}}}\오른쪽)^{\gamma }}}}}}$

W ~ FP(μ, σ, Δ₁, Δ₂)라고 쓴다. 펠러-파레토 분포의 특별한 경우는 다음과 같다.

${\displaystyle FP(\sigma ,\sigma ,1,\alpha )=P(I)(\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,1,\alpha )=P(II)(\mu ,\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,1)=P(III)(\mu ,\sigma ,\gamma )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,\alpha )=P(IV)(\mu ,\sigma ,\gamma ,\alpha).}$

지수 분포와의 관계

파레토 분포는 다음과 같은 지수 분포와 관련이 있다. X가 최소 x와_m 지수 α로 파레토분산된 경우

${\displaystyle Y=\log \left({\frac {X}{x_{\mathrm {m}}}}\오른쪽)}$

속도 매개변수 α로 기하급수적으로 분포한다. 동등하게 Y가 비율 α로 기하급수적으로 분포하는 경우

${\displaystyle x_{\mathrm {}e^{Y}}$

파레토는 최소 x와_m 지수 α로 분배된다.

이는 표준 가변 변경 기법을 사용하여 확인할 수 있다.

${\displaystyle {\begin{aigned}\Pr(Y<Y>)&=\Pr \left(\log \left)({\frac {X}{x_{\m}}\right)\\\\&=\Pr(X<x_{\matrm {}e^{y}})=1-\좌({\frac {x_{\matrm {m}{}}}{x_{{m}}{e^}}}\right)^{\alpha }=1-e^{-\alpha y}.\end{정렬}}}$

마지막 식은 비율 α를 갖는 지수 분포의 누적 분포 함수다.

파레토 분포는 계층적 지수 분포로 구성할 수 있다.^[17] $\varphi {\displaystyle }$ ${\displaystyle a}$~ ${\displaystyle \mathrm{Exp}}$ (${\displaystyle }$) ${\displaystyle \pi a\sim {\text{$$Exp}(a)}$ 및$$ $\eta {\displaystyle }$ ${\displaystyle \eta }$~ ${\displaystyle \text{Exp}}$ (${\displaystyle \varphi }$ ) ${\displaystyle \eta \phi \sim {\text{$$Exp}(\phi$ $)\}.$ 그러면 ${\displaystyle p\frac{}{}}$(${\displaystyle \eta }$ ${\displaystyle a}$ )${\displaystyle }$= ${\displaystyle \frac{{a\mathrm{}}^{}}{}}$ (${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{\eta {}^{}}{}}$) 2 ${\$ p$(\eta$ a$)={\frac {a}{(a+\eta )^{2$}},$$$그$ 결과 +${\displaystyle \mathrm{\eta \eta }}$ ~${\displaystyle \text{파레토}(,}$ $){\displaystystyle$ a$+\esim{Pareto$$1}$가 있다$.$

일반적으로 $\lambda {\displaystyle }$~ ${\displaystyle \text{감마}(\alpha }$ ,${\displaystyle \beta }$) ${\displaystyle \lambda \sim{\text{Gamma}(\alpha ,\beta )}($shape-rate parametrization) 및 ${\displaystyle \eta }$~ ${\displaystyle \text{Exp}}$(${\displaystyle \lambda )}$ ${\displaystystyled \eta \lamda \sim {\\\ciptext}$$Exp}}(\lambda$ $)\},$ 그 다음 $\beta {\displaystyle }$+ ${\displaystyle \eta }$~ ${\displaystyle \text{파레토}(\beta }$ ,${\displaystyle \alpha }$) ${\displaystyle \beta +\eta \sim{\text{Pareto}}}(\beta ,\alpha$ $)\}.$

동등하게 $Y{\displaystyle }$~ ${\displaystyle \text{감마}(\mathrm{\alpha }}$, 1${\displaystyle }$) ${\displaystyle$ Y$\sim {\text{Gamma}(\alpha ,$1$)$및$$ $X{\displaystyle }$~ ${\displaystyle \text{Exp}(1}$) ${\displaystyle$ X$\sim {\text${\text$}$$Exp1$ 그 다음 $x{\displaystyle {}_{}}$ ${\displaystyle m_{}({}_{}1\mathrm{}}$+ ${\displaystyle \frac{X}{}}$ ${\displaystyle Y}$) ~${\displaystyle \text{파레토}({}_{}}$ ${\displaystyle m_{}}$, $){\displaystyle x_{\text{m}\!$$\left(1+{\frac {X}{$$Y}\오른쪽)\심각{\text{Pareto}}(x_{\text{m},\alpha$ $)\}.$

로그 정규 분포와의 관계

파레토 분포와 로그 정규 분포는 동일한 유형의 수량을 설명하기 위한 대체 분포다. 둘 사이의 연결점 중 하나는 둘 다 지수 분포와 정규 분포 각각 다른 공통 분포에 따라 분포된 랜덤 변수의 지수 분포라는 점이다. (이전 섹션 참조)

일반화된 파레토 분포와의 관계

파레토 분포는 일반화된 파레토 분포의 특수한 경우로서, 유사한 형태의 분포의 계열이지만, 분포의 지지도가 로맥스 분포와 함께 (변수 지점에서) 아래쪽으로 경계를 이루거나 (둘 다 가변 지점에서) 위아래로 경계를 이루거나 둘 다(둘 다 가변적인 경우)로 경계를 이루도록 추가 매개변수를 포함하고 있다.특례로 또한 이 패밀리는 부동 지수 분포와 시프트 지수 분포를 모두 포함한다.

The Pareto distribution with scale ${\displaystyle x_{m}}$ and shape ${\displaystyle \alpha }$ is equivalent to the generalized Pareto distribution with location ${\displaystyle \mu =x_{m}}$, scale ${\displaystyle \sigma =x_{m}/\alpha }$ and shape ${\displaystyle \xi =$$1/\alpha$ $\}.$ 반대로, 파레토 분포를 GPD에서 x ${\displaystyle m_{}}$= ${\displaystyle \sigma }$/ ${\displaystyle \xi }$ / ξ$$ξ { { ${$ { { { { { { { ${${ { \$sigma /\xi$ ${\displaystyle \},}$ α$$ = 1 /${\displaystyle \xi }$ \$\displaysty$ \$alpha =1/\xi$

바운드 파레토 분포

경계(또는 잘린) 파레토 분포에는 세 가지 모수가 있다: α, L, H. 표준 파레토 분포 α와 같이 형상을 결정한다. L은 최소값을 나타내며, H는 최대값을 나타낸다.

확률밀도함수는

${\displaystyle \frac{\alpha }{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{}^{}{}^{}}{}}$ x -${\displaystyle \frac{{}^{}}{\mathrm{}}}$- ${\displaystyle \frac{1^{}}{}}$- (${\displaystyle \frac{{}^{}}{}}$(${\displaystyle \frac{{\frac{L}{}}^{}}{}}$H ) ${\displaystyle \frac{{}^{}}{}}${\frac $스타일 {\frac{\fraca$ L$^{\x^{-\alpha -1}{1-\1}{\frac{L}}\right)^{\frac${{H}}}}}}}}}}:{\alpha$\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\}\},,$

여기서 L ≤ x ≤ H 및 α > 0.

경계 Pareto 랜덤 변수 생성

U가 (0, 1)에 균일하게 분포되어 있으면 역변환법을 적용한다.

${\displaystyle U={\frac {1-L^{\alpha }x^{-\alpha }}{1-({\frac{L}{H}}})^{\alpha }}}}}}}}}}}}}}$

${\displaystyle x=\lp(-{\frac {UH^{\alpha }-UL^{}-L^{\alpha }}}{H^{\L^{\alpha }}}\오른쪽)^{-{\frac {1}{\alpha }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

파레토에 분산된 경계선이야

대칭 파레토 분포

Symmetric Pareto 분포와 Zero Symmetric Pareto 분포의 목적은 날카로운 확률 피크와 대칭 긴 확률 꼬리로 이루어진 일부 특수 통계 분포를 포착하는 것이다. 이 두 분포는 파레토 분포에서 파생된 것이다. 일반적으로 긴 확률 꼬리는 확률이 천천히 감소한다는 것을 의미한다. 파레토 분포는 많은 경우에 피팅 작업을 수행한다. 그러나 분포가 대칭 구조로 되어 있고 두 개의 천천히 썩어가는 꼬리가 있다면 파레토는 그것을 할 수 없었다. 대신 Symmetric Pareto 또는 Zero Symmetric Pareto 분포를 적용한다.^[19]

대칭 파레토 분포의 누적분포함수(CDF)는 다음과 같이 정의된다.^[19]

${\displaystyle F(X)=P(x<X)={\begin{cases}{\tfrac {1}{2}}({b \over 2b-X})^{a}&X<b\\1-{\tfrac {1}{2}}({\tfrac {b}{X}})^{a}&X\geq b\end{cases}}}$

해당 확률밀도함수(PDF)는 다음과 같다.^[19]

${\displaystyle p(x)={ab^{a} \over 2(b+\왼쪽\vert x-b\right\vert )^{a+1},X\in R}$

이 분포에는 a와 b라는 두 개의 모수가 있다. 그것은 b에 의해 대칭이다. 그러면 수학적인 기대는 b이다. 다음과 같은 분산을 갖는 경우:

${\displaystyle E((x-b)^{2}=\int_{-\infit }^{{-\infit }^{2}p(x)dx={2b^{2} \over (a-1)}}}$

ZSP(Zero Symmetric Pareto) 분포의 CDF는 다음과 같이 정의된다.

${\displaystyle F(X)=P(x)={\begin{case}{\tfrac {1}{1}{b \b-X}^{a}&X<0\\\\\1-{\tfrac {1}{b}{b+X}}})^{a}&X\geq 0\end{case}}$

해당 PDF:

${\displaystyle p(x)={ab^{a} \over 2(b+\왼쪽\vert x\right\vert )^{a+1},X\in R}$

이 분포는 0으로 대칭이다. 매개변수 a는 확률의 붕괴율과 관련되며 (a/2b)는 확률의 피크 크기를 나타낸다.^[19]

다변량 파레토 분포

일변량 파레토 분포는 다변량 파레토 분포로 확장되었다.^[20]

통계적 추론

모수 추정

독립 표본 x = (x₁, x₂, x, ..., x_n)가 주어진 파레토 분포 모수 α와 x에_m 대한 우도 함수는

${\displaystyle L(\alpha ,x_{\mathrm {m} })=\prod _{i=1}^{n}\alpha {\frac {x_{\mathrm {m} }^{\alpha }}{x_{i}^{\alpha +1}}}=\alpha ^{n}x_{\mathrm {m} }^{n\alpha }\prod _{i=1}^{n}{\frac {1}{x_{i}^{\alpha +1}}}.}$

따라서 로그우도함수는

${\displaystyle \ell(\property,x_{\mathrm {m})=n\ln \n\n\n\n\matrm {m}-(\m}-)(\matrix +1)\sum _{i=1^{n}\ln x_{i}.}$

$\ell {\displaystyle }$(${\displaystyle \alpha }$, ${\displaystyle {}_{}}$ ${\displaystyle m_{}}$) ${\displaystyle \ell(\alpha ,x_{\mathrm {m}}})$이_m x, 즉 x 값이_m 클수록 우도함수의 값이 단조롭게 증가하고 있음을$$ 알 수 있다. 따라서 x ≥ x 이후로는_m 다음과 같이 결론짓는다.

${\displaystyle {\widehat{x}_{\mathrm {m} }=\min _{i}{x_{i}}}.}$

α에 대한 추정기를 찾기 위해 해당 부분파생물을 계산하여 0인 위치를 결정한다.

${\displaystyle {\frac{\frac {\reason \l}}}={\frac {n}{\n}}{\m}-\sum _{i=1}{i=1}\ln x_{i}=0.}$

따라서 α에 대한 최대우도 추정기는 다음과 같다.

${\displaystyle {\widehat{\widehat{\n1}={\frac {n}{\sum _{i_{i}/{\widehat{x}_{\mathrm {m}}}}}}}.}$

예상되는 통계 오류:^[21]

${\displaystyle \chma ={\frac {\widehat {\reason}}{\sqrt{n}}.}$

말릭(1970년)[22]. 특히, x^ m{\displaystyle{\hat{)}}_{\mathrm{m}}}과α ^{\displaystyle{\hat{\alpha}}}과 x의 독립 ^ m{()^ m,α ^){\displaystyle({\hat{x}}_{\mathrm{m}},{\hat{\alpha}})}의 정확한 결합 분포 \display을 준다.styl$e {\hat{x}_{\mathrm{m}}}}}}$은(는) 스케일 파라미터 x와_m 형상 파라미터 nα를 가진 파레토(Pareto)인$$ 반면, $\alpha {\displaystyle \hat{}}$ ${\$은(는) 형상 및 스케일 파라미터 n - 1과 함께 역감마 분포를 가진다.

신뢰구간

Treating ${\displaystyle {\hat {\alpha }}}$ as known (i.e. ${\displaystyle \alpha ={\hat {\alpha }}}$) and using the result above by Malik (1970), the CDF of a Pareto(${\displaystyle x_{m}}$, ${\displaystyle n{\hat {\alpha }}}$) distribution can be inverted to form a confidence interval for ${\displaystyle x_{m}}$, i.e. CDF(${\displaystyle {\hat {x}}_{m}}$) = ${\displaystyle 1-{\Bigl (}{\frac {x_{m}}{{\hat {x}}_{m}}}{\Bigr )}^{n{\hat {\alpha }}}}$. Additionally, ${\displaystyle \alpha }$ could be profiled. 즉, 각 가설 $H{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$: ${\displaystyle {}_{}}$ ${\displaystyle m_{}}$ ${\displaystyle {}_{}}$ x ${\displaystyle {m{}_{}}_{}}$ 0 ${\$ $\alpha {\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\$을(를) 생성하는 제한된 귀무 공간 아래에서$$ $\alpha {\displaystyle }$ ${\\\\$d}을 다시 $추정하여$알려진 것으로$$간주한다$$$$. 단측 97.5% 신뢰 하한은 $x{\displaystyle {\stackrel{}{}}_{}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle m_{}}$ ${\$ 또는 그보다$$ 극단적인 것의 위쪽 꼬리 확률이 2.5%인 x $m{\displaystyle {}_{}}$ ${\$에 대한 가설이다. A similar approach can be used to obtain a confidence interval for ${\displaystyle \alpha }$ by inverting the CDF of an inverse-gamma distribution with shape and scale parameters ${\displaystyle n-1}$ and ${\displaystyle n\alpha }$, respectively, i.e. CDF(${\displaystyle {\hat {\alpha }}}$) = ${\displaystyle \frac{\mathrm{\Gamma }}{}}$${\displaystyle {\frac {\Gamma {\Bigl (}n-1,{\frac {n\alpha }{\hat {\alpha }}}{\Bigr )}}{\Gamma (n-1)}}}$. The two-sided 95% confidence limits are the hypotheses for ${\displaystyle \alpha }$ such that the one-sided probability of ${\displaystyle {\hat {\alpha }}}$ or 좀 더 극단적인 것은 2.5%이다.

발생 및 적용

일반

Vilfredo Pareto는 원래 이 분포를 개인들 간의 부의 배분을 묘사하기 위해 사용했다. 왜냐하면 그것은 사회의 부의 많은 부분이 그 사회의 더 작은 비율의 사람들에 의해 소유된다는 것을 오히려 잘 보여주는 것처럼 보였기 때문이다. 그는 또한 소득의 분배를 묘사하는 데 그것을 이용했다.^[4] 이런 생각은 파레토 원칙이나 인구의 20%가 부의 80%를 지배한다는 '80-20 규칙'으로 더 단순하게 표현되기도 한다.^[23] 그러나 80-20규칙은 α의 특정 값에 해당하며, 사실 파레토가 쿠르스 데코노미 정치에서 영국 소득세에 관한 자료를 보면 인구의 약 30%가 약 70%의 소득을 가지고 있음을 알 수 있다.^{[citation needed]} 이 글의 앞부분의 확률밀도함수(PDF) 그래프를 보면 1인당 소량의 부를 소유한 인구의 "확률"이나 분수가 다소 높다가 재산이 증가함에 따라 꾸준히 감소한다는 것을 알 수 있다. (그러나 파레토 분포는 하층부의 재물에 대해서는 현실적이지 않다. 사실 순자산은 마이너스일 수도 있다.) 이러한 분포는 부나 소득을 기술하는 데 국한되지 않고, '소형'에서 '대형'으로의 분포에서 평형이 발견되는 많은 상황에 한정된다. 다음과 같은 예들이 때때로 대략적으로 파레토 유통으로 보여진다.

• 인간 거주지의 크기(많은 도시, 많은 햄릿/마을)^[24][25]
• TCP 프로토콜을 사용하는 인터넷 트래픽의 파일 크기 분포(많은 작은 파일, 적은 수의 큰 파일)^[24]
• 하드 디스크 드라이브 오류율^[26]
• 보세-아인슈타인의 절대 영도^[27] 부근 응축수의 군집

• 유전에서의 석유 매장량 값(큰 밭 몇 개, 작은 밭 여러 개)^[24]
• 슈퍼컴퓨터에 할당된 작업의 길이 분포(대형 몇 개, 소형 여러 개)^[28]
• 개별 주식의 표준화된 주가수익률
• 모래 입자의 크기
• 운석의 크기
• 일반 책임, 상용 자동차 및 근로자 보상과 같은 특정 사업군에 대한 대규모 사상자 손실의 심각성.^[29][30]
• 스팀에서 사용자가 다른 게임을 하는 데 소비하는 시간. (일부 게임은 많이 하지만 대부분은 거의 하지 않는다.) [2]^{[original research?]}
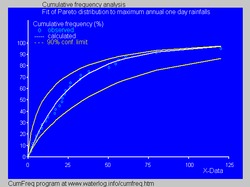
• 수문학에서 파레토 분포는 연간 최대 1일 강우량 및 하천 방류와 같은 극단적인 사건에 적용된다.^[31] 파란색 그림은 파레토 분포를 연간 최대 1일 강우량에 맞추는 예를 보여 주며, 이항 분포를 기준으로 90% 신뢰 벨트를 보여준다. 강우 데이터는 누적 빈도 분석의 일부로 위치를 표시하여 나타낸다.
• 전기 유틸리티 분배 신뢰성(고객 회의록의 80%가 해당 연도의 약 20%에 해당)

Zipf의 법칙과의 관계

파레토 분포는 연속 확률 분포다. 때때로 제타 분포라고도 불리는 Zipf의 법칙은 이산형 분포로, 값을 단순한 순위로 구분한다. 둘 다 음의 지수를 갖는 단순한 전력법칙으로, 누적 분포가 1. $X{\displaystyle }$ ${\displaystyle x}$ 값(수치)을$$ $N{\displaystyle }$ ${\displaystyle N}$ 등급으로$$ 고정하여 각 빈에 있는 사람 수가 1/순위 패턴을 따르도록 한다면 Zipf는 파레토 분포에서 파생될 수 있다. The distribution is normalized by defining ${\displaystyle x_{m}}$ so that ${\displaystyle \alpha x_{\mathrm {m} }^{\alpha }={\frac {1}{H(N,\alpha -1)}}}$ where ${\displaystyle H(N,\alpha -1)}$ is the generalized harmonic number. 이것은 Zipf의 확률밀도함수를 파레토에서 도출할 수 있게 한다.

${\displaystyle f(x)={\frac {\alpha x_{\mathrm {m}}^{}{x^{\alpha +1}={\frac {1}{x^{s}H(N,s)}}}}}}}}}}$

여기서 s${\displaystyle }$= ${\displaystyle \alpha }$- ${\displaystyle 1}$ ${\displaystyle s=\alpha -1}$ 및$$ $x{\displaystyle }$ ${\displaystyle x}$은 1부터 N까지의 순위를 나타내는 정수이며$$, N은 가장 높은 소득 계층이다. 따라서 모집단(또는 언어, 인터넷 또는 국가)에서 무작위로 선택한 사람(${\displaystyle \mathrm{또는}}$ 단어, 웹사이트 링크 또는 도시)은 $f{\displaystyle }$( x${\displaystyle }$) ${\displaystyle f(x)}$의 순위 $x{\displaystyle }$ ${\displaystyle x}$ 확률을$$ 가진다$.$

"파레토 원칙"과의 관계

The "80–20 law", according to which 20% of all people receive 80% of all income, and 20% of the most affluent 20% receive 80% of that 80%, and so on, holds precisely when the Pareto index is ${\displaystyle \alpha =\log _{4}5={\cfrac {\log _{10}5}{\log _{10}4}}\app$$rox$ 1$.152$}$$. 이 결과는 아래에 주어진 로렌츠 곡선 공식에서 도출할 수 있다. 더욱이 다음은 수학적으로 동등한 것으로 나타났다^[32].

• 소득은 파레토 분포에 따라 지수 α > 1로 분배된다.
• 전체 인구의 100p %가 전체 소득의 100(1 - p)%를 받고, 마찬가지로 모든 실질(정수 아님) n > 0에서 100pⁿ %가 전체 소득의 100(1 - p)ⁿ 퍼센트를 받는 숫자 0이 있다. α와 p는 다음과 같다.

${\displaystyle 1-{\frac {1}{\p}}={\frac {\ln(p)}{\ln(p)}}{\ln(p^{n}}}}}}}}$

이는 소득에만 적용되는 것이 아니라 재산에도, 또는 이 분배에 의해 모델링될 수 있는 그 밖의 어떤 것에도 적용된다.

여기에는 위에서 언급한 바와 같이 0 < α α α 1이 무한 기대치를 가지므로 소득분배를 합리적으로 모형화할 수 없는 파레토 분배가 제외된다.

프라이스의 법칙과의 관계

프라이스의 제곱근법은 파레토 분포의 재산 또는 이와 유사한 재산으로 제공되기도 한다. 그러나 법은 $\alpha {\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \alpha =1}$인 경우에만 적용된다$.$ 이 경우 총 재산과 기대 재산액이 정의되지 않으며 규칙은 무작위 표본에만 점증적으로 적용된다는 점에 유의한다. 위에서 언급한 파레토 확대 원칙은 훨씬 더 일반적인 규칙이다.

로렌츠 곡선 및 지니 계수

로렌츠 곡선은 종종 소득과 부의 분배를 특징짓는 데 사용된다. 모든 분포의 경우 로렌츠 곡선 L(F)은 PDF f 또는 CDF F의 관점에서 다음과 같이 기록된다.

${\displaystyle L(F)={\frac {\int _{x_{\mathrm {m} }}^{x(F)}xf(x)\,dx}{\int _{x_{\mathrm {m} }}^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}}$

여기서 x(F)는 CDF의 역이다. 파레토 분포를 위해서

${\displaystyle x(F)={\frac {x_{\mathrm {m}}}}^{\frac {1}{\alpha }}}}}$

로렌츠 곡선은

${\displaystyle L(F)=1-(1-F)^{1-{\frac {1}{\alpha }}}$

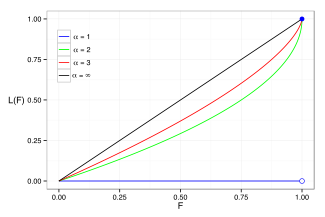
< α ${\displaystyle 0<\alpha \leq 1}$의 경우 분모는 무한하며 L=0을 산출한다. 다수의 파레토 분포에 대한 로렌츠 곡선의 예는 오른쪽 그래프에 나와 있다.

옥스팜(2016년)에 따르면 세계에서 가장 부유한 62명은 세계 인구의 가장 가난한 절반에 버금가는 부를 갖고 있다.^[33] 우리는 이 상황에 적용될 파레토 지수를 추정할 수 있다. ▼를 ${\displaystyle 62}$/${\displaystyle }$( ${\displaystyle 7}$ ${\displaystyle \times }$ ${\displaystyle {10}^{}}$ ${\displaystyle {9\mathrm{}}^{}}$) ${\displaystyle 62/(7\time 10^{9})$로 지정:

${\displaystyle L(1/2)=1-L(1-\varepsilon )}$

또는

${\displaystyle 1-(1/2)^{1-{\frac {1}{\frac }}}=\varepsilon ^{1-{\frac {1}{\frac }}}}}}}}}}}$

해결책은 α가 약 1.15와 같으며, 재산의 약 9%는 두 집단이 각각 소유하고 있다는 것이다. 그러나 실제로 세계 성인 인구의 69%가 재산의 약 3%만을 소유하고 있다.^[34]

지니계수는 [0, 0]과 [1, 1]을 연결하는 선인 등분포선에서 로렌츠 곡선의 편차를 측정한 것으로, 오른쪽 로렌츠 플롯에서 검은색(α = α)으로 표시된다. 구체적으로 지니계수는 로렌츠 곡선과 등분포선 사이의 면적의 두 배다. 그런 다음 파레토 분포에 대한 지니계수를 계산한다($\alpha {\displaystyle }$ ${\displaystyle \ge }$ ${\displaystyle 1}$ ${\displaystyle \alpha \geq$ 1$\}).$

${\displaystyle G=1-2\left(\int_{0}^{1}L(F)\,dF\right)={\frac {1}{2\alpha -1}}}$

(Aabberge 2005 참조).

계산 방법

랜덤 표본 생성

랜덤 표본은 역변환 샘플링을 사용하여 생성할 수 있다. 단위 간격(0, 1)의 균등 분포에서 무작위 변수 U를 구하면 다음과 같이 T를 구한다.

${\displaystyle T={\frac {x_{\mathrm {m}}}}{U^{1/\alpha }}}}}}}$

파레토 ^[35]배급이야 [0, 1]에 U를 균일하게 배분하면 (1 - U)와 교환할 수 있다.

참고 항목

• 브래드포드의 법칙
• 구텐베르크-리히터 법칙
• 매슈 효과
• 파레토 분석
• 파레토 효율
• 파레토 보간법
• 전력법 확률 분포
• 스터전의 법칙
• 트래픽 생성 모델
• 지프의 법칙
• 굵은꼬리분포

참조

메모들

• M. O. Lorenz (1905). "Methods of measuring the concentration of wealth". Publications of the American Statistical Association. 9 (70): 209–19. Bibcode:1905PAmSA...9..209L. doi:10.2307/2276207. JSTOR 2276207.
• Pareto, Vilfredo (1965). Librairie Droz (ed.). Ecrits sur la courbe de la répartition de la richesse. Œuvres complètes : T. III. p. 48. ISBN 9782600040211.

• Pareto, Vilfredo (1895). "La legge della domanda". Giornale Degli Economisti. 10: 59–68.
• Pareto, Vilfredo (1896). "Cours d'économie politique". doi:10.1177/000271629700900314. S2CID 143528002. Cite 저널은 필요로 한다. journal= (도움말)

외부 링크

• "Pareto distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Pareto distribution". MathWorld.
• Aabergé, Rolf (May 2005). "Gini's Nuclear Family". International Conference to Honor Two Eminent Social Scientists (PDF).

• Crovella, Mark E.; Bestavros, Azer (December 1997). Self-Similarity in World Wide Web Traffic: Evidence and Possible Causes (PDF). IEEE/ACM Transactions on Networking. 5. pp. 835–846. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-02-25.

• syntraf1.c는 경계 Pareto 버스트 크기와 지수 인터버스트 시간으로 합성 패킷 트래픽을 생성하기 위한 C 프로그램이다.