타르스키의 공리

타르스키의 공리는, 알프레드 타르스키 때문에, 정체성을 가진 1차 논리학에서 공식화할 수 있는 유클리드 기하학의 실질적인 파편을 위해 설정된 공리로, 정해진 이론이 필요 없는 (타르스키 1959) (즉, 기본 이론으로서 공식화될 수 있는 유클리드 기하학의 그 부분)이다. 유클리드 기하학의 다른 현대적 공리는 힐베르트의 공리와 비르코프의 공리다.

개요

그의 경력 초기에 타르스키는 기하학을 가르치고 세트 이론을 연구했다. 그의 동료 스티븐 기반트(1999)는 타르스키의 도약 지점을 이렇게 설명했다.

타르스키는 엔리케스로부터 페아노의 영향을 강하게 받은 이탈리아의 지오미터 마리오 피에리의 작품을 알게 되었다. 타르스키는 논리적 구조와 공리의 복잡성이 더욱 투명하게 드러나는 피에리의 [그의 포인트와 스피어 회고록] 시스템을 선호했다.

그러자 기반트는 "전형적인 철저함으로" 타르스키가 자신의 시스템을 고안했다고 말한다.

타르스키의 기하학적 접근방식은 어떤 점이 달랐는가? 우선, 공리계는 그 때까지 존재했던 어떤 공리계보다 훨씬 단순했다. 사실 타르스키의 모든 공리의 길이는 피에리의 24개 공리의 하나 이상에 지나지 않는다. 모든 공리가 정해진 관념의 도움 없이 원시적인 관념으로만 표현될 수 있을 만큼 간단한 유클리드 기하학의 첫 번째 체계였다. 훨씬 더 중요한 것은, 처음으로 완전한 기하학과 그것의 기초, 즉 그것의 첫 번째 순서가 명확한 구별이 이루어졌다.

타르스키스는 유클리드 기하학의 다른 현대적 공리화처럼 문장이라고 불리는 기호 문자열로 구성된 형식 체계를 채용하는데, 그 구조는 형식적인 구문론적 규칙과 문장의 허용된 조작을 결정하는 증명 규칙들을 존중한다. 타르스키의 공리화에는 비르코프나 힐베르트의 공리화와 같은 다른 현대의 공리화와는 달리 점 이외의 원시적인 물체가 없기 때문에 변수나 상수는 선이나 각도를 나타낼 수 없다. 점만이 유일한 원시적인 사물이고, 타르스키의 체계가 일차적인 이론이기 때문에 선을 점 집합으로 규정하는 것조차 불가능하기 때문이다. 유일한 원시적 관계(predictures)는 점들 사이의 "간격"과 "간격"이다.

타르스키의 공리화는 타르스키와 기반트(1999)가 명시적으로 말하는 의미에서 경쟁자보다 짧다. 피에리보다 더 간결한 것은 타르스키가 점, 중간, 일치의 세 가지를 소개한 반면 피에리는 원시적인 관념이 두 가지밖에 없었기 때문이다. 그러한 원시적이고 정의된 관념의 경제는 타르스키의 시스템이 유클리드 기하학을 하기에 그리 편리하지 않다는 것을 의미한다. 오히려 타르스키는 그의 시스템을 수학적 논리학의 도구, 즉 그 변태적 성질을 도출하는 것을 용이하게 하기 위해서 분석을 용이하게 하도록 설계했다. 타르스키의 체계는 모든 문장이 보편적으로 존재하는 형태로 쓰여질 수 있다는 특이한 속성을 가지고 있는데, 이는 혼전 정상 형태의 특수한 경우다. 이 형식은 존재론적 정량자 앞에 모든 보편적 정량자를 가지고 있어서 모든 문장은 sentences $\forall u\forall v\ldots \exists a\exists b\dots .$ $\forall u\forall v\ldots \exists a\exists b\dots .$ v … $\forall u\forall v\ldots \exists a\exists b\dots .$ a ∃ b … $\forall u\forall v\ldots \exists a\exists b\dots .$ . $\forall u\forall v\ldots \exists a\exists b\dots .$ {\ $displaystyle$ \ forall $u\dots \exist$ a\ $exists$ b\ $dots.}$ 이 $\forall u\forall v\ldots \exists a\exists b\dots .$ 사실은 타르스키가 유클리드 기하학이 디케이블이라는 것을 증명할 수 있게 했다: 진리를 결정할 수 있는 알고리즘이 존재한다.또는 어떤 문장의 허구. 타르스키의 공리화 역시 완결이다. 타르스키의 이론에는 로빈슨 산수를 해석하는 데 필요한 표현력이 결여되어 있기 때문에 이는 괴델의 첫 불완전성 정리(Franzén 2005, 페이지 25–26)와 모순되지 않는다.

공리

알프레드 타르스키(1959)는 1926년부터 1983년 사망할 때까지 간헐적으로 유클리드 기하학의 공리화와 변성술을 연구했으며, 타르스키(1959)는 이 주제에 대한 성숙한 관심을 예고했다. 유클리드 기하학에 관한 타르스키와 그의 제자들의 연구는 아래에 제시된 10개의 공리와 하나의 공리 스키마, 관련 변성법, 그리고 그 과목의 공정한 부분을 정리한 단문자 슈와바호이저, 스즈미에루, 타르스키(1983)에서 절정에 달했다. 굽타(1965)는 중요한 공헌을 했고, 타르스키와 기반트(1999)는 역사를 논한다.

근본관계

이 공리들은 유클리드 평면 기하학의 변성적 특성에 대한 조사의 일환으로 1920년대에 고안된 타르스키 세트의 보다 우아한 버전이다. 이 목표는 1차 이론으로 그 기하학을 재구성할 필요가 있었다. 타르스키는 점의 우주를 표방하며, 소문자는 그 우주를 가로지르는 변수를 나타낸다. 평등은 기본 논리에 의해 제공된다(제1차 논리#평등과 그 공리 참조).^[1] 타르스키는 그 후 두 가지 원시적인 관계를 맺었다.

삼위일체, 삼위일체. 원자문장 Bxyz 또는 (y)B(x,z)는 y가 "x와 z 사이"라는 것을 의미하며, 다시 말해서 y는 선분절 xz에 있는 점이라는 것을 의미한다.(이 관계는 포괄적으로 해석되므로 bxyz는 x=y 또는 y=z가 될 때마다 사소한 진실이다.
일치성(또는 "등가 저항성"), 4차 관계. 원자 문장 Cwxyz 또는 (w,x)C(y,z) 또는 일반적으로 wx x yz는 wx가 yz에 합치되는 것으로 해석될 수 있으며, 다시 말해 선 세그먼트 wx의 길이가 선 세그먼트 yz의 길이와 같다는 것이다.

간극은 유클리드 기하학의 친근한 측면(선들의 평행성 등), 일치성, 그 메트릭 측면(각도와 거리 등)을 포착한다. 배경 논리에는 정체성, 이항 관계가 포함된다. 공리는 다섯 차례에 걸쳐 정체성(또는 그 부정)을 불러온다.

아래의 공리는 그들이 호출한 관계의 종류에 따라 분류되고, 먼저 실존적 정량자의 수, 그 다음 원자 문장의 수로 분류된다. 공리는 보편적 폐쇄로 읽어야 한다. 따라서 자유 변수는 암묵적으로 보편적으로 수량화되어야 한다.

일치 공리

컨그루언스의 반사율: $xyex\equiv yx\,}$

컨그루언스의 정체성: $오른쪽 화살표는 x=y=y.}$

협곡의 변천성: $(xy\equiv zu\land xy\equiv vw)\오른쪽 화살표 zu\equiv vw.}$

해설

조합관계 $xy\equiv zw$ $xy\equiv zw$ $xy\equiv zw$ $xy\equiv zw$ $xy\equiv zw$ $xy\equiv zw$ 은 $xy\equiv zw$ (는) 점 사이의 4방향 관계인 반면, 비공식적으로 두 선 세그먼트 $x$ y $xy$ 와 $z$ $zw$ $zw$ 사이의 2진 관계라고도 생각할 수 있다 $zw$ 위의 "유연성"과 "투명성" 공리가 결합되어 다음 두 가지를 모두 증명한다.

이 이항 관계가 사실 동등성 관계라는 것
- 그것은 반사적이다: $xy\equiv xy$ $xy\equiv xy$ $xy\equiv xy$ $xy\equiv xy$ $xy\equiv xy$ $xy\equiv xy$ .
- 대칭 $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ z $xy\equiv zw\rightarrow zw\equiv xy$ → $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ $xy\equiv zw\rightarrow zw\equiv xy$ 입니다 $xy\equiv zw\rightarrow zw\equiv xy$
- transitive $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ z $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ u u $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ w ) $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ → $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$ w ${\displaystyle (xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv$ vw $(xy\equiv zu\land zu\equiv vw)\rightarrow xy\equiv vw$
선 세그먼트의 점이 지정되는 순서는 관련이 없다.
- $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ → $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ $xy\equiv zw\rightarrow xy\equiv wz$ ${\displaystyle xy\equiv zw\rightarrow xy\equiv wz$ .
- $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ → $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ $xy\equiv zw\rightarrow yx\equiv zw$ w $xy\equiv zw\rightarrow yx\equiv zw$ .
- $xy\equiv zw\rightarrow yx\equiv wz$ $xy\equiv zw\rightarrow yx\equiv wz$ $xy\equiv zw\rightarrow yx\equiv wz$ z $xy\equiv zw\rightarrow yx\equiv wz$ → $xy\equiv zw\rightarrow yx\equiv wz$ $xy\equiv zw\rightarrow yx\equiv wz$ $xy\equiv zw\rightarrow yx\equiv wz$ $xy\equiv zw\rightarrow yx\equiv wz$ z $xy\equiv zw\rightarrow yx\equiv wz$ .

'투명성' 공리는 유클리드(유클리드)의 '공통 관념' 중 첫 번째를 존중한다는 점에서 합성이 유클리드(유클리드)라고 단언한다.

"Congruence의 Identity of Congruence" 공리는 xy가 동일한 지점에서 시작하고 끝나는 세그먼트와 일치한다면 x와 y가 동일한 지점이라고 직관적으로 기술한다. 이것은 이항 관계에 대한 반사성 개념과 밀접한 관련이 있다.

중간도 공리

파슈의 공리

중간의 정체성: $bxyx\오른쪽 화살표 x=y.}$

선 세그먼트 $x$ $x$ $xx$ 의 유일한 $x$ 은 x $xx$ 그 자체뿐입니다 $xx$ $x$ .

파슈의 공리: $(Bxuz\land Byvz)\오른쪽 화살표 \exists a\, (Buay\land Bvax)}$

연속성: φ과 ψ은 광선을 두 반반으로 나누고, 공리는 두 반반으로 나누어진 점 b의 존재를 주장한다.

연속성의 공리 스키마

φ(x)와 ψ(y)를 a 또는 b의 자유로운 인스턴스(instance)가 없는 1차 주문 공식이 되게 한다. 또한 ψ(y)에는 x가, φ(x)에는 y가 없는 경우로 한다. 그러면 다음과 같은 스키마의 모든 인스턴스가 공리다.

\displaystyle \exists a\,\all x\,\forall y\,[(\phi (x)\land \psi (y)\rightarrow Baxy]\rightarrow \exists b\,\forall y\,[\phi (x)\land \psi)\rig)\righrow Bxby.}

r을 끝점 a가 있는 광선이 되게 하라. 첫 번째 순서인 φ과 ψ은 r의 하위 집합 X와 Y를 정의하여 Y의 모든 포인트가 X의 모든 포인트(a에 대하여)의 오른쪽에 오도록 한다. 그리고 X와 Y 사이에 r에 b 점이 있다. 이것은 본질적으로 디데킨드 절단 시공으로, 세트에 걸쳐 정량화를 피하는 방식으로 수행된다.

하단 치수: $\displaystyle \exists a\, \exists b\, \exists c\, \neg Babc\land \neg Bbca\land \neg Bcab.}$

세 가지 비협조적인 점이 있다. 이 공리가 없다면 이론은 1차원 실선, 단점, 심지어 빈 집합에 의해 모델링될 수 있을 것이다.

화합과 중간

상부 치수

상부 치수: $#\displaystyle (xu\equiv xv)\land (yu\equiv yv)\land (zu\equq zv)\land (u\neq v)\rightarrow (Bxyz\lor Byzx\lor Bzxyxy)\lor Bzxy.}$

두 개의 뚜렷한 점에서 등거리인 세 점이 선을 이룬다. 이 공리가 없다면 이론은 3차원 공간이나 더 높은 차원의 공간에 의해 모델링될 수 있을 것이다.

유클리드 공리

이 공리의 세 변형은 각각 유클리드 평행 가설의 나머지 타르스키 공리에 상당하며 다른 공리에 비해 이점이 있다.

실존적 정량자가 있는 경우
B는 변수 및 원자 문장이 가장 적다.
C는 단지 하나의 원시적인 관념, 중간을 필요로 한다. 이 변종은 문헌에서 흔히 볼 수 있는 것이다.

A:

{\displaystyle ((Bxyw\land xy\equiv yw)\land (Bxuv\land xu\equiv uv)\land (Byuz\land yu\equiv zu))\rightarrow yz\equiv vw.

}

선 세그먼트를 주어진 삼각형의 두 변의 중간점과 결합하도록 한다. 그 선 부분은 제3면보다 절반 길어질 것이다. 이것은 두 개의 직각으로 합한 삼각형의 내부 각도와 동등하다.

B:

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

x x

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

x x

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

(

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

a

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

y

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

z a

Bxyz\lor Byzx\lor Bzxy\lor \exists a\,(xa\equiv ya\land xa\equiv za).

) .

{\displaystyle Box\lor Bzx\lor Bzxx\lor

Bzxy\lor

\exists a\,

(

xa\equiv ya\land

x\

equiv za)

}

어떤 삼각형이라도 주어진다면, 모든 정점을 포함하는 원이 존재한다.

유클리드 공리: c

C:

{\displaystyle (Bxuv\land Byuz\land x\neq u)\rightarrow \exists a\,\exists b\,(Bxya\land Bxzb\land Bavb).

}

내부에는 어떤 각도와 어떤 점 v가 주어지면 각도의 양쪽에 끝점이 있는 v를 포함한 선 세그먼트가 존재한다.

5개 세그먼트

5개 세그먼트

(x\neq y\land Bxyz\land Bxyz\land xy'\equiv xy'\land yz\equiv yz'\land shu\equiv yu')}\rightarrow zu\equiv z'u'u.'}

처음에는 두 삼각형, 즉 Xuz와 X'u'z로 시작한다. 각 삼각형의 꼭지점을 정점 반대편의 점으로 연결한 선 세그먼트 yu와 y'u'를 그린다. 결과는 각각 5개의 세그먼트로 구성된 2개의 분할된 삼각형이다. 한 삼각형의 네 개의 세그먼트가 다른 삼각형의 세그먼트에 각각 합치되는 경우, 두 삼각형의 다섯 번째 세그먼트가 합치되어야 한다.

This is equivalent to the side-angle-side rule for determining that two triangles are congruent; if the angles uxz and u'x'z' are congruent (there exist congruent triangles xuz and x'u'z'), and the two pairs of incident sides are congruent (xu ≡ x'u' and xz ≡ x'z'), then the remaining pair of sides is also congruent (uz ≡ u'z').

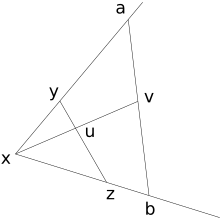
세그먼트 구성: $\displaystyle \exists z\,[Bxyz\land yz\equiv ab]}$

임의의 지점 y에 대해, 어떤 방향(x에 의해 결정됨)으로 어떤 세그먼트 ab에 결합된 선을 그릴 수 있다.

토론

지점이 밀집한 우주인 두 원시적 관계에서 출발하여 타르스키는 선 세그먼트의 기하학을 구축했다. 타르스키와 기반트(1999: 192-93)에 따르면 위의 공리 중 근본적으로 새로운 공리는 하나도 없다고 한다. 처음의 네 개의 공리는 두 원시 관계의 몇 가지 기본적인 성질을 확립한다. 예를 들어, Congrence의 반사율과 Transitability는 결합이 라인 세그먼트에 걸친 동등성 관계라는 것을 확립한다. 그 관계가 불분명한 점에 적용될 때, 일치의 아이덴티티와 사이의 아이덴티티는 사소한 경우를 지배한다. xy≡z £ x=y £ bxx는 이러한 신분 공리를 확장하고 있다.

다음과 같은 이론으로 중간성의 많은 다른 특성들을 도출할 수 있다.

반사율: Bxxy ;
대칭: Bxyz → Bzyx ;
전이성: (Bxyw xy Byzw) → Bxyz ;
연결성: (Bxyw ∧ Bxzw) → (Bxyz ∨ Bxzy).

마지막 두 속성은 선 세그먼트를 구성하는 점들을 완전히 정렬한다.

상부 및 하부 치수는 이러한 공리의 어떤 모델도 특정한 유한 치수성을 가질 것을 요구한다. 이러한 공리의 적절한 변경은 치수 0, 1 및 2보다 큰 유클리드 기하학에 대한 공리 세트를 산출한다(Tarski 및 Givant 1999: 공리⁽¹⁾ 8, 8⁽ⁿ⁾, 9⁽⁰⁾, 9⁽ⁿ⁾, 9⁽¹⁾ . 솔리드 형상은 힐버트의 공리가 있는 경우와 달리 새로운 공리를 필요로 하지 않는다는 점에 유의한다. 더욱이, n 치수에 대한 하위 치수는 단순히 n - 1 치수에 대한 상위 치수의 부정일 뿐이다.

치수 수가 1보다 클 경우, 일치성의 관점에서 Betweenness를 정의할 수 있다(Tarski and Givant, 1999). 먼저 관계 "d"를 정의하십시오( $ab\leq cd$ b c $ab\leq cd$ $ab\leq cd$ 이(가 $ab\leq cd$ ) " $b$ $ab$ 이(가 $)$ 선 세그먼트 $길이$ c $d$ {\ $displaystyle cd}$ 보다 $cd$ 작거나 같음 $ab$ ).

\displaystyle xy\leq zu\왼쪽 오른쪽 화살표 \forall v(zv\equiv uv\rightarrow \w(xw\equiv yw\land yw\equiv uv)).}

2차원의 경우 직관은 다음과 같다. 모든 선 세그먼트 xy의 경우 xv의 가능한 길이 범위를 고려하십시오. 여기서 v는 xy의 수직 이등분선에 있는 임의의 점입니다. xv 길이에 대한 상한은 없지만, v가 xy의 중간점일 때 발생하는 하한은 분명히 있다. 따라서 xy가 zu보다 짧거나 같으면 xv의 가능한 길이 범위는 zw의 가능한 길이 범위의 superset이 될 것이다. 여기서 w는 zu의 수직 이등분선에 있는 어떤 지점이다.

그 다음 두 점 사이의 가장 짧은 거리가 직선이라는 직관을 사용하여 간격을 정의할 수 있다.

\displaystyle Bxyz\왼쪽 오른쪽 화살표 \forall u(ux\leq xy\land uz\leq zy)\오른쪽 화살표 u=y.}

Axiom Schema of Continuity는 선상의 포인트 순서가 완료되었음을 보장한다(최초 순서의 정의 가능한 속성과 관련). 파슈와 유클리드 의 악시오스는 잘 알려져 있다. 놀랍게도 유클리드 기하학에는 다음과 같은 추가 공리가 필요하다.

세그먼트 구성. 이 공리는 측정과 데카르트 좌표계를 가능하게 한다. 단순히 1의 값을 임의의 비어 있지 않은 선 세그먼트에 할당한다.^{[clarification needed]}

wff는 기초 기하학의 잘 형성된 공식(또는 구문론적으로 정확한 공식)을 나타내도록 한다. 타르스키와 기반트(1999: 175)는 기초 기하학이 다음과 같은 것임을 증명했다.

일관성: 그것과 그것의 부정은 모두 이론일 뿐이라는 것은 없다.
완료: 모든 문장 또는 그 부정은 공리로부터 증명할 수 있는 정리다.
해독 가능: 모든 문장에 진실값을 할당하는 알고리즘이 존재한다. 타르스키의 말에서 다음과 같은 내용이 나온다.
- 정량화 제거(Tarski-Seidenberg 정리)를 통해 발견한 실제 폐쇄 영역에 대한 의사결정 절차
- 공리는 (다차원) 충실한 해석을 실제 폐쇄된 영역으로 인정하는 것이다.

굽타(1965)는 위의 공리를 독립적으로 증명했고, 파슈와 콩그루엔스의 반사성을 제외했다.

유클리드 공리를 부정하면 쌍곡 지오메트리가 생성되는 반면 완전히 제거하면 절대 지오메트리가 생성된다. 전체(초급과는 반대로) 유클리드 기하학은 1차 순서 공리화를 포기해야 한다: 연속성의 공리 스키마에서 ranging(x)와 ψ(y)를 x ∈ A와 y ∈ B로 대체한다. 여기서 A와 B는 점 집합에 걸쳐 범용적으로 정량화된 변수다.

힐버트와의 비교

힐베르트의 평면 기하학 번호 16에 대한 공리학, Transitability of Congrence 와 Axiom of Pasch를 포함한다. 이 발언에서 타르스키의 공리에 대해 언급된 직관적 기하학에서 유일한 개념은 삼각형이다. (유클리드 악시오름의 대열 B와 C는 각각 "원"과 "각도"를 가리킨다. 힐버트의 공리는 또한 "레이", "각도" 그리고 삼각형의 "각도"를 필요로 한다. 힐베르트의 공리는 중간성과 일치성 외에도 점과 선을 연결하는 원시적인 이진 관계인 "on"을 필요로 한다. 연속성의 악시오름 스키마는 힐버트의 연속성의 두 가지 공리와 비슷한 역할을 한다. 이 스키마는 없어서는 안 된다; 타르스키(또는 동등한) 언어의 유클리드 기하학은 1차 이론으로서 정밀하게 공리화 될 수 없다. 힐버트의 공리는 그의 연속성 공리에는 2차적 논리가 필요하기 때문에 1차적 이론에 해당하지 않는다.

평면 기하학에 대한 힐베르트의 공리의 처음 4개 그룹은 타르스키의 공리에서 연속성을 뺀 것으로 바이 해석할 수 있다.

참고 항목

메모들

^ 타르스키와 기반트, 1999, 177페이지

참조

Franzén, Torkel (2005), Gödel's Theorem: An Incomplete Guide to Its Use and Abuse, A K Peters, ISBN 1-56881-238-8
지반트, 스티븐(1999) "알프레드 타르스키의 작품에서 실을 통일한다", 수학 인텔리전서 21:47–58.
Gupta, H. N. (1965) 자칭 기하학 기초에 대한 기여. 캘리포니아-버클리 대학의 박사 논문.
타르, 알프레드(1959년),"어느 초등 기하학은?", 레온 Henkin, 패트릭 Suppes과 타르 스키(교육.), 그 공리적 방법에서.기하학과 물리학에 특별한 참조입니다.국제 공동 학술 대회 논문집은 대학교에서. 캘리포니아, 버클리, 12월 26일 1957-Jan의 4,1958년, 논리에 연구로, 수학, 암스테르담의 기초의:를 열었다.North-Holland, pp. 16–29, MR0106185.2007년 재판, 브라우어 출판부, 아이 에스비엔 1-4437-2812-8로 이용 가능합니다.
Tarski, Alfred; Givant, Steven (1999), "Tarski's system of geometry", The Bulletin of Symbolic Logic, 5 (2): 175–214, CiteSeerX 10.1.1.27.9012, doi:10.2307/421089, ISSN 1079-8986, JSTOR 421089, MR 1791303
슈바브호이저, W, 스스미엘류, 1983년 알프레드 타르스키. Metamatische Metahmatische Methoden in der Geomet 스프링거-베를라크.
Szczerba, L. W. (1986). "Tarski and Geometry". Journal of Symbolic Logic. 51 (4): 907–12. doi:10.2307/2273904. JSTOR 2273904.

[1] 타르스키와 기반트, 1999, 177페이지

[1]

Search