사면체-팔면체 벌집
Tetrahedral-octahedral honeycomb| 교대입방형 벌집 | |
|---|---|
  | |
| 유형 | 균일한 벌집 |
| 가족 | 교대 고입방체 벌집 심플렉틱 벌집 |
| 색인화[1] | J21,31,51, A2 W9, G1 |
| 슐레플리 기호 | h{4,3,4} {3[4]} ht0,3{4,3,4} h{4,4}h{filename} ht0,2{4,4}h{filename} h{caps}h{caps}h{caps} s { seconds }s { seconds }s { seconds } |
| 콕서터 도표 | |
| 셀 | {3,3} {3,4} |
| 얼굴 | 삼각형 {3} |
| 엣지 | [{3,3}.{3,4}]2 (표준) |
| 꼭지점 도형 |  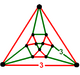  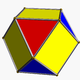 (6팔면체) |
| 대칭군 | Fm3m (225) |
| 콕서터군 | ~ 스타일 [4,31,1] |
| 듀얼 | 도데카헤드리유 마름모꼴 12면체 벌집 셀: |
| 특성. | 정점 전이, 가장자리 전이, 준규칙 벌집 |
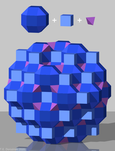
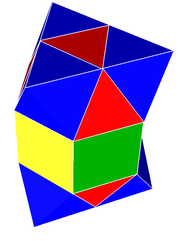
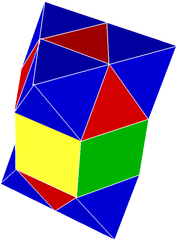
사면체-팔면체 벌집, 교대 입방체 벌집은 유클리드 3-공간에서 준규격 공간 채우기 테셀레이션(또는 벌집)이다.그것은 1:2의 비율로 정팔면체와 정팔면체를 번갈아 가며 구성되어 있다.
다른 이름으로는 반입방체 벌집, 반입방체 세포화, 또는 사방정방체 세포화 등이 있다.존 호튼 콘웨이는 이 벌집을 테트로크타헤드리유라고 부르고, 이중으로 도데카헤드리유라고 부릅니다.
R. Buckminster Fuller는 8면체와 4면체의 두 단어를 하나의 8면체(또는 두 개의 정사각형 피라미드)와 두 개의 반대 4면체로 구성된 마름모꼴인 8면체로 결합합니다.
각 정점 주위에 8개의 사각형과 6개의 팔각형으로 정점-추이적입니다.각 모서리에 2개의 사면체와 2개의 8면체가 번갈아 가면서 모서리-추이적입니다.
기하학적 벌집이란 다면체 이상의 고차원 셀을 공간 충전하여 틈이 없도록 하는 것입니다.이것은 임의의 수의 차원에 대한 보다 일반적인 수학적 타일링 또는 테셀레이션의 예입니다.
허니콤은 보통 볼록한 균일한 벌집처럼 평범한 유클리드("평탄한") 공간에서 만들어집니다.그것들은 또한 쌍곡선 균일한 벌집과 같은 비유클리드 공간에서도 구성될 수 있다.어떤 유한 균일한 폴리토프도 그 원주면에 투영되어 구면 공간에 균일한 벌집을 형성할 수 있다.
이것은 고입방체 벌집의 교대로 형성되고 데미하이퍼큐브와 교차 폴리토프 면으로 구성된, 교대 고입방체 벌집이라고 불리는 무한한 균일한 벌집군의 일부입니다.그것은 또한 심플렉틱 허니콤이라고 불리는 또 다른 무한한 균일한 허니콤 과의 일부이다.
이 3공간에서는 입방체 벌집을 교대로 하여 입방체 셀을 사면체로 환원하고, 삭제된 정점은 8면체 공간을 형성한다.따라서 확장 슐레플리 기호 h{4,3,4}는 {4,3,4}입방 벌집의 정점의 절반을 포함하는 것으로 나타낼 수 있습니다.
회전하는 사면체-팔면체 벌집이라고 불리는 유사한 벌집이 있는데, 이 벌집은 층이 60도 회전하여 모서리의 절반이 사면체와 팔면체를 번갈아 가지는 대신 인접해 있습니다.
사면체-팔면체 벌집은 사면체와 팔면체로 이루어진 불균일한 벌집을 만들어 팔면체 세포에 사면체를 배치함으로써 대칭을 배가시킬 수 있다.그것의 꼭지점 도형은 3차 잘린 삼면체이다.이 벌집은 삼면체 절단된 사면체 벌집 중 이중으로 삼면체 절단된 사면체 세포를 가지고 있습니다.
데카르트 좌표
모서리가 축에 평행하고 모서리 길이가 1인 교대 입방체 벌집의 경우 정점의 데카르트 좌표는 다음과 같습니다(모든 정수 값에 대해 i,j,k with i+j+k).
- (i, j, k)

대칭
2개의 반사구조와 많은 교대입방형 벌집구조가 있습니다. 예:
| 대칭 | ~ 스타일 [4,31,1] = ~ 3 { style {_ {3} , [ 1, 4, 3, 4 ] | ~ 3( 스타일 [3[4]] = ~ 3 ( \ {}{} ) 、 [ 11,1, 4, 3+ ] | [(4,3,4,2+)] | [(4,3,4,2+)] |
|---|---|---|---|---|
| 스페이스 그룹 | Fm3m (225) | F43m (216) | I43m (217) | P43m (215) |
| 이미지 | 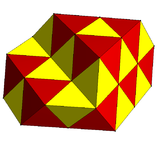 |  | ||
| 사면체의 종류 | 1 | 2 | 3 | 4 |
| 콕서터 도표 |
큐빅 벌집 슬라이스 교대로 사용
교대된 큐빅 벌집을 단면으로 잘라 팔면체 내부에서 새로운 정사각형 면을 만들 수 있습니다.각 조각은 위쪽과 아래쪽을 향한 정사각형 피라미드와 모서리에 있는 사면체를 포함합니다.두 번째 슬라이스 방향은 새로운 면을 필요로 하지 않으며, 4면체와 8면체를 번갈아 포함한다.이 슬래브 벌집은 균일한 세포가 없기 때문에 균일한 것이 아니라 비늘 모양의 벌집이다.
 |  |
접어서 투영
한 쌍의 거울을 서로 매핑하는 기하학적 접기 연산을 통해 교대 입방체 벌집을 평면 사각형 타일링에 직교 투영할 수 있습니다.교대 입방체 벌집 투영으로 평면의 정사각형 타일링 정점 배열에 대한 두 개의 간격띄우기 복사본이 생성됩니다.
| 콕서터 그룹. | ||
|---|---|---|
| 콕서터 도표 | ||
| 이미지 |  |  |
| 이름. | 교대 입방 벌집 | 정사각형 타일링 |
A3/D3 격자
정점 배열은 A 격자 또는3 D [2][3]격자를 나타냅니다3.이 격자는 결정학에서는 면중심 입방체 격자로 알려져 있으며, 정점이 가능한 한 가장 높은 평균 밀도를 달성하는 동일한 구를 가진 밀착형 격자 중심이기 때문에 입방체 밀착형 격자라고도 불립니다.사면체-팔면체 벌집은 심플렉틱 벌집의 3차원 케이스이다.그것의 보로노이 셀은 마름모꼴 12면체로, 4옥트 벌집을 위한 정육면체 도형의 쌍대이다.
D+
3 패킹은 2개의3 D(또는3 A) 격자를 결합하여 구성할 수 있습니다.D+
n 패킹은 짝수 치수에 대한 격자일 뿐입니다.키스수는 2=4(nn-1<8의 경우 2, n=8의 경우 240, n>[4]8의 경우 2n(n-1))이다2.




 ∪
∪ 




A 또는*
3 D 격자(A 또는4
3 D라고도 함4
3)는*
3 4개의3 모든 A 격자의 결합에 의해 구성될 수 있으며, 균일한 비트런 큐빅 벌집인 디셰노이드 사면체 벌집,[5] 이중 벌집의 정점 배열과 동일합니다.그것은 또한 체심 입방체이며, 두 입방체 벌집이 이중 위치에 결합되어 있습니다.




 = = = dual of = dual of = 。
= = = dual of = dual of = 。
D*
3 격자의 키스 수는 8이고[6], 그것의 보로노이 테셀레이션은 모든 잘린 팔면체 보로노이 세포를 포함하는 비트런치 큐빅 벌집이다.[7]
관련 벌집
C3 벌집
[4,3,4], , 콕서터 그룹은 교대로 입방체 벌집을 포함한 뚜렷한 형상을 가진 15개의 균일한 벌집을 생성한다.확장된 큐빅 벌집(런케이트된 큐빅 벌집이라고도 함)은 큐빅 벌집과 기하학적으로 동일합니다.
| C3 벌집 | |||||
|---|---|---|---|---|---|
| 공간 그룹. | 파이브리폴드 | 확장된 대칭 | 확장된 도표 | 주문 | 허니콤 |
| PM3m (221) | 4−:2 | [4,3,4] | ×1 | | |
| FM3m (225) | 2−:2 | [1+,4,3,4] ↔ [4,31,1] | ↔ | 반 | |
| I43m (217) | 4o:2 | [(4,3,4,2+)] | 반×2 | ||
| Fd3m (227) | 2+:2 | [1+,4,3,4,1+] ↔ [3[4]] | ↔ | 분기 × 2 | |
| 임3m (229) | 8o:2 | [[4,3,4]] | ×2 | ||
B3 벌집
[4,31,1], , 콕서터 그룹은 교대 입방체 벌집을 포함한 뚜렷한 형상을 가진 균일한 벌집 9개의 순열을 생성한다.
| B3 벌집 | |||||
|---|---|---|---|---|---|
| 공간 그룹. | 파이브리폴드 | 확장된 대칭 | 확장된 도표 | 주문 | 허니콤 |
| FM3m (225) | 2−:2 | [4,31,1] ↔ [4,3,4,1+] | ↔ | ×1 | |
| FM3m (225) | 2−:2 | <[1+,4,31,1]> ↔ <[3[4]]> | ↔ | ×2 | |
| PM3m (221) | 4−:2 | <[4,31,1]> | ×2 | ||
A3 벌집
이 벌집은 A디스플레이 _ 콕서터 이 만든 5개의 균일한 벌집[8] 중 하나입니다.대칭은 Coxeter-Dynkin 다이어그램에서 링의 대칭으로 곱할 수 있습니다.
| A3 벌집 | ||||||
|---|---|---|---|---|---|---|
| 공간 그룹. | 파이브리폴드 | 광장 대칭 | 확장된 대칭 | 확장된 도표 | 확장된 그룹. | 벌집 도표 |
| F43m (216) | 1o:2 | a1 | [3[4]] | (없음) | ||
| FM3m (225) | 2−:2 | d2 | <[3[4]]> ↔ [4,31,1] | ↔ | ~ 3( 스타일 × 21 ↔ ~ 스타일 {3} | |
| Fd3m (227) | 2+:2 | g2 | [3[4]] 또는 [2+[3[4]] | ↔ | ~ 3( 스타일 × 22 | |
| PM3m (221) | 4−:2 | d4 | <2[3[4]]> ↔ [4,3,4] | ↔ | ~ 3( 스타일 × 41 ↔~ 3( {3}) | |
| I3 (204) | 8개−o | r8 | [4[3[4]]+ ↔ [[4+,3,4] | ↔ | A {38 ↔ ~ 3 { style { _3}} × 2 | |
| 임3m (229) | 8o:2 | [4[3[4]] ↔ [[4,3,4]] | ~ 3( 스타일 × 8 ↔~332 | |||
준규격 벌집
| 준규격 폴리코라 및 벌집: h{4,p,q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 공간 | 유한 | 아핀 | 작은 | 파라콤팩트 | |||||||
| 슐레플리 기호. | h{4,3,3} | h{4,3,4} | h{4,3,5} | h{4,3,6} | h{4,4,3} | h{4,4,4} | |||||
| 콕서터 도표 | |||||||||||
| 이미지 |  |  |  |  | |||||||
| 꼭지점 수치 r{p,3} |  |  |  |  |  |  | |||||
캔틱 큐빅 벌집
| 캔틱 큐빅 벌집 | |
|---|---|
| 유형 | 균일한 벌집 |
| 슐레플리 기호 | h2{4,3,4} |
| 콕서터 도표 | |
| 셀 | t{3,4} r{4,3} t{3,3} |
| 얼굴 | 삼각형 {3} 제곱 {4} 육각형 {6} |
| 꼭지점 도형 |  직사각형 피라미드 |
| 콕서터 군 | [4,31,1], ~ 3({ [3[4]], |
| 대칭군 | Fm3m (225) |
| 듀얼 | 반원형 옥타헤드리유 셀: |
| 특성. | 정점 전이성의 |
캔틱 입방체 벌집, 캔틱 입방체 셀레이션 또는 잘린 반입방체 벌집은 유클리드 3-공간에서 균일한 공간 채우기 테셀레이션(또는 벌집)이다.이것은 1:1:2의 비율로 잘린 8면체, 큐빅타헤드라, 잘린 4면체로 구성되어 있다.그것의 꼭지점 도형은 직사각형 피라미드이다.
존 호튼 콘웨이는 이 벌집을 잘린 테트라옥타헤드리유라고 부르고 이중 반원형 옥타헤드리유라고 부릅니다.
대칭
그것은 두 개의 다른 균일한 구조를 가지고 있다.디스플레이 구조는 색상의 잘린 사각형으로 번갈아 볼 수 있습니다.
| 대칭 | [4,31,1], ~ 3({ =<[3[4]]> | [3[4]], |
|---|---|---|
| 스페이스 그룹 | Fm3m (225) | F43m (216) |
| 색칠 |  | 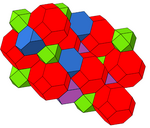 |
| 콕서터 | ||
| 꼭지점 도형 |  | 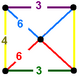 |
관련 벌집
그것은 통조림 큐빅 벌집과 관련이 있다.마름모꼴은 잘린 팔면체로, 입방체는 잘린 사면체로 환원된다.
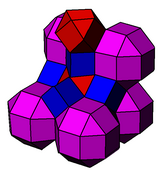 캔텔화 입방체 |  칸트 입방체 |
rr{4,3}, r{4,3}, {4,3} | t{3,4}, r{4,3}, t{3,3} |
룬식 큐빅 벌집
| 룬식 큐빅 벌집 | |
|---|---|
| 유형 | 균일한 벌집 |
| 슐레플리 기호 | h3{4,3,4} |
| 콕서터 도표 | |
| 셀 | rr{4,3} {4,3} {3,3} |
| 얼굴 | 삼각형 {3} 제곱 {4} |
| 꼭지점 도형 | 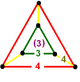 삼각 좌골 |
| 콕서터군 | ~4 ( 스타일 [4,31,1] |
| 대칭군 | Fm3m (225) |
| 듀얼 | 쿼터 큐빌 셀: |
| 특성. | 정점 전이성의 |
런시 큐빅 벌집 또는 런시 큐빅 셀레이션은 유클리드 3-공간에서 균일한 공간 채우기 테셀레이션(또는 벌집)입니다.그것은 마름모꼴, 큐브, 사면체로 1:1:2의 비율로 구성되어 있다.그것의 꼭지점 도형은 삼각형 좌골이며, 한쪽 끝은 사면체, 반대쪽 끝은 입방체, 사다리꼴 변은 세 개의 마름모꼴이다.
존 호튼 콘웨이는 이 벌집을 3-RCO-트릴이라고 부르고, 이중 1/4 큐빌이라고 부릅니다.
쿼터 큐빌
Runcic 큐빅 벌집 2개를 Quarter cubille이라고 하며, Coxeter 다이어그램에서는 4(\ [4,31,1] 기본 영역의 4개 중 2개에 면이 있습니다.
셀은 4개의 정점과 중심을 사용하여 절개된 큐브의 1/4로 볼 수 있습니다.6개의 가장자리 주위에 4개의 셀이 있고 3개의 가장자리 주위에 3개의 셀이 있습니다.
관련 벌집
이것은 입방체의 4분의 1이 사면체로 교체되고 절반은 마름모꼴로 확장되는 룬케이티드 큐빅 벌집과 관련이 있다.
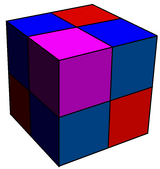 런케이티드 큐빅 |  룬치 입방체 |
| {4,3}, {4,3}, {4,3}, {4,3} | h{4,3}, rr{4,3}, {4,3} |
이 벌집은 잘린 정사각형 타일 평면으로 나눌 수 있으며, 마름모꼴의 팔각형 중심을 사용하여 정사각형 큐폴레를 만들 수 있습니다.이 스칼라 모양의 벌집 모양은 콕서터 다이어그램과 기호3 s{2,4,4}로 표현되며, 콕서터 표기 대칭은+ [2,4,4]이다.
런시칸틱 큐빅 벌집
| 런시칸틱 큐빅 벌집 | |
|---|---|
| 유형 | 균일한 벌집 |
| 슐레플리 기호 | h2,3{4,3,4} |
| 콕서터 도표 | |
| 셀 | tr{4,3} t{4,3} t{3,3} |
| 얼굴 | 삼각형 {3} 제곱 {4} 육각형 {6} 팔각형 {8} |
| 꼭지점 도형 | 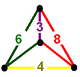 거울상 구상체 |
| 콕서터군 | ~4 ( 스타일 [4,31,1] |
| 대칭군 | Fm3m (225) |
| 듀얼 | 반피라미딜 셀: |
| 특성. | 정점 전이성의 |
런시칸틱 큐빅 벌집 또는 런시칸틱 큐빅 셀레이션은 유클리드 3공간에서 균일한 공간을 채우는 테셀레이션(또는 벌집)이다.이것은 1:1:2의 비율로 잘린 정육면체, 잘린 정육면체, 잘린 정육면체로 구성되어 있으며, 대칭된 구형 정점 도형을 가지고 있다.그것은 룬시칸텔이 있는 큐빅 벌집과 관련이 있다.
존 호튼 콘웨이는 이 벌집을 f-tco-tille이라고 부르고 이중 반 피라미드라고 부릅니다.
하프피라미딜
콕서터 다이어그램과 함께 런시트화된 입방체 벌집과 쌍수를 하프 피라미딜이라고 합니다.얼굴은 [4,31,1], ~ Coxeter 그룹의 4개 하이퍼플레인 중 3개에 존재한다.
셀은 불규칙한 피라미드이며 큐브의 1/12 또는 마름모꼴 12면체의 1/24로 볼 수 있으며, 각 셀은 3개의 모서리와 큐브의 중심으로 정의됩니다.
관련 스큐 아페이로헤드라
정점 배열이 동일하지만 삼각형과 정사각형이 제거된 균일한 편면체가 존재합니다.이것은 잘린 사각형과 잘린 정육면체가 함께 증강된 것으로 볼 수 있다.
관련 벌집
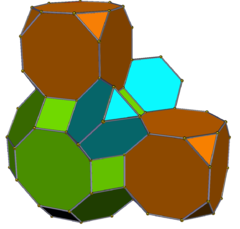 런시칸틱 큐빅 |  룬시칸텔화 입방체 |
회전식 사면체-팔면체 벌집
| 회전식 사면체-팔면체 벌집 | |
|---|---|
| 유형 | 볼록 균일한 벌집 |
| 콕서터 도표 | |
| 슐레플리 기호 | h{4,3,4:g h{6,3}h{filename} s{3,6}h{param} s{3[3]}h{filename} |
| 셀 | {3,3} {3,4} |
| 얼굴 | 삼각형 {3} |
| 꼭지점 도형 |  삼각 직소성 우산 G3.4.3.4 |
| 스페이스 그룹 | P63/mmc(194) [3,6,2+,2] |
| 듀얼 | 트라페조롬브 12면체 벌집 |
| 특성. | 정점 전이성의 |
회전 사면체-팔면체 벌집 또는 회전식 교대 입방체 벌집은 1:2의 비율로 8면체와 4면체로 이루어진 유클리드 3공간의 공간을 채우는 테셀레이션(또는 벌집)이다.
각 정점 주위에 8개의 사각형과 6개의 팔각형으로 정점이 균일합니다.
가장자리가 균일하지 않습니다.모든 모서리에는 2개의 사면체와 2개의 팔면체가 있지만, 어떤 모서리는 교대로 있고 어떤 모서리는 쌍으로 되어 있습니다.
이 층은 벌집 모양의 반사층으로 볼 수 있습니다.
 |
회전에 의한 시공
이것은 또 다른 벌집인 사면체-팔면체 벌집의 대칭성이 떨어지는 버전입니다. 벌집에서는 각 가장자리가 사면체와 팔면체로 둘러싸여 있습니다.둘 다 두께가 1셀인 레이어로 구성되며, 그 안에서 두 종류의 셀이 엄밀하게 번갈아 이루어집니다.이들 층을 분리하는 평면상의 면은 삼각형의 규칙적인 패턴을 형성하기 때문에 인접한 층은 한 층의 각 8면체가 다음 층의 사면체와 만나거나 각 셀이 같은 종류의 셀과 만나도록 배치될 수 있다(따라서 층 경계는 반사면이 된다).후자의 형태는 회전율이라고 불립니다.
정점 도형은 삼각형 직교소성 우폴라라고 불리며, 그 정점 도형은 낮은 대칭의 정점 도형이 삼각형 자이로비쿠폴라라고 불리며, 따라서 자이로 접두사는 쓰임새가 역전된다.
| 벌집 | 회전 테트옥트 | 반사 테옥트 |
|---|---|---|
| 이미지 | 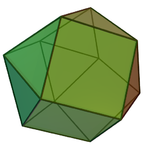 |  |
| 이름. | 삼각 직소성 우산 | 삼각 자이로비쿠폴라 |
| 꼭지점 도형 | 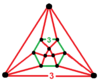 | 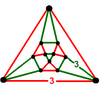 |
| 대칭 | D3h, 주문 12 | D3d, 주문 12 (Oh, 명령 48) |
교대로 시공
지오메트리는 육각형 프리즘 벌집에 적용되는 교대 연산을 사용하여 구성할 수도 있습니다.육각형 프리즘 세포는 8면체가 되고, 그 구멍은 이 벌집의 사면체 쌍으로 나눌 수 있는 삼각쌍뿔을 만듭니다.이 두 개의 정육면체를 가진 벌집을 디테트라헤럴-팔면체 벌집이라고 합니다.Coxeter-Dynkin 다이어그램은 3가지이며, 1색, 2색 또는 1, 2, 또는 3가지 색상으로 볼 수 있습니다.
자이로롱게이트 큐빅 벌집
| 자이로롱게이트 큐빅 벌집 | |
|---|---|
| 유형 | 균일한 벌집 |
| 슐레플리 기호 | h{4,3,4: ge {3,6}h1{filename} |
| 콕서터 다이어그램 | |
| 셀 | {3,3} {3,4} (3.4.4) |
| 얼굴 | 삼각형 {3} 제곱 {4} |
| 꼭지점 도형 |  |
| 스페이스 그룹 | P63/mmc(194) [3,6,2+,2] |
| 특성. | 정점 전이성의 |
자이로 연동된 대체 입방체 벌집 또는 가늘고 긴 삼각 반마모 세포화는 유클리드 3공간의 공간을 채우는 테셀레이션(또는 벌집)이다.그것은 1:2:2의 비율로 팔면체, 삼각 프리즘, 사면체로 구성되어 있다.
각 정점 주위에 3개의 8면체, 4개의 4면체, 6개의 삼각형 프리즘이 있는 정점-추이적입니다.
길쭉한 교대 입방체 벌집은 각 정점에서 셀 배열이 동일하지만 전체 배열은 다릅니다.길쭉한 형태에서는 각 프리즘이 삼각형 면 중 한 면에서는 사면체와 다른 면에서는 팔면체와 만나고, 자이로융성 형태에서는 프리즘이 양 끝에서 같은 종류의 델타 면과 만난다.
가늘고 긴 큐빅 벌집
| 가늘고 긴 큐빅 벌집 | |
|---|---|
| 유형 | 균일한 벌집 |
| 슐레플리 기호 | h{4,3,4:e {3,6}g1{filename} |
| 셀 | {3,3} {3,4} (3.4.4) |
| 얼굴 | 삼각형 {3} 제곱 {4} |
| 꼭지점 도형 |  이등각뿔에 연결된 삼각 큐폴라 |
| 대칭군 | [6, (3, 2+, 15, 2+)] |
| 특성. | 정점 전이성의 |
길쭉한 교대 입방체 벌집 또는 길쭉한 삼각형 자이로프리즘 셀레이션은 유클리드 3공간에서 공간을 채우는 테셀레이션(또는 벌집)이다.그것은 1:2:2의 비율로 팔면체, 삼각 프리즘, 사면체로 구성되어 있다.
각 정점 주위에 3개의 8면체, 4개의 4면체, 6개의 삼각형 프리즘이 있는 정점-추이적입니다.각 프리즘은 한쪽 끝은 팔면체, 다른 한쪽 끝은 사면체를 만난다.
그것은 각 정점에 같은 배열의 셀을 가진 자이로롱게이트 교대 입방체 벌집이라고 불리는 회전 형태를 가지고 있다.
「 」를 참조해 주세요.
메모들
- ^ 상호 참조를 위해 안드레이니(1-22), 윌리엄스(1-2,9-19), 존슨(11-19, 21-25, 31-34, 41-49, 51-52, 61-65), 그리고 그룬바움(1-28)의 목록 인덱스가 제공됩니다.
- ^ "The Lattice D3".
- ^ "The Lattice A3".
- ^ Conway (1998), 페이지 119
- ^ "The Lattice D3".
- ^ Conway (1998), 페이지 120
- ^ Conway (1998), 페이지 466
- ^ [1], 시퀀스 A000029 6-1 케이스, 0 마크의 경우는 생략
레퍼런스
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (21장, 아르키메데아 및 카탈로니아 다면체와 타일링, 건축학 및 대격 테셀링, 298페이지, 298-2)는 모두 포함되어 있습니다.
- George Olshevsky, Uniform Panoploid Tetracombs, Mancript(2006) (11개의 볼록 균일한 타일링, 28개의 볼록 균일한 벌집, 143개의 볼록 균일한 테트라콤의 전체 목록)
- 브란코 그룬바움, 3공간 균일한 타일링Geombinatorics 4(1994), 49 - 56.
- Norman Johnson 유니폼 폴리토피스, 원고 (1991)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
- Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
- 만화경: H.S.M. 콕서터 선정필, F. 편집자 F.S.M. 콕서터.아서 셔크, 피터 맥멀런, 앤서니 CThompson, Asia Ivic Weiss, Wiley-Intercience Publication, 1995, ISBN978-0-471-01003-6[2]
- (페이퍼 22) H.S.M. 콕서터, 정규 및 준정규 폴리토피스 I, [수학]Zeit. 46(1940) 380–407, MR 2,10] (1.9 균일한 공간 채우기)
- (문서 24) H.S.M. 콕서터, 정규 및 반정규 폴리토피스 III, [수학]Zeit. 200 (1988) 3-45]
- A. Andreini, Sulle reti di poliedri regolari e semirgolari e sulle corrispondi reti 상관관계(다면체의 규칙적 및 반규칙적 그물 및 대응하는 상관관계 그물 위), Mem. Societa Italiana della Sci Scienze, Ser.3, 14(1905) 75–129.
- D. M. Y. Sommerville, n차원 기하학 입문.뉴욕, E. P. Dutton, 1930.196 페이지 (도버출판, 1958년)제 X장: 일반 폴리토피스
- Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9.
외부 링크
- 사각형과 일반 피라미드를 기반으로 한 정사각형으로 만든 건축 디자인. (2003)
- Klitzing, Richard. "3D Euclidean Honeycombs x3o3o *b4o - octet - O21".
- 3공간 균일한 허니콤: 11옥텟
| 공간 | 가족 | 스타일 / 스타일 { / 스타일 | ||||
|---|---|---|---|---|---|---|
| E2. | 균일한 타일링 | {3[3]} | δ3 | 할3 수 있다 | 문제3 | 육각형 |
| E3. | 균일한 볼록한 벌집 | {3[4]} | δ4 | 할4 수 있다 | 문제4 | |
| E4. | 균일한 4-허니콤 | {3[5]} | δ5 | 할5 수 있다 | 문제5 | 24셀 벌집 |
| E5. | 균일한 5벌집 | {3[6]} | δ6 | 할6 수 있다 | 문제6 | |
| E6. | 균일한 6벌집 | {3[7]} | δ7 | 할7 수 있다 | 문제7 | 2개22 |
| E7. | 균일한 7벌집 | {3[8]} | δ8 | 할8 수 있다 | 문제8 | 133 • 331 |
| E8. | 균일한 8벌집 | {3[9]} | δ9 | 할9 수 있다 | 문제9 | 152 • 251 • 521 |
| E9. | 균일한 9벌집 | {3[10]} | δ10 | 할10 수 있다 | 문제10 | |
| E10. | 균일한 10벌집 | {3[11]} | δ11 | 할11 수 있다 | 문제11 | |
| En-1. | 균일한 (n-1)-벌집 | {3[n]} | δn | 할n 수 있다 | 문제n | 1k2 • 2k1 • k21 |