제복4폴리토프

기하학에서 획일적인 4폴리토프(또는 획일적인 폴리초론)^[1]는 4차원 폴리토프로, 그 세포가 획일적인 폴리헤드라이며, 얼굴은 규칙적인 폴리곤이다.

47개의 비프리즘 볼록한 균일 4폴리토프, 1개의 한정된 볼록 프리즘 형태, 2개의 무한 볼록 프리즘 형태가 설명되었다.또한 알 수 없는 수의 비콘벡스 항성 형태도 있다.

발견의 역사

• 볼록형 일반 폴리탑:
  • 1852: 루드비히 슐레플리는 그의 원고인 Theory der Vielfachen Kontinuitét를 통해 4차원에 정확히 6개의 규칙적인 폴리토페가 있고 5차원에 3개밖에 없다는 것을 증명했다.
• 일반 항성 4-폴리톱(별 다면체 세포 및/또는 정점 수치)
  • 1852: 루드비히 슐레플리는 또한 10개의 일반 별 4-폴리탑 중 4개를 발견했는데, 세포나 정점 수치가 {/,⁵₂5}, {5,},⁵₂ {5},/}인 6을 할인했다.
  • 1883: Edmund Hess completed the list of 10 of the nonconvex regular 4-polytopes, in his book (in German) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder [2].
• 볼록 반정형 다상체: (Coxeter의 균일한 범주 이전의 다양한 정의)
  • 1900: 소럴드 고셋은 그의 저서 'n차원 공간의 정규 및 반정규 도표에 관한 연구'에서 정규 세포(플라토닉 고형분)가 있는 비프리즘 반정형 볼록 폴리스토프의 목록을 열거했다.^[2]
  • 1910: 앨리샤 불레 스토트(Alicia Boole Stott)는 그녀의 출판물인 "지오메디컬"에서 일반 폴리토페스와 공간 채움에서 반정형(Semiplicular)을 빼는 것에서도 아르키메데스 고체 및 프리즘 셀을 허용함으로써 정의를 확장했다.이 건설에는 45개의 반경 4-폴리 토플이 열거되어 있다.^[3]
  • 1911:피터 헨드리크 슈테는 정규 폴리에스테르에서 정기적으로 파생되는 폴리에스테르에 대한 분석적 처리를 발표하였고, 5-셀, 8-셀/16셀, 24-셀에 근거한 대칭에 의한 볼록한 균일한 폴리에스테르를 열거하여 Boole-Stott의 공식을 따랐다.
  • 1912: E. L. Elte는 고셋의 목록에 독립적으로 확장되었으며, 출판물 "초음극의 반음극 폴리토페스, 하나 또는 두 종류의 반음극 면을 가진 폴리토페스"가 있다.^[4]
• 볼록한 균일한 폴리탑:
  • 1940년: H.S.M. Coxeter가 출판한 정규 및 준정규 폴리토페스에서 체계적으로 검색을 확장했다.
  • 볼록형 균일 4폴리톱:
    • 1965: 볼록형식의 전체 목록은 마침내 컴퓨터 분석에 의해 확립된 4차원 아르키메데스 폴리토페스 출판물에서 존 호튼 콘웨이와 마이클 가이(Michael Guy)에 의해 열거되었고, 비 와이토피아 볼록스 4폴리토프(Non-Wythofian bol록 4-polytope)만 추가되었다.
    • 1966년 노먼 존슨은 콕시터 고문 휘하의 박사학위 논문 '동일 폴리토페스와 허니컴의 이론'을 완성하고, 4차원 이상에 대한 균일 폴리토페스의 기본 이론을 완성한다.
    • 1986년 Coxeter는 독특한 스너브 24-셀 구조와 변칙적인 대항쟁의 대칭성에 대한 분석을 포함한 논문 정규 및 준정규 폴리토페스 II를 발표했다.
    • 1998^[5]-2000:4 폴리토프는 노먼 존슨에 의해 체계적으로 이름이 지어졌고, 조지 올셰프스키의 온라인 색인 열거에 의해 주어졌다(이 리스트의 기초로 사용됨).존슨은 그리스 뿌리의 폴리("다수")와 초로스("방" 또는 "공간")에서 4폴리탑을 3폴리탑에 대한 폴리헤드라처럼 폴리초라라고 명명했다.^[6]chora)라고 명명했다.균일한 폴리초라의 이름은 Coxeter 다이어그램에 있는 링에 기반한 접두사가 있는 6개의 일반 폴리초라, 잘림_0,1 t, 통음_0,2 t, 런케이트 t_0,3, 수정이라고 불리는 단일 링 형태, 그리고 첫 번째 링이 두 번째 또는 세 번째 노드에 있을 때 bi, tri-prefixes가 추가되었다.^[7][8]
    • 2004: 콘웨이-구이 세트가 완성되었다는 증거는 마르코 뮐러에 의해 그의 논문 비에르디멘탈레 아르키메디스체 폴리토페에 의해 발표되었다.뮐러는 존슨의 호칭 시스템을 자신의 상장에 재현했다.^[9]
    • 2008년:Symmetries Things[10]의 존 H. 콘웨이와 Coxeter 그룹 가족에 의해 각 고리 Coxeter 도표 permutation—snub, 그랜드 antiprism을 위한 충분히 일반적인 vertex 수치 다이어그램과는 볼록 균일 4-polytopes과 고차원의 polytopes의 첫번째print-published 목록이 포함되어 있고 duoprisms—which 그는 proprisms라고 불리는 출판되었다 f또는 동업-roduct 프리즘그는 자신의 ijk-ambo 명명법을 잘림과 비트런시를 넘어 인덱스 링 순열화에 사용했고, 존슨 전 대통령의 이름이 도서 색인에 포함되었다.
• 비정규 균일 별 4-폴리토프: (비콘벡스 균일 다면체와 유사)
  • 1966: Johnson은 논문에서 4칸의 공간에 3개의 비콘벡스 제복 반항을 기술하고 있다.^[11]
  • 1990-2006: 협업 검색에서 2005년까지 조나단 바우어스와 조지 올셰프스키에 의해 총 1845개의 유니폼 4폴리톱스(콘벡스 및 비콘벡스)가 확인되었고,^[12] 2006년에 추가로 4개가 발견되어 총 1849명이 되었다.이 카운트는 비-프리즘적 균일 다면체의 프리즘을 포함하지만(그것은 유한 집합이기 때문에), 무한 범주의 듀오프라임이나 반격의 프리즘은 포함하지 않는다.^[13]
  • 2020년경: 340개의 새로운 폴리초라가 발견되어 알려진 통일 4-제복의 총 수가 2189개로 늘어났다.그 명단은 아직 완결성이 입증되지 않았다.^[13][14]

일반 4폴리탑은 균일한 4폴리탑의 하위집합으로, 추가 요건을 충족한다.일반 4-폴리탑은 Schléfli 기호 {p,q,r}, 유형 {p}, 유형 면 {p}, 모서리 그림 {r} 및 꼭지점 그림 {q,r}을(를) 사용하여 표현할 수 있다.

정규 4 폴리토프 {p,q,r}의 존재는 세포가 되는 정규 다면체 {p,q}과 정점 모양이 되는 {q,r}의 존재에 의해 제약된다.

유한 4 폴리토프로서의 존재는 불평등에 의존한다.^[15]

${\displaystyle \sin \left\frac {}{p}\pi \right)\sin \refac\frace\{r}\cos \left({\frac {}{q}\right).}$

모든 셀, 면, 가장자리 및 꼭지점이 일치하는 16개의 정규 4폴리탑:

• 6개의 일반 볼록볼록 4-셀탑: 5-셀 {3,3,3}, 8-셀 {4,3,3}, 16-셀 {3,4}, 24-셀 {3,4}, 120-셀 {5,3,3}, 600-셀 {3,5}.
• 10정규 스타 4-polytopes:정 20면체 120-cell{3,5,5/2}, 작은stellated120-cell{5/2,5,3}, 위대한 120-cell{5,5/2,5}, 그랜드 120-cell{5,3,5/2}, 위대한stellated 120-cell{5/2,3,5}, 웅장 stellated 120-cell{5/2,5,5/2}, 위대한 웅장한 120-cell{5,5/2,3}, 위대한 정 20면체 120-cell{3,5/2,5}, 그랜드 600-cell{3,3,5/2}, 그리고 훌륭한 거대 120-c stellated.ell{5/2,3,3}.

볼록형 균일 4폴리톱

4차원 균일한 4폴리탑의 대칭

직교 부분군

B의4 16개의 거울은 4A와1 D의4 2개의 직교 그룹으로 분해될 수 있다. = (4개의 미러) = (12개의 거울)

F의4 24개의 거울은 2개의 직교 D4 그룹으로 분해될 수 있다. = (12개의 거울) = (12개의 거울)

B31×A의1 10개의 거울은 직교 그룹인 4A와 D로3 분해될 수 있다. = (3+1 미러) = (6개의 거울)

4차원에는 5가지 기본 미러 대칭점 그룹 패밀리가 있다.A₄ = , B₄ = , D₄ = , F₄₄ = , H = ^[7]. 또한 3개의 프리즘 그룹인₃₁ AA = , BA₃₁ = , HA₃₁ = , 2중주파 그룹인 I₂(p)×I₂(q) = . 거울 평면으로 경계된 구르사트 사면체 기본 영역에 의해 정의된 각 그룹.

각 반사 균일 4 폴리토프는 Coxeter 다이어그램에서 노드 순열 주변의 링으로 대표되는 Wythoff 구성에 의해 4차원 반사 지점 그룹으로 구성될 수 있다.미러 하이퍼플레인은 컬러 노드에서 볼 수 있듯이 짝수 분지로 구분하여 그룹화할 수 있다.[a,b,a] 형태의 대칭 그룹은 대칭이 확장되어 [a,b,a] 대칭 순서를 두 배로 한다.여기에는 [3,3,3], [3,4,3], [p,2,p]가 포함된다.대칭 링이 있는 이 그룹의 균일한 폴리토프는 이 확장된 대칭을 포함한다.

주어진 균일한 폴리토프에서 주어진 색상의 모든 거울이 비링(비활성)되어 있는 경우, 모든 비활성 미러를 제거하여 더 낮은 대칭 구조를 갖게 된다.특정 색상의 모든 노드가 링(활성)된 경우, 교류 연산은 "빈" 원형 노드"로 보이는 치랄 대칭의 새로운 4 폴리토프를 생성할 수 있지만, 일반적으로 기하학적 구조를 조정하여 균일한 솔루션을 만들 수 없다.

바일 무리를 짓다	콘웨이 쿼터니온	추상적 구조화하다	주문	콕시터 도표를 만들다		콕시터 표기법	부분군	콕시터 번호를 붙이다 (h)	m=2h
무레듀케이블
A을4	+1/60[I×I].21	S5	120			[3,3,3]	[3,3,3]+	5		10
D4	±1/3[T×T]2	1/2.2S4	192			[31,1,1]	[31,1,1]+	6		12
B4	±1/6[O×O].2	2S4 = S2≀S4	384			[4,3,3]		8	4	12
F4	±1/2[O×O3].	3.2S4	1152			[3,4,3]	[3+,4,3+]	12	12	12
H4	±[I×I]2	2.(A5×A5).2	14400			[5,3,3]	[5,3,3]+	30		60
프리즘 그룹
A3A1	+1/24[O×O].23	S4×D1	48			[3,3,2] = [3,3]×[ ]	[3,3]+	-		6	1
B3A1	±1/24[O×O].2	S4×D1	96			[4,3,2] = [4,3]×[ ]		-	3	6	1
H3A1	±1/60[I×I]2	A5×D1	240			[5,3,2] = [5,3]×[ ]	[5,3]+	-		15	1
에는 2, 2★★그저(수정의 2,p,2q 사)
I2(p)I2(q)	±1/2[D2p×D2q]	Dp×Dq	4pq			[p,2,q] = [p]×[q]	[p+,2,q+]	-		p	q
I2(2p)I2(q)	±1/2[D4p×D2q]	D2p×Dq	8pq			[2p,2,q] = [2p]×[q]		-	p	p	q
I2(2p)I2(2q)	±1/2[D4p×D4q]	D2p×D2q	16pq			[2p,2,2q] = [2p]×[2q]		-	p	p	q	q

6개의 정규 볼록 4폴리탑을 포함하여 64개의 볼록형 4폴리탑이 있으며, 무한대의 듀오프라임과 반격 프리즘을 제외한다.

• 5는 플라토닉 고형분에 기초한 다면체 프리즘이다(1입방 초프리즘은 큐빅이 큐빅이기 때문에 정규와 겹친다).
• 13은 아르키메데스 고형물에 기초한 다면체 프리즘이다.
• 9는 자기 이중 정규 A₄[3,3,3] 그룹(5-셀) 계열이다.
• 9는 자기 이중 정규 F₄ [3,4,3] 그룹(24-셀) 계열이다. (스너브 24-셀 제외)
• 15는 일반 B₄ [3,3,4] 그룹 (테세락트/16-셀) 계열이다(3은 24-셀 계열과 겹친다)
• 15는 일반 H₄ [3,3,5] 그룹(120-cell/600-cell) 계열이다.
• [3,4,3] 그룹(24-셀) 계열의 특수 스너브 양식 1개.
• 비위토피안 4폴리토페, 대항쟁.
• 총계: 68 - 4 = 64

이 64개의 제복 4폴리토프는 조지 올셰프스키에 의해 아래에 색인을 만들었다.반복된 대칭 형태는 괄호 안에 색인화된다.

위의 64개 외에 나머지 볼록한 형태를 모두 생성하는 2개의 무한 프리즘 집합이 있다.

• 균일한 항정신병 프리즘 집합 - sr{p,2}×{{} - 두 개의 항정신병 프리즘의 다면체 프리즘.
• 균일한 듀오프라임 세트 - {p}×{q} - 두 폴리곤의 데카르트 제품.

A가족₄

5-셀은 정점의 모든 쌍이 동일한 방식으로 연관되어 있기 때문에 순서 120의 디플로이드 펜타코리아[3,3] 대칭이며 5개 원소의 순열과 이형성을 가진다.^[7]

지정된 노드를 제거하여 Coxeter 다이어그램 위치에 그룹화된 팩시트(셀)가 제공된다.

[3,3,3] 균일한 폴리토페스

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수				요소 개수
				포스3길 (5)	포스2길 (10)	양수1길 (10)	양수 0 (5)	세포	얼굴	가장자리	정점
1	5세포 펜타코론[7]		{3,3,3}	(4) (3.3.3)				5	10	10	5
2	교정된 5세포		r{3,3,3}	(3) (3.3.3.3)			(2) (3.3.3)	10	30	30	10
3	잘린 5세포		t{3,3,3}	(3) (3.6.6)			(1) (3.3.3)	10	30	40	20
4	알 수 있는 5세포		rr{3,3}	(2) (3.4.3.4)		(2) (3.4.4)	(1) (3.3.3.3)	20	80	90	30
7	캔트런으로 된 5셀		tr{3,3}	(2) (4.6.6)		(1) (3.4.4)	(1) (3.6.6)	20	80	120	60
8	구획 5셀		t0,1,3{3,3,3}	(1) (3.6.6)	(2) (4.4.6)	(1) (3.4.4)	(1) (3.4.3.4)	30	120	150	60

[3,3,3] 균일한 폴리토페스

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수			요소 개수
				포스3-0 (10)	포스1-2 (20)	알트	세포	얼굴	가장자리	정점
5	*런치 5-셀		t0,3{3,3,3}	(2) (3.3.3)	(6) (3.4.4)		30	70	60	20
6	*빗겨진 5-셀 데카코론		2t{3,3}	(4) (3.6.6)			10	40	60	30
9	*절삭된 5-셀		t0,1,2,3{3,3,3}	(2) (4.6.6)	(2) (4.4.6)		30	150	240	120
	옴니스너브[16]		ht0,1,2,3{3,3}	(2) (3.3.3.3.3)	(2) (3.3.3.3)	(4) (3.3.3)	90	300	270	60

별표(*)로 표시된 3개의 균일한 4폴리탑 형태는 5세포의 어떤 원소에 해당하는 원소를 이중 원소에 해당하는 원소와 교환할 수 있기 때문에 더 높은 확장형 5각 대칭인 240, [3,3]을 갖는다.하나의 작은 인덱스 서브그룹[3,3,3],⁺ 순서 60, 또는 그 더블링[3,3],⁺ 순서 120이 있으며, 완전성을 위해 나열되지만 균일하지 않은 전지형 5-셀을 정의한다.

B가족₄

이 패밀리는 24×16=384:4!=24 순열, 각 축의 반사를 위한 2⁴=16 순열, 4!=^[7]24 순열의 6각 대칭 [4,3,3]을 가지고 있다.3개의 작은 인덱스 하위 그룹이 있으며, 처음 두 개의 인덱스 하위 그룹은 다른 패밀리에서도 동일한 4 폴리탑을 생성하며, [1⁺,4,3,3], [4,3,3],⁺ [4,3,3],⁺ 모두 192를 주문한다.

큐세랙트 자르기

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수					요소 개수
				포스3길 (8)	포스2길 (24)	양수1길 (32)	양수 0 (16)	세포	얼굴	가장자리	정점
10	테서랙트 또는 8셀		{4,3,3}	(4) (4.4.4)				8	24	32	16
11	수정시방사선		r{4,3,3}	(3) (3.4.3.4)			(2) (3.3.3)	24	88	96	32
13	잘린 테세락트		t{4,3,3}	(3) (3.8.8)			(1) (3.3.3)	24	88	128	64
14	캔터케이티드 테세락트		rr{4,3,3}	(1) (3.4.4.4)		(2) (3.4.4)	(1) (3.3.3.3)	56	248	288	96
15	런케인테서락트 (또한 16-셀을 런케이티드)		t0,3{4,3,3}	(1) (4.4.4)	(3) (4.4.4)	(3) (3.4.4)	(1) (3.3.3)	80	208	192	64
16	비트런티드 테세락트 (또한 16-셀 비트)		2t{4,3,3}	(2) (4.6.6)			(2) (3.6.6)	24	120	192	96
18	칸트룬칼로리테스락트		tr{4,3,3}	(2) (4.6.8)		(1) (3.4.4)	(1) (3.6.6)	56	248	384	192
19	런티런탈테서락트		t0,1,3{4,3,3}	(1) (3.8.8)	(2) (4.4.8)	(1) (3.4.4)	(1) (3.4.3.4)	80	368	480	192
21	옴니트룬탈테서락트 (또한 전지 16개)		t0,1,2,3{3,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.6)	(1) (4.6.6)	80	464	768	384

관련 반정밀, [1⁺,4,3,3] 균일한 4-폴리탑

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수					요소 개수
				포스3길 (8)	포스2길 (24)	양수1길 (32)	양수 0 (16)	알트	세포	얼굴	가장자리	정점
12	반정차 데미테세락트 셀		= h{4,3,3}={3,4}	(4) (3.3.3)				(4) (3.3.3)	16	32	24	8
[17]	캔틱테서락트 (또는 잘린 16-셀)		= h2{4,3,3}=t{4,3,3}	(4) (6.6.3)			(1) (3.3.3.3)		24	96	120	48
[11]	룬틱 큐세락트 (또는 수정 테세락트)		= h3{4,3,3}=r{4,3,3}	(3) (3.4.3.4)			(2) (3.3.3)		24	88	96	32
[16]	런시칸틱테서락트 (혹은 비트런닝된 큐브레이크)		= h2,3{4,3,3}=2t{4,3,3}	(2) (3.4.3.4)			(2) (3.6.6)		24	120	192	96
[11]	(정확한 큐빅)		= h1{4,3,3}=r{4,3,3}						24	88	96	32
[16]	(2중경사)		= h1,2{4,3,3}=2t{4,3,3}						24	120	192	96
[23]	(수정된 24 셀)		= h1,3{4,3,3}=rrr{3,3,4}						48	240	288	96
[24]	(24-셀 분쇄)		= h1,2,3{4,3,}=tr{3,3,4}						48	240	384	192

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수					요소 개수
				포스3길 (8)	포스2길 (24)	양수1길 (32)	양수 0 (16)	알트	세포	얼굴	가장자리	정점
통일형	전지 누브 테세락트[17] (혹은 전지 16-셀)		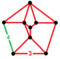ht0,1,2,3{4,3,3}	(1) (3.3.3.3.4)	(1) (3.3.3.4)	(1) (3.3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)	272	944	864	192

16셀 자르기

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수					요소 개수
				포스3길 (8)	포스2길 (24)	양수1길 (32)	양수 0 (16)	알트	세포	얼굴	가장자리	정점
[12]	16셀, 육각카초론[7]		{3,3,4}				(8) (3.3.3)		16	32	24	8
[22]	*수정된 16-셀 (24-셀과 동일)		= r{3,3,4}	(2) (3.3.3.3)			(4) (3.3.3.3)		24	96	96	24
17	잘린 16셀		t{3,3,4}	(1) (3.3.3.3)			(4) (3.6.6)		24	96	120	48
[23]	*알 수 있는 16세포 (수정된 24-셀과 동일)		= rr{3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.3.4)		48	240	288	96
[15]	룬케이트 16셀 (또한 런케이티드 8-셀)		t0,3{3,3,4}	(1) (4.4.4)	(3) (4.4.4)	(3) (3.4.4)	(1) (3.3.3)		80	208	192	64
[16]	박리 16셀 (또한 8-셀을 비트런으로 갈음)		2t{3,4}	(2) (4.6.6)			(2) (3.6.6)		24	120	192	96
[24]	*가공 16-셀 (자른 24-셀과 동일)		= tr{3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.6)		48	240	384	192
20	구획 16셀		t0,1,3{3,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.6)	(1) (3.6.6)		80	368	480	192
[21]	전지형 16셀 (또한 전지 8개)		t0,1,2,3{3,3,4}	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.6)	(1) (4.6.6)		80	464	768	384
[31]	교번식 캔트런 16 셀 (스너브 24-셀과 동일)		sr{3,4}	(1) (3.3.3.3.3)		(1) (3.3.3)	(2) (3.3.3.3.3)	(4) (3.3.3)	144	480	432	96
통일형	Runcic snub 정류 16-cell		sr3{3,4}	(1) (3.4.4.4)	(2) (3.4.4)	(1) (4.4.4)	(1) (3.3.3.3.3)	(2) (3.4.4)	176	656	672	192

(*) 사면체를 교정하면 팔면체가 생성되는 것과 마찬가지로 16세포를 교정하면 다음 계열의 정규 멤버인 24세포가 생성된다.

스너브 24셀은 완벽함을 위해 이 패밀리에 반복된다.칸티트런 16셀 또는 24셀을 번갈아 가며, 반대칭군[(3,⁺3,4]]을 가지고 있다.잘린 팔면세포는 이코사면체가 된다.정육면체는 4면체(tetrahedra)가 되고, 제거된 정점과의 틈새에 96개의 새로운 4면체(tetrahedra)가 생성된다.

F가족₄

이 계열은 24개 셀 각각에 대해 8면체의 48 대칭인 ^[7]24×48=1152 순서의 [3,4,3]의 dploid icositetrachoric 대칭을 가지고 있다.3개의 작은 인덱스 하위 그룹이 있으며, 처음 두 쌍의 이형성 쌍이 균일한 4-폴리탑을 생성하며, 다른 패밀리에서도 반복된다. [3,4,3], [3,3⁺⁺], [3,4,3],⁺ 모두 순서 576이다.

[3,4,3] 균일한 4개 항목

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수				요소 개수
				포스3길 (24)	포스2길 (96)	양수1길 (96)	양수 0 (24)	세포	얼굴	가장자리	정점
22	24셀, 이코시테트라초론[7] (수정된 16-셀과 동일)		{3,4,3}	(6) (3.3.3.3)				24	96	96	24
23	정류 24세포 (16-셀과 동일)		r{3,4,3}	(3) (3.4.3.4)			(2) (4.4.4)	48	240	288	96
24	잘린 24셀 (칸트런 16-셀과 동일)		t{3,4,3}	(3) (4.6.6)			(1) (4.4.4)	48	240	384	192
25	24세포로 알 수 있는		rr{3,4,3}	(2) (3.4.4.4)		(2) (3.4.4)	(1) (3.4.3.4)	144	720	864	288
28	캔트런 24셀		tr{3,4,3}	(2) (4.6.8)		(1) (3.4.4)	(1) (3.8.8)	144	720	1152	576
29	24구경.		t0,1,3{3,4,3}	(1) (4.6.6)	(2) (4.4.6)	(1) (3.4.4)	(1) (3.4.4.4)	240	1104	1440	576

[3⁺,4,3] 균일한 4개 항목

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수					요소 개수
				포스3길 (24)	포스2길 (96)	양수1길 (96)	양수 0 (24)	알트	세포	얼굴	가장자리	정점
31	†스너브 24세포		s{3,4,3}	(3) (3.3.3.3.3)			(1) (3.3.3)	(4) (3.3.3)	144	480	432	96
통일형	런치 스너브 24셀		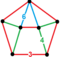s3{3,4,3}	(1) (3.3.3.3.3)	(2) (3.4.4)		(1) (3.6.6)	(3) 트리캅	240	960	1008	288
[25]	24세포의 통조림 (24-셀과 동일)		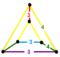s2{3,4,3}	(2) (3.4.4.4)			(1) (3.4.3.4)	(2) (3.4.4)	144	720	864	288
[29]	24셀의 대서양 스너브. (런시트가 24-셀과 동일)		s2,3{3,4,3}	(1) (4.6.6)		(1) (3.4.4)	(1) (3.4.4.4)	(2) (4.4.6)	240	1104	1440	576

(iii) 이곳의 스너브 24 셀은 일반적인 이름에도 불구하고 스너브 큐브와 유사하지 않으며, 오히려 잘린 24 셀의 교대로 인해 파생된다.그것의 대칭 수는 576에 불과하다. (이온 감소 이코시테트라코리아 그룹, [3⁺,4,3])

5세포와 마찬가지로 24세포는 자가이중이며, 따라서 다음의 3가지 형태는 대칭이 2배 많아 총량이 2304(확장 이코시테트라크리스틱 대칭 [3,4,3])에 이른다.

[3,4,3] 균일한 4각형 상단

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수		요소 개수
				포스3-0 (48)	포스2-1 (192)	세포	얼굴	가장자리	정점
26	윤택 24셀		t0,3{3,4,3}	(2) (3.3.3.3)	(6) (3.4.4)	240	672	576	144
27	24구경. 4등분자		2t{3,4,3}	(4) (3.8.8)		48	336	576	288
30	전지 24셀		t0,1,2,3{3,4,3}	(2) (4.6.8)	(2) (4.4.6)	240	1392	2304	1152

[3,4,3]⁺ 등각 4각형

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수			요소 개수
				포스3-0 (48)	포스2-1 (192)	알트	세포	얼굴	가장자리	정점
통일형	전지 24 셀[18]		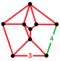ht0,1,2,3{3,4,3}	(2) (3.3.3.3.4)	(2) (3.3.3.3)	(4) (3.3.3)	816	2832	2592	576

H가족₄

이 계열은 120×120=24×600=14400: 120 도데카헤드라 각각에 대해 120, 600 사데카헤드라 각에 대해 24, 즉 6각 대칭[^[7]5,3,3]을 가진다.작은 인덱스 서브그룹 하나[5,3,3]가 있는데,⁺ 모두 7200을 주문한다.

120셀 절단

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	위치별 셀 수					요소 개수
				포스3길 (120)	포스2길 (720)	양수1길 (1200)	양수 0 (600)	알트	세포	얼굴	가장자리	정점
32	120 셀 (헤카토노사초론 또는 도데카콘타초론)[7]		{5,3,3}	(4) (5.5.5)					120	720	1200	600
33	정류된 120 셀		r{5,3,3}	(3) (3.5.3.5)			(2) (3.3.3)		720	3120	3600	1200
36	잘린 120셀		t{5,3,3}	(3) (3.10.10)			(1) (3.3.3)		720	3120	4800	2400
37	알 수 있는 120 셀		rr{5,3,3}	(1) (3.4.5.4)		(2) (3.4.4)	(1) (3.3.3.3)		1920	9120	10800	3600
38	재질의 120셀 (또한 600-셀을 런케이티드)		t0,3{5,3,3}	(1) (5.5.5)	(3) (4.4.5)	(3) (3.4.4)	(1) (3.3.3)		2640	7440	7200	2400
39	120셀의 박리. (또한 600-셀 비트코인)		2t{5,3,3}	(2) (5.6.6)			(2) (3.6.6)		720	4320	7200	3600
42	120셀의 캔트런을 가진		tr{5,3,3}	(2) (4.6.10)		(1) (3.4.4)	(1) (3.6.6)		1920	9120	14400	7200
43	120셀의 경사로를 달리다.		t0,1,3{5,3,3}	(1) (3.10.10)	(2) (4.4.10)	(1) (3.4.4)	(1) (3.4.3.4)		2640	13440	18000	7200
46	다량의 120셀 (또한 600셀의 전분포함)		t0,1,2,3{5,3,3}	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.6)	(1) (4.6.6)		2640	17040	28800	14400
통일형	전지 120 셀[19] (전미스너브 600셀과 동일)		ht0,1,2,3{5,3,3}	(1) (3.3.3.3.5)	(1) (3.3.3.5)	(1) (3.3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)	9840	35040	32400	7200

600셀 절단

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	대칭	위치별 셀 수				요소 개수
					포스3길 (120)	포스2길 (720)	양수1길 (1200)	양수 0 (600)	세포	얼굴	가장자리	정점
35	600셀, 육각시초론[7]		{3,3,5}	[5,3,3] 14400을 주문하다				(20) (3.3.3)	600	1200	720	120
[47]	20-1996 600 셀 (대항심)		논위토피안 건설	[[10,2+,10]] 400개를 주문하다 지수 36	(2) (3.3.3.5)			(12) (3.3.3)	320	720	500	100
[31]	24시간 6백 셀 (스너브 24-셀)		논위토피안 건설	[3+,4,3] 576호를 주문하다 지수 25	(3) (3.3.3.3.3)			(5) (3.3.3)	144	480	432	96
통일형	bi-24-1600-600 셀		논위토피안 건설	주문번호 144 지수 100	(6) tdi				48	192	216	72
34	정류 600셀		r{3,3,5}	[5,3,3]	(2) (3.3.3.3.3)			(5) (3.3.3.3)	720	3600	3600	720
통일형	120회 교정 600셀		논위토피안 건설	1200을 주문하다 색인 12	(2) 3.3.3.5	(2) 4.4.5		(5) P4	840	2640	2400	600
41	잘린 600셀		t{3,3,5}	[5,3,3]	(1) (3.3.3.3.3)			(5) (3.6.6)	720	3600	4320	1440
40	알 수 있는 600셀		rr{3,5}	[5,3,3]	(1) (3.5.3.5)	(2) (4.4.5)		(1) (3.4.3.4)	1440	8640	10800	3600
[38]	윤활유 600셀 (또한 120-셀을 달았다)		t0,3{3,3,5}	[5,3,3]	(1) (5.5.5)	(3) (4.4.5)	(3) (3.4.4)	(1) (3.3.3)	2640	7440	7200	2400
[39]	600셀의 박리. (또한 120-셀을 중첩)		2t{3,5}	[5,3,3]	(2) (5.6.6)			(2) (3.6.6)	720	4320	7200	3600
45	캔트런 600셀		tr{3,5}	[5,3,3]	(1) (5.6.6)	(1) (4.4.5)		(2) (4.6.6)	1440	8640	14400	7200
44	6백 셀을 달리다.		t0,1,3{3,3,5}	[5,3,3]	(1) (3.4.5.4)	(1) (4.4.5)	(2) (4.4.6)	(1) (3.6.6)	2640	13440	18000	7200
[46]	다량의 600셀 (또한 120 셀의 전분포함)		t0,1,2,3{3,3,5}	[5,3,3]	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.6)	(1) (4.6.6)	2640	17040	28800	14400

D가족₄

이 demiterstact 계열[3^1,1,1]은 새로운 통일된 4폴리탑을 도입하지 않지만, 이러한 대체 구조를 반복할 가치가 있다.이 패밀리는 4축의 순열 12×16=192:4!/2=12의 순열을 가지며, 절반은 교대로, 2⁴=16은 각 축의 반사로 한다.동일한 4-폴리토페[3]⁺를^1,1,1 생성하는 작은 인덱스 하위 그룹 하나가 있으며, 순서는 96이다.

[3^1,1,1] 균일한 4각형 상단

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 = =	위치별 셀 수					요소 개수
				양수 0 (8)	포스2길 (24)	양수1길 (8)	포스3길 (8)	포지. 알트 (96)	3	2	1	0
[12]	반신반의하다 반정도의 (16-셀과 동일)		= h{4,3,3}			(4) (3.3.3)	(4) (3.3.3)		16	32	24	8
[17]	통조림 테세락트 (잘린 16-셀과 동일)		= h2{4,3,3}	(1) (3.3.3.3)		(2) (3.6.6)	(2) (3.6.6)		24	96	120	48
[11]	런치 큐세락트 (수정된 큐빅과 동일)		= h3{4,3,3}	(1) (3.3.3)		(1) (3.3.3)	(3) (3.4.3.4)		24	88	96	32
[16]	대서양 테서락트 (비트런드 테세락트와 동일)		= h2,3{4,3,3}	(1) (3.6.6)		(1) (3.6.6)	(2) (4.6.6)		24	96	96	24

두 갈래로 갈라진 3개의 가지 노드가 동일한 링으로 울리면 [3[3^1,1,1] = [3,4,3]처럼 대칭이 6만큼 증가될 수 있으며, 따라서 이러한 폴리토페스는 24세포 계열에서 반복된다.

[3[3^1,1,1] 균일한 4각형 테두리

#	이름	꼭지점 형상을 나타내다	콕시터 다이어그램 = =	위치별 셀 수			요소 개수
				포지션 0,1,3 (24)	포스2길 (24)	포지. 알트 (96)	3	2	1	0
[22]	교정된 16세포 (24-셀과 동일)		= = = {31,1,1} = r{3,3,4} = {3,4,3}	(6) (3.3.3.3)			48	240	288	96
[23]	알 수 있는 16세포 (수정된 24-셀과 동일)		= = = r{31,1,1} = rr{3,4} = r{3,4,3}	(3) (3.4.3.4)	(2) (4.4.4)		24	120	192	96
[24]	캔트런으로 된 16셀 (자른 24-셀과 동일)		= = = t{31,1,1} = tr{3,3,4} = t{3,4,3}	(3) (4.6.6)	(1) (4.4.4)		48	240	384	192
[31]	24셀을 훔치다		= = = s{31,1,1} = sr{3,3,4} = s{3,4,3}	(3) (3.3.3.3.3)	(1) (3.3.3)	(4) (3.3.3)	144	480	432	96

여기서 다시 대칭 그룹[3^1,1,1]⁺을 가진 스너브 24 셀은 잘린 24 셀의 번갈아 잘라낸 부분을 나타내며, 삭제된 정점의 위치에 96개의 새로운 4차 테트라헤드를 생성한다.부분 스너브드 4 폴리토프로서 이전의 그룹 내에서 그것의 외관과 대조적으로, 이 대칭 그룹 내에서만 그것은 스너브 큐브와 스너브 도데체론 같은 케플러 스너브와 완전한 유추를 한다.

대반민주의

대항정신병이라고 알려진 비위토프 제복 볼록 4폴리토프는 300개의 사면체(Tetrahedra)로 연결된 2개의 수직 고리를 이루는 20개의 오각형 항정신병(Opthal Antiquar)으로 구성되어 있다.그것은 삼각형 띠로 연결된 두 개의 평행 다각형으로 이루어진 3차원 항정신병과는 느슨하게 유사하다.그러나 그들과는 달리 대항쟁은 일률적인 폴리토페스의 무한 계열의 일원이 아니다.

그것의 대칭은 이온 감소된 Coxeter 그룹, [10⁺,2,10], 순서 400이다.

#	이름	사진	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	유형별 셀		요소 개수				그물
							세포	얼굴	가장자리	정점
47	대반민주의			기호 없음	300 (3.3.3)	20 (3.3.3.5)	320	20 {5} 700 {3}	500	100

프리즘 균일 4폴리토프

프리즘 폴리토프는 낮은 차원의 두 개의 폴리토페로 이루어진 카르테시안 제품이다. 익숙한 예는 폴리곤과 선 세그먼트의 제품인 3차원 프리즘이다.프리즘 제복 4폴리탑은 두 개의 무한가족으로 구성된다.

• 다면 프리즘: 선 부분과 균일한 다면체의 산물.이 가문은 3차원 프리즘과 반격으로 만들어진 프리즘을 포함하고 있기 때문에 무한하다.
• 듀오프라임: 두 개의 폴리곤의 제품.

볼록 다면 프리즘

프리즘 4폴리토페스의 가장 분명한 계열은 다면 프리즘, 즉 선분할이 있는 다면체의 제품이다.그러한 4-폴리탑의 세포는 평행 하이퍼플레인(기본 셀)에 놓여 있는 두 개의 동일한 균일한 다면체와 그것들과 결합하는 프리즘 층(측면 셀)이다.이 패밀리는 75개의 비프리즘적 균일 다면체(이 중 18개는 볼록한 것이고, 그 중 하나인 큐브프리즘은 위에 큐브프랙트로 나열되어 있다)^{[citation needed]}에 대한 프리즘을 포함한다.

5개의 플라토닉 고형분과 13개의 아르키메데스 고형분뿐만 아니라 3차원 프리즘과 반격의 무한가족을 위해 만들어진 18개의 볼록 다면체 프리즘이 있다.^{[citation needed]}다면 프리즘의 대칭 번호는 기본 다면체의 2배이다.

사면체 프리즘:A₃ × A₁

이 프리즘적 사면 대칭은 [3,3,2] 순서 48이다.지수 2 부분군[(3,3)]⁺과 [3,3,2]⁺이 있지만, 두 번째 부분군은 균일한 4 폴리토프를 생성하지 않는다.

[3,3,2] 균일한 4개 항목

#	이름	사진	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	유형별 셀			요소 개수				그물
								세포	얼굴	가장자리	정점
48	사면 프리즘			{3,3}×{ } t0,3{3,3,2}	2 3.3.3	4 3.4.4		6	8 {3} 6 {4}	16	8
49	잘린 사면 프리즘			t{3,3}×{ } t0,1,3{3,3,2}	2 3.6.6	4 3.4.4	4 4.4.6	10	8 {3} 18 {4} 8 {6}	48	24

[[3,3],2] 균일한 4개 항목

#	이름	사진	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	유형별 셀			요소 개수				그물
								세포	얼굴	가장자리	정점
[51]	수정 사면 프리즘 (팔면 프리즘과 동일)			r{3,3}×{ } t1,3{3,3,2}	2 3.3.3.3	4 3.4.4		6	16 {3} 12 {4}	30	12
[50]	사면 프리즘(Cantellated 4면 프리즘 (동일한 큐옥타헤드랄 프리즘)			rr{3,3}×{ } t0,2,3{3,3,2}	2 3.4.3.4	8 3.4.4	6 4.4.4	16	16 {3} 36 {4}	60	24
[54]	칸티트룬 사면 프리즘 (잘린 팔면 프리즘과 동일)			tr{3,3}×{ } t0,1,2,3{3,3,2}	2 4.6.6	8 6.4.4	6 4.4.4	16	48 {4} 16 {6}	96	48
[59]	스너브 사면 프리즘 (이코사이드 프리즘과 동일)			sr{3,3}×{ }	2 3.3.3.3.3	20 3.4.4		22	40 {3} 30 {4}	72	24
통일형	전치사면 항정신병			${\displaystyle s\left\{\put\{\read}{l}3\3\\2\end{array}\right\}}}}$	2 3.3.3.3.3	8 3.3.3.3	6+24 3.3.3	40	16+96 {3}	96	24

팔면체₃ 프리즘: B × A₁

이 프리즘적 팔면체 가족 대칭은 [4,3,2, 순서 96]이다.지수 2, 순서 48의 6개의 하위 그룹이 있으며, 이 하위 그룹은 아래 4-폴리 토픽으로 번갈아 표현된다.대칭은 [(4,3),⁺2], [1,4⁺,3,2], [4,3⁺,2], [4,3⁺,2], [4,3,⁺2], [4,3,2]⁺이다.

#	이름	사진	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	유형별 셀				요소 개수				그물
									세포	얼굴	가장자리	정점
[10]	입방 프리즘 (테서랙트와 동일) (4-4 듀오프라시즘과 동일)			{4,3}×{ } t0,3{4,3,2}	2 4.4.4	6 4.4.4			8	24 {4}	32	16
50	큐폭타헤드랄 프리즘 (사면 프리즘과 동일)			r{4,3}×{ } t1,3{4,3,2}	2 3.4.3.4	8 3.4.4	6 4.4.4		16	16 {3} 36 {4}	60	24
51	팔면 프리즘 (수정된 사면 프리즘과 동일) (삼각형 항정신병 프리즘과 동일)			{3,4}×{ } t2,3{4,3,2}	2 3.3.3.3	8 3.4.4			10	16 {3} 12 {4}	30	12
52	롬비큐보톡타헤드랄 프리즘			rr{4,3}×{ } t0,2,3{4,3,2}	2 3.4.4.4	8 3.4.4	18 4.4.4		28	16 {3} 84 {4}	120	48
53	잘린 입방 프리즘			t{4,3}×{ } t0,1,3{4,3,2}	2 3.8.8	8 3.4.4	6 4.4.8		16	16 {3} 36 {4} 12 {8}	96	48
54	잘린 팔면 프리즘 (칸티트룬 사면 프리즘과 동일)			t{3,4}×{ } t1,2,3{4,3,2}	2 4.6.6	6 4.4.4	8 4.4.6		16	48 {4} 16 {6}	96	48
55	잘린 큐옥타헤드랄 프리즘			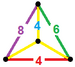tr{4,3}×{ } t0,1,2,3{4,3,2}	2 4.6.8	12 4.4.4	8 4.4.6	6 4.4.8	28	96 {4} 16 {6} 12 {8}	192	96
56	스너브 입방 프리즘		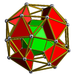	sr{4,3}×{ }	2 3.3.3.3.4	32 3.4.4	6 4.4.4		40	64 {3} 72 {4}	144	48
[48]	사면 프리즘			h{4,3}×{ }	2 3.3.3	4 3.4.4			6	8 {3} 6 {4}	16	8
[49]	잘린 사면 프리즘			h2{4,3}×{ }	2 3.3.6	4 3.4.4	4 4.4.6		6	8 {3} 6 {4}	16	8
[50]	큐폭타헤드랄 프리즘			rr{3,3}×{ }	2 3.4.3.4	8 3.4.4	6 4.4.4		16	16 {3} 36 {4}	60	24
[52]	롬비큐보톡타헤드랄 프리즘			s2{3,4}×{ }	2 3.4.4.4	8 3.4.4	18 4.4.4		28	16 {3} 84 {4}	120	48
[54]	잘린 팔면 프리즘			tr{3,3}×{ }	2 4.6.6	6 4.4.4	8 4.4.6		16	48 {4} 16 {6}	96	48
[59]	이코사헤드랄 프리즘			s{3,4}×{ }	2 3.3.3.3.3	20 3.4.4			22	40 {3} 30 {4}	72	24
[12]	16 셀		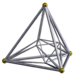	s{2,4,3}	2+6+8 3.3.3.3				16	32 {3}	24	8
통일형	전미뇌사면항정신병증			sr{2,3,4}	2 3.3.3.3.3	8 3.3.3.3	6+24 3.3.3		40	16+96 {3}	96	24
통일형	옴니스누브 큐빅 항정신병			${\displaystyle s\left\{\put\{\read}{l}4\\3\\2\end{array}\right\}}}}$	2 3.3.3.3.4	12+48 3.3.3	8 3.3.3.3	6 3.3.3.4	76	16+192 {3} 12 {4}	192	48
통일형	룬시크 스너브 큐빅 호소콘			s3{2,4,3}	2 3.6.6	6 3.3.3	8 삼각 큐폴라		16	52	60	24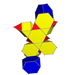

이코사이드 프리즘:H₃ × A₁

이 프리즘적 이두상 대칭은 [5,3,2, 순서 240]이다.지수 2 부분군[(5,3],⁺ 2], [5,3,2]⁺이 있지만, 두 번째 부분군은 균일한 폴리초론을 생성하지 않는다.

#	이름	사진	꼭지점 형상을 나타내다	콕시터 다이어그램 그리고 슐레플리 기호	유형별 셀				요소 개수				그물
									세포	얼굴	가장자리	정점
57	도데카헤드랄 프리즘			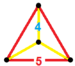{5,3}×{ } t0,3{5,3,2}	2 5.5.5	12 4.4.5			14	30 {4} 24 {5}	80	40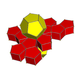
58	이코시다데카헤드랄 프리즘		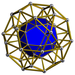	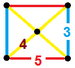r{5,3}×{ } t1,3{5,3,2}	2 3.5.3.5	20 3.4.4	12 4.4.5		34	40 {3} 60 {4} 24 {5}	150	60
59	이코사헤드랄 프리즘 (snub 사면 프리즘으로 표시됨)			{3,5}×{ } t2,3{5,3,2}	2 3.3.3.3.3	20 3.4.4			22	40 {3} 30 {4}	72	24
60	잘린두면 프리즘		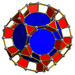	t{5,3}×{ } t0,1,3{5,3,2}	2 3.10.10	20 3.4.4	12 4.4.10		34	40 {3} 90 {4} 24 {10}	240	120
61	롬비코시도데코헤드랄 프리즘			rr{5,3}×{ } t0,2,3{5,3,2}	2 3.4.5.4	20 3.4.4	30 4.4.4	12 4.4.5	64	40 {3} 180 {4} 24 {5}	300	120
62	잘린 이두면 프리즘			t{3,5}×{ } t1,2,3{5,3,2}	2 5.6.6	12 4.4.5	20 4.4.6		34	90 {4} 24 {5} 40 {6}	240	120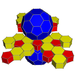
63	잘린 이코시다데카헤드랄 프리즘		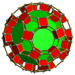	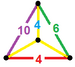tr{5,3}×{ } t0,1,2,3{5,3,2}	2 4.6.10	30 4.4.4	20 4.4.6	12 4.4.10	64	240 {4} 40 {6} 24 {10}	480	240
64	스너브 도데카프리즘 프리즘			sr{5,3}×{ }	2 3.3.3.3.5	80 3.4.4	12 4.4.5		94	160 {3} 150 {4} 24 {5}	360	120
통일형	오미스누브 도데카헤드랄 항정신병증			${\displaystyle s\left\{\put\{\put{array}{l}5\\\3\\2\end{array}\right\}}}}}$	2 3.3.3.3.5	30+120 3.3.3	20 3.3.3.3	12 3.3.3.5	184	20+240 {3} 24 {5}	220	120

듀오프라임: [p] × [q]

두 번째는 두 개의 일반 다각형의 산물인 통일된 두 개의 무한 계열이다.듀오프리즘의 콕시터-딘킨 도표는 입니다.그것의 꼭지점 모양은 분산형 사면체 입니다.

이 가족은 첫 번째와 겹친다: 두 "인자" 다각형 중 하나가 사각형일 때, 그 제품은 3차원 프리즘인 초프리즘에 해당한다.p-곤과 q-곤("p,q-duoprism")인 듀오프라즘의 대칭 번호는 p-gon이면 4pq이고, 요인이 둘 다 p-곤이면 대칭 번호는 8p이다².4.4이중주의라고도 할 수 있다.

p,q-duoprism(p ≥ 3, q q 3)의 요소는 다음과 같다.

• 세포: p-gonal 프리즘, q-gonal 프리즘
• 면: pq 사각형, p q-곤, q-곤
• 모서리: 2pq
• 정점: pq

3차원 반격의 무한 계열에 4차원의 균일한 아날로그가 존재하지 않는다.

p-q 듀오프라즘의 무한 집합 - p-gonal 프리즘, q-gonal 프리즘:

이름	콕시터 그래프	세포	이미지들	그물
3-3 듀오프리즘		3+3 삼각 프리즘
3-4 듀오프리즘		큐브 3개 삼각형 프리즘 4개
4-4 듀오프리즘 (테서락트처럼)		4+4 큐브
3-5 듀오프리즘		오각형 프리즘 3개 삼각 프리즘 5개
4-5 듀오프리즘		오각형 프리즘 4개 정육면체 5개
5-5 듀오프리즘		5+5 오각형 프리즘
3-6 듀오프리즘		육각 프리즘 3개 6 삼각 프리즘
4-6 듀오프리즘		육각 프리즘 4개 6입방체
5-6 듀오프리즘		육각 프리즘 5개 오각형 프리즘 6개
6-6 듀오프리즘		6+6 육각 프리즘

3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

다각형 프리즘: [p] × [ ] × ]

균일한 프리즘 프리즘의 무한 집합은 4-p 듀오프라임과 겹친다: (p≥3) - p큐브와 4-gonal 프리즘 - (모두 4-p 듀오프라즘과 같다)시리즈 중 두 번째 폴리토프는 일반 테세락트 {4}×{4}의 낮은 대칭이다.

볼록 p-곤 프리즘

이름	{3}×{4}	{4}×{4}	{5}×{4}	{6}×{4}	{7}×{4}	{8}×{4}	{p}×{4}
콕시터 도표
이미지
세포	3 {4}×{} 4 {3}×{}	4 {4}×{} 4 {4}×{}	5 {4}×{} 4 {5}×{}	6 {4}×{} 4 {6}×{}	7 {4}×{} 4 {7}×{}	8 {4}×{} 4 {8}×{}	p {4}×{} 4 {p}×{}
그물

다각형 항균 프리즘: [p] × [ ] × [ ] ]

균일 항정신병 프리즘의 무한 집합은 (p≥2) - 2 p-곤 항정신병 2개와 삼각 프리즘 2개로 연결된 2개의 평행 균일 항정신병에서 구성된다.

볼록 p-곤 항균 프리즘

이름	s{2,2}×{}	s{2,3}×{}	s{2,4}×{}	s{2,5}×{}	s{2,6}×{}	s{2,7}×{}	s{2,8}×{}	s{2,p}×{}
콕시터 도표를 만들다
이미지
꼭지점 형상을 나타내다
세포	2초{2,2} (2) {2}×{}={4} 4 {3}×{}	2초{2,3} 2 {3}×{} 6 {3}×{}	2초{2,4} 2 {4}×{} 8 {3}×{}	2초{2,5} 2 {5}×{} 10 {3}×{}	2초{2,6} 2 {6}×{} 12 {3}×{}	2초{2,7} 2 {7}×{} 14 {3}×{}	2초{2,8} 2 {8}×{} 16 {3}×{}	2초{2,p} 2 {p}×{} 2p {3}×{}
그물

p-곤 항정신병 프리즘은 4p 삼각형, 4p 사각형, 4p-곤 면을 가지고 있다.그것은 가장자리가 10p, 꼭지점이 4p이다.

불균형 교대

콕시터는 모든 링이 교대로 표시된 4위 콕시터 그룹에 대해 2개의 균일한 솔루션만 선보였다(빈 원 노드로 표시).첫 번째는 , s{2^1,1,1}로서, demitesseract의 지수 24 부분군(대칭 [2,2,2],⁺ 순서 8) 형태, , h{4,3,3} (대칭 [1⁺,4,3] = [3^1,1,1], 순서 192)를 나타낸다.두 번째는 , s{3^1,1,1}이며, 이는 인덱스 6 서브그룹(대칭 [3^1,1,1],⁺ 순서 96) 형태의 스너브 24 셀, , , s{3,4,3}(대칭 [3⁺,3,3, 순서 576])이다.

전체적으로 동일한 에지 길이에 대한 해결이 지나치게 결정되므로 (6개의 방정식이 있지만 4개의 변수만 있는) , 같은 다른 대체는 균일하게 만들 수 없다.이러한 균일하지 않은 대체 도형은 전체 링 도형의 정점 두 개 중 하나를 제거하여 정점 변환 4 폴리 상단으로 구성할 수 있지만 가장자리 길이가 동일하지 않다.획일적인 교대조처럼, 그들은 [4,3,3],⁺ 순서 192와 같이 획일적인 인물의 대칭의 절반을 가질 것이다.^[20]

교대체가 있는 와이토프 구조는 정점 변환 수치를 만들어 내지만, 정점이 제거된 정점 주위의 교대된 간격은 정규 또는 반정맥이 아닌 셀을 생성하기 때문에 균일하지 않다.그러한 인물들의 제안된 이름은 메스폼 다항상이다.^[21]이 범주는 예를 들어 삼각 큐폴라와 같은 존슨 고형분의 일부를 세포로 허용한다.

존슨 솔리드 내의 각 꼭지점 구성은 꼭지점 수치 내에 존재해야 한다.예를 들어 사각형 프라미드는 베이스 둘레 3.3.4와 정점에 3.3.3.3의 두 꼭지점 구성을 가지고 있다.

두 볼록한 경우의 그물과 꼭지점 그림은 각 꼭지점 주변의 세포 목록과 함께 아래에 제시되어 있다.

균일하지 않은 세포가 있는 대류 꼭지점 4-폴리톱 2개

콕시터 도표를 만들다	s3{2,4,3}	s3{3,4,3}
관계	의 48정점 중 24정점 롬비큐옥타헤드랄 프리즘	576 정점의 288 24구경.
그물	런치 스너브 큐빅 호소코론[22][23]	런치 스너브 24셀[24][25]
세포
꼭지점 형상을 나타내다	(1) 3.4.3.4: 삼각 큐폴라 (2) 3.4.6: 삼각 큐폴라 (1) 3.3.3: 사면체 (1) 3.6.6: 잘린 사면체	(1) 3.4.3.4: 삼각 큐폴라 (2) 3.4.6: 삼각 큐폴라 (2) 3.4.4: 삼각 프리즘 (1) 3.6.6: 잘린 사면체 (1) 3.3.3.3.3: 이코사헤드론

46개의 비프리스마틱 와이토피안 유니폼 폴리초라 기하학적 파생

46개의 Wythoffian 4폴리탑에는 6개의 볼록형 4폴리탑이 있다.나머지 40개는 대칭의 대부분 또는 전부를 보존하는 기하학적 연산에 의해 정규 다초라에서 파생될 수 있으며, 따라서 이들이 공통적으로 가지고 있는 대칭 그룹에 의해 분류될 수도 있다.

잘라내기 작업의 요약 차트

기본 영역에 있는 원반경 생성기 지점의 위치 예

일반 4폴리토프에서 40개의 균일한 4폴리토프를 도출하는 기하학적 연산은 절삭 연산을 하고 있다.4 폴리토프는 꼭지점, 가장자리 또는 면에서 잘려져 아래 표의 열에 표시된 것처럼 그러한 요소에 해당하는 셀이 추가될 수 있다.

Coxeter-Dynkin 도표는 Wythoffian Kaleidoscope의 4개의 거울을 노드로 표시하며, 노드 사이의 가장자리에는 미러 사이의 각도를 나타내는 정수( labeled/n radians 또는 180/n도)가 표시된다.원형 노드는 각 형태에 대해 활성 상태인 미러를 보여준다. 거울은 놓여 있지 않은 정점에 대해 활성화된다.

작전	슐레플리 기호	대칭	콕시터 다이어그램	설명
부모	t0{p,q,r}	[p,q,r]		원본 정규 양식 {p,q,r}
정류	t1{p,q,r}			원래 가장자리가 점으로 변질될 때까지 적용되는 잘라내기 작업.
양방향화 (수정된 이중)	t2{p,q,r}			얼굴이 포인트까지 완전히 잘렸다.수리된 듀얼과 동일함.
삼보정 (iii)	t3{p,q,r}			세포가 점으로 잘려 있다.일반 이중 {r,q,p}
잘림	t0,1{p,q,r}			각 정점은 원래 가장자리의 중간 부분이 남아 있도록 잘려져 있다.꼭지점이 있던 곳에는 부모의 꼭지점 모양인 새로운 세포가 나타난다.각각의 원래의 세포도 마찬가지로 잘려 있다.
비트런지화	t1,2{p,q,r}			수정한 양식과 이중 수정한 양식 사이의 잘림.
삼중수소화	t2,3{p,q,r}			잘린 이중 {r,q,p}.
창법	t0,2{p,q,r}			가장자리와 정점에 적용되는 잘림이며 정규 및 이중 수정 양식 사이의 진행을 정의한다.
바이칸텔레이션	t1,3{p,q,r}			표시식 이중 {r,q,p}.
런시네이션 (또는 확장)	t0,3{p,q,r}			셀, 면 및 가장자리에 적용되는 잘림; 정규 형태와 이중 형태 사이의 진행을 정의한다.
캔티런케이션	t0,1,2{p,q,r}			통조림과 잘림 작업이 함께 적용되었다.
바이칸티트런지케이션	t1,2,3{p,q,r}			Cantitruncold 이중 {r,q,p.
런시티케이션	t0,1,3{p,q,r}			런닝 작업과 잘림 작업이 함께 적용되었다.
런시칸텔레이션	t0,1,3{p,q,r}			런시트가 적용된 이중 {r,q,p}.
잡식성 (runcicantitruncation)	t0,1,2,3{p,q,r}			세 연산자 모두 적용.
절반	h{2p,3,q}	[1+,2p,3,q] =[ (3,p,3)),q]		의 교대, 와 동일
캔틱	h2{2p,3,q}			와 같다
룬치크	h3{2p,3,q}			와 같다
런시칸틱	h2,3{2p,3,q}			와 같다
쿼터	q{2p,3,2q}	[1+,2p,3,2q,1+]		와 같다
스너브	s{p,2q,r}	[p+,2q,r]		교번 절단
캔틱 스너브	s2{p,2q,r}			알 수 있는 교번 절단
룬스크 스너브	s3{p,2q,r}			런케이티드 대체 잘라내기
룬시칸틱 스너브	s2,3{p,2q,r}			런시컨텔링 교번 절단
스너브 수정	sr{p,q,2r}	[(p,q)+,2r]		교대로 잘린 정류
	ht0,3{2p,q,2r}	[(2p,q,2r,2+)]		대체 런캐인팅
비스눕	2s{2p,q,2r}	[2p,q+,2r]		대체 비트런지
옴니스누브	ht0,1,2,3{p,q,r}	[p,q,r]+		교대성성성

또한 볼록한 균일한 벌집형 벌집들을 참조하라. 이 중 일부는 일반적인 입방형 벌집형 벌집에 적용되는 이러한 작동을 보여준다.

만약 두 개의 폴리에스테르가 서로 이중인 경우(테서락트, 16셀, 또는 120셀, 600셀 등) 비트런팅, 런닝 또는 옴트런캐스팅은 다른 하나에 대해 동일한 연산과 동일한 형상을 생성한다.따라서 표에 분사만 나타나는 경우 어느 한쪽 부모에게나 적용되는 것으로 이해해야 한다.

A₄, B₄, F₄, H₄ 대칭으로 구성된 46개의 균일한 폴리초라는 완전한 확장 대칭도와 Coxeter 도표로 이 표에 제시되어 있다.교대는 치랄 대칭에 따라 분류된다.스너브 24-셀은 3개 계열의 구조물이지만 모든 교체가 주어진다.괄호 안의 카운트는 반복측정 또는 균일하지 않다.Coxeter 다이어그램은 첨자 지수 1부터 46까지 주어진다.3-3번과 4-4번 이중주교 가문이 포함되어 있는데, B가족과의₄ 관계에 대해서는 두 번째가 된다.

콕시터군	확장됨	폴리초라		치랄 연장된	교대집집집
[3,3,3]	[3,3,3] (주문 120)	6	(1) (2) (3) (4) (7) (8)
	[2+[3,3,3]] (240 주문)	3	(5) (6) (9)	[2+[3,3,3]]+ (주문 120)	(1)	(−)
[3,31,1]	[3,31,1] (192번 주문)	0	(iii)
	[1[3,31,1]]=[4,3,3] = (주문 384)	(4)	(12) (17) (11) (16)
	[3[31,1,1]]=[3,4,3] = (주문 1152)	(3)	(22) (23) (24)	[3[3,31,1]]+ =[3,4,3]+ (주문 576)	(1)	(31) (= ) (−)
[4,3,3]	[3[1+,4,3,3]]=[3,4,3] = (주문 1152)	(3)	(22) (23) (24)
	[4,3,3] (주문 384)	12	(10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21)	[1+,4,3,3]+ 96)	(2)	(12) (= ) (31) (−)
				[4,3,3]+ (192번 주문)	(1)	(−)
[3,4,3]	[3,4,3] (주문 1152)	6	(22) (23) (24) (25) (28) (29)	[2+[3+,4,3+]] (주문 576)	1	(31)
	[2+[3,4,3]] (2304 주문)	3	(26) (27) (30)	[2+[3,4,3]]+ (주문 1152)	(1)	(−)
[5,3,3]	[5,3,3] (14400 주문)	15	(32) (33) (34) (35) (36) (37) (38) (39) (40) (41) (42) (43) (44) (45) (46)	[5,3,3]+ (주문 7200)	(1)	(−)
[3,2,3]	[3,2,3] (주문 36)	0	(iii)	[3,2,3]+ (18번 주문)	0	(iii)
	[2+[3,2,3]] (주문 72)	0		[2+[3,2,3]]+ (주문 36)	0	(iii)
	[[3],2,3]=[6,2,3] = (주문 72)	1		[1[3,2,3]]=[[3],2,3]+=[6,2,3]+ (주문 36)	(1)
	[(2+,4)[3,2,3]]=[2+[6,2,6]] = (주문 288)	1		[(2+,4)[3,2,3]]+=[2+[6,2,6]]+ (144 주문)	(1)
[4,2,4]	[4,2,4] (64번 주문)	0	(iii)	[4,2,4]+ (주문 32)	0	(iii)
	[2+[4,2,4]] (128)	0	(iii)	[2+[(4,2+,4,2+)]] (64번 주문)	0	(iii)
	[(3,3)[4,2*,4]]=[4,3,3] = (주문 384)	(1)	(10)	[(3,3)[4,2*,4]]+=[4,3,3]+ (192번 주문)	(1)	(12)
	[[4],2,4]=[8,2,4] = (128)	(1)		[1[4,2,4]]=[[4],2,4]+=[8,2,4]+ (64번 주문)	(1)
	[(2+,4)[4,2,4]]=[2+[8,2,8]] = (512 주문)	(1)		[(2+,4)[4,2,4]]+=[2+[8,2,8]]+ (주문 256)	(1)

참고 항목

• 4공간의 유한정규 다면체
• 볼록한 균일 벌집 - 유클리드 3공간의 무한 4폴리탑.
• 쌍곡선 공간의 볼록한 균일 벌집 - 쌍곡선 3-공간의 무한 4-폴리톱.
• 파라콤팩트 균일 벌집

참조

• A. Boole Stott: 일반 폴리토페와 공간충전에서 반정형의 기하학적 차감, 코닌클리케 아카데미 판 웨텐샤펜 폭 단위 암스테르담, 에르스테 챕티 11,1, 암스테르담, 1910
• B. GrünbaumConvex Polytopes, New York; London : Springer, c2003.ISBN0-387-00424-6.
  Volker Kaibel, Victor Klee, Günter M. Ziegler가 준비한 2판.
• Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen, ISBN 1-4181-7968-X [3] [4]
• H.S.M. Coxeter:
  • H.S.M. Coxeter, M. Longuet-Higgins und J.C.P. Miller:1954년 런던 왕립학회의 철학적 거래, 통일 폴리헤드라
  • H.S.M. Coxeter, 일반 폴리토페스, 제3판 도버 뉴욕, 1973년
• 케일리디스코어: F가 편집한 H.S.M. Coxeter의 선별된 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6
  • (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380-407, MR 2,10]
  • (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559-591]
  • (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3-45]
• H.S.M. Coxeter와 W. O. J. Moser.이산 그룹용 생성기 및 관계 4번째 에드 스프링어-버래그.1980년 92년 122년 뉴욕
• 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라우스, 2008년 사물의 대칭성, ISBN 978-1-56881-220-5 (제26장)
• 존 H. 콘웨이와 M.J.T. 가이: 4차원 아르키메데스 폴리토페스, 코펜하겐에서의 볼록성에 관한 콜로키움의 진행, 1965년 38페이지/39페이지
• N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
• N.W. Johnson: 기하학과 변환, (2015) 11장: 유한대칭군
• 리처드 클라이칭, 스너브스, 대체 면과 스콧-콕시터-딘킨 도표, 대칭: 문화와 과학, 제21권, 제4권, 329-344권, (2010) [5]
• Schoute, Pieter Hendrik (1911), "Analytic treatment of the polytopes regularly derived from the regular polytopes", Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam, 11 (3): 87 pp 구글북, 370-381

외부 링크

• 볼록형 균일 4폴리톱
  • 4차원의 균일하고 볼록한 폴리탑, 마르코 뮐러(독일어)
  • 4차원의 균일한 폴리토페스, 조지 올셰프스키.
    1. 볼록한 제복 폴리초라 펜타코론, 조지 올셰프스키를 기반으로 한다.
    2. 테서락트/16-셀에 기초한 볼록스 균일 폴리초라, 조지 올셰프스키.
    3. 24-셀 George Olshevsky를 기반으로 한 볼록스 제복 폴리초라.
    4. 120 셀/600 셀, George Olshevsky에 기초한 볼록스 균일 폴리초라.
    5. 변칙적인 볼록한 제복 폴리초론: (대항정신병), 조지 올셰프스키.
    6. 볼록한 균일한 프리즘 폴리초라, 조지 올셰프스키.
    7. George Olshevsky, George Olshevsky에서 유래된 균일한 폴리초라.
  • 정규 및 반정규 볼록 폴리토프 짧은 역사 개요
  • 소스를 포함한 Java3D 애플릿
• 비콘벡스 균일 4폴리톱
  • 조나단 바우어스의 제복 폴리초라
  • 스텔라4D 스텔라(소프트웨어)는 64개의 볼록 형태와 무한 프리즘 계열 등 알려진 균일한 폴리초라의 인터랙티브 뷰를 제작한다.
• Klitzing, Richard. "4D uniform polytopes".
• 4D-Polytopes and Their Dual Polytopes of the Coxeter Group W(A4) Represented by Quaternions International Journal of Geometric Methods in Modern Physics,Vol. 9, No. 4 (2012) Mehmet Koca, Nazife Ozdes Koca, Mudhahir Al-Ajmi (2012) [6]

v t 치수 2-10의 기본 볼록형 일반 및 균일한 폴리토프
가족	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
정규 다각형	삼각형	사각형	p-곤	육각형	펜타곤
균일다면체	사면체	옥타헤드론 • 큐브	데미큐브		도데카헤드론 • 이코사헤드론
균일 폴리초론	펜타코론	16-셀 • 테세락트	데미테세락트	24셀	120 셀 • 600 셀
제복5폴리토프	5와섹스	5정형 • 5정형	5데미큐브
제복6폴리토프	6-630x	6-정통 • 6-118	6데미큐브	122 • 221
제복7폴리토프	7시 15분	7정맥 • 7정맥	7데미큐브	132 • 231 • 321
제복8폴리토프	8시 15분	8정형 • 8정형	8데미큐브	142 • 241 • 421
제복9폴리토프	9시 15분	9-정통 • 9-11	9데미큐브
균일 10폴리토프	10센트짜리	10정형 • 10정형	10데미큐브
균일 n폴리토프	n-제곱스	n-직관 • n-직관	n-데미큐브	1k2 • 2k1 • k21	n-자갈 폴리토프
주제: 폴리토페 패밀리 • 일반 폴리토페 • 일반 폴리토페 및 화합물 목록