자율 시스템(수학)

선형 자율 시스템 ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$= ${\displaystyle A}$ ${\displaystyle x}$, ${\displaystyle x'=Ax,}$의 Poincaré 지도를 특징에 따라 안정적이거나 불안정한 것으로$$ 분류하는 안정성 다이어그램. 안정성은 일반적으로 도표 왼쪽까지 증가한다.^[1] 어떤 싱크, 소스 또는 노드는 평형점이다.

2차원 케이스는 위상 평면을 가리킨다.

수학에서 자율방정식이나 자율방정식은 독립변수에 명시적으로 의존하지 않는 보통의 미분방정식의 체계다. 변수가 시간일 때는 시간 변광성 계통이라고도 한다.

일반적으로 독립변수를 시간이라고 가정하는 물리학의 많은 법칙은 현재 보유하고 있는 자연의 법칙이 과거나 미래의 어떤 지점에 대한 법칙과 동일하다고 가정되기 때문에 자율적인 시스템으로 표현된다.

자율 시스템은 역동적인 시스템과 밀접한 관련이 있다. 어떤 자율적인 시스템은 역동적인 시스템으로^{[citation needed]} 변환될 수 있고, 매우 약한 가정을^{[citation needed]} 통해 역동적인 시스템은 자율적인 시스템으로^{[citation needed]} 변환될 수 있다.

정의

자율방식은 형태의 일반적인 미분방정식의 체계다.

${\displaystyle {\frac {d}{dt}x(t)=f(x(t)}}$

여기서 x는 n차원 유클리드 공간에서 값을 취한다; t는 종종 시간으로 해석된다.

그것은 형태의 미분방정식과 구별된다.

${\displaystyle {\frac {d}{dt}x(t)=g(x(t),t)}$

시스템의 진화를 지배하는 법률이 시스템의 현재 상태에만 의존하는 것이 아니라 매개변수 t에도 의존하는 경우, 다시 종종 시간으로 해석된다; 그러한 시스템은 정의에 의해 자율적이지 않다.

특성.

솔루션은 수평 번역 시 불변함:

$x{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$( ${\displaystyle t}$) ${\displaystyle x_{1}(t)}$을(를) 자율 시스템의 초기 값 문제의 고유한 해결책이 되도록 하십시오$$.

${\dplaystyle {\frac {d}{dt}x(t)=f(x(t)\####x(0)=x_{0}.}$

그러면 $x{\displaystyle {}_{}}$ ${\displaystyle 2{}_{}}$( t${\displaystyle }$)${\displaystyle }$= x ${\displaystyle {1\mathrm{}}_{}}$( t${\displaystyle }$- ${\displaystyle {t\mathrm{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle x_{2}(t)=x_{1}(t-t_{0})$이 해결됨

${\dplaystyle {\frac {d}{dt}x(t)=f(x(t)\#####x(t_{0})=x_{0}.}$

${\displaystyle {실제로\mathrm{}}_{}}$ $s{\displaystyle }$ = t -${\displaystyle }$t ${\displaystyle {}_{}}$ ${\$${\displaystyle =}$t-t_{0}을$나타내는$x 1$$$($ $s{\displaystyle {}_{}}$)${\displaystyle }$= ${\displaystyle x}$ ${\displaystyle {2\mathrm{}}_{}}$ t ) $displaystyle x_{1}(s)=x_{2}(t)}$ 및$$ ${\displaystyle d}$= ${\displaystyle d}$ ${\displaystyds=dt}$이 있다$.$

${\dplaystyle {\frac {d}{dt}x_{2}(t)={\frac {d}{d}}{d}}x_{1}(t-t_{0})={\frac {d}}}{d}}}}x_{1}(s)=f(x_{2}(t)=f.}$

초기 조건의 경우 검증은 사소한 것이지만

${\displaystyle x_{2}(t_{0})=x_{1}(t_{0}-t_{0})=x_{0}.}$

예

${\displaystyle y}$ ${\displaystyle {\prime }^{}}$=${\displaystyle }$( ${\displaystyle 2}$- y${\displaystyle }$) y ${\displaystyle y'=\left(2-y\right)y}$ 방정식은 독립$$ 변수이므로 $x{\displaystyle }$ ${\displaystyle x$라고 부르자 등식에 명시적으로 나타나지 않는다. 이 방정식에 대한 기울기 필드 및 등사선을 표시하려면 GNU 옥타브/MATLAB에서 다음 코드를 사용하십시오.

푸눈 = @(X, Y)(2 - Y) .* Y; % 함수 f(x,y)=(2-y)y [X, Y] = 메쉬그리드(0:.2:6, -1:.2:3); % 플롯 크기 선택 DY = 푸눈(X, Y); DX = 하나(사이즈를 맞추다(DY)); % 플롯 값 생성 부들부들 떨다(X, Y, DX, DY, 'k'); % 검정색으로 방향 필드 그림 보유하다 에 관하여; 등고선(X, Y, DY, [0 1 2], 'g'); 녹색으로 등축선(0 1 2) 추가 비율 칭호를 붙이다('f(x,y)=(2-y)y의 기울기 필드 및 등각선') 

One can observe from the plot that the function ${\displaystyle \left(2-y\right)y}$ is ${\displaystyle x}$-invariant, and so is the shape of the solution, i.e. ${\displaystyle y(x)=y(x-x_{0})}$ for any shift ${\displaystyle x_{0}}$.

MATLAB에서 실행을 통해 기호적으로 방정식 해결

syms y(x); 방정식 = (산산이 흩어지다(y) == (2 - y) * y); %는 일반 용액의 방정식을 상징적으로 해결함 y_일반 = 덤블링하다(방정식); 

$y{\displaystyle }$ =${\displaystyle 0}$ ${\displaystyle$ y$=0}$ 및$$ y${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle y=2$ 그리고 알 수 없는 상수 $C{\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$을 포함하는 세 번째 솔루션을 구한다$.$ -2 / (exp(C3 - 2 * x) - 1).

초기 조건에 대한 특정 값을 선택하면 몇 가지 해결책의 그림을 추가할 수 있다.

등각선 및 솔루션이 있는 경사 필드

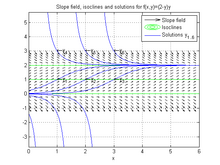
%는 초기 값 문제를 상징적으로 해결함 다른 초기 조건의 백분율 y1 = 덤블링하다(방정식, y(1) == 1); y2 = 덤블링하다(방정식, y(2) == 1); y3 = 덤블링하다(방정식, y(3) == 1); y4 = 덤블링하다(방정식, y(1) == 3); y5 = 덤블링하다(방정식, y(2) == 3); y6 = 덤블링하다(방정식, y(3) == 3); % 솔루션 플롯 이즈플롯(y1, [0 6]); 이즈플롯(y2, [0 6]); 이즈플롯(y3, [0 6]); 이즈플롯(y4, [0 6]); 이즈플롯(y5, [0 6]); 이즈플롯(y6, [0 6]); 칭호를 붙이다('f(x,y)=(2-y)y에 대한 기울기 필드, 등각선 및 솔루션') 전설('슬로프 필드', '등각선', '솔루션 y_{1..6}'); 문자 메시지를 보내다([1 2 3], [1 1 1], 발가벗기다('\왼쪽 화살표', {'y_1', 'y_2', 'y_3'})); 문자 메시지를 보내다([1 2 3], [3 3 3], 발가벗기다('\왼쪽 화살표', {'y_4', 'y_5', 'y_6'})); 격자무늬 에 관하여; 

정성분석

자율 시스템은 위상 공간을 사용하여 정성적으로 분석할 수 있다. 단변수의 경우 이것이 위상선이다.

솔루션 기법

1차원 자율 미분방정식에 적용되는 기법은 다음과 같다. $순서{\displaystyle }$ $n{\displaystyle }$ ${\displaystyle n}$의 모든 1차원 방정식은 n ${\displaystyle n}$ -차원$$ 1차적 시스템(일차적 시스템으로 축소하여 설명함)과 동일하지만$$, 반드시 그 반대의 경우도 아니다.

퍼스트 오더

1차 자율방정식

${\displaystyle {\frac {dx}{dt}=f(x)}$

분리할 수 있기 때문에, 그것을 본질적인 형태로 재배열하면 쉽게 해결될 수 있다.

${\displaystyle t+C=\int {\frac {dx}{f(x)}}}$

두 번째 순서

2차 자율방정식

${\displaystyle {\frac {d^{2}x}{dt^{2}}=f(x,x')}$

더 어렵지만 새로운 변수를 도입하면 해결할^[2] 수 있다.

${\displaystyle v={\frac {dx}{dt}}}$

그리고 체인 규칙을 통해$$ $x{\displaystyle }$ ${\displaystyle x}$의 두 번째 파생 모델을 다음과 같이 표현한다.

${\dplaystyle {\frac{d^{2}x}{dt^{2}}={\frac {dx}{dt}={\frac {dx}{dt}}{\frac}}}{dx}}}{\frac}=v{\frac}{dx}{dx}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

원래의 방정식이 될 수 있도록

${\displaystyle v{\frac {filename}{dx}=f(x,v)}$

$독립{\displaystyle }$ 변수 $t{\displaystyle }$ ${\displaystyle t}$에 대한 참조가 없는 첫 번째 순서 방정식$.$ v ${\displaystyle v}$을(를) $x{\displaystyle }$ ${\displaystyle x}$의 함수로 제공한다$.$ $그런{\displaystyle }$ 다음 v ${\displaystyle v}$의 정의를 호출하십시오$.$

${\dplaystyle {\frac {dx}{dt}=v(x)\quad \Rightarrow \quad t+C=\int {\frac {dx}{v(x)}}}}}}$

암묵적인 해결책이지

특수 케이스: x" = f(x)

$f{\displaystyle }$ ${\displaystyle f}$이(가) $x{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$ x$'}$과(와) 독립된 특수 사례

${\displaystyle {\frac {d^{2}x}{dt^{2}}=f(x)}$

별개의 치료의 ^[3]혜택 이러한 유형의 방정식은 항상 해밀턴식 계통이기 때문에 고전 역학에서 매우 흔하다.

그 아이디어는 그 정체성을 이용하는 것이다.

${\displaystyle {\frac {dx}{dt}}=\좌측값\frac {dt}{dx}\우측)^{-1}$

그것은 사슬 규칙에서 따르며, 0으로 나누어져서 생기는 어떤 이슈도 배제한다.

첫 번째 순서 자율 시스템의 양쪽을 뒤집음으로써 $x{\displaystyle }$ ${\displaystyle x}$에 대해 즉시 통합할 수 있다$.$

${\dplaystyle {\frac {dx}{dt}=f(x)\quad \Rightarrow \quad \quad {\frac {dt}{dx}}={dx}}={\frac \c(x)}}}$

변수 기법의 분리를 볼 수 있는 또 다른 방법이다. 고차 방정식으로 이런 걸 할 수 있을까? 답은 2차 방정식은 맞지만, 할 일이 더 많다. 두 번째 파생상품은 $t{\displaystyle }$ ${\displaystyle t}$이(가) 아닌 $x{\displaystyle }$ ${\displaystyle x}$에 대한 파생상품으로 표현되어야 한다$.$

${\displaystyle{\begin{정렬}{\frac{{2d^}x}{dt^{2}}}&={\frac{d}{dt}}\left({\frac{dx}{dt}}\right)={\frac{d}{dx}}\left({\frac{dx}{dt}}\right){\frac{dx}{dt}}\\[4pt]&, ={\frac{d}{dx}}\left(\left({\frac{dt}{dx}}\right)^{)}\right)\leftᆭ^ᆻ\\[4pt]&, =-\left({\frac{dt}{dx}}\right)^{-2}{\frac{{2d^}t}{dx^{2}}}\le.피트({\frac{dt}{dx}}\right)^{-1}=-\left({\frac {dt}{dx}}\right)^{-3}{\frac {d^{2}t}{dx^{2}}}\\[4pt]&={\frac {d}{dx}}\left({\frac {1}{2}}\left({\frac {dt}{dx}}\right)^{-2}\right)\end{aligned}}}$

다시 강조하자면, $t{\displaystyle }$ ${\displaystyle$ t$}$에 $관한$ 두 번째 파생상품이 $x{\displaystyle }$ ${\displaystyle$x$\}$의 파생상품으로 표현되었다는$$ 점이 달성되었다. 이제 원래의 2차 방정식을 통합할 수 있다.

${\displaystyle {\begin{aligned}{\frac {d^{2}x}{dt^{2}}}&=f(x)\\{\frac {d}{dx}}\left({\frac {1}{2}}\left({\frac {dt}{dx}}\right)^{-2}\right)&=f(x)\\\left({\frac {dt}{dx}}\right)^{-2}&=2\int f(x)dx+C_{1}\\{\frac {dt}{dx}}&=\pm {\frac {1}{\sqrt {2\int f(x)dx+C_{1}}}\\t+C_{2}&=\pm \int {\frac {dx}{\sqrt {2\int f(x)dx+C_{1}}}}\end{정렬}}$

이것은 암묵적인 해결책이다. 가장 큰 잠재적 문제는 통합을 단순화할 수 없다는 것이며, 이는 통합 상수를 평가하는 데 어려움이 있거나 불가능함을 의미한다.

특수 케이스: x" = x'ⁿ f(x)

위의 접근법을 이용하여, 우리는 기술을 보다 일반적인 방정식으로 확장할 수 있다.

${\dplaystyle {\frac {d^{2}x}{dt^{2}}=\좌측값\frac {dx}{dt}\오른쪽)^{n}f(x)}$

여기서 $n{\displaystyle }$ ${\displaystyle n}$은(는) 2와 같지 않은 일부 매개 변수다. 이는 두 번째 파생상품이 $x{\displaystyle {}^{}}${$${\$displaystyle$ x$'}$의 힘을 포함하는 형태로 작성될 수 있기 때문에 효과가 있을 것이다. 두 번째 파생상품을 재작성하고, 재배열하며, 왼쪽을 파생상품으로 표현한다$.$

${\displaystyle{\begin{정렬}&, -\left({\frac{dt}{dx}}\right)^{-3}{\frac{{2d^}t}{dx^{2}}}=\leftᆬ^ᆷfᆭ\\[4pt]&, -\left({\frac{dt}{dx}}\right)^{n-3}{\frac{{2d^}t}{dx^{2}}}=fᆯ\\[4pt]&,{\frac{d}{dx}}\left({\frac{1}{2-n}}\left({\frac{dt}{dx}}\right)^{n-2}\right)=fᆱ\\[4pt]&, \left({\frac{dt}{dx}}\right)^{.fn-2}=(2-n)\int(x)dx+C_{1}\\\[2pt]&t+C_{2}=\int \left(2-n)\int \f(x)dx+C_{1}\right)^{\frac {1}{n-2}}dx\end}}}}$

$n{\displaystyle }$ ${\displaystyle n}$이(가) 짝수일 경우 오른쪽에는 +/-가 들어간다. ${\displaystyle \mathrm{n}}$= 2 ${\displaystyle n=2$

${\displaystyle {\begin{aligned}-\left({\frac {dt}{dx}}\right)^{-1}{\frac {d^{2}t}{dx^{2}}}&=f(x)\\-{\frac {d}{dx}}\left(\ln \left({\frac {dt}{dx}}\right)\right)&=f(x)\\{\frac {dt}{dx}}&=C_{1}e^{-\int f(x)dx}\\t+C_{2}&=C_{1}\int e^{-\int f(x)dx}dx\end{aligned}}}$

상위주문

3차 이상의 자율방정식을 푸는 데는 유사한 방법이 없다. 그러한 방정식은 예를 들어, 방정식의 오른쪽이 종속변수에 대해서만^[4][5](즉, 파생상품이 아님) 선형성 또는 의존성과 같은 다른 단순화된 특성을 가지고 있는 경우에만 정확히 해결될 수 있다. 3차원의 비선형 자율 시스템이 로렌츠 끌러나 뢰슬러 끌러와 같은 실로 혼란스러운 행동을 일으킬 수 있다는 점을 고려하면 이는 놀랄 일이 아니다.

이러한 사고방식으로, 2차 순서의 일반적인 비자율 방정식은 또한 혼란스러울 수 있기 때문에 명시적으로 풀 수 없다는 것 또한 그리 놀라운 일이 아니다(이러한 예는 주기적으로 강제되는 진자이다^[6]).

다변량 케이스

${\displaystyle \mathrm{이제}}$ x ${\displaystyle {}^{}}$( t${\displaystyle }$)${\displaystyle }$= ${\displaystyle A}$ ${\displaystyle x\mathbf{}}$( t${\displaystyle }$) ${\displaystyle \mathbf {x} '(t)=$가 있다.$A\mathbf${${\displaystyle x}$$}(t$ $여기$서 x${\displaystyle }$( t${\displaystyle }$) ${\displaystyle \mathbf {x}(t)}$은 t {\$displaystyle$n} -dension$$ column vector는 t ${\displaystyt}$에 종속된 n ${\$displaystyle n$\}$이다.

솔루션은 $x{\displaystyle }$${\displaystyle }$(${\displaystyle t}$ )${\displaystyle }$= e ${\displaystyle A^{}}$ t ${\displaystyle {}^{}\mathbf{}}$ ${\${$c}$이며 여기서 $c$ ${\$ {c}은 n$$${\displaystyle \times }$ ${\displaystyle 1}$ ${\displaysty$ n$\times 1}$ 상수$$ 벡터가 된다$$$.$^[7]

참고 항목

• 시간불변성계통
• 비자율계(수학)

참조