뢰슬러 어트랙터

이 기사는 검증을 위해 추가 인용이 필요합니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 기사를 개선하는 데 도움을 주세요. 출처가 없는 재료는 문제가 발생하여 제거될 수 있습니다. 출처 찾기 : "Rössler attactor" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2013년 6월) (본 템플릿 메시지 제거 방법 및 시기에 대해 알아보기)

뢰슬러 끌개 / ˈr ɒr ər/은 1970년대 오토 뢰슬러가 처음 연구한 3개의 비선형 상미분 방정식 시스템인 뢰슬러 시스템의 끌개입니다. 이러한 미분 방정식은 어트랙터의 프랙탈 특성과 관련된 혼돈 역학을 나타내는 연속 시간 동적 시스템을 정의합니다.^[3] 뢰슬러는 그것을 엿을 끄는 기계의 형식화라고 해석했습니다.^[4]

뢰슬러 시스템의 일부 속성은 고유 벡터와 같은 선형 방법을 통해 추론할 수 있지만 시스템의 주요 기능은 Poincaré 지도 및 분기 다이어그램과 같은 비선형 방법이 필요합니다. 원래의 뢰슬러 논문은 뢰슬러 끌개가 로렌츠 끌개와 비슷하게 행동하도록 의도되었지만 또한 정성적으로 분석하기에 더 쉽다고 말합니다.^[1] 어트랙터 내의 궤도는 불안정한 고정점을 중심으로 ${\displaystyle x,}$ y ${\displaystyle x,y}$ 평면에$$ 가까운 바깥쪽 나선을 따라갑니다. 그래프가 충분히 나선형으로 빠져나가면 두 번째 고정점이 그래프에 영향을$$주어 z {\$display$ z$}$ $차원$의 상승과 비틀림을 유발합니다. 시간 영역에서는 각 변수가 고정된 값 범위 내에서 진동하지만 진동이 혼란스럽다는 것이 분명해집니다. 이 어트랙터는 로렌츠 어트랙터와 몇 가지 유사점이 있지만 더 단순하고 매니폴드가 하나만 있습니다. 오토 뢰슬러는 1976년에 뢰슬러 끌개를 설계했지만,^[1] 원래의 이론 방정식은 나중에 화학 반응의 평형 모델링에 유용한 것으로 밝혀졌습니다.

정의.

뢰슬러 계의 정의식은 다음과 같습니다.^[3]

${\displaystyle {\begin{case}{\frac {dx}{dt}}=-y-z\\{\frac {dy}{dt}}=x+ay\{\frac {dz}{dt}}=b+z(x-c)\end{case}}}$

Rössler는 = ${\displaystyle 0.}$2 {\displaystyle a=$0인$ 혼돈 어트랙터를 연구했습니다$.$$2$ $b$ $=$ 0$.$ {\displaystyle b$=$$0$입니다.$2}$및 $c$ $=$ 5$.7$ {\$displaystyle$ $c$ $=$${\displaystyle }$5.7$},$ a $=$ 0.1 {\displaystyle a $=$ 0.1}, b $=$ 0.1 {\displaystyle b $=$ 0.1} 및 c $=$ 14 {\displaystyle c $=$ 14}의 속성이 이후 더 일반적으로 사용되고 있습니다. 위상 분석을 사용하여 매개변수 공간의 다른 라인을 조사했습니다. $b$ = ${\$$displaystyle$ b=2}, c = 4 {\displaystyle c=4}에 해당하며 분기 파라미터로 {\displaystyle a}을 선택했습니다. 뢰슬러가 어떻게 이 방정식들을 발견했는지는 르텔리에와 메세저에 의해 조사되었습니다.^[6]

안정성 분석

뢰슬러 어트랙터의 우아함 중 일부는 방정식 중 두 개가 선형이기 때문입니다. $z$ = ${\displaystyle 0}$ ${\$displaystyle z = 0}을(를) 설정하면 x, y {\displaystyle x,y} 평면에서 동작을 검사할 수 있습니다.

${\displaystyle {\begin{case}{\frac {dx}{dt}}=-y\{\frac {dy}{dt}}=x+ay\end{case}}}$

The stability in the ${\displaystyle x,y}$ plane can then be found by calculating the eigenvalues of the Jacobian ${\displaystyle {\begin{pmatrix}0&-1\\1&a\\\end{pmatrix}}}$, which are ${\displaystyle (a\pm {\sqrt {a^{2}-4}})/2}$. From this, < < ${\displaystyle$ 0$<a<2$일 때 고유값은 복잡하고 둘 다 양의 실제 성분을 가지므로 $x{\displaystyle ,}$ ${\displaystyle y}$ ${\displaystyle x,y}$ 평면의$$ 바깥쪽 나선으로 원점이 불안정하다는 것을 알 수 있습니다. Now consider the ${\displaystyle z}$ plane behavior within the context of this range for ${\displaystyle a}$. So as long as ${\displaystyle x}$ is smaller than ${\displaystyle c}$, the ${\displaystyle c}$ term will keep the orbit close to the ${\displaystyle x,y}$ plane. $궤도$가 $c{\displaystyle }$ ${\displaystyle c}$보다 큰 $x{\displaystyle }$ ${\displaystyle$ x$}$에 가까워지면$$z ${\displaystyle$ z$}$ - $값$이 상승하기 시작합니다. $그러나{\displaystyle }$ z ${\displaystyle$ z$}$이(가) 상승하면${\displaystyle }$${\displaystyle \mathrm{dx}}$ $dt$ {\$displaystyle$dx$/dt$}에 있는 -z$$ ${\displaystyle -z}$이(가)$x$ {\$displaystyle$ x$}$의 증가를$$ 중지합니다$.$

고정점

고정점을 찾기 위해 3개의 뢰슬러 방정식을 0으로 설정하고 결과 방정식을 풀어서 각 고정점의 (${\displaystyle }$ ${\displaystyle x$ ${\displaystyle }$ ${\displaystyle$ y$\},$ ${\displaystyle }$ ${\displaystyle$ z$\})$ 좌표를 결정했습니다. 다음과 같은 각 고정점 좌표의 일반적인 방정식을 얻을 수 있습니다.^[7]

${\displaystyle {\begin{cases}x={\frac {c\pm {\sqrt {c^{2}-4ab}}}{2}}\\y=-\left({\frac {c\pm {\sqrt {c^{2}-4ab}}}{2a}}\right)\\z={\frac {c\pm {\sqrt {c^{2}-4ab}}}{2a}}\end{cases}}}$

다음과 같이 매개변수 값 집합의 실제 고정점을 표시하는 데 사용할 수 있습니다.

${\displaystyle \left({\frac {c+{\sqrt {c^{2}-4ab}}}{2}},{\frac {-c-{\sqrt {c^{2}-4ab}}}{2a}},{\frac {c+{\sqrt {c^{2}-4ab}}}{2a}}\right)}$

${\displaystyle \left({\frac {c-{\sqrt {c^{2}-4ab}}}{2}},{\frac {-c+{\sqrt {c^{2}-4ab}}}{2a}},{\frac {c-{\sqrt {c^{2}-4ab}}}{2a}}\right)}$

위의 Rössler Attactor의 일반적인 그림에서 볼 수 있듯이 이러한 고정점 중 하나는 Attactor 루프의 중심에 있고 다른 하나는 Attactor에서 상대적으로 멀리 떨어져 있습니다.

고유값과 고유벡터

이 고정점들 각각의 안정성은 각각의 고유값과 고유벡터를 결정함으로써 분석될 수 있습니다. 야코비안부터 시작합니다.

${\displaystyle {\begin{pmatrix}0&-1&-1\\1&a&0\\z&0&x-c\\\end{pmatrix}}}$

고유값은 다음과 같은 입방정계를 풀어서 구할 수 있습니다.

${\displaystyle -\lambda ^{3}+\lambda ^{2}(a+x-c)+\lambda(ac-ax-1-z)+x-c+az=0\,}$

중앙에 위치한 고정점의 경우 뢰슬러의 원래 매개변수 값인 a=0.2, b=0.2 및 c=5.7은 다음과 같은 고유값을 산출합니다.

${\displaystyle \lambda _{1}=0.0971028+0.995786i\,}$

${\displaystyle \lambda _{2}=0.0971028-0.995786i\,}$

${\displaystyle \lambda _{3}=-5.68718\,}$

음의 고유 값의 크기는 해당 고유 벡터를 따라 인력 수준을 특징으로 합니다. 마찬가지로 양의 고유 값의 크기는 해당 고유 벡터를 따라 반발 수준을 특징으로 합니다.

이 고유값에 해당하는 고유 벡터는 다음과 같습니다.

${\displaystyle v_{1}={\begin{pmatrix}0.7073\\-0.07278-0.7032i\\0.0042-0.0007i\\\end{pmatrix}}}$

${\displaystyle v_{2}={\begin{pmatrix}0.7073\\0.07278+0.7032i\\0.0042+0.0007i\\\end{pmatrix}}}$

${\displaystyle v_{3}={\begin{pmatrix}0.1682\\-0.0286\\0.9853\\\end{pmatrix}}}$

이 고유 벡터는 몇 가지 흥미로운 의미를 가지고 있습니다. 첫째, 어트랙터의 메인 디스크에서 발생하는 안정적인 외부 슬라이드는 두 고유값/고유 벡터 쌍(${\displaystyle {v1\mathrm{}}_{}}$ ${\$ 및$$ ${\displaystyle {v2\mathrm{}}_{}}$ ${\$에 의해 담당됩니다. 마지막 고유값/고유벡터 쌍은 매니폴드의 중심을 통과하고 어트랙터 내에서 발생하는 z 운동을 설명하는 축을 따라 끌립니다. 이 효과는 아래 그림을 통해 대략적으로 입증됩니다.

그림은 중앙 고정점 고유 벡터를 조사합니다. 파란색 선은 = ${\displaystyle 0.2}${\display style a=$0$으로 생성된 표준 Rössler 끌개에 해당합니다$.$$2$ $b$ $=$ 0$.$ {\displaystyle b$=$$0$입니다.$2$ $c$ $=$ $7$ {\$displaystyle$ c $=$ 5.7$\}.$ 이 어트랙터의 중앙에 있는 빨간색 점은 FP 1 {\displaystyle FP_{1}}입니다. 이 고정점과 교차하는 빨간색 선은 ${\displaystyle {v1\mathrm{}}_{}}$ ${\$ 및$$ ${\displaystyle {v2\mathrm{}}_{}}$ ${\$에 의해 생성된 반발 평면의 그림입니다$.$ 초록색 선은 매력적인 ${\displaystyle {v3\mathrm{}}_{}}$ {\$displaystyle$ v_${3}}$의 그림입니다$.$ 마젠타 선은 ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$보다 약간 위에 있는 끌림 고유 벡터의 한 점에서 시간이 지남에 따라 뒤로 물러나 생성됩니다.$$ 이는 해당 벡터에 의해 완전히 지배되는 점의 동작을 보여줍니다. 마젠타 선은 고정점 위로 당겨지기 전에 어트랙터의 평면에 거의 닿습니다. 이는 뢰슬러 어트랙터의 일반적인 모습과 동작이 어트랙터 ${\displaystyle {v3\mathrm{}}_{}}$ ${\$과 반발 ${\displaystyle {v1\mathrm{}}_{}}$ ${\$} 사이의 상호 작용의 산물임을 시사합니다.$v_{1}}$ 및$$ ${\displaystyle {v2\mathrm{}}_{}}$ ${\$ 평면입니다$$. 특히 뢰슬러 방정식에서 생성된 시퀀스가 ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ 주위를 루프하기 시작하고$$${\displaystyle {v3\mathrm{}}_{}}$ ${\$ 벡터$$ 위로 당겨지기 시작함을 의미합니다. 벡터를 향해 안쪽으로 약간 휘어진 곡선의 위쪽 팔을 만들고 다시 밖으로 밀려나면서 반발면을 향해 잡아당깁니다.

이상점 고정점의 경우 뢰슬러의 원래 매개변수 $값$인 a =${\displaystyle 0.2}$ ${\$display a = $0입니다.$$2$ $b$ $=$ 0$.$ {\displaystyle b$=$$0$입니다.$2$$\},$ c $=$ $7$ {\displaystyle c $=$ 5.7}의 고유값이 산출됩니다.

${\displaystyle \lambda _{1}=-0.0000046+5.4280259i}$

${\displaystyle \lambda _{2}=-0.0000046-5.4280259i}$

${\displaystyle \lambda _{3}=0.1929830}$

이 고유값에 해당하는 고유 벡터는 다음과 같습니다.

${\displaystyle v_{1}={\begin{pmatrix}0.0002422+0.1872055i\\0.0344403-0.0013136i\\0.9817159\\\end{pmatrix}}}$

${\displaystyle v_{2}={\begin{pmatrix}0.0002422-0.1872055i\\0.0344403+0.0013136i\\0.9817159\\\end{pmatrix}}}$

${\displaystyle v_{3}={\begin{pmatrix}0.0049651\\-0.7075770\\0.7066188\\\end{pmatrix}}}$

이러한 고유 값과 고유 벡터가 뢰슬러 어트랙터에 존재하지만, 이들의 영향은 초기 조건이 이 이상치 고정점 근처에 있는 뢰슬러 시스템의 반복에 국한됩니다. 초기 조건이$$λ 1 ${\displaystyle \lambda$ _{${\displaystyle 1_{}}$}}$$및 λ 2${\displaystyle$\lambda _{2}}에 의해 생성된 끌림 평면에 있는 경우를 제외하고, 이러한 영향은 결과적인 시스템을 일반 뢰슬러 끌림기 쪽으로 밀어내는 것을 포함합니다. 결과적인 시퀀스가 중앙 고정점과 어트랙터 자체에 접근함에 따라 이 먼 고정점(및 고유 벡터)의 영향이 줄어들 것입니다.

푸앵카레 지도

Poincaré 지도는 특정 방향으로 설정된 평면을 통과할 때마다 함수의 값을 플롯하여 구성됩니다. 예를 들어 $x$ = ${\$$displaystyle$ x = 0} 평면을 통과할 $때$마다 y${\displaystyle ,}$ ${\displaystyle z}$ ${\displaystyle$ y$,z}$ 값을 표시하고, 여기서 x {\displaystyle x}는 음수에서 양수로 변경되며, 일반적으로 로렌츠 어트랙터를 연구할 때 수행됩니다. 뢰슬러 어트랙터의 경우 $뢰슬러$ 방정식의 특성상 맵이 $항상$ z = 0 {\displaystyle x = 0}에서 x = 0 {\displaystyle x = 0} 평면을 가로지르기 때문에 x = ${\displaystyle 0}$ ${\$displaystyle x = 0}$$은 흥미롭지 않습니다. In the ${\displaystyle x=0.1}$ plane for ${\displaystyle a=0.1}$, ${\displaystyle b=0.1}$, ${\displaystyle c=14}$, the Poincaré map shows the upswing in ${\displaystyle z}$ values as ${\displaystyle x}$ increases, 뢰슬러 플롯의 업스윙 및 트위스트 섹션으로 인해 예상됩니다. 이 특정 Poincaré 그림의 점 수는 무한대이지만 다른 $c{\displaystyle }$ ${\displaystyle c}$ 값을$$ 사용하면 점 수가 달라질 수 있습니다. 예를 들어, $c{\displaystyle }${\$displaystyle$c} 값이$$ 4인 경우, 함수가 주기 1의 주기 궤도를 산출하거나 c ${\displaystyle$ c$}$ 값이$$ $12{\displaystyle }$.8로 설정된 경우 주기 6 궤도에 해당하는 점이 6개가 됩니다.

로렌츠 지도

로렌츠 지도는 궤적에서 좌표의 연속적인 최대치 사이의 관계입니다. 끌개에 대한 궤적을 고려하고 $x{\displaystyle {}_{}}$ ${\displaystyle {\max }_{}}$(${\displaystyle n)}$ ${\displaystyle x_{max}(n)}$를 x 좌표의 n번째 최대값이라고 가정합니다. Then ${\displaystyle x_{max}(n)}$-${\displaystyle x_{max}(n+1)}$ scatterplot is almost a curve, meaning that knowing ${\displaystyle x_{max}(n)}$ one can almost exactly predict ${\displaystyle x_{max}(n+1)}$.^[8]

로컬 최대치 매핑

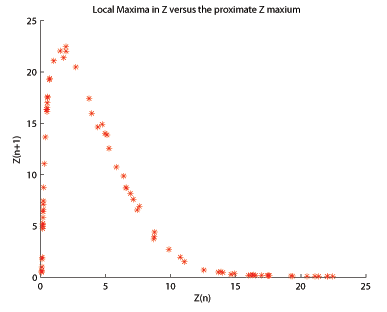
로렌츠 어트랙터에 대한 원본 논문에서 에드워드 로렌츠는 바로 앞에 있는 로컬 $최대치$에 대해$$ $z{\displaystyle }$ ${\displaystyle$ z$}$의 로컬 최대치를 분석했습니다.^[9] 시각화했을 때, 이 플롯은 텐트 맵과 유사했으며, 이는 지도와 어트랙터 사이에 유사한 분석을 사용할 수 있음을 암시합니다. 뢰슬러 어트랙터의 경우 z ${\displaystyle n_{}}$ ${\displaystyle z_{n}}$ 로컬 최대값이 다음 로컬 $z$ ${\displaystyle$ z}$최대값$인 $z$ n +${\displaystyle 1_{}}$ ${\displaystyle z_${n$+1}에$대해 표시되면$$결과 그림(a =$0.2$ {\$displaystyle$ a = 0인 경우 $여기$ shown)이 표시됩니다.$2$ $b$ $=$ 0$.$ {\displaystyle b$=$$0$입니다.$2$ $c$ $=$ $7$ {\displaystyle c $=$ 5.7})은 비대칭 헤논 맵과 유사한 단일 모드입니다. 뢰슬러 어트랙터를 사용하여 의사 1-d 지도를 만들 수 있음을 알고 유사한 분석 방법을 사용합니다. 분기 다이어그램은 특히 유용한 분석 방법입니다.

매개변수의 변화

뢰슬러 어트랙터의 행동은 주로 상수 $매개변수{\displaystyle }$ a ${\displaystyle a},$$b{\displaystyle }$ ${\displaystyle$ b}$및$$c{\displaystyle }$ ${\displaystyle$ c}$값$의 요인입니다$.$ 일반적으로 각 매개변수를 변경하면 시스템이 주기적 궤도, 고정점 또는 무한대로 탈출하는 데 수렴하여 유사한 효과가 있습니다. 그러나 각 파라미터에 따라 유도되는 특정 범위 및 동작은 상당히 다릅니다. 뢰슬러 시스템의 주기적 궤도 또는 "단위 사이클"은 고리 시리즈가 반복되기 시작하기 전에 중심점을 중심으로 발생하는 고리의 수에 의해 정의됩니다.

분기 다이어그램은 동적 시스템의 거동을 분석하기 위한 일반적인 도구이며, 그 중 뢰슬러 어트랙터는 하나입니다. 변수 중 하나를 제외한 모든 변수를 일정하게 유지하고 마지막 변수를 변경하여 시스템의 방정식을 실행함으로써 생성됩니다. 그런 다음 과도 요인이 중화된 후 변경된 변수의 특정 값이 방문하는 점을 그래프로 표시합니다. 혼돈 영역은 그림의 채워진 영역으로 표시됩니다.

변주 a

여기서 $b{\displaystyle }$ ${\displaystyle b}$는 0.2로 $고정$되고$$c {\$displaystyle$ c$$$}$는 5.7로 고정되며 ${\displaystyle$ a$}$는 변경됩니다. ${\displaystyle a}$을(를) 변경하는 동안 어트랙터의 동작을 수치로 조사한 결과 어트랙터의 동작에 불균형적인 영향을 미치는 것으로 나타났습니다$$. 분석 결과는 다음과 같습니다.

• ${\displaystyle \mathrm{a}}$ ${\displaystyle \le }$ 0 ${\displaystyle a\leq 0}$: 중앙에 위치한 고정점으로 수렴합니다.
• ${\displaystyle a}$$1}$: 1교시 단위주기
• ${\displaystyle a}$$2}$: 뢰슬러가 선택한 표준 매개변수 값, 혼돈
• ${\displaystyle a}$$3}$: 혼란스러운 어트랙터, 훨씬 더 뫼비우스 띠 모양(자신을 접는 것).
• ${\displaystyle a}$ = $35$ {\displaystyl${\displaystyle e}$ a = 0.35} : .3과 비슷하지만 점점 더 혼란스러워짐
• ${\displaystyle a}$$38}$: .35와 비슷하지만 점점 혼란스러워집니다.

변주 b

$여기$서 ${\displaystyle a}$는 0.2로 고정되고$$, $c{\displaystyle }$ ${\displaystyle$ c$}$는 5.7로 $고정$되며,$$b {\$displaystyle$ b$}$는 변경됩니다$$. 첨부된 다이어그램에서 볼 수 있듯이, $b{\displaystyle }${\$displaystyle$ b$}$가 0에$$ 가까워지면 어트랙터는 무한대에 접근합니다($b{\displaystyle }$ ${\displaystyle$ b$}$의 매우 작은 값에 대한 상승에 주목하십시오$).$ $다른{\displaystyle }$ 매개변수와 비교하여 b$${\$displaystyle$b}를 변경하면 주기-3 및 주기-6 궤도가 발생할 때 더 큰 범위가$$ 생성됩니다. ${\displaystyle a}$ 및$$ $c{\displaystyle }$ ${\displaystyle c}$와 달리 b ${\displaystyle b}$의 값이 높을수록 혼돈 상태가 아닌 period-1로 수렴합니다$.$

변주 c

여기서 $a$ = ${\displaystyle b}$ = 0.1 ${\displaystyle$a = b = 0.1} 및 $c$ ${\displaystyle$ c$}$ 가 변경됩니다. 분기 다이어그램에 $따르면{\displaystyle }$ c$${\$displaystyle$c}의 낮은 값은 주기적이지만$$ $c{\displaystyle }${\$displaystyle c}$가 증가함에 따라 빠르게 혼란스러워집니다. $이{\displaystyle }$ 패턴은 c ${\displaystyle c}$가 증가함에 따라 반복됩니다. 혼돈 기간과 함께 주기성의 섹션이 있으며 $c{\displaystyle }$ ${\displaystyle c}$가 증가함에 따라 더 높은 주기 궤도로 향하는 추세입니다. 예를 들어, 한 궤도의 주기는 4 $주변$의 c ${\displaystyle$ c$}$ 값에 대해서만 나타나며 분기 다이어그램에서는 다시 찾을 수 없습니다. 주기 3에서도 동일한 현상이 $관찰$됩니다. ${\displaystyle \mathrm{c}}$ =$$12 {\displaystyle c = 12}까지는 주기 3 궤도를 찾을 수 있지만 그 이후에는 나타나지 않습니다.

$c{\displaystyle }$ ${\displaystyle c}$ 값$$ 범위에 걸쳐 변화하는 끌개의 그래픽 그림은 주기성과 비주기성 사이의 빈번한 전환이라는 이러한 모든 매개변수 분석에서 볼 수 있는 일반적인 동작을 보여줍니다.

위의 이미지 세트는 $c{\displaystyle }$ ${\displaystyle c}$가 다양한 값 범위에서 변화함에 따라 과도 후 뢰슬러 시스템의 변화를 보여줍니다. $이$ 이미지는 a = ${\displaystyle b}$ = .${\displaystyle 1}$ {\$displaystyle$ a = b = .1}로 생성되었습니다$.$

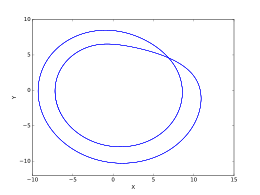
• ${\displaystyle c}$ = ${\displaystyle 4}${\displaystyl${\displaystyle e}$ c = 4}, 주기-1 궤도.
• ${\displaystyle c}$ = ${\displaystyle 6}${\displaysty${\displaystyle l}$e c=6}, 주기-2 궤도.
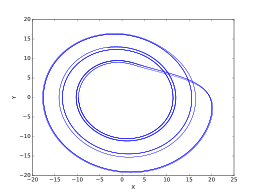
• ${\displaystyle c}$ = $5$ {\displaystyl${\displaystyle e}$ c = 8.5}, 주기-4 궤도.
• ${\displaystyle c}$ = $7$ {\displaystyl${\displaystyle e}$ c = 8.7}, 주기-8 궤도.
• ${\displaystyle c}$ = ${\displaystyle 9}${\displaystyl${\displaystyle e}$ c = 9}, 희소 혼돈 어트랙터.
• ${\displaystyle c}$ = ${\displaystyle 12}${\displaystyl${\displaystyle e}$ c = 12}, 주기-3 궤도.
• ${\displaystyle c}$ = $6$ {\displaystyl${\displaystyle e}$ c = 12.6}, 주기-6 궤도.
• ${\displaystyle c}$ = ${\displaystyle 13}${\displaystyl${\displaystyle e}$ c = 13}, 희소 혼돈 어트랙터.
• ${\displaystyle c}$ = ${\displaystyle 18}${\displaystyl${\displaystyle e}$ c = 18}, 혼란스러운 어트랙터가 가득합니다.

주기궤도

어트랙터는 주기적인 궤도로 조밀하게 채워져 있습니다: $x$ →${\displaystyle }$($t$+${\displaystyle T}$) = x → (t) {\displaystyle {\vec {x}}(t+T) = {\vec {x}(t)}와 같은 $T$ ${\displaystyle T}$의 0이 아닌 값이 존재합니다. 뉴턴의 방법을 사용하면 이 흥미로운 해들을 수치적으로 유도할 수 있습니다. 주기적 궤도는${\displaystyle {}_{}}$φ t$$- Id ${\displaystyle \Phi$_$\{$t}-Id} 함수의 $뿌리$이며$,$ ${\displaystyle {여기}_{}}$서 φ t${\displaystyle$ \Phi _{t}}는 $시간 t${\$t$}에 의한$진화$이며 $Id {\$displaystyle Id}는 항등식입니다. 역학의 대부분이 x-y 평면에서 일어나기 때문에 주기적 궤도는 투영 후 중앙 평형을 중심으로 한 권선 수에 의해 분류될 수 있습니다.

수치 실험을 통해 모든 양의 권선 수에 대해 고유한 주기 궤도가 존재하는 것으로 보입니다. 이러한 퇴행성의 결여는 아마도 그 문제의 대칭성의 결여 때문일 것입니다. 어트랙터는 1D 주기 궤도와 2D 안정 및 불안정 주기 궤도의 불변 다양체로 분해할 수 있습니다. 이 불변 다양체들은 유리수가 실수에 있는 것과 마찬가지로 끌개의 자연스러운 뼈대입니다.

동적 시스템 이론의 목적을 위해 이러한 다양체의 위상 불변성에 관심을 가질 수 있습니다. 주기 궤도는 R ${\displaystyle {\mathrm{}}^{}}$ ${\$에 내장된 $S{\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$ ${\$ S$^{1}}$의 사본이므로$$매듭 이론으로 위상 특성을 이해할 수 있습니다. 1번과 2번이 감긴 주기적인 궤도는 Hopf 연결을 형성하며, 어떠한 형태도 이 궤도들을 분리할 수 없음을 보여줍니다.

다른 주제 링크

뢰슬러 끌개에서 잘 보이는 밴딩은 칸토어 집합이 중간 지점을 중심으로 회전한 것과 유사합니다. 또한, 뢰슬러 어트랙터에서 발생하는 반 트위스트는 어트랙터의 일부에만 영향을 미칩니다. 뢰슬러(Rössler)는 실제로 그의 인력이 "정상 밴드"와 뫼비우스 띠의 조합이라는 것을 보여주었습니다.^[10]

참고문헌

외부 링크

• PovRay를 이용한 플래시 애니메이션
• 로슬러 1976.pdf
• 로렌츠와 뢰슬러 어트랙터 – 자바 애니메이션
• 3D 어트랙터: Rössler 및 Lorenz 어트랙터를 3차원으로 시각화하고 탐색하는 Mac 프로그램
• 스콜라피디아의 뢰슬러 어트랙터
• Rössler Attactor : 3D 수치 상호작용 실험 - experiences.math.cnrs.fr - ( jav스크립트/webgl)