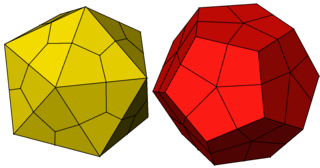
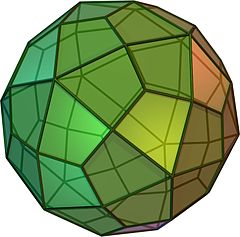
델토이탈 육면체

델토이탈 육면체
(모델을 회전하려면 여기를 클릭하십시오.)
유형	카탈루냐 주
콘웨이 표기법	oD 또는 deD
콕시터 다이어그램
면 폴리곤	연을
얼굴	60
가장자리	120
정점	62 = 12 + 20 + 30
면 구성	V3.4.5.4
대칭군	Ih, H3, [5,3], (*532)
회전군	I, [5,3]+, (532)
디헤드각	154° 7° 17° 아크코(Acco)-19-8√5/41)
특성.	볼록한, 얼굴-변형
롬비코시도데코헤드론 (이중 다면체)	그물

기하학에서, 망상성 육면체(사다리꼴성 육면체, 스트롬비크성 육면체 또는 사방형 육면체라고도^[1] 함)는 카탈로니아 고체로, 아르키메데스 고체인 롬비코시도데카헤드론의 이중 다면체다. 정점 중 해밀턴의 경로가 없는 것은 6개의 카탈로니아 고형물 중 하나이다.^[2]

그것은 위상학적으로 비콘벡스 헥세콘헤드론과 동일하다.

길이와 각도

60개의 얼굴은 델토이드나 연이다. 각 연의 짧고 긴 가장자리는 1:7 + √5/6 ≈ 1:1.539344663...

한 면의 짧은 두 가장자리 사이의 각도는 아크코(-5-2√5/20)118.2686774705° 긴 가장자리 사이의 반대각은 arccos(-5+9√5/40)67.783011547435°이다. 각 면의 다른 두 각도는 각각 짧은 가장자리와 긴 가장자리 사이에 있으며, ar86.97415549104°와 같다.

인접 면의 쌍 사이의 이음각은 아크코(-19-8√5/41)154.1236312578°

위상

토폴로지로는 탈모성 육면체(Deltoale hexecontahedron)가 비콘벡스 롬빅 육면체와 동일하다. 델토이탈 육면체는 얼굴 중심, 가장자리 중심 및 정점을 신체 중심에서 다른 반경으로 밀어내 도데카헤드론(또는 이코사헤드론)에서 유도할 수 있다. 반지름은 그 결과의 모양이 정점이 도-3 코너로 가고, 도 5 코너로 가고, 가장자리의 중심이 도 4 포인트로 가는 평면 연을 향하도록 선택된다.

직교 투영

델토이탈 육각면체에는 3개의 대칭 위치가 정점의 세 가지 유형에 위치한다.

직교 투영

투영적 대칭	[2]	[2]	[2]	[2]	[6]	[10]
이미지
이중 이미지

변형

델토이탈 육면체는 정점 중간과 중간 면에 정점을 더하고 각 가장자리 중심에서 안면 중심까지 새로운 가장자리를 만들어 일반 이코사면 또는 일반 도데면체에서 구성될 수 있다. 콘웨이 다면체 표기법은 이를 oI, oD, icosaheadron, opho-do-deadheadron으로 나타낼 것이다. 이러한 기하학적 변화는 자유도를 따라 연속체로 존재한다.

관련 다면체 및 틸팅

균일한 이두면체 다면체 계열
대칭: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
이중에서 균일한 폴리헤드라까지
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

구에 투영될 때(오른쪽 참조) 가장자리가 이두면체와 도두면체의 가장자리를 이중으로 배열한 것을 알 수 있다.

이 타일링은 표면상(V3.4.n.4)과 함께 망상성 다면체(Deltoal polyedra)의 일부로서 위상학적으로 연관되며 쌍곡면의 기울기로 계속된다. 이러한 얼굴-변환 수치는 반사 대칭(*n32)을 가진다.

*n32 이중 확장 틸팅의 대칭 돌연변이: V3.4.n.4

대칭 *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라코.
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
피겨 구성.	V3.4.2.4	V3.4.3.4	V3.4.4.4	V3.4.5.4	V3.4.6.4	V3.4.7.4	V3.4.8.4	V3.4.168.4

참고 항목

• 델토이탈 이코시테트라헤드론

참조

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3-9)절)
• 2008년 사물의 대칭, 존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, ISBN 978-1-56881-220-5[1] (21장, 아르키메데스 및 카탈로니아 다면체의 명명 및 기울기, 286쪽, 4각형 육면체면체)
• http://mathworld.wolfram.com/ArchimedeanDualGraph.html

외부 링크

• Eric W. Weisstein, DeltoidalHexecontahedron and Hamiltonian path (Catalan solid) at MathWorld.
• Deltoidal Hexecontahedron (Trapezoidal Hexecontrahedron)—대화형 다면체 모델
• 실제 생활에서의 예—리프스톱 나일론으로부터 직경이 거의 4미터에 이르고 바람에 의해 부풀어 오른 공. 그것은 아이들이 연 축제에서 그것을 가지고 놀 수 있도록 땅바닥에서 튕겨나간다.