삼면체

삼면체
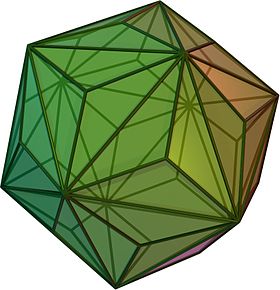(회전 모델을 보려면 여기를 클릭)
유형	카탈로니아 솔리드
콕서터 다이어그램
콘웨이 표기법	kI
얼굴형	V3.10.10 이등변 삼각형
얼굴	60
가장자리	90
꼭지점	32
유형별 정점	20{3}+12{10}
대칭군	Ih, H3, [5,3], (*532)
로테이션 그룹	I, [5,3]+, (532)
이면각	160°36′45″ 아크코스24 + 15 인치5/61)
특성.	볼록한 얼굴 전이성
잘린 12면체 (입체 다면체)	그물

기하학에서, 트라이아키스 20면체(또는 키시코사면체^[1])는 아르키메데스의 이중 고체 또는 카탈로니아 고체이다.그것의 이중은 잘린 12면체이다.

데카르트 좌표

$【\displaystyle \phi】$를 황금비율로 합니다.$({\displaystyle }$ ${\displaystyle 0}$, ±${\displaystyle 1}$, ± ${\displaystyle )}$ )$${$displaystyle$($0$, \$pm$ 1, $\pm \phi$)} 및$$ 이러한 좌표의 순환 순열은 정십이면체의 정점이다.모서리가 직각으로 20면체의 모서리와 교차하는 이중 정십이면체는 점${\displaystyle (\pm 1}$,${\displaystyle }$±${\displaystyle 1}$, ±${\displaystyle 1}$ $)(\$${\displaystyle \mathrm{pm}}$ 1$,\pm$ 1$,\$${\displaystyle pm}$$$1)과 점${\displaystyle (\pm ,,}$ ±${\displaystyle 1}$ /${\displaystyle }$,,${\displaystyle 0}$)($표시$ 스타일$(\pm \phi,\pm$1/$phi,0)$ 및$$ 순환 좌표들을 정점으로 가진다.이 12면체의 모든 좌표에 (${\displaystyle \mathrm{7\mu }}$-${\displaystyle 1}$)${\displaystyle }$/ ${\displaystyle 11}$ ${\displaystyle †0.938}$ ${\displaystyle 748}$ ${\displaystyle 901}$ 93${{style$ (7\phi -1$)/11\$약 0$.938,748,901,93)$의 인수를 곱하면 약간 더 작은 12면체를 얻을 수 있다.이 12면체의 꼭지점 20개는 이십면체의 꼭지점과 함께 원점을 중심으로 하는 삼면체의 꼭지점입니다.긴 모서리의 길이는 2$({디스플레이 2$입니다. 면은 ${\displaystyle \mathrm{아크코}}$ 1개의 둔각 θ (-${\displaystyle 3\theta /}$ ${\displaystyle 10)119}$ 119.${\displaystyle 009}$ 350 ${\displaystyle {869}^{}}$ 29${\$ \$displaystyle$\$arccos$(-$3\phi$/$10)$ \ 약$119.009, 350, 869, 29^{circ}$os 2개의 ${\displaystyle \mathrm{아로}}$ 되어 있습니다$$.$\arccos(\displaystyle \arcos(\phi$+7)/$10)\약$ 30.$199, 324,$ 565, $36$^{\display $\}.$이들 삼각형의 긴 모서리와 짧은 모서리 사이의 길이 ${\displaystyle 비}$는 (${\displaystyle }$7${\displaystyle }$+${\displaystyle 7}$ ) / 5${\displaystyle \mathrm{1\; 1}}$.${\displaystyle 723}$ ${\displaystyle 606}$ ${\displaystyle 797}$75 (\$phi +7$) / 5 \ 약$1.723, 606, 797$ $75 )$입니다$.{\displaystyle }$

직교 투영

삼면체 20면체에는 정점에 두 개, 미드데지에 한 개 등 세 가지 대칭 위치가 있습니다.트라이아키스 20면체에는 정점을 중심으로 한 5개의 특별한 직교 돌기가 두 개의 모서리에 있고, 두 개의 면(육각형과 오각형)이 있습니다.마지막 두 개는 A와₂₂ H 콕서터 평면에 해당합니다.

와이어프레임 모드의 직교 투영

투사적 대칭	[2]	[6]	[10]
이미지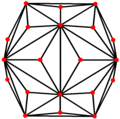
듀얼 이미지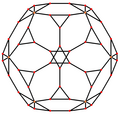

크리토페

그것은 각 면에 삼각형 피라미드가 추가된 20면체, 즉 이십면체의 클라이토프라고 볼 수 있다.이 해석은 triakis라는 이름으로 표현된다.

만약 중심 이십면체를 제거하지 않고 이십면체를 사면체로 증가시킨다면, 이십면체 피라미드의 그물을 얻게 된다.

기타 삼면체

이 해석은 높이가 다른 피라미드를 가진 다른 유사한 비볼록 다면체에도 적용될 수 있다.

• 20면체 또는 작은 3암빅 20면체 또는 때로는 트라이아키스 20면체(다른 것 중)라고 불리는 첫 번째 스테어링
• 큰 12면체(높은 피라미드 포함)
• 12면체(역 피라미드 포함)

스텔레이션

삼면체 20면체에는 이것과 같은 수많은 계단식이 있다.

관련 다면체

균일한 20면체 다면체군
대칭: [5,3], (*532)							[5,3]+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr {5,3}
이중에서 균일한 다면체
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.5

삼면체 20면체는 쌍곡면으로 확장되는 다면체와 타일링의 시퀀스의 일부입니다.이러한 면 전이 수치는 반사 대칭(*n32)을 가집니다.

*n32 잘린 타일링 대칭 변환: t{n,3} v t
대칭 *n32 [n,3]	구면				유클리드	콤팩트 쌍곡선		파라코	비콤팩트 쌍곡선
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
잘렸다 수치
기호.	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{buffic,3}	t{12i,3}	t{9i,3}	t{6i,3}
트리아키스 수치
설정.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3 . v∞ ★

「 」를 참조해 주세요.

• 삼면체 20면체가 극단적인 경우를 제시하는 코치히그 정리
• 트라이아키스 삼각형 타일링으로 다른 "트리아키스" 다면체 형태를 나타냅니다.
• 대삼면체

레퍼런스

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (제3절부터 제9절까지)
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
• Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 0730208. (13개의 반정형 볼록 다면체와 그 쌍체, 19페이지, 삼면체)
• The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, ISBN 978-1-56881-220-5 [1] (21장, 아르키메데아 및 카탈로니아 다면체와 타일링 명명, 284페이지, 트라이아키스 이면체)

외부 링크

• Eric W. Weisstein, Triakis icosahedron (Catalan solid) at MathWorld.
• Triakis 이십면체 – 인터랙티브 다면체 모형