민감도 분석

민감도 분석은 수학적 모델 또는 시스템(숫자 또는 다른 방식)의 출력의 불확실성을 어떻게 나누어 입력의 불확실성의 다른 원천에 할당할 수 있는지에 대한 연구입니다.관련 관행으로는 불확실성 분석이 있는데, 불확실성 정량화와 불확실성 전파에 더 중점을 두고 있으며, 이상적으로 불확실성과 민감도 분석을 병행해야 합니다.

민감도 분석 하에서 변수의 영향을 결정하기 위한 대체 가정 하에서 결과를 다시 계산하는 프로세스는 다음과 같은 다양한 ^[1]목적을 위해 유용할 수 있습니다.

• 불확실성이 존재하는 경우 모델 또는 시스템 결과의 강건성을 테스트합니다.
• 시스템 또는 모델에서 입력 및 출력 변수 간의 관계에 대한 이해를 높입니다.
• 결과에 상당한 불확실성을 야기하는 모델 입력의 식별을 통한 불확실성 감소는 (아마도 추가 연구에 의해) 견고성을 높이기 위해 주의의 초점이 되어야 합니다.
• 입력과 출력 사이에 예기치 않은 관계가 발생하여 모델에서 오류를 검색합니다.
• 모델 단순화 – 출력에 영향을 미치지 않는 모델 입력을 수정하거나 모델 구조의 중복된 부분을 식별하여 제거합니다.
• 모델러에서 의사 결정자로 이어지는 커뮤니케이션 강화(예: 권장 사항을 보다 신뢰할 수 있고, 이해할 수 있으며, 설득력이 있거나 설득력이 있는 것으로 함).
• 모델 출력이 최대 또는 최소이거나 최적 기준을 충족하는 입력 요소의 공간에서 영역 찾기(최적화 및 몬테카를로 필터링 참조).
• 파라미터 수가 많은 모델을 보정하는 경우 1차 민감도 테스트를 통해 민감한 파라미터에 초점을 맞추어 보정 단계를 용이하게 할 수 있습니다.매개 변수의 민감도를 알지 못하면 민감하지 않은 ^[2]매개 변수에 쓸데없이 시간을 소비할 수 있습니다.
• 관측치, 모형 입력, 예측 또는 예측 간의 중요한 연결 관계를 파악하여 더 나은 ^[3][4]모형을 개발하는 데 도움이 됩니다.

개요

수학적 모델(예: 생물학, 기후 변화, 경제학 또는 공학)은 매우 복잡할 수 있으며, 그 결과 입력과 출력 사이의 관계가 잘 이해되지 않을 수 있습니다.이러한 경우 모델은 블랙박스로 볼 수 있습니다. 즉, 출력은 입력의 "불투명한" 함수입니다.모델 입력의 일부 또는 전부는 측정 오류, 정보 부재, 구동력 및 메커니즘에 대한 불충분한 또는 부분적인 이해 등 불확실성의 원인이 되는 경우가 많습니다.이러한 불확실성은 모델의 반응 또는 출력에 대한 우리의 신뢰에 제한을 가합니다.또한, 모델은 확률적 ^[5]사건의 발생과 같은 시스템의 자연적인 내재적 변동성에 대처해야 할 수도 있습니다.

많은 입력 변수가 포함된 모형에서 민감도 분석은 모형 구축 및 품질 보증의 필수 요소입니다.영향 평가 연구와 관련된 국내 및 국제 기관은 지침에 민감도 분석에 전념하는 섹션을 포함했습니다.예를 들어, 유럽 위원회(영향 ^[6]평가 지침 참조), 백악관 관리 및 예산국, 기후 변화에 관한 정부간 패널 및 미국 환경 보호국의 모델링 ^[7]지침 등이 있습니다.

설정, 제약 조건 및 관련 문제

설정 및 제약 조건

민감도 분석 방법의 선택은 일반적으로 여러 가지 문제 제약 조건 또는 설정에 따라 결정됩니다.가장 일반적인 것들입니다.

• 계산 비용:민감도 분석은 거의 항상 모형 a(아마도 많을 수도 있음)번 실행함으로써 수행됩니다. 즉, 샘플링 기반 ^[8]접근법입니다.이것은 중대한 문제가 될 수 있습니다.
  • 모형을 한 번 실행할 때 상당한 시간(분, 시간 이상)이 걸립니다.이는 매우 복잡한 모델에서는 드문 일이 아닙니다.
  • 모형에 불확실한 입력이 많습니다.민감도 분석은 기본적으로 다차원적인 입력 공간을 탐색하는 것으로, 입력의 수에 따라 기하급수적으로 크기가 증가합니다.차원성의 저주를 보십시오.

계산 비용은 많은 실제 민감도 분석에서 문제가 됩니다.계산 비용을 절감하는 몇 가지 방법에는 에뮬레이터(대형 모델의 경우)의 사용, 스크리닝(문제의 차원성을 줄이기 위한) 방법 등이 있습니다.또 다른 방법은 시간이 제한된 ^[9]응용 프로그램의 변수 선택을 위해 이벤트 기반 민감도 분석 방법을 사용하는 것입니다.이는 시스템 입력 및 출력의 변화의 흔적에 대한 정보를 민감도 분석을 사용하여 조합하여 이벤트를 트리거하는 원인으로서 입력 데이터와 다음을 설명하는 출력 데이터 사이의 관계를 매핑하도록 설계된 입력/출력 트리거/이벤트 행렬을 생성하는 입력 변수 선택(IVS) 방법입니다.실제 사건상태 변화의 원인, 즉 입력 변수와 효과 시스템 출력 매개 변수 간의 인과 관계는 어떤 입력 집합이 주어진 출력에 실제적인 영향을 미치는지를 결정합니다.이 방법은 최소의 계산 ^[9][10]오버헤드로 가능한 가장 짧은 시간에 시스템 상태 변화를 이해하고 해석하려고 하기 때문에 해석 및 계산 IVS 방법에 비해 분명한 장점이 있습니다.

• 상관 입력:대부분의 일반적인 민감도 분석 방법은 모형 입력 간의 독립성을 가정하지만 때로는 입력이 강한 상관 관계를 가질 수도 있습니다.이것은 아직 미성숙한 연구 분야이고 확정적인 방법은 아직 확립되지 않았습니다.
• 비선형성:선형 회귀를 기반으로 하는 것과 같은 일부 민감도 분석 접근법은 모형 반응이 입력에 대해 비선형적인 경우 민감도를 부정확하게 측정할 수 있습니다.이러한 경우 분산 기반 측도가 더 적합합니다.
• 다중 출력:사실상 모든 민감도 분석 방법은 단일 일변량 모형 출력을 고려하지만, 많은 모형이 공간적으로 또는 시간에 따라 많은 수의 데이터를 출력합니다.각 관심 출력에 대해 다른 민감도 분석을 수행할 가능성이 배제되는 것은 아닙니다.그러나 출력이 상관 관계에 있는 모형의 경우 민감도 측도를 해석하기 어려울 수 있습니다.

가정 대 추론

불확실성 및 민감도 분석에서는 분석가가 입력 가정을 탐색하는 데 얼마나 신중한지와 그에 따른 추론의 폭 사이에 결정적인 균형이 있습니다.그 점은 계량경제학자 에드워드 E에 의해 잘 설명되고 있습니다. 리머:^[11][12]

저는 대안 가정의 이웃을 선택하고 그에 상응하는 추론의 간격을 파악하는 '글로벌 민감도 분석'이라고 부르는 조직화된 민감도 분석의 형태를 제안했습니다.가정의 주변이 신뢰할 수 있을 정도로 넓고 해당 추론 간격이 유용할 정도로 좁은 경우에만 결론이 견고하다고 판단됩니다.

참고 Leamer는 가정의 선택에서 '신뢰성'의 필요성을 강조합니다.모델을 무효화하는 가장 쉬운 방법은 모델이 가정의 불확실성과 관련하여 취약하다는 것을 증명하거나 모델의 가정이 충분히 '넓게' 받아들여지지 않았다는 것을 보여주는 것입니다.제롬 R. 라베츠(Jerome R. Ravetz)도 동일한 개념을 표현하는데, 이는 입력의 불확실성을 억제하여 출력이 ^[13]결정되지 않도록 해야 할 때를 의미합니다.

함정과 어려움

민감도 분석에서 몇 가지 일반적인 어려움은 다음과 같습니다.

• 분석할 모델 입력이 너무 많습니다.스크리닝을 사용하여 치수를 줄일 수 있습니다.차원성의 저주에 대처하는 또 다른 방법은 낮은 불일치^[14] 시퀀스에 기초한 샘플링을 사용하는 것입니다.
• 모델을 실행하는 데 시간이 너무 오래 걸립니다.에뮬레이터(HDMR 포함)는 모델을 가속화하거나 필요한 모델 실행 횟수를 줄임으로써 전체 시간을 줄일 수 있습니다.
• 입력에 대한 확률 분포를 구축하기에 충분한 정보가 없습니다.확률 분포는 전문가의 도출을 통해 구성할 수 있지만, 그 경우에도 신뢰할 수 있는 분포를 구축하는 것은 어려울 수 있습니다.확률 분포 또는 범위의 주관성은 민감도 분석에 강력한 영향을 미칩니다.
• 분석 목적이 불분명합니다.다른 통계적 검정과 측도가 문제에 적용되고 다른 요인 순위가 획득됩니다.테스트는 대신 분석의 목적에 맞게 조정되어야 합니다. 예를 들어 어떤 요인이 높은/낮은 값의 출력을 생성하는데 가장 큰 책임이 있는지 관심이 있는 경우 몬테카를로 필터링을 사용합니다.
• 너무 많은 모형 출력이 고려됩니다.이는 하위 모델의 품질 보증에는 허용될 수 있지만 전체 분석 결과를 제시할 때는 피해야 합니다.
• 조각 단위의 민감도.이것은 한 번에 하나의 하위 모델에 대해 민감도 분석을 수행하는 경우입니다.이 접근 방식은 여러 하위 모델의 요인들 간의 상호 작용을 간과할 수 있기 때문에 보수적이지 않습니다(유형 II 오류).

민감도 분석법

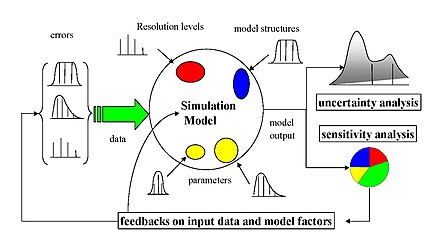
민감도 분석을 수행하기 위한 많은 접근법이 있으며, 이 중 많은 접근법은 위에서 논의한 제약 조건 중 하나 이상을 해결하기 위해 개발되었습니다.또한 분산 분해, 부분 도함수 또는 기본 효과를 기반으로 한 민감도 측정 유형에 따라 구분됩니다.그러나 일반적으로 대부분의 절차는 다음과 같은 개요를 따릅니다.

1. 각 입력(예: 범위, 확률 분포)의 불확실성을 정량화합니다.이것은 어려울 수 있으며 주관적인 ^[15]데이터로부터 불확실성 분포를 이끌어내기 위한 많은 방법들이 존재합니다.
2. 분석할 모델 출력을 식별합니다(관심 대상은 이상적으로 모델이 다루는 문제와 직접적인 관계가 있어야 함).
3. 선택 방법과 입력 불확도에 따라 결정되는 일부 ^[16]실험 설계를 사용하여 모형을 여러 번 실행합니다.
4. 결과 모형 출력을 사용하여 관심 있는 민감도 측도를 계산합니다.

예를 들어 사용자가 전체 감도 분석을 수행하기 전에 중요하지 않은 변수를 걸러내야 하는 고차원 문제에서 이 절차가 반복되는 경우도 있습니다.

다양한 유형의 "핵심 방법"(아래에서 설명)은 계산되는 다양한 민감도 측정에 의해 구별됩니다.이 범주들은 어떻게든 겹칠 수 있습니다.문제의 제약 조건 하에서 이러한 측정치를 얻을 수 있는 대안적인 방법이 제시될 수 있습니다.

한 번에 하나씩(OAT)

가장 단순하고 일반적인 접근 방식 중 하나는 단일 요인(OAT)을 변경하여 출력에 어떤 영향을 ^[17][18][19]미치는지 확인하는 것입니다.OAT는 일반적으로 다음을 포함합니다.

• 하나의 입력 변수를 이동하고, 다른 입력 변수들은 기준치(기준치) 값을 유지한 다음,
• 변수를 공칭 값으로 되돌린 다음 다른 입력 각각에 대해 동일한 방식으로 반복합니다.

그런 다음 부분 도함수 또는 선형 회귀와 같은 출력의 변화를 모니터링하여 감도를 측정할 수 있습니다.출력에서 관찰되는 모든 변화는 변경된 단일 변수로 인한 것이므로 논리적인 접근 방식으로 나타납니다.또한 한 번에 하나의 변수를 변경하여 다른 모든 변수를 중앙값 또는 기준선 값으로 고정할 수 있습니다.이렇게 하면 결과의 비교 가능성이 높아지고(모든 '효과'는 동일한 공간의 중심점을 기준으로 계산됨) 여러 입력 요소가 동시에 변경될 때 컴퓨터 프로그램이 충돌할 가능성을 최소화할 수 있습니다.OAT는 실용적인 이유 때문에 모델러들이 자주 선호합니다.OAT 분석 하에서 모델 고장의 경우 모델러는 어떤 것이 고장의 원인이 되는 입력 요소인지 즉시 알 수 있습니다.

그러나 이 접근법은 단순함에도 불구하고 입력 변수의 동시 변화를 고려하지 않기 때문에 입력 공간을 완전히 탐색하지는 못합니다.이는 OAT 접근법이 입력 변수 간의 상호작용을 감지할 수 없으며 비선형 모형에 적합하지 ^[20]않음을 의미합니다.

OAT 접근 방식으로 탐색되지 않은 상태로 남아 있는 입력 공간의 비율은 입력의 수에 따라 기하급수적으로 증가합니다.예를 들어, 한 번에 하나씩 탐색되는 3변수 매개변수 공간은 원점에 중심을 둔 정육면체의 x, y, z 축을 따라 점을 찍는 것과 같습니다.이 모든 점을 경계하는 볼록 선체는 전체 매개변수 공간의 1/6만 부피를 갖는 팔면체입니다.일반적으로, 초직각의 축들의 볼록한 선체는 부피${\displaystyle 분율}$이 1$/$n!{\$displaystyle 1/$n$!\}$인 초팔면체를 형성합니다. 5개의 입력으로 탐색된 공간은 이미 전체 매개변수 공간의 1% 미만으로 떨어집니다.그리고 축외 볼륨은 실제로 샘플링되지 않고 있기 때문에 이마저도 과대평가입니다.이를 공간의 무작위 표본 추출과 비교해 보면, 볼록한 선체는 점이 ^[21]더 많아질수록 전체 부피에 근접합니다.OAT의 희소성은 이론적으로 선형 모델에 대한 관심이 아니지만, 진정한 선형성은 자연에서 거의 없습니다.

도함수 기반 국소법

국소 도함수 기반 방법은 입력_i 인자 X에 대해 출력 Y의 부분 도함수를 취하는 것을 수반합니다.

${\displaystyle \left {\frac {\partial Y}{\partial X_{i}}\right _{\textbf {x}}^{0}}}$

여기서 첨자⁰ x는 도함수가 입력 공간의 어떤 고정된 점에서 취해진다는 것을 나타냅니다(클래스의 이름으로 '로컬'이라고 함).이^[22][23] 클래스의 방법은^[24] 인접 모델링(Adjoint modeling)과 자동 미분(Automated Differentiation)입니다.OAT와 유사하게 로컬 방법은 일반적으로 한 번에 하나의 변수인 작은 섭동을 검사하기 때문에 입력 공간을 완전히 탐색하려고 시도하지 않습니다.Neural Networks를 통해 파생 기반 민감도에서 유사한 샘플을 선별하고 불확도 정량화를 수행할 수 있습니다.

로컬 방법의 장점 중 하나는 시스템의 모든 민감도를 나타내는 행렬을 만들 수 있다는 것입니다. 따라서 많은 수의 입력 및 출력 변수가 있는 경우 글로벌 방법으로는 달성할 수 없는 개요를 제공합니다.

^[25]

회귀분석

회귀 분석은 민감도 분석의 맥락에서 선형 회귀 분석을 모형 반응에 적합시키고 표준화된 회귀 계수를 민감도의 직접적인 측정으로 사용하는 것을 포함합니다.회귀 분석은 표준화된 계수를 해석하기 어렵기 때문에 데이터에 대해 선형이어야 합니다(즉, 2차 항이 없는 초평면 등).따라서 이 방법은 모형 반응이 실제로 선형일 때 가장 적합하며, 예를 들어 결정 계수가 큰 경우 선형성을 확인할 수 있습니다.회귀분석의 장점은 단순하고 계산 비용이 적게 든다는 것입니다.

분산 기반 방법

분산 기반^[26] 방법은 입력 및 출력 불확실성을 확률 분포로 정량화하고 출력 분산을 입력 변수와 변수 조합에 기인한 부분으로 분해하는 확률론적 접근 방법의 한 종류입니다.따라서 입력 변수에 대한 출력의 민감도는 해당 입력으로 인해 발생하는 출력의 변화량으로 측정됩니다.이들은 조건부 기대치, 즉 X = {X, X, ...X}에 대한 모델 Y = f(X)를 고려할 때 i번째 변수 X의 민감도 척도는 다음과 같이 주어집니다.

${\displaystyle \operatorname {Var} \left(E_{\textbf {X}}_{\simi}}\left(Y\mid X_{i}\right)\right)}$

여기서 "Var"와 "E"는 각각 분산 및 기댓값 연산자를 나타내고_~i, X는 X를 제외한_i 모든 입력 변수의 집합을 나타냅니다.이 식은 기본적으로 Y의 불확실성(분산)에 대한 기여도 X만을_i 측정하며(다른 변수의 변동에 비해 평균화됨) 1차 민감도 지수 또는 주효과 지수로 알려져 있습니다.중요한 것은 다른 변수와의 교호작용으로 인한 불확실성을 측정하지 않는다는 것입니다.총 효과 지수로 알려진 추가 측도는 X로 인해_i 발생하는 Y의 총 분산과 다른 입력 변수와의 교호작용을 제공합니다.두 양은 일반적으로 Var(Y)로 나누어 표준화됩니다.

분산 기반 방법을 사용하면 입력 공간의 완전한 탐색, 교호작용 및 비선형 반응을 계산할 수 있습니다.이러한 이유로 계산이 가능할 때 널리 사용됩니다.일반적으로 이 계산에는 몬테카를로 방법이 포함되지만, 수천 개의 모델 실행이 포함될 수 있기 때문에 필요할 때 다른 방법(에뮬레이터 등)을 사용하여 계산 비용을 절감할 수 있습니다.

반응 표면(VARS)의 Variogram 분석

이전 민감도 분석 방법의 주요 단점 중 하나는 매개변수 공간에서 모델 Y=f(X)의 응답 표면/출력의 공간적으로 순서화된 구조를 고려하지 않는다는 것입니다.방향성 베리오그램과 공보그램의 개념을 활용하여 반응 표면(VARS)의 베리오그램 분석은 Y 값에 공간적으로 연속적인 상관 구조를 인식하고, ${\displaystyle \frac{\mathrm{따라서}}{}}$∂ Y ∂ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{i_{}}{}}${\$partial$ Y$}{\partial x_{i$의 값에도 적용함으로써 이러한 약점을 해결합니다.

기본적으로 변동성이 높을수록 특정 섭동 척도에서 특정 방향/모수를 따라 반응 표면이 이질적입니다.따라서 VARS 프레임워크에서, 주어진 섭동 척도에 대한 방향성 베리오그램의 값은 방향성 및 섭동 척도 개념 모두에 대한 베리오그램 분석을 연결함으로써 민감도 정보의 포괄적인 설명으로 고려될 수 있습니다.결과적으로 VARS 프레임워크는 민감도가 척도 의존적 개념이라는 사실을 설명하여 전통적인 민감도 분석 ^[29]방법의 척도 문제를 극복합니다.더 중요한 것은, VARS가 다른 전략보다 훨씬 낮은 계산 비용으로 비교적 안정적이고 통계적으로 강력한 매개 변수 민감도 추정치를 제공할 수 있다는 점입니다(약 2배 ^[30]더 효율적임).주목할 만한 점은 VARs 프레임워크와 분산 기반 및 파생 기반 접근 방식 사이에 이론적 연결이 있다는 것입니다.

대체방법

위에서 논의한 제약 조건 중 일부를 극복하기 위해 여러 가지 방법이 개발되었으며, 그렇지 않으면 민감도 측정치의 추정이 불가능해집니다(대부분 계산 비용으로 인해).일반적으로 이러한 방법은 분산 기반 민감도 측정치를 효율적으로 계산하는 데 중점을 둡니다.

에뮬레이터

에뮬레이터(메타 모델, 대리 모델 또는 응답 표면이라고도 함)는 모델 ^[31]자체의 입력/출력 동작을 근사화하는 에뮬레이터로 알려진 비교적 간단한 수학적 기능을 구축하는 것을 수반하는 데이터 모델링/기계 학습 접근 방식입니다.즉, '모델링(modeling a modeling)'의 개념(따라서 메타모델(metamodel)이라는 이름)입니다.이 아이디어는 컴퓨터 모델이 해결하는 데 오랜 시간이 걸릴 수 있는 매우 복잡한 일련의 방정식일 수 있지만 항상 입력 Y = f(X)의 함수로 간주될 수 있다는 것입니다.입력 공간의 여러 점에서 모델을 실행하면 θ(X) θ f(X)가 허용 가능한 ^[32]오차 범위 내에 있도록 훨씬 간단한 에뮬레이터 θ(X)를 맞출 수 있습니다.그러면 (몬테카를로 또는 해석적으로) 에뮬레이터로부터 감도 측정값을 계산할 수 있으며, 이는 무시할 수 있는 추가 계산 비용을 갖게 됩니다.중요한 것은 에뮬레이터를 적합시키는 데 필요한 모델 런의 수가 ^[33]모델에서 민감도 측도를 직접 추정하는 데 필요한 런의 수보다 작을 수 있다는 점입니다.

에뮬레이터 접근법의 핵심은 모델 f에 충분히 근접한 근사치인 θ(에뮬레이터)를 찾는 것입니다.이를 위해서는 다음과 같은 단계가 필요합니다.

1. 모형의 입력 공간에 있는 여러 점에서 표본을 추출(실행)합니다.이를 위해서는 샘플 설계가 필요합니다.
2. 사용할 에뮬레이터 유형(수학적 함수) 선택
3. 모델의 샘플 데이터를 사용하여 에뮬레이터를 "교육"합니다. 일반적으로 에뮬레이터가 실제 모델을 최대한 모방할 때까지 에뮬레이터 매개 변수를 조정합니다.

모델의 샘플링은 수학자 일리야 M에 의해 소볼 수 있는 것과 같이 낮은 불일치 시퀀스로 수행될 수 있습니다. 소볼(Sobol) 또는 라틴어 하이퍼큐브 샘플링(Latin hypercube sampling), 비록 임의의 설계도 사용될 수 있지만, 어느 정도의 효율성을 잃게 됩니다.교육 방법은 에뮬레이터의 종류에 따라 달라지기 때문에 에뮬레이터 종류의 선택과 교육은 본질적으로 연결되어 있습니다.민감도 분석에 성공적으로 사용된 일부 유형의 에뮬레이터는 다음을 포함합니다.

• 출력 점의 임의 조합이 다변량 가우스 분포로 가정되는 가우스^[33] 프로세스(크리깅이라고도 함).최근에는 이질적이고 불연속적인 ^[34][35]반응을 처리하기 위해 "나무" 가우스 프로세스가 사용되고 있습니다.
• 다수의 의사결정 나무가 훈련되고 결과가 평균화되는 랜덤 포레스트.^[31]
• 그라디언트 ^[31]부스팅(gradient boosting): 일련의 단순 회귀를 사용하여 데이터 점에 가중치를 부여하여 오류를 순차적으로 줄입니다.
• 직교 다항식을 사용하여 반응 표면을 근사화하는 다항식 혼돈 ^[36]확장입니다.
• 일반적으로 HDMR 잘라내기와 함께 사용되는 스무딩 스플라인(^[37]smoothing spline)(아래 참조).
• 이산 베이지안 ^[38]네트워크는 잡음 모델과 같은 표준 모델과 함께 사용됩니다.잡음 모델은 변수 사이의 조건부 독립성에 대한 정보를 이용하여 차원성을 크게 줄입니다.

에뮬레이터를 사용하면 기계 학습 문제가 발생하는데, 이는 모델의 반응이 비선형적인 경우 어려울 수 있습니다.모든 경우 에뮬레이터의 정확도를 확인하는 데 유용합니다. 예를 들어 교차 검증을 사용합니다.

고차원 모델 표현(HDMR)

고차원 모델 표현(HDMR)(^[39][40]항은 H. Rabitz에^[41] 기인함)은 본질적으로 에뮬레이터 접근 방식이며, 함수 출력을 입력 항과 증가하는 차원의 상호 작용의 선형 조합으로 분해하는 것을 포함합니다.HDMR 접근 방식은 일반적으로 고차 상호 작용(2차 또는 3차 이상)을 무시함으로써 모델이 잘 근사화될 수 있다는 사실을 이용합니다.절단된 영상 시리즈의 항은 각각 다항식 또는 스플라인(REFS)과 절단 순서까지의 주효과 및 교호작용의 합으로 표현되는 반응으로 근사화될 수 있습니다.이러한 관점에서 볼 때, HDMR은 고차 상호 작용을 무시하는 에뮬레이터로 볼 수 있습니다. 장점은 전차 에뮬레이터보다 더 높은 차원을 가진 모델을 에뮬레이트할 수 있다는 것입니다.

푸리에 진폭 민감도 테스트(FAST)

FAST(Fourier Amplitude Sensitivity Test)는 푸리에 영상 시리즈를 사용하여 단일 주파수 변수를 사용하여 주파수 영역의 다변량 함수(모델)를 나타냅니다.따라서 민감도 지수를 계산하는 데 필요한 적분값이 일변량이 되어 계산 비용이 절감됩니다.

다른.

몬테카를로 ^[42]필터링을 기반으로 하는 방법들.<이들은 샘플링 기반이기도 하며, 여기서 목적은 출력의 특정 값(예: 높음 또는 낮음)에 해당하는 입력 인자의 공간 내 영역을 식별하는 것입니다.

적용들

민감도 분석의 예는 다음과 같은 다양한 응용 분야에서 찾아볼 수 있습니다.

• 환경과학
• 비지니스
• 사회과학
• 화학
• 공학 기술
• 역학
• 메타분석
• 다기준 의사결정
• 시간적으로 중요한 의사결정
• 모형교정
• 불확도 정량화
• 카오스 이론
  • 모집단 유전학 - 확률^{[43]: 183} 기간을 받았을 때 모집단이 혼돈 상태에 빠질지 여부

민감도 감사

모델 기반 연구의 민감도 분석은 추론을 뒷받침하고, 추론이 정책 또는 의사 결정 과정에 투입되는 상황에서 견고성을 증명하기 위한 것일 수 있습니다.이러한 경우 분석 자체의 틀, 제도적 맥락, 저자의 동기 등이 매우 중요한 문제가 될 수 있으며, 모수적 불확실성에 중점을 둔 순수한 민감도 분석은 불충분하다고 볼 수 있습니다.프레이밍에 대한 강조는 정책연구의 관련성으로부터 서로 다른 규범과 가치를 특징으로 하는 다양한 선거구에 대한 지역간의 관계를 이끌어낼 수 있으며, 따라서 '무엇이 문제인가'에 대한 다른 이야기, 그리고 무엇보다도 '누가 이야기를 하고 있는가'에 대한 다른 이야기를 이끌어낼 수 있습니다.프레이밍에는 대부분 다소 암묵적인 가정이 포함되며, 이는 기술(예: 상수로 취급될 수 있는 변수)에 이르기까지 정치적(예: 보호해야 하는 그룹)일 수 있습니다.

이러한 우려를 충분히 고려하기 위해 SA의 도구는 전체 지식 및 모델 생성 과정에 대한 평가를 제공하도록 확장되었습니다.이러한 접근 방식을 '감도 감사'라고 부릅니다.이것은 숫자의 '^[44]Pedigrees' 생성과 함께 정량적 정보의 가치를 평가하는 데 사용되는 방법인 NUSAP에서 영감을 얻었습니다.민감도 감사는 특히 적대적 맥락을 위해 설계되었으며, 여기서 증거의 성격뿐만 아니라 증거와 관련된 확실성과 불확실성의 정도가 당파적 ^[45]이익의 대상이 될 것입니다.민감도 감사는 유럽 ^[46]아카데미의 정책을 위한 과학적 조언 보고서 뿐만 아니라 영향 ^[6]평가를 위한 유럽 집행위원회 지침에서 권장됩니다.

관련개념

민감도 분석은 불확실성 분석과 밀접한 관련이 있습니다. 후자는 연구 결론의 전반적인 불확실성을 연구하는 반면, 민감도 분석은 어떤 불확실성의 원천이 연구 결론에 더 큰 영향을 미치는지 확인하려고 합니다.

민감도 분석에서의 문제 설정은 ^[47]실험의 설계 분야와도 강한 유사성을 가지고 있습니다.실험의 설계에서, 어떤 과정이나 개입('치료')이 어떤 대상('실험 단위')에 미치는 영향을 연구합니다.민감도 분석에서는 수학적 모델의 입력이 모델 자체의 출력에 미치는 영향을 확인합니다.두 분야 모두에서 최소한의 물리적 또는 수치적 실험을 통해 시스템으로부터 정보를 얻기 위해 노력합니다.

참고 항목

참고문헌

추가열람

• Cannavó, F. (2012). "Sensitivity analysis for volcanic source modeling quality assessment and model selection". Computers & Geosciences. 44: 52–59. Bibcode:2012CG.....44...52C. doi:10.1016/j.cageo.2012.03.008.
• Fassò A. (2007) "통계적 민감도 분석과 수질"Wymer L. Ed, 수질 기준 및 모니터링을 위한 통계 프레임워크.와일리, 뉴욕.
• Fassò A., Perri P.F. (2002) "민감성 분석"Abdel H. El-Shaarawi와 Walter W. Piegorsch (eds) 환경측정학 백과사전, 4권, 1968-1982, Wiley.
• Fassò A., Esposito E., Porcu E., Reverberi A.P., Vegliò F.(2003) "오염 폐수에 대한 충전식 기둥 반응기의 통계적 민감도 분석"환경 측정.Vol. 14, n.8, 743–759.
• 하우그, 에드워드 J.;최경K; Komkov, Vadim (1986) 구조시스템의 설계민감도 분석Mathematics in Science and Engineering, 177. Academic Press, Inc., Orlando, FL.
• Pianosi, F.; Beven, K.; Freer, J.; Hall, J.W.; Rougier, J.; Stephenson, D.B.; Wagener, T. (2016). "Sensitivity analysis of environmental models: A systematic review with practical workflow". Environmental Modelling & Software. 79: 214–232. doi:10.1016/j.envsoft.2016.02.008.
• Pilkey, O.H. and L. Pilkey-Jarvis (2007), 쓸모없는 산술. 환경 과학자들이 미래를 예측하지 못하는 이유.뉴욕: 컬럼비아 대학 출판부.
• Santner, T.J.; Williams, B.J.; Notz, W.I. (2003) 컴퓨터 실험의 설계와 분석; Springer-Verlag.
• 탈렙, N. N. N., (2007) 흑조: 불가능성이 높은 랜덤 하우스의 영향.

외부 링크

• SAMO 컨퍼런스 시리즈 자료를 이용한 웹사이트 (1995-2025)
• 민감도 분석 웹 페이지 – (유럽연합 집행위원회 공동 연구 센터)
• 공동연구센터 글로벌 민감도 분석 무료 소프트웨어 심랩
• MUCM Project Archived 2013-04-24 at the Wayback Machine – 계산 수요가 많은 모델의 불확실성 및 민감도 분석을 위한 광범위한 리소스