가우스 과정

확률 이론과 통계에서 가우스 공정은 확률적 공정(시간이나 공간에 의해 지수화된 무작위 변수의 집합)으로, 그러한 변수의 모든 유한한 집합은 다변량 정규 분포를 가지며, 즉 이들 변수의 모든 유한한 선형 조합이 정상적으로 분포한다. 가우스 공정의 분포는 모든 (무한히 많은) 무작위 변수의 공동 분포로서, 이와 같이 시간이나 공간과 같은 연속적인 영역을 갖는 함수에 대한 분포다.

가우스 공정의 개념은 가우스 분포(정상 분포)의 개념에 기초하기 때문에 칼 프리드리히 가우스(Carl Friedrich Gauss)의 이름을 따서 명명된다. 가우스 과정은 다변량 정규 분포의 무한 차원 일반화로 볼 수 있다.

가우스 프로세스는 통계적 모델링에 유용하며, 정규 분포로부터 물려받은 속성에서 이익을 얻는다. 예를 들어, 무작위 공정을 가우스 공정으로 모델링하는 경우, 다양한 파생 수량의 분포를 명시적으로 얻을 수 있다. 그러한 수량은 시간의 범위에 걸친 공정의 평균값과 적은 시간 집합에서 표본 값을 사용하여 평균을 추정하는 오류를 포함한다. 정확한 모형은 데이터 양이 증가함에 따라 잘 확장되지 않는 경우가 많지만, 정확한 정확도를 유지하면서 계산 시간을 대폭 단축하는 여러 가지 근사법이 개발되었다.

정의

시간 연속 확률 프로세스${\displaystyle }${${\displaystyle X{}_{}}$ ${\displaystyle t_{}}$ t${\displaystyle t}$ ${\displaystyle T}$} ${\$\${\displaystyle {}_{}}$ $T\right\}}$은(는) 색인 $집합{\displaystyle }$ T ${\\displaystytle t_$${1},\ldots, t_{k$$}$의 모든 유한 집합에 대해 가우스인 경우만 해당된다.

${\displaystyle \mathbf {X} _{t_{1},\ldots,t_{k}=(X_{t_{1},\ldots,X_{t_{k})}}$

다변량 가우스 랜덤 변수.^[1] 그것은${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle {t{}_{}}_{}}$ ${\displaystyle {{1\mathrm{}}_{}}_{}}$,${\displaystyle }$… ,${\displaystyle }$X ${\displaystyle {t_{}}_{}}$ $){\displaystyle (X_{t_{1},\ldots ,X_{t_{k}}})$의 모든 선형 조합이 일변량 정규 분포(또는 가우스 분포)를 가지고$$ 있다고 말하는 것과 같다.

Using characteristic functions of random variables, the Gaussian property can be formulated as follows: ${\displaystyle \left\{X_{t};t\in T\right\}}$ is Gaussian if and only if, for every finite set of indices ${\displaystyle t_{1},\ldots ,t_{k}}$, there are real-valued ${\dis$$playstyle \sigma _{\ell j}}$, ${\displaystyle \mu _{\ell }}$ with ${\displaystyle \sigma _{jj}>0}$ such that the following equality holds for all ${\displaystyle s_{1},s_{2},\ldots ,s_{k}\in \mathbb {R} }$

${\displaystyle \operatorname {E} \left(\exp \left(i\ \sum _{\ell =1}^{k}s_{\ell }\ \mathbf {X} _{t_{\ell }}\right)\right)=\exp \left(-{\frac {1}{2}}\,\sum _{\ell ,j}\sigma _{\ell$$j}s_{\ell }s_{j}+i\sum _{\ell }\mu _{\ell s_{\ell$ }s_{\ell $}\right)}$.

여기서 $i{\displaystyle }$ ${\displaystyle i}$은(는) ${\displaystyle {i\mathrm{}}^{}}$ ${\displaystyle 2{}^{}}$=${\displaystyle }$- 1 ${\displaystyle i^{2}=-1}$과(와) 같은 가상 단위를 의미한다$.$

$\sigma {\displaystyle {}_{}}$ ${\displaystyle {\ell }_{}}$ j ${\$${\ell j}$ 및 ${\displaystyle {\mu }_{}}$ μ ${\$은(는) 그 과정에서 변수의 공분산 및 수단임을 나타낼 수 있다$$.^[2]

분산

가우스 공정의 분산은 형식적으로^{[3]: p. 515} $언제$든지 t ${\displaystyle t}$에서 유한하다$.$

${\displaystyle \operatorname {var} [X(t)]=\operatorname {E} [ X(t)-\operatorname {E} [X(t)] ^{2}]<\infty \quad {\text{for all }}t\in T}$.

역학성

일반적인 확률적 과정의 경우 엄격한 감각의 역소성은 넓은 감각의 역소성을 내포하지만 모든 넓은 감각의 정지 상태에서의 확률적 과정이 엄격한 감각의 정지 상태를 의미하는 것은 아니다. 그러나 가우스 확률적 과정의 경우 두 개념은 동등하다.^{[3]: p. 518}

가우스 확률적 과정은 만약 넓은 감각의 정지 상태라면 엄격한 감각의 정지 상태를 말한다.

예

정지해 있는 가우스 과정에 대한 명시적 표현이 있다.^[4] 이 표현의 간단한 예는 다음과 같다.

${\displaystyle X_{t}=\cos(at)\xi _{1}+\sin(at)\xi _{2}$

여기서 $\xi {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$및$$ ${\displaystyle {\xi \mathrm{}}_{}}$ 2 ${\$}}은 표준 정규 분포를 따르는 독립 랜덤 변수다$$.

공분산 함수

가우스 과정의 핵심 사실은 2차 통계로 완전히 정의할 수 있다는 것이다.^[5] 따라서 가우스 공정이 평균 0을 갖는다고 가정할 경우 공분산 함수를 정의하면 공정의 행동이 완전히 정의된다. 중요한 것은 이 함수의 비음극적 명확성은 카루넨-로브 확장을 이용한 스펙트럼 분해를 가능하게 한다는 점이다. 공분산 함수를 통해 정의할 수 있는 기본적인 측면은 공정의 역점성, 동위원소성, 부드러움 및 주기성이다.^[6][7]

측점성(Stationparity)은 두 점 x ${\displaystyle$ $x$$}$과 $x{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$ x$'}$의 분리에 관한 공정의 행동을 가리킨다$.$ 공정이 정지되어 있으면 ${\displaystyle {}^{}}$의 분리에 따라 x${\displaystyle }$- x ${\displaystyle {\prime }^{}}$ ${\$}에 따라 달라지는 반면$,$ 역점${\displaystyle }$x {\$displaysty$}의 실제 위치에 따라 달라진다.le $x}$과 $x{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$ x$\text{'}\}.$ 예를 들어, Ornstein–의 특수한 경우.브라운 운동 과정인 Uhlenbeck 과정은 정지되어 있다.

공정이 ${\displaystyle x}$- ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ $displaystyle x-x' }$, $x{\displaystyle }$ ${\displaystyle$ x$}$과 $x{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$ 사이의 유클리드 거리(방향은 아님$)$에만 의존하면 공정이 등방성으로 간주된다. 동시에 정지해 있고 등방성이 있는 공정은 균질하다고 간주된다.^[8] 실제로 이러한 특성은 관찰자의 위치가 주어진 공정 행동의 차이(또는 오히려 그러한 특성들의 결여)를 반영한다.

궁극적으로 가우스 프로세스는 함수에 대한 프리저를 취하는 것으로 해석되며, 이러한 프리러의 부드러움은 공분산 함수에 의해 유도될 수 있다.^[6] 만일 우리가 "근접" 입력 지점 $x{\displaystyle }$ ${\displaystyle$ x$}$ 및 $x$ ′ ${\$ x$'}$의 출력 지점 $y{\displaystyle }$ ${\displaystyle$ $y$$}$과 $y{\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$ y$'}$도 "근접"이$$ 될 것으로 예상한다면 연속성의 가정이 존재한다. 만약 우리가 상당한 변위를 허용하고 싶다면, 우리는 더 거친 공분산 함수를 선택할 수 있을 것이다. 극단적인 행동의 예는 오른슈타인-이다.Uhlenbeck 공분산 함수와 전자는 절대 다를 수 없고 후자는 무한히 다를 수 있는 제곱 지수함수.

주기성은 프로세스의 행동 내에서 주기적인 패턴을 유도하는 것을 말한다. 형식적으로 입력 $x{\displaystyle }$ ${\displaystyle x}$을(를) 2차원 벡터 $u{\displaystyle (}$ x${\displaystyle }$)${\displaystyle }$=${\displaystyle }$(${\displaystyle \cos }$ ${\displaystyle }$( ${\displaystyle x}$)${\displaystyle }$, ${\displaystyle \sin }$ ${\displaystyle }$( ${\displaystyle x}$)${\$)(x$)=\좌측(\cos($x),\$sin($x)\$right)}$에 매핑함으로써 달성된다$.$

일반적인 공분산 함수

공통 공분산 함수는 다음과 같다.^[7]

• 상수 : $K{\displaystyle {}_{}}$ ${\displaystyle C{}_{}}$ x${\displaystyle }$, ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$)${\displaystyle }$= ${\displaystyle C}$ ${\displaystyle K_{\operatorname {C}}}(x,x')=$$C}$
• 선형: $K{\displaystyle {}_{}}$ ${\displaystyle {L\mathrm{}}_{}x}$, ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$)${\displaystyle }$= ${\displaystyle {}^{}}$ T ${\displaystyle {}^{}{}^{}}$ ${\displaystyle {\prime }^{}}$ ${\$$T}x'}$
• 백색 가우스 소음: $K{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{GN}}_{}{}^{},}$ x ${\displaystyle {\prime }^{}}$)${\displaystyle }$= ${\displaystyle {{}^{}}_{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle x_{}}$, x ${\displaystyle {{\prime }^{}}_{}}$ ${\$2}\$delta _{x,x$'}}}}}}}}}=\sigma ^{$2}\$delta _x,x,x,x,x,x$'}}}}$
• 제곱 지수: $K{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{SE}}_{}x,}$ ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$)${\displaystyle }$= ${\displaystyle \exp }$ ${\displaystyle }$(${\displaystyle }$- ${\displaystyle \frac{{}^{\mathrm{}}}{}}$ ${\displaystyle \frac{{}^{}}{\mathrm{}}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}^{}}{}}$) ${\$
• 올슈타인-Uhlenbeck: $K{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{OU}}_{}}$(${\displaystyle {}^{}}$, x ${\displaystyle {\prime }^{}}$)${\displaystyle }$= ${\displaystyle \exp }$ ${\displaystyle }$(${\displaystyle }$- d ${\displaystyle \frac{\ell }{}}$) ${\$
• Matérn: ${\displaystyle K_{\operatorname {Matern} }(x,x')={\frac {2^{1-\nu }}{\Gamma (\nu )}}{\Big (}{\frac {{\sqrt {2\nu }} d }{\ell }}{\Big )}^{\nu }K_{\nu }{\Big (}{\frac {{\sqrt {2\nu }} d }{\ell$$}}}{\Big )}}}}}$
• Periodic: ${\displaystyle K_{\operatorname {P} }(x,x')=\exp \left(-{\frac {2\sin ^{2}\left({\frac {d}{2}}\right)}{\ell ^{2}}}\right)}$
• 합리적 이차: $K{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{RQ}}_{}\mathrm{x},}$ x ${\displaystyle {\prime }^{}}$)${\displaystyle }$= (${\displaystyle }$1${\displaystyle }$+ ${\displaystyle {}^{\mathrm{}}}$ 2${\displaystyle {}^{}{}^{}}$) -${\displaystyle {\alpha }^{}}$ ${\displaystyle \alpha }$, α, α, α, ${\displaystyle \mathrm{\alpha }}$, ${\displaystyle \ge }$ 0 ${\daystyle K_{\\operatorname {RQ}}(x,x')=(1+d$^{2$})^{-\alpha },\qua \geq 0}$

여기서 $d{\displaystyle }$= ${\displaystyle x}$ -${\displaystyle {}^{}}$ $′$ ${\$ 매개 변수 $\ell {\displaystyle }$ ${\displaystyle \ell }$은(는) 공정의 특성 길이 척도$$(실제로 두 점 $x{\displaystyle }${\$displaysty x}$와 x${\displaystyle {}^{}}${$${\$displaystyty x}$이 서로 유의하게 영향을 미치려면$$ 얼마나 근접해야 함) $\Delta {\displaystyle }$ ${\\\delta$Δ가$$ 크론커다. $델타{\displaystyle }$ 및 ▼ ${\displaystyle \sigma}$ 소음 변동의 표준 편차. 더욱이 $K{\displaystyle {}_{}}$ ${\$은 $순서{\displaystyle }$bes {\$displaystyle \nu }$의 변형된 베셀 함수,$$ ($displaystyle \$$Gamma$ $(\nu )$는 $\nu$ ${\displaystysty$\comparique$$\carique \carique }}에서 평가된 공분산 함수를 선형 조합으로 정의할 수 있다$.$ace는 현재 데이터 세트에 대한 다른 통찰력을 통합하기 위해 기능한다.

분명히, 추정 결과는 모델의 동작을 정의하는 하이퍼 파라미터 ${\displaystyle \theta}($예$$: $\ell {\displaystyle }$ ${\displaystyle \ell }$ 및 $\sigma {\displaystyle }$ ${\displaystyle \sigma$$})$의 값에 따라 달라진다. $\theta {\displaystyle }$ ${\displaystyle \theta }$에 대해 일반적으로 선택되는 선택은 이전에 선택한 것과 함께 최대 후미(MAP) 추정치를 제공하는 것이다$$. 전자가 거의 균일하다면 이는 공정의 한계우도를 최대화하는 것과 같다. 관측된 $공정{\displaystyle }$ 값 y ${\displaystyle y}$에 대해 한계화가 수행된다$.$^[7] 이 접근방식은 최대우도 II, 증거 최대화 또는 경험적 베이지라고도 한다.^[9]

연속성

가우스 공정의 경우 확률의 연속성은 평균 제곱 연속성과 동일하며, 확률 1의 연속성은 표본 연속성과 동일하다.^{[11]: 91 "Gaussian processes are discontinuous at fixed points."} 후자는 확률상 연속성을 암시하지만 암시하지는 않는다. 확률의 연속성은 평균과 자기 분산도가 연속 함수인 경우에만 유지된다. 이와는 대조적으로 샘플 연속성은 정지된 가우스 프로세스(안드레이 콜모고로프에서 처음 언급했을 가능성이 높은 것처럼)에서도 어려웠고 보다 일반적인 프로세스에서도 더 어려웠다.^{[12]: Sect. 2.8 [13]: 69, 81 [14]: 80 [15]} 통상적으로, 샘플 연속 공정은 샘플 연속 수정을 인정하는 프로세스를 의미한다. ^{[16]: 292 [17]: 424}

고정 케이스

정지 가우스 $프로세스{\displaystyle }$ X${\displaystyle }$=${\displaystyle }$( ${\displaystyle {}_{}}$ ${\displaystyle t_{}{}_{}}$) ${\displaystyle t_{}}$ ${\displaystyle {\in }_{}}$ ${\displaystyle {R\mathbb{}}_{}}$, ${\displaystyle$ X$=(X_{t})_{t\in \mathb {R}}}}$의 경우 스펙트럼의 일부$$ 조건은 샘플 연속성에 충분하지만 필요하지 않다. 때로는 Dudley-Fernique 정리라고 불리는 필요하고도 충분한 조건은$by{\displaystyle }$ {\$displaystyle \sigma }$에 의해 정의된$$ 기능을 포함한다.

${\displaystyle \sigma (h)={\sqrt {\mathb {E} {\big (}X(t+h)-X(t){\big )}^{2}}$

(우측 측면은 역점성으로 인해$$ $t{\displaystyle }$ ${\displaystyle t}$에 의존하지 않음). $확률상$ X$${\$displaystyle$$$X}의 연속성은 ${\displaystyle \mathrm{at<img\; alt="\backslash sigma\; "\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/59f59b7c3e6fdb1d0365a494b81fb9a696138c36"\; style="vertical-align:\; -0.338ex;\; width:1.33ex;\; height:1.676ex;"\; papago-attr-id="264">}}$ {\$displaystyle \$$sigma$ $}$의 연속성 0${\displaystyle \mathrm{.}}$ ${\displaystyle$ 0$.}$ ${\$$displaystyle$ $\$$ma$$(h)$와 $($$h{\displaystyle }$→$$으로$)$의 합성이 너무 느릴 때$$ $X$의 샘플 연속성인 경우$,$ X {\$displaysty$ of X styty of X는 같다.${}$이(가) 실패할 수 있음$$. 다음과 같은 통합의 융합이 중요하다.

${\displaystyle I(\sigma )=\int _{0}^{1}{{0}^{{0}{\sqrt{\log(1/h)}}}}}}\,dh=\int _{0}^{0}^{\2}\sigma (\mathb {e}{-x^{}}}},dx)\x)\dx,},},},}$

these two integrals being equal according to integration by substitution ${\displaystyle h=\mathbb {e} ^{-x^{2}},}$ ${\displaystyle \textstyle x={\sqrt {\log(1/h)}}.}$ The first integrand need not be bounded as ${\displaystyle h\to 0+,}$ thus the integral may converge ( ( ) ${\displaystyle I(\sigma )<\infit$ 또는 divage (${\displaystyle }$ (${\displaystyle \sigma }$)${\displaystyle }$= ${\displaystyle \mathrm{\infty }}$ ${\displaystyle$ I$(\sigma )=\inft }.$ Taking for example ${\displaystyle \sigma (\mathbb {e} ^{-x^{2}})={\tfrac {1}{x^{a}}}}$ for large ${\displaystyle x,}$ that is, ${\displaystyle \sigma (h)=(\log(1/h))^{-a/2}}$ for small ${\displaystyle h,}$ one obtains )<>∞{\displaystyle I(\sigma)<, \infty}때 a>1,{\displaystyle a>, 1,}과 나는(σ))∞{I(\sigma)=\infty\displaystyle} 때 0<>;≤ 1. 기능 σ{\displaystyle \sigma}[0, ∞),{-LSB- 0,\infty)\displaystyle,}에 증가하는 이 두 경우{0<, a\leq 1\displaystyle.}지만.일반적으로 n은게다가, 조건도

${\displaystyle }$(${\displaystyle \ast }$ ) ${\displaystyle (*)}$에는 > {\$displaystyle$$$\$varepsilon >0}$이(가) 존재하므로 $[{\displaystyle }$ ${\displaystyle$ \$varipsilon$ }}은$($는) [ ${\displaystyle 0,}$ ${\displaystyle \epsilon }$ ${\displaystyle ]}$ ${\displaystylean$ [0$,\bylon ]$에 모노톤 ]이다$$.

$\sigma {\displaystyle }$ ${\displaystyle \sigma }$과(와) ${\displaystyle \mathrm{\sigma }}$( h${\displaystyle }$)$$ ( ) ${\displaystyle 0}$ {\$displaystyle \sigma (h)\geq 0}($모든 $h{\displaystyle }$ ${\displaysty h$ 및 $\sigma {\displaystyle }$(${\displaystyle 0}$) = ${\displaystyle 0.}$ ${\displaystystystyle \sigma (0)=$0)=0)의 연속성으로부터 따르지 않는다$.$$}$

정리 1. $\sigma {\displaystyle }$ ${\displaystyle \sigma }$을(를) 연속적으로$$ 하고 (${\displaystyle \ast }$)${\displaystyle }$. ${\displaystyle(*)$을 만족시키도록 한다.$}$ ${\$$displaystyle I(\sigma){\sigma}$ 조건$$ I$({\$$displaystyle X.}$의 $샘플{\displaystyle }$ 연속성을 위해 필요하고 충분하다.

어떤 역사.^{[17]: 424} 1964년 자비에 페르니크가 수완을 발표했지만 최초의 증거는 리처드 M에 의해 발표되었다. 1967년 ^{[16]: Theorem 7.1} 더들리 필요성은 Michael B에 의해 증명되었다. 1970년 마커스와 로렌스 셉.^{[18]: 380}

$샘플{\displaystyle }$ 연속 공정 $X{\displaystyle }$ ${\displaystyle X}$이(가) 존재하며, I$$${\displaystyle }$( ${\displaystyle \sigma }$)${\displaystyle }$= ${\displaystyle \infty ;}$ ${\displaystyle$ I$(\sigma )=\infit;}$은(는) 조건${\displaystyle (\ast }$)을 위반한다${\displaystyle .}$ ${\displaystyty*).$$}}$ 마커스와 셰프가 발견한 예는$$ 무작위 라쿠나리 푸리에 시리즈다.

${\displaystyle X_{t}=\sum _{n=1}^{\inful }c_{n}(\xi _{n}\cos \lambda _{n}t+\eta _{n}\sin \lambda _{n}t),}$

표준 정규 분포와 함께 있습니다 ξ 1, η 1, ξ 2, η 2, 달려가서{\displaystyle \xi_{1},\eta _{1},\xi _{2},\eta _{2},\dots}은 독립 확률 변수, 주파수 0개체, λ 1<>λ 2<쭉 펼쳐져{\displaystyle 0<, \lambda_{1}<, \lambda _{2}<, \dots}이 급성장하는 시퀀스와 계수. cn>0{\di.Splaystyle c_{n}>0};∞∑ 소음 한계 n<>를 충족해야 한다.{\displaystyle\textstyle \sum_{n}c_{n}<, \infty.}그 후자는 관계를 암시하 E∑ 소음 한계 n(ξ n+η n))∑ 소음 한계에 대해 E(ξ n+η n))const ⋅∑ 소음 한계 n<>∞,{\displaystyle\textstyle \mathbb{E}.\sum _{n}c_{n}(\xi_{n}+\eta_{n})=\sum _{n}c_{n}\mathbb{E}(\xi_{n}+\eta_{n})={\text{const}}\cdot\sum _{n}c_{n}<, \infty,}(Wordsworth).∑ 소음 한계 n(ξ n+η n)<>∞{\displaystyle \sum_{n}(\xi_{n}+\eta_{n})<, \infty}거의 확실히, 푸리에 시리즈의 평등 수렴 거의 s을 보장한다urely$d{\displaystyle }$ X${\displaystyle }$. ${\displaystyle$ X$.}$의 샘플 연속성

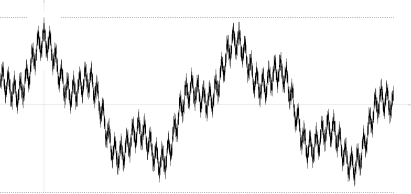
그것의 자기공포함수

${\displaystyle \mathbb {E}X_{t+h}=\sum _{n=1}^{n=1}{n1}^{\infit }c_{n}^{2}\cos \lambda _{n}h}$

해당 함수 $\sigma {\displaystyle }$, ${\displaystyle \chostma ,}$은(는) not monotone(사진 참조)이 아니다.

${\displaystyle \sigma (h)={\sqrt {2\mathbb {E} X_{t}X_{t}-2\mathbb {E} X_{t}X_{t+h}}}=2{\sqrt {\sum _{n=1}^{\infty }c_{n}^{2}\sin ^{2}{\frac {\lambda _{n}h}{2}}}}.}$

가우스 과정의 필수 요소로서의 브라운 운동

위너 공정(Brownian motion)은 백색 잡음이 일반화된 가우스 공정의 정수다. 고정된 것은 아니지만, 고정된 증가가 있다.

올슈타인-Uhlenbeck 공정은 정지된 가우스 공정이다.

브라운 다리는 (오른슈타인처럼)Uhlenbeck 공정) 증분이 독립적이지 않은 가우스 공정의 예.

소수 브라운 운동은 가우스 과정으로 공분산 함수가 위너 프로세스의 공분산 함수를 일반화한다.

드리스콜의 제로원 법칙

드리스콜의 제로원 법칙은 가우스 공정에 의해 생성된 샘플 함수의 특징을 나타내는 결과물이다.

Let ${\displaystyle f}$ be a mean-zero Gaussian process ${\displaystyle \left\{X_{t};t\in T\right\}}$ with non-negative definite covariance function ${\displaystyle K}$. Let ${\displaystyle {\mathcal {H}}(R)}$ be a Reproducing kernel Hilbert space with positive definite kernel ${\displaystyle R}$$(\backslash$$displaystyle R)$

그러면

→ [ - 1 < ${\displaystyle \lim$_{$n\to \inft }\operatorname {tr}[K_{n}R_{n}^{n$}-1$}]<\infty$

여기서 ${\displaystyle {Kn}_{}}$ ${\$ 및$$ ${\displaystyle {Rn}_{}}$ ${\$은 $n{\displaystyle }$ ${\displaystyle$ n$} 포인트$의 가능한$$ 모든 쌍의 공분산 행렬이다$$.

${\displaystyle \mathrm{Pr}}$[ ${\displaystyle f}$ ${\displaystyle \in }$ ${\displaystyle H}$( R${\displaystyle }$) ${\displaystyle ]}$= 1 ${\displaystyle \Pr[f\in {\mathcal {H}(R)]=1$

게다가

${\displaystyle \lim _{n\to \flotty }\operatorname {tr}[K_{n}R_{n}^{-1}]=\flotty }}$

함축적으로 말하다

${\displaystyle Pr}$[ ${\displaystyle f\mathcal{}}$ ${\displaystyle \in }$ H${\displaystyle }$( ${\displaystyle R}$) ${\displaystyle ]}$= ${\displaystyle 0}$ ${\displaystyle \Pr[f\in {\mathcal {H}(R)]=0}$^[19].

$이$는 K${\displaystyle }$= ${\displaystyle R}$ ${\displaystyle K=R}$이$($가) 다음과 같은 경우에 중요한 의미를 갖는다.

${\displaystyle \lim _{n\to \infty }\operatorname {tr} [R_{n}R_{n}^{-1}]=\lim _{n\to \infty }\operatorname {tr} [I]=\lim _{n\to \infty }n=\infty }$.

이와 같이, 양의 확정 $커널{\displaystyle }$ K ${\displaystyle K}$을(를) 가진 평균 영 가우스 공정의 거의 모든 샘플 경로는 힐버트 $공간{\displaystyle \mathcal{}}$ H${\displaystyle }$( K $){\displaystyle {\mathcal{H}(K)$ 밖에 위치하게 된다$$$.$

선형 제약 가우스 공정

많은 관심분야의 응용분야에서는 현재 시스템에 대한 기존의 지식이 이미 제공되어 있다. 예를 들어 가우스 공정의 출력이 자기장에 해당하는 경우를 생각해 보십시오. 여기서, 실제 자기장은 맥스웰 방정식으로 구속되며, 이 제약조건을 가우스 공정 형식주의에 통합하는 방법은 알고리즘의 정확성을 향상시킬 가능성이 높기 때문에 바람직할 것이다.

가우스 프로세스에 선형 제약 조건을 통합하는 방법은 이미 존재한다.^[20]

선형 제약 조건을 따르는 것으로 알려진$$ (벡터 값) 출력 $함수{\displaystyle }$ f ${\displaystyle (x}$) ${\displaystyle f(x)}$을(를) 고려하십시오(${\displaystyle {예}_{}}$:$$F X {\$displaystyle {\\mathcal {F}_$${X}).$

${\displaystyle {\mathcal{F}_{X}(f(x)=0).}$

Then the constraint ${\displaystyle {\mathcal {F}}_{X}}$ can be fulfilled by choosing ${\displaystyle f(x)={\mathcal {G}}_{X}(g(x))}$, where ${\displaystyle g(x)\sim {\mathcal {GP}}(\mu _{g},K_{g})}$ is modelled as a Gaussian process, and finding ${\displaystyle {\mathcal{G}}_{}}$ ${\displaystyle X_{}}$ ${\$s$$.t.

${\displaystyle {\mathcal {F}_{X}({\mathcal {G}_{X}(g)=0\qquad \forall g.}$

$G{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle X_{}}$ ${\$을(를) 부여하고$$ 가우스 공정이 선형 변환에 따라 닫힌다는 사실을 $이용$하여 F$${\$displaystyle f}$ $제약조건{\displaystyle {\mathcal{}}_{}}$ F ${\displaystyle X_{}}${\$displaystyle${\$mathcal}{X}$에 대한 가우스 공정이 된다$$.

${\displaystyle f(x)={\mathcal {G}_{X}g\sim {\mathcal {G}_{X}\matcal {G}\mathcal {G}{X}K_{\mathcal {G}{G}}{X'}^{T}}$

따라서 선형 제약조건은 가우스 공정의 평균 및 공분산 함수로 인코딩될 수 있다.

적용들

가우스 프로세스는 베이시안 추론에서 함수에 대한 사전 확률 분포로 사용될 수 있다.^[7][22] 함수의 원하는 영역에 N점 세트가 있으면 공분산 행렬 매개 변수가 원하는 커널을 가진 N점의 Gram 행렬인 다변량 가우시안(Gaussian)을 취하여 해당 가우시안으로부터 표본을 추출하십시오. 다중 출력 예측 문제의 해결을 위해 벡터 값 함수에 대한 가우스 공정 회귀 분석이 개발되었다. 이 방법에서는 '큰' 공분산이 생성되는데, 원하는 도메인의 N 포인트에서 취해진 모든 입력과 출력 변수 사이의 상관관계를 설명한다.^[23] 이 접근방식은 매트릭스 값 가우스 프로세스에 대해 상세하게 설명되었고 학생-t 프로세스와 같이 '꼬리가 더 무거운' 프로세스를 가진 프로세스로 일반화되었다.^[24]

가우스 공정 이전의 연속 값 추론을 가우스 공정 회귀(Gaussian process regression) 또는 크라이징(Kriging)이라고 하며, 가우스 공정 회귀(Gaussian process regression)를 다중 표적 변수로 확장하는 것을 코크리깅(cokriging)이라고 한다.^[25] 따라서 가우스 프로세스는 강력한 비선형 다변량 보간 도구로서 유용하다.

또한 가우스 프로세스는 확률론적 숫자 분야에서 수치적 통합, 미분 방정식 해결 또는 최적화와 같은 수치적 분석 문제를 다루기 위해 일반적으로 사용된다.

가우스 프로세스는 예를 들어 전문가 모델이 혼합된 맥락에서 사용될 수 있다.^[26][27] 그러한 학습 프레임워크의 근본적인 논리는 주어진 매핑이 단일 가우스 프로세스 모델에 의해 잘 포착될 수 없다는 가정에 있다. 대신 관측 공간은 하위 집합으로 나뉘는데, 각 하위 집합은 서로 다른 매핑 함수로 특징지어지며, 이들 각각은 가정된 혼합물의 다른 가우스 프로세스 구성요소를 통해 학습된다.

가우스 공정 예측 또는 Kriging

일반적인 가우스 공정 회귀 문제(Kriging)와 관련된 경우, $좌표{\displaystyle }$ x ${\displaystyle x}$에서 관측된$$ 가우스 $공정{\displaystyle }$ f ${\$$displaystyle$ f$}$의 경우$,$ $f{\displaystyle (x}$ ${\displaystyle )}$값 벡터($x)$는 치수의 다변량 가우스 분포에서 추출한 표본의 수에 불과하다고$$ 가정한다. $관측{\displaystyle }$ 좌표 n ${\displaystyle n$ Therefore, under the assumption of a zero-mean distribution, ${\displaystyle f(x')\sim N(0,K(\theta ,x,x'))}$, where ${\displaystyle K(\theta ,x,x')}$ is the covariance matrix between all possible pairs ${\displaystyle (x,x')}$ for a given set of hyperp아라미터 ^[7]θ 로그 한계 가능성은 다음과 같다.

${\displaystyle \log p(f(x')\mid \theta ,x)=-{\frac {1}{2}}f(x)^{T}K(\theta ,x,x')^{-1}f(x')-{\frac {1}{2}}\log \det(K(\theta ,x,x'))-{\frac {n}{2}}\log 2\pi }$

그리고 θ에 대한 이러한 한계우도를 최대화하는 것은 가우스 공정 f의 완전한 사양을 제공한다. 이 시점에서 첫 번째 항은 모형이 관측치를 적합시키지 못함에 따른 벌칙 항에 해당하고 두 번째 항은 모형의 복잡성에 비례하여 증가하는 벌칙 항에 해당한다는 것을 간단히 알 수 있다. Having specified θ, making predictions about unobserved values ${\displaystyle f(x^{*})}$ at coordinates x* is then only a matter of drawing samples from the predictive distribution ${\displaystyle p(y^{*}\mid x^{*},f(x),x)=$$N(y^{*}\mid A,B)}($후측$$ 평균 추정치 A가 다음과 같이 정의됨)

${\displaystyle A=K(\theta,x^{*}x)K(\theta,x,x')^{-1}f(x)}$

그리고 후분산 추정치 B는 다음과 같이 정의된다.

${\displaystyle B=K(\theta,x^{*},x^{*})-K(\theta,x^{*},x)^{-1}K(\theta,x^{*}x)^{\theta,x)^{{*}}}^{{}}}T}$

where ${\displaystyle K(\theta ,x^{*},x)}$ is the covariance between the new coordinate of estimation x* and all other observed coordinates x for a given hyperparameter vector θ, ${\displaystyle K(\theta ,x,x')}$ and ${\displaystyle f(x)}$ are defined as before and ${\displaystyle K(\theta ,x^{}}$${\displaystyle {\ast }^{}}$, ${\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$) ${\displaystyle K(\theta ,x^{*},x^{*}}}$는 θ에서 지시하는 대로 x* 지점에서의 분산이다$$. 사실상 후측 평균 $추정치{\displaystyle }$ f${\displaystyle ({}^{}}$ )$${\$displaystyle$f($x^{*})}("$점 추정치")는 $관측치{\displaystyle }$ f${\displaystyle (x}$ )$${\$displaystyle$ f$(x)}$의 선형 조합일 $뿐$이며$,$ 이와 유사한 방식으로 f( ${\displaystyle {}^{}(}$ )$${\$displaystystyle$ f$($x^{*})의 분산은 관측치와 실제로 독립적이다$$.ons $f{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle$ f$(x$ 가우스 프로세스 예측에서 알려진 병목현상은 추론과 우도 평가의 계산 복잡성이 x의 숫자에 입방체라는 것이며, 따라서 더 큰 데이터 집합에 대해 실현 불가능해질 수 있다는 것이다.^[6] 희박한 가우스 프로세스에 대한 작업으로, 대개 주어진 공정 f에 대한 대표 세트를 구축한다는 생각에 기초하여, 이 문제를 회피하려고 노력한다.^[28][29] 크라이깅 방법은 공간 기능 예측을 위해 비선형 혼합 효과 모델의 잠재 수준에 사용할 수 있다. 이 기법을 잠적 크라이깅이라고 한다.^[30]

Often, the covariance has the form ${\displaystyle K(\theta ,x,x')={\frac {1}{\sigma ^{2}}}{\tilde {K}}(\theta ,x,x')}$, where ${\displaystyle \sigma ^{2}}$ is a scaling parameter. 예를 들어 Matérn 클래스 공분산 함수를 들 수 있다. If this scaling parameter ${\displaystyle \sigma ^{2}}$ is either known or unknown (i.e. must be marginalized), then the posterior probability, ${\displaystyle p(\theta \mid D)}$, i.e. the probability for the hyperparameters ${\displaystyle \theta }$ given a set of data pairs ${\displaystyle D}$ of o$x{\displaystyle }$ ${\displaystyle x}$ 및$$ $f{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle f(x)}$의 관측은 분석 표현을 허용한다$.$^[31]

가우스 과정으로서의 베이지안 신경망

베이시안 신경망은 딥러닝과 인공신경망 모델을 확률적으로 처리하고, 그 매개변수에 사전 분포를 할당하는 데서 비롯되는 베이시안 네트워크의 특정한 유형이다. 인공신경망에서의 연산은 대개 인공신경세포의 순차적 층으로 구성된다. 한 층에 있는 뉴런의 수는 층 폭이라고 불린다. 레이어 폭이 커짐에 따라 많은 베이시안 신경망은 폐쇄형 합성 커널을 가진 가우스 과정으로 감소한다. 이 가우스 과정은 NNGP(Neural Network Gaussian Process)라고 불린다.^[7][32][33] 베이지안 신경망으로부터의 예측을 보다 효율적으로 평가할 수 있게 하고, 딥러닝 모델을 이해할 수 있는 분석 도구를 제공한다.

계산 문제

실제 적용에서 가우스 공정 모델은 다변량 정규 분포를 유도하는 격자에서 평가되는 경우가 많다. 최대우도를 사용한 예측 또는 모수 추정에 이러한 모형을 사용하려면 다변량 가우스 밀도를 평가해야 하며, 여기에는 공분산 행렬의 결정요인과 역행렬의 계산이 포함된다. 이 두 작업 모두 입방체 계산 복잡성을 가지고 있어 그리드의 크기가 작더라도 두 작업 모두 엄청난 계산 비용을 가질 수 있다. 이러한 단점은 여러 가지 근사 방법을 개발하도록 이끌었다.

참고 항목

• 베이즈 선형 통계량
• 베이시안적 정규화 해석
• 크리깅
• 가우스 자유장
• 가우스-마코프 프로세스
• GEK(Gradient-enhanced Kriging)
• 학생의 t-과정

참조

외부 링크

• 라스무센과 윌리엄스의 기계 학습을 위한 가우스 프로세스 웹 사이트
• 가우스 프로세스에 대한 완만한 소개
• 가우스 랜덤 필드 및 상관 함수 검토
• 가우스 공정을 이용한 효율적인 보강 학습

소프트웨어

• GPML: GP 회귀 분석 및 분류를 위한 종합 Matlab 도구 상자
• STK: Kriging 및 GP 모델링을 위한 소형(Matlab/Octave) 툴박스
• UQLab 프레임워크의 Kriging 모듈(Matlab)
• 고정 가우스 필드의 Matlab/Octave 기능
• Yelp MOE – 가우스 프로세스 학습을 사용하는 블랙박스 최적화 엔진
• OODACE – 유연한 객체 지향 Kriging Matlab 도구 상자.
• GPstuff – Matlab 및 옥타브용 가우스 공정 도구 상자
• GPy – Python의 가우스 프로세스 프레임워크
• GSTOols - Python으로 작성된 가우스 공정 회귀 분석을 포함한 정지 상태 도구 상자
• 대화형 가우스 프로세스 회귀 데모
• C++11로 작성된 기본 가우스 프로세스 라이브러리
• Scikit-learn – 가우스 프로세스 회귀 분석 및 분류를 포함하는 Python용 기계 학습 라이브러리
• [1] - Kriging ToolKit (KriKit)은 Forschungszentrum Jülich (FZJ)의 생물학 및 지질학 연구소 (IBG-1)에서 개발되었다.

비디오 튜토리얼

• David MacKay의 가우스 프로세스 기본 사항
• 칼 에드워드 라스무센의 가우스 과정과 함께 배우기
• 칼 에드워드 라스무센의 베이시안 추론과 가우스 과정