슈테른-게를라흐 실험

에 대한 일련의 기사의 일부
양자역학
${\displaystyle i\hbar {\frac {\partial }{\partial t}} \psi(t)\rangle ={\hat {H} \psi(t)\rangle }$ 슈뢰딩거 방정식
서론 용어집 역사
배경 고전역학 구양자론 브라켓 표기법 해밀토니안 방해다
펀더멘털 상보성 디코히어런스 얽힘 에너지 준위 측정. 비국소성 양자수 주 중첩 대칭성 터널링 불확실성 파동함수 쓰러짐
실험 벨의 부등식 다비송-독일 더블슬릿 Elitzur–Vaidman 프랭크-헤르츠 레게트 – 가르기 등식 마하젠더 포퍼 양자지우개 지연선택 슈뢰딩거의 고양이 슈테른-게를라흐 휠러의 지연 선택
제형 개요 하이젠베르크 상호작용 매트릭스 위상공간 슈뢰딩거 이력 합계(경로 적분)
방정식 디랙 클라인고든 파울리 뤼드베르크 슈뢰딩거
해석 베이지안 일관 이력 코펜하겐 드브로이-봄 앙상블 숨은 변수 현지의 초결정론 다세계 대물붕괴 양자논리학 관계형 거래적 폰 노이만-비그너
고급주제 상대론적 양자역학 양자장이론 양자정보과학 양자전산 양자 혼돈 EPR 역설 밀도행렬 산란설 양자통계역학 양자기계학습
사이언티스트 아하로노프 벨 베테 블래킷 블로흐 봄 보어 태어난 보스 드브로이 콤프턴 디랙 데이비슨 데비 에렌페스트 아인슈타인 에버렛 포크 페르미 파인만 글라우버 구츠윌러 하이젠베르크 힐베르트 조던 크라머르스 파울리 새끼 양 란다우 라우에 모즐리 밀리칸 온네스 플랑크 라비 라만 뤼드베르크 슈뢰딩거 시몬스 소머펠트 폰 노이만 웨일 빈 위그너 지만 자일링거
v t

양자 물리학에서 스턴-게를라흐 실험은 각운동량의 공간 방향이 양자화됨을 보여주었습니다. 따라서 원자 규모의 시스템은 본질적으로 양자적 특성을 가지고 있는 것으로 나타났습니다. 원래 실험에서 은 원자는 공간적으로 변하는 자기장을 통해 보내졌고, 이 자기장은 유리 슬라이드와 같은 검출기 스크린에 닿기 전에 굴절되었습니다. 자기장 구배 때문에 자기 모멘트가 0이 아닌 입자는 직선 경로에서 편향되었습니다. 화면에는 양자화된 스핀으로 인해 연속적인 분포가 아닌 이산적인 축적 지점이 나타났습니다.^[1] 역사적으로 이 실험은 모든 원자 규모 시스템에서 각운동량 양자화의 현실을 물리학자들에게 설득하는 데 결정적이었습니다.^[2][3][4]

1921년 오토 스턴(Otto Stern)에 의해 구상된 후, 이 실험은 1922년 초 발터 제를라흐(Walther Gerlach)와 함께 처음으로 성공적으로 수행되었습니다.^[1][5][6]

묘사

스턴-게를라흐 실험은 은 원자들을 불균일한 자기장을 통해 보내고 그들의 편향을 관찰하는 것을 포함합니다.

결과는 입자가 고전적으로 회전하는 물체의 각운동량과 매우 유사한 고유 각운동량을 가지고 있지만 특정 양자화된 값만 가지고 있음을 보여줍니다. 또 다른 중요한 결과는 입자의 스핀 중 한 가지 성분만 한 번에 측정할 수 있다는 것인데, 이는 z축을 따라 스핀을 측정하면 x축과 y축을 따라 입자의 스핀에 대한 정보가 파괴된다는 것을 의미합니다.

실험은 일반적으로 은 원자와 같은 전기적으로 중성인 입자를 사용하여 진행됩니다. 이것은 자기장을 통해 이동하는 하전 입자 경로의 큰 편향을 피하고 스핀 의존적인 효과가 지배할 수 있도록 합니다.^[7][8]

입자를 고전적인 회전 자기 쌍극자로 취급할 경우 자기장이 쌍극자에 작용하는 토크 때문에 자기장에서 세차 운동을 하게 됩니다(토크 유도 세차 참조). 균질한 자기장을 통해 이동하면 쌍극자의 양 끝에 작용하는 힘이 서로 상쇄되어 입자의 궤적은 영향을 받지 않습니다. 그러나 자기장이 균일하지 않을 경우 쌍극자의 한쪽 끝에 작용하는 힘은 반대쪽 끝에 작용하는 힘보다 약간 더 커지므로 입자의 궤적을 편향시키는 알짜 힘이 존재합니다. 입자가 고전적인 회전 물체라면 스핀 각운동량 벡터의 분포가 무작위적이고 연속적일 것으로 예상할 수 있습니다. 각 입자는 외부 필드 구배와 함께 자기 모멘트의 도트 곱에 비례하는 양만큼 편향되어 디텍터 화면에 약간의 밀도 분포를 생성합니다. 대신에, 스턴-게를라흐 장치를 통과하는 입자들은 특정한 양만큼 위 또는 아래로 편향됩니다. 이것은 현재 스핀 각운동량으로 알려진 양자 관측 가능량을 측정한 것으로 관측 가능한 값 또는 점 스펙트럼의 이산 집합을 갖는 측정의 가능한 결과를 보여주었습니다.

원자 스펙트럼과 같은 일부 이산 양자 현상은 훨씬 이전에 관찰되었지만, 스턴-게를라흐 실험을 통해 과학자들은 과학 역사상 처음으로 이산 양자 상태 간의 분리를 직접 관찰할 수 있었습니다.

이론적으로 어떤 종류의 양자 각운동량에도 이산 스펙트럼이 있으며, 이 스펙트럼은 때때로 "각운동량은 양자화된다"고 짧게 표현됩니다.

+를 가진 입자를 이용한 실험1⁄2 or −1⁄2 spin

전자처럼 대전된 입자를 이용해 실험을 진행하면 궤도를 둥글게 휘는 경향이 있는 로렌츠 힘이 발생합니다. 이 힘은 하전 입자의 경로를 가로지르는 적절한 크기의 전기장에 의해 취소될 수 있습니다.

전자는 스핀-1 ⁄2 입자입니다. 이들은 어떤 축을 따라 측정된 두 가지 가능한 스핀 각운동량 값,$$+$$ℏ 2 ${\displaystyle +{\frac {\hbar$}{${\displaystyle 2}\}\}$ ${\displaystyle \frac{\mathrm{또는}}{}}$- ℏ 2${\displaystyle -{\frac${\hbar}{2}}, 순수 양자역학 현상입니다. 값이 항상 같기 때문에 전자의 고유한 특성으로 간주되며, 때때로 "내성 각운동량"(다른 입자의 존재에 따라 달라질 수 있으며 궤도 각운동량과 구별하기 위해)이라고도 합니다. 수직 축을 따라 스핀을 측정하면 전자는 각각 위 또는 아래를 가리키는 자기 모멘트를 기준으로 "위로" 또는 "아래로"라고 설명됩니다.

스핀${\displaystyle }$+ ${\displaystyle \frac{12}{}}$ ${\$ 입자$$ 실험을 수학적으로 설명하려면 디랙의 브라켓 표기법을 사용하는 것이 가장 쉽습니다. 입자가 Stern-Gerlach 장치를 통과할 때 입자는 위쪽 또는 아래쪽으로 편향되며, 감지기에 의해 관찰되어 위로 회전하거나 아래로 회전합니다. $이$ 값은 ${\displaystyle \frac{\mathrm{각운동량}}{}}$ 양자 번호$$j ${\$$displaystyle$ j$}$로 설명되며$,$ +$$ℏ 2 {\$displaystyle$+{\$frac {\$hbar$}}$ ${\displaystyle \frac{\mathrm{또는}}{}}$ - ℏ 2 ${\displaystyle$-$frac$ {\hbar}{2}} 중 하나를 사용할 수 있습니다. $z{\displaystyle }$ ${\displaystyle z}$ 축을$$ 따라 운동량을 관찰(측정)하는 행위는 연산자 ${\displaystyle {Jz}_{}}$ ${\$에 해당합니다$.$^[specify] 수학적 용어로 설명하자면 입자의 초기 상태는

${\displaystyle \psi \rangle = c_{1}\left \psi _{j=+{\frac {\hbar}{2}}\right\rangle +c_{2}\left \psi _{j=-{\frac {\hbar}{2}}\right\rangle }$

여기서 상수 $c{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ 및 ${\displaystyle c_{}}$ 2 ${\$는 복소수입니다. 이 초기 상태 스핀은 모든 방향을 가리킬 수 있습니다. The squares of the absolute values ${\displaystyle c_{1} ^{2}}$ and ${\displaystyle c_{2} ^{2}}$ determine the probabilities that for a system in the initial state ${\displaystyle \psi \rangle }$ one of the two possible values of ${\displaystyle j}$ is found after 측정이 이루어 졌습니다. 상수 $c$ ${\displaystyle 1_{}}$ ${\displaystyle c_{1}}$ 및 ${\displaystyle c_{}}$ $2$ ${\displaystyle c_{2}}$도 하나의 값을 찾을 확률이 일치하도록 정규화되어야 합니다. 즉, ${\displaystyle c{}^{}}$ + ${\displaystyle {}^{}}$ ${\displaystyle {22}_{}}$ =${\displaystyle 1}${\displaystyle c_{1} ^{2}+ c_{2} ^{2}=1} 이 되도록 해야 합니다. 그러나, 이 정보는 복소수이기 때문에 $c{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}${\$displaystyle c_{$1$$}} ${\displaystyle {및\mathrm{}}_{}}$ c$$2 {\$displaystyle c_{$2}}의 값을 결정하기에는 충분하지 않습니다$.$ 따라서 측정 결과 상수의 제곱 크기만 산출되며, 이 값은 확률로 해석됩니다.

순차 실험

여러 Stern-Gerlach 장치(S-G를 포함하는 직사각형)를 연결하면 단순한 선택기 역할을 하지 않는다는 것을 분명히 알 수 있습니다. 즉, (측정에 존재하는) 상태 중 하나로 입자를 필터링하고 다른 상태를 차단하는 것입니다. 대신에 그들은 (광분극에서처럼) 그것을 관찰함으로써 상태를 바꿉니다. 아래 그림에서 x와 z는 (불균질한) 자기장의 방향을 지정하며, x-z-평면은 입자 빔과 직교합니다. 아래에 표시된 세 개의 S-G 시스템에서 교차 해치 사각형은 주어진 출력의 차단을 나타냅니다. 즉, 차단기가 있는 각 S-G 시스템은 두 가지 상태 중 하나를 가진 입자만 시퀀스의 다음 S-G 장치에 들어갈 수 있습니다.^[9]

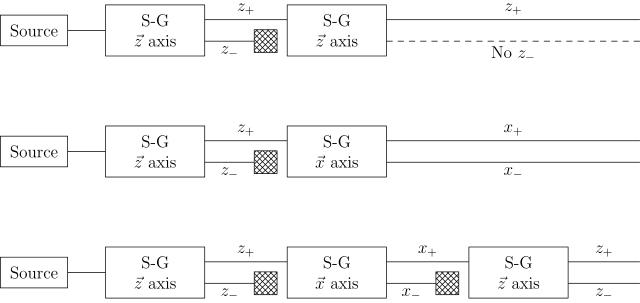
실험1

상단 그림은 동일한 두 번째 S-G 장치를 제 1 장치의 출구에 배치했을 때 두 번째 장치의 출력에 z+만 표시되는 것을 보여줍니다. 이 결과는 첫 번째 장치의 z+ 빔만 두 번째 장치에 들어갔기 때문에 이 지점의 모든 중성자가 z+ 스핀을 가질 것으로 예상되기 때문에 예상됩니다.^[10]

실험2

중간 시스템은 다른 S-G 장치를 z+ 빔의 출구에 배치하여 z 축 대신 x 축에서 빔의 편향을 측정하는 두 번째 장치의 결과로 발생하는 것을 보여줍니다. 두 번째 장치는 x+ 및 x- 출력을 생성합니다. 이제 고전적으로 우리는 x 특성 방향 +와 z 특성 방향 +를 가진 하나의 빔과 x 특성 방향 - 및 z 특성 방향 ^[10]+를 가진 다른 빔을 가질 것으로 예상합니다.

실험3

하위 시스템은 그 기대와 모순됩니다. z 축의 편향을 다시 측정하는 세 번째 장치의 출력은 z- 뿐만 아니라 z+의 출력을 보여줍니다. 두 번째 S-G 장치에 대한 입력이 z+로만 구성된 것을 고려하면, S-G 장치가 이 장치를 통과하는 입자의 상태를 변경하고 있음을 추론할 수 있습니다. 이 실험은 불확정성 원리를 보여주는 것으로 해석할 수 있습니다: 각운동량을 두 개의 수직 방향에서 동시에 측정할 수 없기 때문에 x 방향의 각운동량을 측정하면 z 방향의 각운동량에 대한 이전의 결정이 파기됩니다. 그렇기 때문에 세 번째 장치는 x 측정과 같은 갱신된 z+ 및 z- 빔을 측정하여 z+ 출력을 완전히 슬레이트로 만들었습니다.^[10]

역사

슈테른-게를라흐 실험은 1921년 오토 슈테른에 의해 구상되었고 1922년 프랑크푸르트에서 발터 게를라흐와 함께 공연되었습니다.^[9] 당시 스턴은 프랑크푸르트 대학의 이론물리학 연구소에서 맥스 보른의 조수로 있었고,^[3] 제를라흐는 같은 대학의 실험물리학 연구소에서 조수로 있었습니다.^[3]

실험 당시 원자를 묘사하는 가장 보편적인 모델은 보어-소머펠트 모델로,^[11][12] 전자는 특정한 이산 원자 궤도 또는 에너지 수준에서만 양전하를 띤 핵 주위를 도는 것으로 묘사되었습니다. 전자가 공간의 특정 위치에만 있도록 양자화되었기 때문에 서로 다른 궤도로 분리되는 것을 공간 양자화라고 불렀습니다. 스턴-게를라흐 실험은 은 원자의 각운동량 방향이 양자화된다는 보어-소머펠트 가설을 검증하기 위한 것이었습니다.^[13]

이 실험은 1925년 조지 울렌벡과 새뮤얼 구즈미트가 전자 스핀의 존재에 대한 가설을 공식화하기 몇 년 전에 수행되었음을 주목하십시오.^[14] 슈테른-게를라흐 실험의 결과가 나중에 스핀-1 ⁄2 입자에 대한 양자역학의 예측과 일치하는 것으로 밝혀졌지만, 실험 결과 역시 보어-소머펠트 이론과 일치했습니다.

In 1927, T.E. Phipps and J.B. 테일러는 바닥 상태에서 수소 원자를 사용하여 효과를 재현함으로써 은 원자의 사용으로 인해 발생했을 수 있는 의심을 제거했습니다.^[16] 그러나 1926년 비 상대론적 슈뢰딩거 방정식은 바닥 상태에서 수소의 자기 모멘트를 0으로 잘못 예측했습니다. 이 문제를 해결하기 위해 볼프강 파울리는 "손으로"라는 이름을 가진 파울리 행렬 3개를 소개했지만, 1928년 폴 디랙에 의해 상대론적 방정식에서 본질적인 것으로 나타났습니다.^{[17][self-published source?]}

실험은 먼저 불균일한 자기장을 Null 값에서 점진적으로 켜지도록 하는 전자석으로 수행되었습니다.^[1] 필드가 null일 때 은 원자는 검출 유리 슬라이드에 단일 밴드로 증착되었습니다. 필드를 더 강하게 만들었을 때 밴드의 중간이 넓어지기 시작했고 결국 둘로 갈라져서 유리슬라이드 이미지는 립프린트처럼 보였고 중간에 개구가 있었고 양쪽 끝이 닫혀 있었습니다.^[18] 빔이 두 개로 쪼개질 정도로 자기장이 강한 가운데, 통계적으로 은 원자의 절반이 자기장의 불균일성에 의해 굴절되었습니다.

중요성

슈테른-게를라흐 실험은 이후 현대 물리학의 발전에 큰 영향을 미쳤습니다.

• 그 후 10년 동안 과학자들은 비슷한 기술을 사용하여 일부 원자의 핵도 양자화된 각운동량을 가지고 있다는 것을 보여주었습니다.^{[example needed]} 분광선의 초미세 구조를 담당하는 것은 이 핵 각운동량과 전자의 스핀의 상호작용입니다.^[19]
• 1930년대에, Isidor Rabi와 동료들은 Stern-Gerlach 장치의 확장된 버전을 사용하여 다양한 자기장을 사용함으로써 자기 모멘트를 한 상태에서 다른 상태로 강제로 이동시킬 수 있다는 것을 보여주었습니다.^{[citation needed]} 일련의 실험은 1937년에 시간 가변 필드 또는 RF 필드를 사용하여 상태 전이를 유도할 수 있다는 것을 발견하면서 절정에 이르렀습니다. 이른바 라비 진동은 병원에서 볼 수 있는 자기 공명 영상 장비의 작동 메커니즘입니다.^{[citation needed]}
• 노먼 F. 램지는 후에 라비 장치를 수정하여 현장과의 상호 작용 시간을 늘렸습니다. 방사선의 진동수로 인한 극도의 감도 때문에 정확한 시간을 유지하는 데 매우 유용하며, 오늘날에도 원자시계에서 사용되고 있습니다.^{[citation needed]}
• 60년대 초, 램지와 다니엘 클레프너는 스턴-게를라흐 시스템을 사용하여 여전히 가장 일반적인 주파수 표준 중 하나인 수소 마커의 에너지원으로 편광된 수소 빔을 생성했습니다.
• 스핀을 직접 관찰하는 것은 양자역학에서 양자화의 가장 직접적인 증거입니다.^{[why?][citation needed]}
• Stern-Gerlach 실험은 초기에 알려지지 않은 물리적 특성의 단일 실제 값(eigen value)의 관찰을 보여주는 양자 측정의^[20][21][22] 프로토타입이 되었습니다. 스턴-게를라흐 자석에 들어가면 은 원자의 자기 모멘트의 방향은 부정적이지만 자석의 출구에서 자기장의 방향인 B와 평행하거나 반평행하는 것으로 관찰됩니다. 자기모멘트가 B와 평행한 원자는 자기장 구배에 의해 그 방향으로 가속되었고, 반평행모멘트가 있는 원자는 반대 방향으로 가속되었습니다. 따라서 자석을 통과하는 각 원자는 검출기(그림의 5)를 두 지점 중 한 곳에서만 타격하게 됩니다. 양자 측정 이론에 따르면 원자의 자기 모멘트를 나타내는 파동함수는 자석으로 들어가는 두 방향의 중첩 상태에 있습니다. 운동량 양자가 자기장에서 원자로 전달되어 가속도와 변위를 시작할 때 스핀 방향의 단일 고유값이 기록됩니다.^[23]

참고 항목

• 광자 편광
• 슈테른-게를라흐 훈장
• 독일의 발명가와 발견자들

참고문헌

더보기

• Devereux, M. (2015). "Reduction of the atomic wavefunction in the Stern-Gerlach magnetic field". Canadian Journal of Physics. 93 (11): 1382–1390. Bibcode:2015CaJPh..93.1382D. doi:10.1139/cjp-2015-0031. hdl:1807/69186.
• [1]
• Friedrich, B.; Herschbach, D. (2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today. 56 (12): 53. Bibcode:2003PhT....56l..53F. doi:10.1063/1.1650229. S2CID 17572089.
• Reinisch, G. (1999). "Stern–Gerlach experiment as the pioneer—and probably the simplest—quantum entanglement test?". Physics Letters A. 259 (6): 427–430. Bibcode:1999PhLA..259..427R. doi:10.1016/S0375-9601(99)00472-7.
• Venugopalan, A. (1997). "Decoherence and Schrödinger-cat states in a Stern−Gerlach-type experiment". Physical Review A. 56 (5): 4307–4310. Bibcode:1997PhRvA..56.4307V. doi:10.1103/PhysRevA.56.4307.
• Hsu, B.; Berrondo, M.; Van Huele, J.-F. (2011). "Stern-Gerlach dynamics with quantum propagators". Physical Review A. 83 (1): 012109–1–12. Bibcode:2011PhRvA..83a2109H. doi:10.1103/PhysRevA.83.012109.
• Jeremy Bernstein (2010). "The Stern Gerlach Experiment". arXiv:1007.2435v1 [physics.hist-ph].

외부 링크

• 스턴-게를라흐 실험 - 물리학에 관한 파인만 강의
• 스턴-게를라흐 실험 자바 애플릿 애니메이션
• 스턴-게를라흐 실험 플래시 모델
• 스턴-게를라흐 실험에 대한 상세한 설명
• 올바른 실험, 잘못된 이론: plato.stanford.edu 의 스턴-게를라흐 실험
• 스핀과 연계된 애니메이션, 애플리케이션 및 연구(Université Paris Sud)