양자역학의 역사

History of quantum mechanics
참고 항목:양자역학 연표, 물리학의 역사, 양자장론의 역사
양자역학 역사상 가장 영향력 있는 인물 10인왼쪽에서 오른쪽으로: 막스 플랑크, 알베르트 아인슈타인, 닐스 보어, 루이 드 브로글리, 막스 보른, 폴 디랙, 베르너 하이젠베르크, 볼프강 파울리, 에르빈 슈뢰딩거, 리처드 파인만.

양자역학의 역사는 현대 물리학의 역사의 근본적인 부분입니다.이 역사의 주요 장들은 흑체 복사, 광전 효과, 태양 방출 스펙트럼과 같은 개별적인 현상을 설명하기 위한 양자 아이디어의 출현으로 시작됩니다. 이 시대는 올드 또는 올드 양자 [1]이론이라고 불립니다.슈뢰딩거에 의한 파동 역학의 발명과 다른 많은 사람들에 의해 확장된 것은 1925년경에 시작된 "현대" 시대를 촉발합니다.디랙의 상대론적 양자 이론 연구는 그가 방사선의 양자 이론을 탐구하도록 이끌었고, 최초의 양자장 이론인 양자 전기 역학에서 정점을 찍었습니다.양자역학의 역사는 양자장론의 역사에서 계속됩니다.양자 화학의 역사, 화학 구조, 반응성 및 결합의 이론적 기초는 이 기사에서 논의된 사건과 맞물립니다.

양자역학이라는 용어는 1920년대 초 괴팅겐 대학교에서 막스 보른, 베르너 하이젠베르크, 볼프강 파울리를 포함한 물리학자들에 의해 만들어졌으며, 1924년 보른의 논문 "Zur Quantenmechanik"[2][3]에서 처음 사용되었습니다.

퀀텀이라는 단어는 라틴어로 "얼마나"를 의미합니다.플랑크의 조화 진동자의 에너지로 양자화된 것은 특정 값만 취할 수 있습니다.예를 들어, 대부분의 국가에서 화폐는 효과적으로 계량화되며, 화폐의 양자는 유통되는 가장 낮은 가치의 동전입니다.역학은 물체에 대한 힘의 작용을 다루는 과학의 한 분야입니다.양자역학은 특정한 성질이 양자화된 물체를 다루는 역학의 한 부분입니다.

고전 시대의 끝에 있는 승리와 문제

19세기의 발견, 성공과 실패 모두 양자역학의 출현을 위한 발판을 마련했습니다.

빛의 파동 이론

1670년에 시작하여 30년에 걸쳐 진행된 아이작 뉴턴은 그 당시 어떤 파동 이론도 [1]: 19 직선 이동을 증명하지 못했기 때문에 반사의 완벽한 직선이 빛의 입자 특성을 보여준다고 주장하면서 그의 분자 이론을 개발하고 옹호했습니다.그는 빛의 입자들이 더 밀도가 높은 매질에 들어갈 때 옆으로 가속된다고 가정함으로써 굴절을 설명했습니다.비슷한 시기에, 뉴턴의 동시대의 로버트 훅과 크리스티안 하위헌스, 그리고 후에 아우구스틴-장 프레넬은 빛이 다른 매체에서 다른 속도로 이동한다면 굴절은 빛의 전파의 중간 의존적인 전파로 쉽게 설명될 수 있다는 것을 보여주면서 파동 관점을 수학적으로 개선했습니다.결과적으로 Huygens-Fresnel 원리는 빛의 행동을 재현하는 데 매우 성공적이었고 토머스 영이 1801년 [4]그의 이중 슬릿 실험에 의해 빛의 파동 간섭을 발견한 것과 일치했습니다.파동관은 광선과 입자관을 즉시 대체하지는 않았지만, 19세기 중반에 빛에 대한 과학적 사고를 지배하기 시작했습니다. 왜냐하면 그것은 대안들이 설명할 [5]수 없는 편광 현상을 설명할 수 있었기 때문입니다.

제임스 클러크 맥스웰은 진동하는 전기장과 자기장의 자기 전파 파동을 설명하기 위해 약간의 수정과 함께 이전에 발견된 맥스웰 방정식을 적용할 수 있다는 것을 발견했습니다.가시광선, 자외선, 적외선이 모두 다른 [1]: 272 주파수의 전자파라는 것이 빠르게 밝혀졌습니다.이 이론은 양자역학의 초기에 중요한 요소가 되었습니다.

신흥 원자론

19세기 초, 존 돌턴과 아메데오 아보가드로에 의한 화학 연구는 제임스 클러크 맥스웰, 루트비히 볼츠만과 다른 사람들이 기체의 운동 이론을 확립하기 위해 구축한 아이디어인 물질의 원자 이론에 무게를 실어주었습니다.운동 이론의 성공은 물질이 원자로 구성되어 있다는 생각에 더 신뢰를 주었지만, 그 이론은 또한 양자 [6]역학의 발전에 의해서만 해결될 수 있는 단점들을 가지고 있었습니다.원자의 존재는 물리학자나 화학자들 사이에서 보편적으로 받아들여지지 않았습니다; 예를 들어, Ernst Mach는 확고한 [7]반원자주의자였습니다.

Boltzmann's iodine molecule model
루드비히 볼츠만이 1898년에 제안한 I 분자의2 도표는 원자 "민감한 영역" (α, β)을 겹쳐서 보여줍니다.

루드비히 볼츠만은 1877년에 분자와 같은 물리적 시스템의 에너지 수준이 연속적이기보다는 이산적일 수 있다고 제안했습니다.요오드 가스와 같은 분자에 이산 에너지 수준의 존재에 대한 볼츠만의 이론적 근거는 통계적 열역학과 통계역학 이론에서 비롯되었으며 수학적 주장에 의해 뒷받침되었습니다. 20년 후 맥스 플랑크가 제시한 첫 양자 이론에서도 마찬가지입니다.

전자

1800년대의 마지막 날에, J.J. 톰슨은 전자가 1,000배 이상의 질량을 가지면서 수소 이온과 반대로 같은 크기의 전하를 전달한다는 것을 확립했습니다.많은 그러한 전자들이 모든 [1]: 365 원자와 연관되어 있는 것으로 알려져 있습니다.

복사 이론

Blackbody radiation curve
온도가 낮아짐에 따라 흑체 복사 곡선의 피크는 긴 파장으로 이동하고 강도도 낮아집니다.왼쪽의 흑체 복사 곡선(1862)은 오른쪽에 표시된 레일리 및 청바지(1900)의 초기 고전적 한계 모델과도 비교됩니다.곡선의 단파장 측면은 이미 1896년 빈 분포 법칙에 의해 근사화되었습니다.

1800년대 전반에 걸쳐 많은 연구들이 불꽃, 태양 또는 빨갛게 뜨거운 [1]: 367 물체에 의해 방출되는 빛에 대한 강도 대 주파수 스펙트럼의 세부 사항을 조사했습니다. 리드버그의 공식은 스펙트럼에서 보이는 어두운 선을 효과적으로 요약했지만, 는 그것을 설명할 물리적 모델을 제공하지 않았습니다.붉고 뜨거운 물체에 의해 방출된 스펙트럼은 높은 파장이나 낮은 파장에서 설명될 수 있지만 두 이론은 다릅니다.

고대 양자론

양자 역학은 두 가지 다른 단계로 발전했습니다.오래된 양자 이론으로 알려진 첫 번째 단계는 1900년대에 1800년대의 [1]고전 역학에 의해 이해되지 않는 물리적 현상에 대한 근본적으로 새로운 접근법으로 시작되었습니다.

막스 플랑크는 흑체 복사를 설명하기 위해 양자를 도입했습니다.

주요 기사:자외선 대재앙
플랑크의 젊은 시절 옆모습, 1878년경.
뜨거운 금속 세공.노란색-주황색 빛은 높은 온도로 인해 방출되는 열복사의 가시적인 부분입니다.사진 속의 다른 모든 것들도 열복사로 빛나고 있지만, 인간의 눈이 감지할 수 있는 것보다 덜 밝고 긴 파장에서 빛나고 있습니다.원적외선 카메라는 이 방사선을 관찰할 수 있습니다.

열복사는 물체의 내부 에너지로 인해 물체의 표면에서 방출되는 전자기 복사입니다.만약 물체가 충분히 가열되면, 그것은 붉게 뜨거워지면서 가시광선의 붉은 끝에서 빛을 방출하기 시작합니다.

가열하면 점점 더 짧은 파장(높은 주파수)에서 빛을 방출하기 때문에 색상이 빨간색에서 노란색, 흰색 및 파란색으로 변경됩니다.완벽한 방사체는 완벽한 흡수체이기도 합니다: 그것이 추울 때, 그러한 물체는 완벽하게 검은색으로 보입니다. 왜냐하면 그것은 그것 위에 떨어지는 모든 빛을 흡수하고 방출하지 않기 때문입니다.결과적으로, 이상적인 열 방출체는 흑체라고 알려져 있고, 그것이 방출하는 방사선은 흑체 복사라고 불립니다.

물체가 방출하는 다양한 주파수의 열복사량에 대한 예측.플랑크의 법칙에 의해 예측된 정확한 값(녹색)은 레일리-진스 법칙(빨간색) 및 빈 근사(파란색)의 고전적인 값과 대조됩니다.

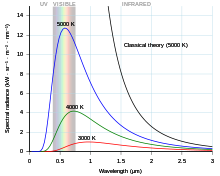
19세기 후반까지, 열복사는 실험적으로 꽤 잘 특성화되었습니다.복사가 온도에 따라 가장 강하게 변하는 파장이 빈의 변위 법칙에 의해 어떻게 주어지는지, 단위 면적당 방출되는 전체 전력은 스테판-볼츠만 법칙에 의해 주어지는지, 열복사의 실험 측정 중 일부를 설명할 수 있는 몇 가지 공식이 만들어졌습니다.실험 결과에 대한 가장 좋은 이론적 설명은 큰 파장(또는 동등하게 낮은 주파수)에서는 실험 결과와 잘 일치하지만 짧은 파장(또는 높은 주파수)에서는 강하게 동의하지 않는 레일리-진스 법칙이었습니다.사실, 짧은 파장에서, 고전 물리학은 에너지가 뜨거운 물체에 의해 무한한 속도로 방출될 것이라고 예측했습니다.분명히 잘못된 이 결과는 자외선 재앙으로 알려져 있습니다.그러나 고전 물리학은 그림과 같이 낮은 주파수에서는 실험 결과와 잘 일치하지만 높은 주파수에서는 강하게 동의하지 않는 레일리-진스 법칙으로 이어졌습니다.물리학자들은 모든 실험 결과를 설명하는 단일 이론을 찾았습니다.

흑체 복사 강도 대 색과 온도.무지개 막대는 가시광선을 나타냅니다. 5000K 개체는 가시광선의 다른 색상을 혼합하여 "흰색 핫" 상태입니다.오른쪽은 보이지 않는 적외선입니다.고전 이론(5000K에 대한 검정 곡선)은 실패합니다. 다른 곡선은 플랑크의 법칙에 의해 정확하게 예측됩니다.

열복사의 전체 스펙트럼을 설명할 수 있었던 첫 번째 모델은 [8]1900년에 막스 플랑크에 의해 제시되었습니다.그는 열복사가 조화 진동자 세트와 평형을 이루는 수학적 모델을 제안했습니다.실험 결과를 재현하기 위해, 그는 임의의 양의 에너지를 방출할 수 있는 대신 각 발진기가 단일 특성 주파수에서 정수 단위의 에너지를 방출한다고 가정해야 했습니다.즉, 발진기에서 방출되는 에너지는 양자화되었습니다.플랑크에 따르면, 각 발진기의 에너지 양자는 발진기의 주파수에 비례했습니다; 비례 상수는 현재 플랑크 상수로 알려져 있습니다.

플랑크의 법칙은 물리학에서 최초의 양자론이었고, 플랑크는 1918년에 "에너지 [9]양자의 발견으로 물리학의 발전에 기여한 공로를 인정받아" 노벨상을 수상했습니다.그러나, 그 당시 플랑크의 견해는 양자화가 (지금은 믿어지고 있는) [10]세계에 대한 우리의 이해의 근본적인 변화라기보다는 순전히 발견적인 수학적 구성이라는 것이었습니다.

알버트 아인슈타인은 광전 효과를 설명하기 위해 양자를 적용합니다.

주요 기사:광전 효과
빛은 왼쪽에서 표면에 비칩니다.광 주파수가 충분히 높으면, 즉 충분한 에너지를 전달하면 음전하를 띤 전자가 금속에서 방출됩니다.

1887년 하인리히 헤르츠는 충분한 주파수를 가진 빛이 금속 표면에 닿으면 표면이 음극선을 [1]: I:362 방출한다는 것을 관찰했습니다.10년 후, J.J. 톰슨은 음극선의 많은 보고들이 실제로는 "군체"였고 그것들은 빠르게 전자라고 불리게 되었다는 것을 보여주었습니다.1902년에, Philipp Lenard는 방출된 전자의 최대 가능한 에너지가 [11]그 강도와 관련이 없다는 것을 발견했습니다.이 관측은 전자의 에너지가 입사 [12]: 24 방사선의 강도에 비례해야 한다고 예측하는 고전적인 전자기학과 상충됩니다.

알베르트 아인슈타인 1905

1905년에, 알버트 아인슈타인은 빛의 연속적인 모델이 시간 평균 광학 현상에 매우 잘 작용했음에도 불구하고, 순간적인 전환의 경우 빛 속의 에너지는 유한한 수의 에너지 [13]양자를 발생시킬 수 있다고 제안했습니다.아인슈타인은 1905년 3월 양자 논문 "빛의 방출과 변환에 관한 발견적 관점"의 도입부에서 다음과 같이 말합니다.

여기서 고려해야 할 가정에 따르면, 어떤 점에서 광선이 퍼질 때, 그 에너지는 끊임없이 증가하는 공간에 지속적으로 분포되지 않고, 공간의 점에 국한되어 분할하지 않고 이동하며, 전체적으로만 흡수되거나 생성될 수 있는 유한한 수의 "에너지 양자"로 구성됩니다.

이 진술은 [14]20세기의 물리학자에 의해 쓰여진 가장 혁명적인 문장이라고 불립니다. f fdisplaystyle f\ f\ hdisplaystyle h\displaystyle h\displaystyle h\displaystyle h\displaystyle h}(극히 작은 양수)를 곱한 주파수로

아인슈타인은 가벼운 양자가 그것의 모든 에너지를 하나의 전자로 전달하여 전자에 최대로 에너지 hf를 부여한다고 가정했습니다.따라서 광 주파수만이 전자에 전달될 수 있는 최대 에너지를 결정합니다. 광 방출의 강도는 광빔 [13]강도에 비례합니다.

아인슈타인은 [15]금속에서 전자를 제거하기 위해서는 작업 함수라고 불리며 π로 표시되는 일정한 양의 에너지가 필요하다고 주장했습니다.이 에너지의 양은 금속마다 다릅니다.광 양자의 에너지가 작업 함수보다 작으면 금속에서 전자를 제거할 만큼 충분한 에너지를 전달하지 못합니다.임계값 주파수 f는0 에너지가 작업 함수와 동일한 광 양자의 주파수입니다.

f가 f보다 크면 에너지0 hf는 전자를 제거하기에 충분합니다.방출된 전자는 운동 에너지 E를K 가지며, 이는 기껏해야 빛 에너지에서 금속에서 전자를 제거하는 데 필요한 에너지를 뺀 값과 같습니다.

빛이 에너지 양자로 구성되어 있다는 아인슈타인의 설명은 플랑크의 양자화된 에너지 개념을 확장시켰는데, 이는 주어진 주파수의 단일 양자 f가 불변의 양의 에너지 hf를 전달한다는 것입니다.본질적으로 단일 양자는 거의 발견되지 않습니다.19세기에 이용 가능한 태양과 방출원은 매 초마다 엄청난 양의 에너지를 방출합니다.플랑크 상수 h는 너무 작아서 각 양자 hf의 에너지 양이 매우 작습니다.우리가 보는 빛은 수조 개의 그러한 양자를 포함합니다.

물질의 양자화: 원자의 보어 모델

주요 기사:보어 모형

20세기 초까지, 증거는 작고 밀도가 높고 양전하를 띤 핵을 둘러싸고 음전하를 띤 전자 구름이 있는 원자의 모델을 요구했습니다.이러한 특성은 전자가 별 주위를 도는 행성처럼 핵 주위를 도는 모델을 제안했습니다.원자의 고전적인 모델은 1911년에 원자핵의 존재를 처음으로 증명한 가이거-마르스덴 금박 실험에 기초하여 제안한 어니스트 러더퍼드의 이름을 따서 행성 모델 또는 때때로 러더퍼드 모델이라고 불립니다.그러나, 이 모델의 원자는 또한 불안정할 것이라고 알려져 있었습니다: 고전 이론에 따르면 궤도를 도는 전자는 구심 가속도를 받고 있기 때문에 전자기 복사를 방출해야 합니다. 에너지 손실은 또한 핵을 향해 나선형으로 회전하여 1초의 몇 분의 1초 안에 충돌하게 만듭니다.

두 번째 관련 퍼즐은 원자의 방출 스펙트럼이었습니다.가스가 가열될 때, 그것은 오직 별개의 주파수에서만 빛을 발산합니다.예를 들어, 수소에 의해 방출되는 가시광선은 아래 그림과 같이 네 가지 다른 색으로 구성되어 있습니다.다른 주파수에서의 빛의 세기 또한 다릅니다.대조적으로, 백색광은 가시적인 주파수의 전체 범위에 걸쳐 연속적인 방출로 구성됩니다.19세기 말까지, 발머 공식으로 알려진 간단한 규칙은 서로 다른 선의 주파수가 서로 어떻게 관련되어 있는지를 보여주었지만, 왜 그런지 설명하거나 강도에 대한 예측은 하지 않았습니다.이 공식은 또한 당시에 관측되지 않았던 자외선과 적외선의 추가 스펙트럼 라인을 예측했습니다.이 선들은 나중에 실험적으로 관찰되어 공식의 값에 대한 신뢰도를 높였습니다.

수소의 방출 스펙트럼.수소 가스는 들뜨면 가시 스펙트럼에서 네 가지 다른 색(분광선)과 적외선 및 자외선에서 여러 선으로 빛을 발산합니다.
수소의 방출 스펙트럼을 설명하는 수학적 공식

1885년에 스위스 수학자 요한 발머는 수소의 가시적 스펙트럼에서 각각의 파장 γ (lambda)가 어떤 정수 n과 관련이 있다는 것을 발견했습니다.

여기서 B는 364.56 nm와 동일하다고 결정된 상수 발머입니다.

1888년에 요하네스 리드버그는 발머 공식의 설명적 유용성을 일반화하고 크게 증가시켰습니다.그는 오늘날 뤼드베르크 [16]공식으로 알려진 것에 따라 λ가 두 정수 n과 m과 관련이 있다고 예측했습니다.

여기서 R은 Rydberg 상수이며, 0.0110−1 nm와 같고, n은 m보다 커야 합니다.

리드버그의 공식은 m = 2와 n = 3, 4, 5, 6을 설정함으로써 네 개의 가시적인 수소 파장을 설명합니다.또한 방출 스펙트럼의 추가 파장을 예측합니다. 형태 = 1 및 n > 1의 경우 방출 스펙트럼은 특정 자외선 파장을 포함해야 하며 형태 = 3 및 n > 3의 경우 특정 적외선 파장도 포함해야 합니다.이 파장들에 대한 실험적인 관찰은 20년 후에 이루어졌습니다: 1908년에 루이스 파셴은 예측된 적외선 파장의 일부를 발견했고 1914년에 테오도어 라이먼은 예측된 자외선 [16]파장의 일부를 발견했습니다.

발머와 리드버그의 공식은 모두 정수를 포함합니다: 현대 용어로, 그들은 원자의 일부 특성이 양자화됨을 암시합니다.이 특성이 무엇인지, 그리고 왜 양자화되었는지 정확히 이해하는 것은 이 기사의 나머지 부분에서 보여지듯이 양자역학의 발전에 중요한 부분이었습니다.

1905년, 알버트 아인슈타인은 브라운 운동을 설명하기 위해 운동 이론을 사용했습니다.프랑스 물리학자 장 바프티스테 페랭은 아인슈타인의 논문에 있는 모델을 사용하여 원자의 질량과 크기를 실험적으로 결정하여 원자 [citation needed]이론에 대한 직접적인 경험적 검증을 제공했습니다.

Bohr model of hydrogen atom
닐스 보어의 1913년 수소 원자 양자 모델.

1913년에 닐스 보어는 양자화된 전자 궤도를 포함하는 원자의 새로운 모델을 제안했습니다: 행성들이 태양 주위를 도는 것처럼 전자는 여전히 핵 주위를 돌고 있지만, 그들은 임의의 [17]거리에서 궤도를 도는 것이 아니라 특정한 궤도에만 거주하는 것이 허용됩니다.원자가 에너지를 방출(또는 흡수)했을 때, 전자는 고전적으로 예상되는 것처럼 핵 주위의 한 궤도에서 다른 궤도로 연속적으로 이동하지 않았습니다.대신,[18] 전자는 광자의 형태로 방출된 빛을 발산하면서 한 궤도에서 다른 궤도로 순간적으로 뛰어오를 것입니다.각 원소에 의해 방출되는 광자의 가능한 에너지는 궤도 사이의 에너지 차이에 의해 결정되었고, 따라서 각 원소에 대한 방출 스펙트럼은 많은 [19]선을 포함할 것입니다.

Head and shoulders of a young man in a suit and tie
젊은 시절의 닐스 보어

궤도가 따라야 하는 규칙에 대한 단 하나의 간단한 가정에서 시작하여, 보어 모델은 수소의 방출 스펙트럼에서 관찰된 스펙트럼 라인을 이전에 알려진 상수와 연관시킬 수 있었습니다.보어의 모델에서, 전자는 지속적으로 에너지를 방출하고 핵에 충돌하는 것이 허용되지 않았습니다: 일단 그것이 가장 가까운 허용 궤도에 있게 되면, 그것은 영원히 안정적이었습니다.보어의 모델은 궤도가 왜 그런 식으로 양자화되어야 하는지 설명하지 못했고, 두 개 이상의 전자를 가진 원자에 대한 정확한 예측을 할 수도 없었고, 일부 스펙트럼 라인이 다른 것보다 더 밝은 이유를 설명할 수도 없었습니다.

보어 모델의 일부 기본적인 가정은 곧 틀렸다는 것이 증명되었지만 방출 스펙트럼의 이산 선이 양자화되는 원자에 있는 전자의 일부 특성 때문이라는 핵심 결과는 정확합니다.전자가 실제로 행동하는 방식은 보어의 원자와 놀랍도록 다르고, 우리가 일상적인 경험의 세계에서 보는 것과 다릅니다. 이 원자의 현대 양자 역학 모델은 아래에서 논의됩니다.

Bohr 모델에 대한 더 자세한 설명

보어는 전자의 각운동량 L이 양자화된다는 이론을 세웠습니다.

여기서 n은 정수이고 h는 플랑크 상수와 플랑크 감소 상수입니다.이 가정을 시작으로, 쿨롱의 법칙과 원운동 방정식은 n 단위의 각운동량을 가진 전자가 다음과 같은 거리 r에서 양성자를 공전한다는 것을 보여줍니다.

2 2 {{ r = ^{

여기서e k는 쿨롱 상수, m은 전자의 질량, e는 전자에 대한 전하입니다.단순화를 위해 다음과 같이 기록됩니다.

여기서0 보어 반지름이라고 하는 a는 0.0529 nm와 같습니다.보어 반지름은 허용되는 가장 작은 궤도의 반지름입니다.

전자의 에너지는 운동 에너지와 퍼텐셜 에너지의 합입니다.전자는 핵 주위의 실제 운동으로 인한 운동 에너지와 핵과의 전자기적 상호작용으로 인한 전위 에너지를 가집니다.보어 모델에서 이 에너지는 다음과 같이 계산될 수 있습니다.

- 1 {{ E=-{\ e

따라서 각운동량이 양자화된다는 보어의 가정은 전자가 핵 주위의 특정 궤도에만 거주할 수 있고 특정 에너지만 가질 수 있다는 것을 의미합니다.이러한 제약의 결과는 전자가 핵에 충돌하지 않는다는 것입니다: 전자는 지속적으로 에너지를 방출할 수 없고, a(보어 반지름)보다0 핵에 더 가까이 다가갈 수 없습니다.

전자는 그것의 원래 궤도에서 낮은 궤도로 순간적으로 점프함으로써 에너지를 잃습니다; 여분의 에너지는 광자의 형태로 방출됩니다.반대로, 광자를 흡수하는 전자는 에너지를 얻고, 그래서 그것은 핵으로부터 더 먼 궤도로 뛰어오릅니다.

빛나는 원자 수소에서 나오는 각 광자는 반지름 r이n 있는 더 높은 궤도에서 더 낮은 궤도m r로 이동하는 전자 때문입니다.이 광자의 에너지γ E는 전자의 에너지n E와m E의 차이입니다.

플랑크 방정식은 광자의 에너지가 E = hc/π에 의해γ 파장과 관련이 있다는 것을 보여주기 때문에, 방출될 수 있는 빛의 파장은 다음과 같습니다.

이 방정식은 Rydberg 공식과 동일한 형태를 가지며, 상수 R은 다음과 같이 주어져야 한다고 예측합니다.

따라서 원자의 보어 모델은 기본 상수의 관점에서 수소의 방출 스펙트럼을 예측할 수 있습니다.이 모델은 핵과 단일 전자(즉, 하나의 전자만 포함하는 He 또는7+ O와 같은+ 이온)로 구성된 시스템의 방출 스펙트럼을 설명하기 위해 쉽게 수정될 수 있지만 중성 헬륨과 같은 두 개의 전자를 가진 원자로 확장될 수 없습니다.하지만, 그것은 다중 전자 원자에 대한 정확한 예측을 하거나, 왜 일부 스펙트럼 라인이 다른 것보다 더 밝은지 설명할 수 없었습니다.


1911년의 첫 솔베이 회의에서 양자 이론의 진화에서 중요한 단계가 취해졌습니다.그곳에서 과학계의 최고 물리학자들이 "방사능과 퀀타"의 문제를 논의하기 위해 모였습니다.이 때까지 원자의 어니스트 러더퍼드 모델이 [20][21]출판되었지만, 원자 구조와 관련된 많은 논의는 1910년 아서 하스의 양자 모델을 중심으로 진행되었습니다.또한 1911년 솔베이 회의에서 헨드릭 로런츠는 아인슈타인의 양자 구조에 대한 강연 후 회전자의 에너지를 [22][23]: 244 nhv와 동일하게 설정할 것을 제안했습니다.이것은 핵과 이산화된 각운동량이었던 1912년의 [24][25][26]존 윌리엄 니콜슨 모델과 같은 다른 양자 모델이 뒤따랐습니다.니콜슨은 궤도면에 수직인 핵 원자에서 전자의 진동을 사용하여 안정성을 유지함으로써 스펙트럼을 그의 원자 모델에 도입했습니다.니콜슨의 원자 스펙트럼은 태양 스펙트럼과 성운 [24][27][28][23]: 278 스펙트럼에서 많은 분포하지 않은 선을 확인했습니다.

1913년에 보어는 다시 양자화를 사용하여 1913년 7월 원자와 분자의 구성에 관한 논문에서 니콜슨 [29][30][26]모델을 논의하고 인용하면서 수소 원자의 스펙트럼 라인을 설명했습니다.보어 모델에서 수소 원자는 가볍고 음으로 대전된 전자에 의해 궤도를 도는 무겁고 양으로 대전된 핵으로 그려집니다.전자는 감소된 플랑크 상수의 정수 배수로 제한된 각운동량으로 레이블이 지정된 특정하고 이산적으로 분리된 궤도에서만 존재할 수 있습니다.이 모델의 주요 성공은 [23]: 276 궤도 사이의 전자 전환을 사용하여 원자 수소의 스펙트럼 방출선에 대한 뤼드베르크 공식을 설명하는 데 있었습니다.뤼드베르크 공식은 실험적으로 알려져 있었지만, 보어 모델이 도입되기 전까지는 이론적 뒷받침을 얻지 못했습니다.보어 모델은 리드버그 공식의 구조에 대한 이유를 설명했을 뿐만 아니라 공식의 경험적 결과를 구성하는 기본적인 물리 상수에 대한 정당성을 제공했습니다.

게다가 플랑크의 양자 이론을 전자에 적용함으로써 1911-1913년에 테판 프로코피우, 그리고 1913년에 닐스 보어가 나중에 "자석"이라고 불리는 전자의 자기 모멘트를 계산할 수 있게 되었습니다. 유사한 양자 계산이지만, 수치적으로 상당히 다른 값을 가지고,그 후 양성자의 자기 모멘트와 중성자의 자기 모멘트 모두 전자의 자기 모멘트보다 3배 작은 것이 가능해졌습니다.

이 이론들은, 비록 성공적이었지만, 엄격하게 현상학적이었습니다: 이 시기 동안, 아마도 앙리 푸앵카레의 1912년 논문 술라테오리 데 [31][32]퀀타에서 플랑크 이론에 대한 논의를 제외하고는, 양자화에 대한 엄격한 정당성이 없었습니다.그들은 총칭하여 오래된 양자 이론으로 알려져 있습니다.

스핀 양자화

주요 기사: 스핀 (물리학)
참고 항목:스턴-게를라크 실험
스턴-게를라크 실험에서 양자 스핀 대 고전적 자석

전자의 자기 모멘트와 결합된 전자의 궤도 각운동량의 양자화는 자기 모멘트를 가진 원자가 자기장에서 양자화된 행동을 보여야 한다는 것을 제안했습니다.1922년, 오토 스턴과 발터 게라흐는 이 이론을 시험하기 위해 출발했습니다.그들은 일련의 좁고 정렬된 슬릿이 장착된 진공관에서 은을 가열하여 은 원자의 분자 빔을 만들었습니다.그들은 이 빔을 불균일한 자기장을 뚫고 쏘았습니다.그들은 은 원자의 연속적인 패턴이 아닌 두 [33]다발을 발견했습니다.

북극에 비해 위, 아래 또는 그 사이의 어딘가를 가리키며, 고전 역학에서 자기장을 통해 던져진 자석은 위 또는 아래로 작고 큰 거리를 비껴갈 수 있습니다.스턴과 게라흐가 자기장을 통해 쏜 원자도 비슷하게 작용했습니다.하지만, 자석이 다양한 거리를 비껴갈 수 있는 반면, 원자는 항상 일정한 거리를 비껴갈 수 있습니다.이것은 자석의 방향에 해당하는 원자의 특성이 임의의 각도에서 자유롭게 선택되는 것과 반대로 두 가지 값(위 또는 아래) 중 하나를 취하여 양자화되어야 한다는 것을 의미합니다.

스턴-게라흐 실험에 사용된 자기장 방향의 선택은 임의적입니다.여기에 표시된 애니메이션에서는 필드가 수직이기 때문에 원자가 위나 아래로 편향됩니다.자석이 4분의 1 회전하면 원자가 왼쪽 또는 오른쪽으로 꺾입니다.수직 필드를 사용하면 수직 축을 따라 스핀이 양자화됨을 나타내고, 수평 필드를 사용하면 수평 축을 따라 스핀이 양자화됨을 나타냅니다.

스턴-겔라흐 실험의 결과는 센세이션을 일으켰는데, 특히 아인슈타인과 폴 에렌페스트를 포함한 선도적인 과학자들이 은 원자가 실험 조건에서 무작위 방향을 가져야 한다고 주장했기 때문입니다: 양자화는 [33]관찰되어서는 안 됩니다.이 수수께끼가 해결되기까지는 적어도 5년이 걸릴 것입니다. 양자화가 관찰되었지만 궤도 각운동량 때문은 아니었습니다.

1925년에 랄프 크로니그는 전자가 [34]: 56 축을 중심으로 자전하는 것처럼 행동한다고 제안했습니다.스핀은 기존 측정값과 일치하여 스펙트럼 라인을 담당하는 에너지 수준을 분할하는 작은 자기 모멘트를 생성합니다.동일한 궤도에 있는 두 개의 전자가 반대 방향으로 "회전"하면 별개의 양자 상태를 차지하여 배제 원칙을 충족합니다.불행하게도 그 이론은 두 가지 중요한 결함을 가지고 있었습니다: 크로니그에 의해 계산된 두 개의 값이 두 배 차이가 났습니다.크로니그의 선임 동료들은 그의 작품을 낙담시켰고 그것은 출판되지 않았습니다.

10개월 후, 레이던 대학의 네덜란드 물리학자 조지 울렌벡과 새뮤얼 구스미트는 전자 자기 [35]회전 이론을 발표했습니다.크로니그와 같은 모델은 본질적으로 고전적이었지만 양자 예측을 낳았습니다.

드 브로이의 물질 파동 가설

1929년 루이 드 브로이.드 브로이는 1924년 박사 논문에서 물질이 파동으로 작용한다는 예측으로 노벨 물리학상을 수상했습니다.

1924년에 루이 드 브로이는 물질은 파동의 특성을 가지고 있다는 획기적인 가설을 발표했습니다.양자화된 에너지 전달을 사용하여 광전 효과를 설명할 수 있다는 아인슈타인의 제안과 특수 상대성 이론에서 정지 의 질량이 E 에너지와 동등하다는 아인슈타인의 제안을 기반으로 합니다드 브로이는 운동 [36][37]중인 물질이 파장 h / \ \ 와 관련된 파동을 갖는 것으로 제안했습니다.원자를 둘러싸는 데 그의 파장을 요구하면서, 그는 보어의 [1]: 217 궤도의 양자화를 설명했습니다.동시에 이것은 빛의 파동 거동이 본질적으로 양자 [1]: 216 효과라는 것을 보여주었습니다.

De Broglie는 핵 주위의 궤도에 있는 전자가 파동과 같은 특성을 가지고 있다고 생각될 수 있다는 것을 보여줌으로써 원자의 보어 모델을 확장했습니다.특히, 전자는 핵 주위에 정재파를 허용하는 상황에서만 관찰됩니다.정재파의 예로는 바이올린 줄이 있는데, 바이올린 줄은 양쪽 끝에 고정되어 있고 진동하도록 만들 수 있습니다.현악기에 의해 생성된 파동은 제자리에서 진동하는 것처럼 보이며 위아래로 움직입니다.정재파의 파장은 진동하는 물체의 길이와 경계 조건과 관련이 있습니다.예를 들어, 바이올린 줄은 양쪽 끝에 고정되어 있기 때문에 를 전달할 수 있습니다 여기서 l은 길이이고 n은 양의 정수입니다De Broglie는 허용된 전자 궤도는 궤도의 둘레가 파장의 정수 수가 될 것이라고 제안했습니다.따라서 전자의 파장은 핵으로부터 특정 거리의 보어 궤도만이 가능하다는 것을 결정합니다.결과적으로, 특정 값보다 작은 핵으로부터의 거리에서는 궤도를 설정하는 것이 불가능할 것입니다.핵으로부터 가능한 최소 거리를 보어 [38]반경이라고 합니다.드 브로글리의 보어 원자 처리는 궁극적으로 실패했지만, 그의 가설은 슈뢰딩거 파동 방정식의 출발점이 되었습니다.

파동으로 작용하는 물질은 전자에 대해 실험적으로 처음 입증되었습니다: 전자의 빔은 빛이나 물의 빔처럼 회절을 나타낼 수 있습니다.드 브로이가 그의 가설을 발표한 지 3년 후에 두 개의 다른 그룹이 전자 회절을 증명했습니다.애버딘 대학에서 조지 패짓 톰슨과 알렉산더 리드는 전자 빔을 얇은 셀룰로이드 필름을 통과시킨 다음 나중에 금속 필름을 통과시키고 예측된 간섭 패턴을 관찰했습니다. (톰슨의 대학원생이었던 알렉산더 리드,첫 번째 실험을 수행했지만 오토바이 사고로[39] 곧 사망했으며 거의 언급되지 않습니다.)벨 연구소에서 클린턴 조셉 데이비스슨과 레스터 할버트 저머는 [1]: II:218 결정에서 돌아오는 파동 모델에 의해 예측된 잘 정의된 빔을 관찰하면서 니켈 샘플의 전자 빔을 실험에 반영했습니다.드 브로이는 그의 가설로 1929년 노벨 물리학상을 수상했습니다.톰슨과 데이비슨은 그들의 실험적인 연구로 1937년 노벨 물리학상을 공동 수상했습니다.

드 브로이의 접근법을 바탕으로, 현대 양자역학은 1925년 독일 물리학자 베르너 하이젠베르크, 막스 보른,파스쿠알[40][41] 조던은 행렬역학을 발전시켰고, 오스트리아의 물리학자 에르빈 슈뢰딩거는 드 브로이 [42]이론의 일반화된 경우의 근사치로서 파동역학과 비상대론적 슈뢰딩거 방정식을 발명했습니다.슈뢰딩거는 이후 두 접근법이 동등하다는 것을 보여주었습니다.양자역학을 물리적 시스템에 처음 적용한 것은 볼프강[43] 파울리에 의한 수소 스펙트럼의 대수적 결정과 루시 멘싱에 [44]의한 이원자 분자의 처리였습니다.

현대 양자역학의 발전

양자 역학의 첫 번째 시대의 종말은 드 브로글리의 물질 [1]: 268 파동 가설의 출판에 의해 촉발되었고, 슈뢰딩거의 물질에 대한 파동 역학의 발견으로 이어졌습니다.수소의 흡수 스펙트럼에 대한 정확한 예측은 새로운 양자 [1]: 275 이론의 광범위한 수용을 보장했습니다.

행렬역학

주요 기사: 행렬 역학
참고 항목:하이젠베르크의 행렬역학 입문서

1925년, 베르너 하이젠베르크는 수소 방출 스펙트럼에서 서로 다른 선의 강도를 설명하면서 보어 모델이 답하지 않은 문제 중 하나를 해결하려고 시도했습니다.일련의 수학적 유추를 통해,[45] 그는 강도의 고전적인 계산을 위한 양자-기계적 아날로그를 썼습니다.얼마 후, 하이젠베르크의 동료 맥스 보른은 다른 에너지 수준 사이의 전이 확률을 계산하는 하이젠베르크의 방법이 행렬의 수학적 개념을 사용함으로써 가장 잘 표현될 수 있다는 것을 깨달았습니다.

하이젠베르크는 전자의 위치와 운동량을 동시에 측정하려는 사고 실험을 분석하면서 1927년에 불확실성 원리의 초기 버전을 공식화했습니다.그러나, 하이젠베르크는 이러한 측정에서 "불확실성"이 무엇을 의미하는지에 대한 정확한 수학적 정의를 제공하지 않았고, 이는 얼 헤세 케나드, 볼프강 파울리, 헤르만 [46][47]바일에 의해 곧 취해질 단계입니다.

파동역학

1926년 전반기, 에르빈 슈뢰딩거는 드 브로글리의 가설을 바탕으로 양자 역학 [48]파동의 거동을 설명하는 방정식을 개발했습니다.슈뢰딩거 방정식의 창시자의 이름을 따서 슈뢰딩거 방정식이라고 불리는 수학적 모델은 양자 역학의 중심이며, 양자 시스템의 허용된 정지 상태를 정의하고 물리적 시스템의 양자 상태가 [49]시간에 따라 어떻게 변화하는지 설명합니다.파동 자체는 "파동 함수"로 알려진 수학적 함수에 의해 설명됩니다.슈뢰딩거는 파동 함수가 "측정 [50]결과의 확률을 예측하는 수단"을 제공한다고 말했습니다.

슈뢰딩거는 수소 원자의 전자를 고전적인 파동으로 취급하여 수소의 에너지 수준을 계산할 수 있었고, 양성자에 의해 생성된 전위의 우물 안에서 이동했습니다.이 계산은 Bohr 모델의 에너지 수준을 정확하게 재현했습니다.

1926년 5월, 슈뢰딩거는 하이젠베르크의 행렬 역학과 파동 역학이 전자의 특성과 행동에 대해 동일한 예측을 했다는 것을 증명했습니다; 수학적으로, 두 이론은 기본적으로 공통된 형태를 가지고 있었습니다.그러나 두 사람은 그들의 상호 이론의 해석에 대해 의견이 일치하지 않았습니다.예를 들어,[51] 하이젠베르크는 원자의 궤도 사이에서 전자의 점프에 대한 이론적 예측을 받아들였지만, 슈뢰딩거는 연속적인 파동과 같은 특성에 기초한 이론이 그가 "양자 [52]점프에 대한 이러한 넌센스"라고 부르는 것을 피할 수 있기를 희망했습니다.결국 하이젠베르크의 접근법이 승리했고, 양자 점프가 [53]확정됐습니다.

슈뢰딩거와 닐스 보어 연구소의 파동역학

주요 기사:코펜하겐 해석
A block-shaped beige building with a sloped, red-tiled roof
1920년대와 1930년대 양자역학 및 관련 주제 연구자들의 중심지였던 코펜하겐의 닐스 보어 연구소.세계에서 가장 잘 알려진 이론 물리학자들 대부분이 그곳에서 시간을 보냈습니다.

보어, 하이젠베르크, 그리고 다른 사람들은 이 실험 결과와 수학적 모델이 정말로 무엇을 의미하는지 설명하려고 노력했습니다.코펜하겐 해석이라는 용어는 [54][55][56][57][58][59]그들 사이의 차이점을 얼버무리며 그들의 관점을 되돌아보는 데 적용되었습니다."코펜하겐 해석"에 대한 명확한 진술은 없지만, 다음과 같은 생각들이 그것의 특징으로 널리 보입니다.

  1. 시스템은 양자 상태에 의해 완전히 설명됩니다(하이젠베르크).
  2. 시간이 지남에 따라 양자 상태가 어떻게 변화하는지는 빛과 물질에 파동 특성을 부여하는 슈뢰딩거 방정식에 의해 제공됩니다.
  3. 원자 상호작용은 불연속적입니다. (플랑크의 작용 양자)
  4. 자연에 대한 설명은 본질적으로 확률론적입니다.예를 들어, 이중 슬릿 실험에서 입자가 화면에 나타나는 사건의 확률은 파동 함수의 진폭의 절대값의 제곱과 관련이 있습니다. (본 규칙은 코펜하겐 해석에서 파동 함수에 물리적 의미를 부여하는 Max Born으로 인해 발생합니다: 확률 진폭)
  5. 시스템의 호환되지 않는 속성 쌍의 값을 동시에 알 수 없습니다.(하이젠베르크의 불확정성 원리)
  6. 물질은 빛과 마찬가지로 파동-입자 이중성을 나타냅니다.실험은 물질의 입자와 같은 특성 또는 파동과 같은 특성을 보여줄 수 있지만 동시에 둘 다는 아닙니다.(Bohr로[60] 인한 보완성 원칙)
  7. 측정 장치는 본질적으로 고전적인 장치이며 위치 및 운동량과 같은 고전적인 특성을 측정합니다.
  8. 큰 시스템의 양자역학적 설명은 고전적 설명과 밀접하게 유사해야 합니다. (보어와 하이젠베르크의 대응 원리)

수소 원자에 적용

주요 기사:원자 궤도 모형

보어의 원자 모형은 본질적으로 원자핵 "태양" 주위를 도는 전자를 가진 행성 모형이었습니다.하지만, 불확정성 원리는 전자가 행성이 하는 것처럼 정확한 위치와 속도를 동시에 가질 수 없다고 말합니다.고전적인 궤도 대신에, 전자는 원자 궤도에 거주한다고 합니다.궤도는 전자가 발견될 수 있는 가능한 위치의 "구름"으로, 정확한 [61]위치보다는 확률의 분포입니다.각 궤도는 2차원 궤도가 아닌 3차원이며,[62] 종종 전자를 찾을 확률이 95%인 3차원 영역으로 묘사됩니다.

슈뢰딩거는 양성자에 의해 생성된 전위 우물 V에서 수소 원자의 전자를 "파 함수" Δ로 표시되는 파동으로 처리함으로써 수소의 에너지 수준을 계산할 수 있었습니다.슈뢰딩거 방정식의[clarification needed] 해는 전자 위치와 위치에 대한 확률 분포입니다.궤도는 3차원에서 다양한 모양의 범위를 가지고 있습니다.다양한 궤도의 에너지를 계산할 수 있으며 보어 모델의 에너지 수준과 정확하게 일치합니다.

슈뢰딩거의 그림에서 각 전자는 다음과 같은 네 가지 특성을 가집니다.

  1. 입자파가 적은 에너지로 핵에 더 가까운 것인지, 더 많은 에너지로 핵에서 더 먼 것인지를 나타내는 "궤도" 명칭.
  2. 구면 또는 그 밖의 궤도의 "모양"
  3. z축 주위 궤도의 자기 모멘트를 결정하는 궤도의 "경사각"입니다.
  4. 전자의 "스핀".

이러한 성질의 총칭은 전자의 양자 상태입니다.양자 상태는 이러한 각 특성에 번호를 부여하여 설명할 수 있습니다. 이것들은 전자의 양자 번호로 알려져 있습니다.전자의 양자 상태는 파동 함수에 의해 설명됩니다.파울리 배타 원리는 원자 안에 있는 두 개의 전자가 네 개의 모든 숫자의 동일한 값을 가질 수 없다고 요구합니다.

원자 궤도의 모양.행: 1s, 2p, 3d 및 4f.왼쪽에서 m -,… ,l {\ m=- 색상은 파동 함수의 위상을 나타냅니다.

궤도를 설명하는 첫 번째 특성은 보어의 모델과 동일한 주요 양자 수 n입니다.n은 각 궤도의 에너지 수준을 나타냅니다.n에 대해 가능한 값은 정수입니다.

다음 양자 수, l로 표시된 방위 양자 수는 궤도의 모양을 설명합니다.그 모양은 궤도의 각운동량의 결과입니다.각운동량은 외력의 영향으로 속도가 빨라지거나 느려지는 물체의 저항을 나타냅니다.방위 양자수는 핵 주위에 있는 전자의 궤도 각운동량을 나타냅니다.l에 대한 가능한 값은 0에서 n - 1까지의 정수입니다(여기서 n은 전자의 주요 양자수입니다).

각 궤도의 모양은 보통 방위 양자수가 아닌 문자로 표시됩니다.첫 번째 모양(l=0)은 문자(니모닉은 "구")로 표시됩니다.다음 모양은 문자 p로 표시되며 덤벨의 형태를 가지고 있습니다.다른 궤도는 더 복잡한 모양을 가지고 있으며(원자 궤도 참조), 문자 d, f, g 등으로 표시됩니다.

세 번째 양자수인 자기 양자수는 전자의 자기 모멘트를 나타내며 m(또는 단순히 m)으로l 표시됩니다.m의l 가능한 값은 -l에서 l까지의 정수입니다(여기서 l은 전자의 방위 양자수입니다).

자기 양자수는 특정 방향의 각운동량 성분을 측정합니다.방향 선택은 임의이며, 일반적으로 z 방향이 선택됩니다.

네 번째 양자수인 스핀 양자수(전자 스핀의 "방향"과 관련)는 m으로 표시되며s, 값은 +입니다.1⁄2 또는 -1⁄2.

화학자 리누스 폴링은 예를 들어 다음과 같이 썼습니다.

1s 궤도에 두 개의 전자가 있는 헬륨 원자의 경우, 파울리 배타 원리는 두 개의 전자가 하나의 양자 수의 값에서 서로 다른 것을 요구합니다.n, l 및 m의l 값은 동일합니다.따라서 전자 하나에 +1⁄2, 전자 [61]하나에 -1⁄2의 값을 가질 수 있는 m의 값이 달라야s 합니다."

주기율표의 구성으로 이어지는 것은 원자 궤도의 기본 구조와 대칭, 그리고 전자가 그것들을 채우는 방식입니다.다른 원자들의 원자 궤도가 분자 궤도를 형성하기 위해 결합하는 방법은 원자들 사이의 화학적 결합의 구조와 강도를 결정합니다.

양자 화학 분야는 1927년 수소 분자의 공유 결합에 대한 연구를 발표한 물리학자 월터 하이틀러와 프리츠 런던에 의해 개척되었습니다.양자 화학은 이후 칼텍의 미국인 이론 화학자 리누스 폴링과 존 C를 포함한 많은 노동자들에 의해 개발되었습니다. 나중에 분자 궤도 이론이나 원자가 이론과 같은 다양한 이론으로 넘어가세요.

디랙, 상대성 이론 및 형식 방법의 개발.

1927년경부터 폴 디랙은 전자에 대한 디랙 방정식을 제안함으로써 양자 역학을 특수 상대성 이론과 통합하는 과정을 시작했습니다.디랙 방정식은 슈뢰딩거가 얻지 못한 전자의 파동 함수에 대한 상대론적 설명을 달성합니다.그것은 전자 스핀을 예측하고 디랙이 양전자의 존재를 예측하도록 이끌었습니다.그는 또한 그의 유명한 1930년 교과서에 기술된 것처럼 영향력 있는 브라-켓 표기법을 포함한 연산자 이론의 사용을 개척했습니다.같은 기간 동안 헝가리의 박식가 존 폰 노이만은 그의 유명한 1932년 교과서에서 설명한 것처럼 힐베르트 공간에 대한 선형 연산자 이론으로서 양자 역학에 대한 엄격한 수학적 기초를 공식화했습니다.이것들은 건국 시기의 다른 많은 작품들과 마찬가지로 여전히 남아있고 널리 사용되고 있습니다.

양자장론

1927년 초, 연구원들은 양자 역학을 단일 입자 대신 필드에 적용하려고 시도했고, 그 결과 양자 필드 이론이 만들어졌습니다.이 지역의 초기 노동자들은 P.A.M. 디랙, W. Pauli, V.를 포함합니다. 바이스코프, 그리고 P. 조던.이 연구 분야는 R.P.에 의한 양자 전기 역학의 공식화로 절정에 달했습니다. 파인만, F. 다이슨, J. 슈윙거, 그리고 S. 1940년대의 토모나가.양자전기역학은 전자, 양전자, 전자기장의 양자이론을 설명하며 이후 양자장 [40][41][63]이론의 모델로 사용되었습니다.

양자 색역학에서 글루온 복사의 파인만 다이어그램

양자 색역학 이론은 1960년대 초에 공식화되었습니다.오늘날 우리가 알고 있는 이론은 1975년에 Politzer, Gross 및 Wilchek에 의해 공식화되었습니다.

슈윙거, 힉스, 골드스톤의 선구적인 연구를 바탕으로, 물리학자 글래쇼, 와인버그, 살람은 어떻게 약한 핵력과 양자 전기역학이 하나의 약한 전기약력으로 합쳐질 수 있는지를 독립적으로 보여주었고, 1979년 노벨 물리학상을 받았습니다.

양자 정보

참고 항목:양자 컴퓨팅 및 통신 타임라인

양자 정보 과학은 20세기 후반에 홀보의 정리, 일반화된 측정 또는 POVM의 개념, 베넷과 브라사드에 의한 양자 키 분포의 제안, 쇼어의 알고리즘과 같은 이론적 결과로부터 시작하여 발전했습니다.

기초 실험

참고 항목

레퍼런스

  1. ^ a b c d e f g h i j k l Whittaker, Edmund T. (1989). A history of the theories of aether & electricity. 2: The modern theories, 1900 - 1926 (Repr ed.). New York: Dover Publ. ISBN 978-0-486-26126-3.
  2. ^ Max Born, My Life: 노벨상 수상자의 회상, Taylor & Francis, London, 1978. ("우리는 점점 더 물리학의 기초에 대한 급진적인 변화가 필요하다는 것, 즉 양자 역학이라는 용어를 사용한 새로운 종류의 역학이 필요하다는 것을 확신하게 되었습니다.이 단어는 제 논문에서 물리학 문헌에 처음으로 등장합니다..")
  3. ^ Fedak, William A.; Prentis, Jeffrey J. (2009-02-01). "The 1925 Born and Jordan paper "On quantum mechanics"" (PDF). American Journal of Physics. 77 (2): 128–139. doi:10.1119/1.3009634. ISSN 0002-9505.
  4. ^ Young, Thomas (1804). "Bakerian Lecture: Experiments and calculations relative to physical optics". Philosophical Transactions of the Royal Society. 94: 1–16. Bibcode:1804RSPT...94....1Y. doi:10.1098/rstl.1804.0001. S2CID 110408369.
  5. ^ Buchwald, Jed (1989). The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century. Chicago: University of Chicago Press. ISBN 978-0-226-07886-1. OCLC 18069573.
  6. ^ Feynman, Richard; Leighton, Robert; Sands, Matthew (1964). The Feynman Lectures on Physics. Vol. 1. California Institute of Technology. ISBN 978-0201500646. Retrieved 30 September 2021.
  7. ^ Pojman, Paul (2020), "Ernst Mach", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Winter 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 2021-09-30
  8. ^ 이 결과는 (독일어로) .영어 번역:
  9. ^ "The Nobel Prize in Physics 1918". Nobel Foundation. Retrieved 2009-08-01.
  10. ^ Kragh, Helge (1 December 2000). "Max Planck: the reluctant revolutionary". PhysicsWorld.com. Archived from the original on 1 April 2012. Retrieved 7 December 2009.
  11. ^ Wheaton, Bruce R. (1978). "Philipp Lenard and the Photoelectric Effect, 1889-1911". Historical Studies in the Physical Sciences. 9: 299–322. doi:10.2307/27757381. JSTOR 27757381.
  12. ^ Hawking, Stephen (November 6, 2001) [November 5, 2001]. The Universe in a Nutshell. Vol. 55. Impey, C.D. Bantam Spectra (published April 2002). p. 80~. doi:10.1063/1.1480788. ISBN 978-0553802023. S2CID 120382028. Archived from the original on September 21, 2020. Retrieved December 14, 2020 – via Random House Audiobooks. Alt URL
  13. ^ a b 아인슈타인, 알버트 (1905)."위베레이넨은 에르제우궁과 베르완둥 데 리흐테스는 휴리스틱헨 게시히츠펑크트와 싸웠다."Annalender Physik. 17 (6): 132–48.비브코드:1905AnP...322....132E. doi:10.1002/및 p.19053220607., 2009년 6월 11일 웨이백 머신에서 보관된 빛의 생성과 변환에 관한 발견적 관점으로 영어로 번역됨."광자"라는 용어는 1926년에 도입되었습니다.
  14. ^ Folsing, Albrecht (1997), Albert Einstein: A Biography, trans. Ewald Osers, Viking
  15. ^ Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. pp. 127–29. ISBN 0135897890.
  16. ^ a b Taylor, J. R.; Zafiratos, C. D.; Dubson, M. A. (2004). Modern Physics for Scientists and Engineers. Prentice Hall. pp. 147–48. ISBN 0135897890.
  17. ^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. pp. 70–89, [89]. ISBN 1840465778.
  18. ^ World Book.Inc (2007). "22". World Book Encyclopedia (Electronic reproduction). The World Book encyclopedia. Vol. 22 (3 ed.). Chicago, Illinois: World Book. p. 6. ISBN 978-0716601074. OCLC 894799866. Archived from the original on 30 January 2017. Retrieved December 14, 2020. Alt URL
  19. ^ Wittke, J.P; Dicke, R.H (June 1, 1961) [1960]. "11". In Holladay, W.G. (ed.). Introduction to Quantum Mechanics (eBook). Vol. 16. Nashville, Tennessee: ADDISON WESLEY LONGMAN INC (published January 1, 1978). p. 10. doi:10.1063/1.3057610. ISBN 978-0201015102. OCLC 53473. Retrieved December 14, 2020 – via Vanderbilt University.
  20. ^ Lakhtakia, A (1996). Models and modelers of hydrogen : Thales, Thomson, Rutherford, Bohr, Sommerfeld, Goudsmit, Heisenberg, Schrödinger, Dirac, Sallhofer. Singapore River Edge, NJ: World Scientific. ISBN 981-02-2302-1. OCLC 35643527.
  21. ^ Rutherford, E. (1911). "LXXIX. The scattering of α and β particles by matter and the structure of the atom". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Informa UK Limited. 21 (125): 669–688. doi:10.1080/14786440508637080. ISSN 1941-5982.
  22. ^ 1911년 솔베이 회의의 원래 의사록은 1912년에 출판되었습니다.테오리 뒤 레이온 외 퀀타. 관계자 회의 DELA Réunion tenue a Bruxelles, 1911년 10월 3일, Soules Awarddk M. E. Solvay.출판부 MM. P. 랑주비 등 M. 드 브로글리.프랑스어에서 번역, 447쪽.
  23. ^ a b c Heilbron, John L.; Kuhn, Thomas S. (1969-01-01). "The Genesis of the Bohr Atom". Historical Studies in the Physical Sciences. University of California Press. 1: vi–290. doi:10.2307/27757291. ISSN 0073-2672. JSTOR 27757291.
  24. ^ a b Heilbron, John L. (2013). "The path to the quantum atom". Nature. Springer Science and Business Media LLC. 498 (7452): 27–30. doi:10.1038/498027a. ISSN 0028-0836. S2CID 4355108.
  25. ^ J. W. 니콜슨, 월간지아니, 로이, 아스트소. lxxii. pp. 49,130,677,693,729 (1912).
  26. ^ a b McCormmach, Russell (1966). "The atomic theory of John William Nicholson". Archive for History of Exact Sciences. Springer Science and Business Media LLC. 3 (2): 160–184. doi:10.1007/bf00357268. ISSN 0003-9519. S2CID 120797894.
  27. ^ Nicholson, J. W. (1912-06-14). "The Constitution of the Solar Corona. II". Monthly Notices of the Royal Astronomical Society. Oxford University Press (OUP). 72 (8): 677–693. doi:10.1093/mnras/72.8.677. ISSN 0035-8711.
  28. ^ Nicholson, J. W. (1912). "The Constitution of the Solar Corona. III". Monthly Notices of the Royal Astronomical Society. Oxford University Press (OUP). 72 (9): 729–740. doi:10.1093/mnras/72.9.729. ISSN 0035-8711.
  29. ^ T. 히로시게와 S.니시오, "보어의 원자 헌법 이론의 형성", 일본연구 조직과학, 3번(1964), 6-28;
  30. ^ J. L. Heilbron, 전자의 발견부터 양자 역학의 시작까지 원자 모델의 역사, dis. (캘리포니아 대학교 버클리, 1964).
  31. ^ McCormmach, Russell (Spring 1967), "Henri Poincaré and the Quantum Theory", Isis, 58 (1): 37–55, doi:10.1086/350182, S2CID 120934561
  32. ^ Irons, F. E. (August 2001), "Poincaré's 1911–12 proof of quantum discontinuity interpreted as applying to atoms", American Journal of Physics, 69 (8): 879–84, Bibcode:2001AmJPh..69..879I, doi:10.1119/1.1356056
  33. ^ a b Friedrich, Bretislav; Herschbach, Dudley (December 2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today. 56 (12): 53–59. doi:10.1063/1.1650229. ISSN 0031-9228.
  34. ^ Baggott, J. E. (2013). The quantum story: a history in 40 moments (Impression: 3 ed.). Oxford: Oxford Univ. Press. ISBN 978-0-19-965597-7.
  35. ^ 페이, 에이브러햄"조지 울렌벡과 전자 스핀의 발견."Physics Today 42.12 (1989): 34-40.
  36. ^ Aczel, Amir D., Tanglement, pp. 51ff. (펭귄, 2003) ISBN 978-1551926476
  37. ^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. p. 114. ISBN 1840465778.
  38. ^ McEvoy, J. P.; Zarate, O. (2004). Introducing Quantum Theory. Totem Books. p. 87. ISBN 1840465778.
  39. ^ Navarro, Jaume (2010). "Electron diffraction chez Thomson: early responses to quantum physics in Britain". The British Journal for the History of Science. 43 (2): 245–275. doi:10.1017/S0007087410000026. ISSN 0007-0874.
  40. ^ a b Edwards, David A. (1979). "The mathematical foundations of quantum mechanics". Synthese. Springer Science and Business Media LLC. 42 (1): 1–70. doi:10.1007/bf00413704. ISSN 0039-7857. S2CID 46969028.
  41. ^ a b Edwards, David A. (1981). "Mathematical foundations of quantum field theory: Fermions, gauge fields, and supersymmetry part I: Lattice field theories". International Journal of Theoretical Physics. Springer Science and Business Media LLC. 20 (7): 503–517. Bibcode:1981IJTP...20..503E. doi:10.1007/bf00669437. ISSN 0020-7748. S2CID 120108219.
  42. ^ Hanle, P. A. (December 1977), "Erwin Schrodinger's Reaction to Louis de Broglie's Thesis on the Quantum Theory.", Isis, 68 (4): 606–609, doi:10.1086/351880, S2CID 121913205
  43. ^ Pauli, Wolfgang (1926-05-01). "Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik". Zeitschrift für Physik (in German). 36 (5): 336–363. Bibcode:1926ZPhy...36..336P. doi:10.1007/BF01450175. ISSN 0044-3328. S2CID 128132824.
  44. ^ Mensing, Lucy (1926-11-01). "Die Rotations-Schwingungsbanden nach der Quantenmechanik". Zeitschrift für Physik (in German). 36 (11): 814–823. Bibcode:1926ZPhy...36..814M. doi:10.1007/BF01400216. ISSN 0044-3328. S2CID 123240532.
  45. ^ Van der Waerden, B. L. (1967). Sources of Quantum Mechanics. Mineola, NY: Dover Publications. pp. 261–76. Received 29 July 1925 베르너 하이젠베르크의 논문 "운동학적 및 기계적 관계의 양자-이론적 재해석" 페이지 261–76 참조.
  46. ^ Busch, Paul; Lahti, Pekka; Werner, Reinhard F. (17 October 2013). "Proof of Heisenberg's Error-Disturbance Relation". Physical Review Letters. 111 (16): 160405. arXiv:1306.1565. Bibcode:2013PhRvL.111p0405B. doi:10.1103/PhysRevLett.111.160405. ISSN 0031-9007. PMID 24182239. S2CID 24507489.
  47. ^ Appleby, David Marcus (6 May 2016). "Quantum Errors and Disturbances: Response to Busch, Lahti and Werner". Entropy. 18 (5): 174. arXiv:1602.09002. Bibcode:2016Entrp..18..174A. doi:10.3390/e18050174.
  48. ^ Nobel Prize Organization. "Erwin Schrödinger – Biographical". Retrieved 28 March 2014. His great discovery, Schrödinger's wave equation, was made at the end of this epoch-during the first half of 1926.
  49. ^ 슈뢰딩거 방정식(물리학), 브리태니커 백과사전
  50. ^ Erwin Schrödinger, "양자 역학의 현재 상황", p. 9. "이 번역본은 원래 미국 철학 학회 회의록 124, 323–38에 출판되었고, 그 후 양자 이론 및 측정 (J.A.) 제 1부의 I.11절로 나타났습니다.Wheeler 및 W. H. Zurek, Eds., Princeton University Press, NJ 1983).이 문서는 다음 위치에서 다운로드할 수 있습니다.
  51. ^ 하이젠베르크, W. (1955).양자 이론의 해석의 발전, 닐스 보어의 12-29페이지와 물리학의 발전: 그의 칠순 생일을 맞아 닐스 보어에게 헌정된 에세이들, 폴리, L.와 바이스코프, V. 페르가몬, 런던, 페이지 13: "단일 양자 점프는 본질적으로 "사실적인" 것입니다.
  52. ^ W. 무어, 슈뢰딩거: 삶과 생각, 케임브리지 대학 출판부 (1989), 222페이지슈뢰딩거 자신의 말은 227페이지를 참조하십시오.
  53. ^ Gleick, James (21 October 1986). "Physicists finally get to see quantum jump with own eyes". The New York Times. Retrieved 30 November 2019.
  54. ^ Faye, Jan (2019). "Copenhagen Interpretation of Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
  55. ^ Camilleri, K.; Schlosshauer, M. (2015). "Niels Bohr as Philosopher of Experiment: Does Decoherence Theory Challenge Bohr's Doctrine of Classical Concepts?". Studies in History and Philosophy of Modern Physics. 49: 73–83. arXiv:1502.06547. Bibcode:2015SHPMP..49...73C. doi:10.1016/j.shpsb.2015.01.005. S2CID 27697360.
  56. ^ Omnès, Roland (1999). "The Copenhagen Interpretation". Understanding Quantum Mechanics. Princeton University Press. pp. 41–54. doi:10.2307/j.ctv173f2pm.9. S2CID 203390914.
  57. ^ Scheibe, Erhard (1973). The Logical Analysis of Quantum Mechanics. Pergamon Press. ISBN 9780080171586. OCLC 799397091. [T]here is no point in looking for the Copenhagen interpretation as a unified and consistent logical structure. Terms such as "Copenhagen interpretation" or "Copenhagen school" are based on the history of the development of quantum mechanics; they form a simplified and often convenient way of referring to the ideas of a number of physicists who played an important role in the establishment of quantum mechanics, and who were collaborators of Bohr's at his Institute or took part in the discussions during the crucial years. On closer inspection, one sees quite easily that these ideas are divergent in detail and that in particular the views of Bohr, the spiritual leader of the school, form a separate entity which can now be understood only by a thorough study of as many as possible of the relevant publications by Bohr himself.
  58. ^ Peres, Asher (2002). "Popper's experiment and the Copenhagen interpretation". Studies in History and Philosophy of Modern Physics. 33: 23. arXiv:quant-ph/9910078. Bibcode:1999quant.ph.10078P. doi:10.1016/S1355-2198(01)00034-X. There seem to be at least as many different Copenhagen interpretations as people who use that term; probably there are more.
  59. ^ Mermin, N. David (2017-01-01). "Why QBism Is Not the Copenhagen Interpretation and What John Bell Might Have Thought of It". In Bertlmann, Reinhold; Zeilinger, Anton (eds.). Quantum [Un]Speakables II. The Frontiers Collection. Springer International Publishing. pp. 83–93. arXiv:1409.2454. doi:10.1007/978-3-319-38987-5_4. ISBN 9783319389851. S2CID 118458259.
  60. ^ Bohr, N. (1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0. 보어의 초기 저술 모음집인 원자론과 자연의 설명(1934)에서 이용할 수 있습니다.
  61. ^ a b Pauling, Linus (1960). The Nature of the Chemical Bond (3rd ed.). Itahca, NY: Cornell University Press. p. 47. ISBN 0801403332. Retrieved 1 March 2016.
  62. ^ "궤도 (화학과 물리학), 오비탈
  63. ^ S. Auyang, 어떻게 양자장 이론이 가능할까요?,옥스포드 대학 출판부, 1995.
  64. ^ 전자의 파동성을 보여주는 데이비슨-독일 실험

진일보한 내용

외부 링크

위키 인용문에는 양자역학의 역사와 관련된 인용문이 있습니다.