파동함수

양자 물리학에서 파동함수(또는 파동함수)는 고립된 양자계의 양자 상태를 수학적으로 설명하는 것입니다.파동함수의 가장 일반적인 기호는 $그리스$ 문자 ψ와 ψ(각각 소문자와 대문자 psi)입니다.파동함수는 복소수로 구성되어 있습니다.예를 들어, 파동함수는 공간 영역의 각 점에 복소수를 할당할 수 있습니다.Born 규칙은^[1]^[2]^[3] 이러한 복잡한 확률 진폭을 실제 확률로 변환하는 수단을 제공합니다.한 가지 일반적인 형태에서 위치에 따라 달라지는 파동함수의 제곱 계수는 주어진 위치에 있는 입자를 측정할 확률 밀도라고 말합니다.시스템의 모든 자유도에 대한 파동함수의 제곱 계수의 적분은 정규화라고 불리는 조건인 1과 같아야 합니다.파동함수는 복소값이기 때문에 상대적 위상과 상대적 크기만을 측정할 수 있습니다. 파동함수의 값은 측정 가능한 관측치의 크기나 방향에 대해 어떤 것도 알려주지 않습니다.고유값이 가능한 측정 결과 집합에 해당하는 양자 연산자를 $파동함수$ ψ에 적용하고 측정 가능한 양에 대한 통계적 분포를 계산해야 합니다.

파동함수는 운동량과 같이 위치 이외의 변수의 함수가 될 수 있습니다.위치에 의존하는 파동함수로 표현되는 정보는 푸리에 변환을 통해 운동량에 의존하는 파동함수로 변환될 수 있고, 그 반대의 경우도 가능합니다.전자나 광자와 같은 일부 입자는 0이 아닌 스핀을 가지며, 이러한 입자에 대한 파동함수는 고유한 이산 자유도로서 스핀을 포함하며, 아이소스핀과 같은 다른 이산 변수도 포함할 수 있습니다.시스템에 내부 자유도가 있을 때 연속 자유도의 각 점(예: 공간의 한 점)에서 파동 함수는 이산 자유도의 가능한 각 값(예: 스핀의 z 성분)에 대해 복소수를 할당합니다.이러한 값은 종종 열 행렬(예: 스핀 $1$ ⁄2를 가진 비상대론적 전자에 $대한$ 2 × $1$ 열 벡터)로 표시됩니다.

양자역학의 중첩원리에 따르면 파동함수는 함께 더하고 복소수를 곱하여 새로운 파동함수를 형성하고 힐베르트 공간을 형성할 수 있습니다.두 파동 함수 사이의 내부 생성물은 해당 물리적 상태 사이의 중첩을 측정하는 것으로 전이 확률을 내부 생성물과 관련시키는 양자역학의 기본 확률론적 해석인 Born 규칙에 사용됩니다.슈뢰딩거 방정식은 수학적으로 파동 방정식의 한 종류이기 때문에 시간이 지남에 따라 파동 함수가 어떻게 진화하는지를 결정하고, 파동 함수는 다른 파동처럼 질적으로 행동합니다.이것은 "파동 함수"라는 이름을 설명하고, 파동-입자 이중성을 발생시킵니다.그러나 양자역학의 파동함수는 2023년 현재에도 여전히 다른 해석에 열려 있는 일종의 물리적 현상을 설명하며, 이는 고전적인 기계적 파동과는 근본적으로 다릅니다.^[4]^[5]^[6]^[7]^[8]^[9]^[10]

역사적 배경

In 1900, Max Planck postulated the proportionality between the frequency $f$ of a photon and its energy $E$ , $E=hf$ ,^[11]^[12] and in 1916 the corresponding relation between a photon's momentum $p$ and wavelength $\lambda$ , $\lambda ={\frac {h}{p}}$ $=$ $h$ p {\displaysty $\lambda ={\frac {h}{p}}$ da ={\frac {h}{p}}, 여기서 h {\displaystyle h}는 플랑크 상수입니다.1923년 드브로이는 λ = h p ${\$ displaystyle \ lambda ={\frac {h}{p}} 관계가 현재 드브로이 관계라고 불리는 거대 입자를 보유하고 있으며, 주요 단서는 로렌츠 불변성이며, 이는 양자역학의 현대 발전의 출발점으로 볼 수 있습니다.방정식은 질량이 없는 입자와 질량이 큰 입자 모두에 대한 파동-입자 이중성을 나타냅니다.

1920년대와 1930년대에는 미적분학과 선형 대수학을 사용하여 양자역학이 개발되었습니다.미적분학의 기술을 사용한 사람들은 루이 드 브로이, 에르빈 슈뢰딩거 등이 포함되어 "파동역학"을 개발했습니다.선형대수학의 방법을 적용한 사람들은 베르너 하이젠베르크, 막스 보른 등이 포함되어 "행렬역학"을 개발했습니다.Schrödinger는 이후 두 접근법이 동등하다는 것을 보여주었습니다.^[15]

1926년, 슈뢰딩거는 현재 자신의 이름을 딴 유명한 파동 방정식인 슈뢰딩거 방정식을 발표했습니다.이 방정식은 양자 연산자를 사용한 고전적인 에너지 보존과 드브로이 관계 및 방정식의 해는 양자 시스템에 대한 파동 함수입니다.^[16]하지만, 그것을 어떻게 해석해야 할지에 대해서는 아무도 명확하지 않았습니다.^[17]처음에 슈뢰딩거와 다른 사람들은 파동함수가 대부분의 입자가 파동함수가 큰 곳에 퍼져 있는 입자를 나타낸다고 생각했습니다.^[18]이것은 (입자를 나타내는) 파장 패킷이 표적을 벗어나서 탄성적으로 산란되는 것과 양립할 수 없는 것으로 나타났습니다. 그것은 모든 방향으로 퍼집니다.^[1]산란된 입자는 어느 방향으로든 산란될 수 있지만, 모든 방향으로 분해되어 이륙하지는 않습니다.1926년, Born은 확률 진폭의 관점을 제공했습니다.^[1]^[2]^[19]이것은 양자역학의 계산을 확률적 실험 관측과 직접적으로 연관시킵니다.양자역학에 대한 코펜하겐 해석의 일부로 받아들여지고 있습니다.양자역학에 대한 다른 많은 해석들이 있습니다.1927년, Hartree와 Fock은 N체파 함수를 풀기 위한 첫 번째 시도를 했고, 해를 근사하는 반복 알고리즘인 자기 일관성 주기를 개발했습니다.지금은 하트리로도 알려져 있습니다.가짜 방법.^[20]행렬의 Slater 행렬식과 영구 행렬식은 John C가 제공한 방법의 일부였습니다. 나중에.

슈뢰딩거는 비상대론적인 것을 발표하기 전에 상대론적 에너지 보존을 만족하는 파동함수에 대한 방정식을 만났지만, 음의 확률과 음의 에너지를 예측했기 때문에 그것을 폐기했습니다.1927년 클라인, 고든, 포크도 발견했지만 전자기 상호작용을 통합하여 로렌츠 불변임을 증명했습니다.드브로이 또한 1928년에 같은 방정식에 도착했습니다.이 상대론적 파동 방정식은 현재 클라인-고든 방정식으로 가장 일반적으로 알려져 있습니다.^[21]

1927년 파울리는 현상학적으로 전자기장에서 스핀 1/2 입자를 설명하는 비상대론적 방정식을 발견했는데, 현재는 파울리 방정식이라고 불립니다.^[22]파울리는 파동함수가 공간과 시간의 단일 복소함수에 의해 기술되는 것이 아니라 페르미온의 스핀 +1/2와 -1/2 상태에 각각 해당하는 두 개의 복소수가 필요하다는 것을 발견했습니다.그 직후 1928년에 디랙은 전자에 적용된 특수상대성이론과 양자역학의 첫 번째 성공적인 통일로부터 방정식을 발견했고, 현재는 디랙 방정식이라고 불립니다.여기서 파동함수는 전자에 2개, 전자의 반입자인 양전자에 2개 ^[20]등 4개의 복소값 성분으로 대표되는 스피너입니다.비상대론적 한계에서 디랙 파동함수는 전자에 대한 파울리 파동함수와 유사합니다.나중에 다른 상대론적 파동 방정식들이 발견되었습니다.

현대 이론에서 파동함수와 파동방정식

이 모든 파동 방정식은 지속적으로 중요합니다.슈뢰딩거 방정식과 파울리 방정식은 많은 상황에서 상대론적 변형의 훌륭한 근사치입니다.그들은 상대론적인 문제들보다 실질적인 문제들에서 해결하기가 상당히 쉽습니다.

클라인-고든 방정식과 디랙 방정식은 상대론적이지만 양자역학과 특수 상대성 이론의 완전한 조화를 나타내는 것은 아닙니다.이 방정식들이 슈뢰딩거 방정식과 같은 방식으로 연구되는 양자역학 분야는 매우 성공적이기는 하지만 한계가 있습니다(예: 참조).양고기 이동) 및 개념적 문제(예:디랙 씨).

상대성 이론은 계의 입자 수가 일정하지 않은 것을 필연적으로 만듭니다.완전한 화해를 위해서는 양자장 이론이 필요합니다.^[23]이 이론에서 파동방정식과 파동함수는 그 자리를 갖지만 다소 다른 모습을 하고 있습니다.주요 관심 대상은 파동 함수가 아니라 소위 필드 연산자(또는 "연산자"가 이해되는 필드)로 불리는 힐베르트 상태 공간(다음 섹션에 설명됨)입니다.힐베르트 공간을 구축하기 위해서는 여전히 원래의 상대론적 파동 방정식과 그 해결책이 필요한 것으로 밝혀졌습니다.또한, 자유 필드 연산자, 즉 상호 작용이 존재하지 않는다고 가정할 때 많은 경우 필드(파동 함수)와 동일한 방정식을 (공식적으로) 만족하는 것으로 나타났습니다.

따라서 이와 같이 가장한 클라인-고든 방정식(스핀 $0$ )과 디랙 방정식( $스핀$ $1$ ⁄2)은 이론에 남아 있습니다.더 높은 스핀 유사체에는 Proca 방정식( $스핀$ 1), Rarita-Schwinger $방정식$ ( $스핀$ 3 ⁄2), 그리고 더 일반적으로는 Bargmann-Wigner 방정식이 포함됩니다.질량 없는 자유장의 경우 두 가지 예는 필드 연산자에 대한 자유장 $맥스웰$ 방정식(스핀 1)과 자유장 아인슈타인 방정식( $스핀$ 2)입니다.^[24]이 모든 것은 본질적으로 로렌츠 불변성의 요구에 따른 직접적인 결과입니다.그들의 솔루션은 로런츠 변환 하에서 규정된 방식으로, 즉 로런츠 그룹의 특정 표현 하에서 변환되어야 하며, 다른 합리적인 요구 사항(예: 클러스터 분해 특성)^[25]과 함께 인과 관계에 대한 암시가 있는 방정식을 고정하기에 충분합니다.

이것은 자유장 방정식에 적용됩니다. 교호작용은 포함되지 않습니다.라그랑지안 밀도(상호작용 포함)를 사용할 수 있다면, 라그랑지안 형식주의는 고전적 수준의 운동 방정식을 산출할 것입니다.이 방정식은 매우 복잡하고 해결할 수 없을 수 있습니다.모든 해결책은 고정된 수의 입자를 의미하며 일반적인 "1차 양자화된" 양자 이론처럼 외부 전위가 아닌 입자의 생성 및 소멸을 포함하는 이러한 이론에서 언급된 "상호작용"이라는 용어를 설명하지 않습니다.

끈이론에서 상황은 여전히 유사합니다.예를 들어, 운동량 공간에서의 파동함수는 뚜렷이 정의되지 않은 운동량을 가진 입자(끈)의 일반적인 상태에서 푸리에 팽창 계수의 역할을 합니다.^[26]

정의(한 차원에서 하나의 스핀 없는 입자)

상자 안의 입자에 대한 정상파, 정지 상태의 예.

자유 입자의 이동 파동.

위치파 함수 φ(x)와 운동량파

함수

φ(p)의 실수 부분과 대응하는

확률

밀도

ψ(x)와 ψ ((p)는 하나의 x 또는 p 차원에서

하나

의 스핀-0 입자에

대한

것입니다.입자의 색 불투명도는 위치

x

또는 운동량

p

에서 입자를 찾을 확률 밀도(파동 함수가 아닌)에 해당합니다.

지금은 스핀이 없는 비상대론적 단일 입자의 단순한 경우를 하나의 공간 차원에서 생각해 보세요.보다 일반적인 사례는 아래에서 논의됩니다.

양자역학의 공식에 따르면 $t$ 고정된 $시간$ t{\ $displaystyle$ t $}$ 에서 물리계의 상태는 분리 가능한 복소 힐베르트 공간에 속하는 파동 함수에 의해 주어집니다.^[27]^[28]이와 같이, 두 $파동함수$ ψ와 ψ의 내적은 (t시점에서) 복소수로 정의될 수 있습니다.

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

1

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

ψ

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

2

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

=

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

∞

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

∞

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

1 ∗ (x,

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

t) ψ 2 (x, t)

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

< ∞ {\displaystyle(\Psi_{1},\Psi_

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

2})=\int _{-\infty}^{\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t

(\Psi _{1},\Psi _{2})=\int _{-\infty }^{\infty }\,\Psi _{1}^{*}(x,t)\Psi _{2}(x,t)\,dx<\infty

, dx <\infty }.

자세한 내용은 아래에 나와 있습니다.그러나 파동함수의 내적은 그 자체로 ψ,

(\Psi ,\Psi )=\|\Psi \|^{2}

,

ψ

‖

(\Psi ,\Psi )=\|\Psi \|^{2}

ψ ‖ 2 {\displaystyle (\Psi,\P

(\Psi ,\Psi )=\|\Psi \|^{2}

i )=\\Psi \^{2}},

는 항상 양수의 실수입니다.‖ψ ‖(‖ ‖ $가$ 아님)라는 숫자를 파동 함수 ψ의 표준이라고 합니다.고려되는 분리 가능한 힐베르트 공간은 무한 차원이며,^{[nb 2]} 이는 다양한 조합으로 추가되어 가능한 모든 정사각형 적분 가능 함수를 생성할 수 있는 정사각형 적분 가능 함수의 유한 집합이 없음을 의미합니다.

위치-공간 파동함수

그러한 입자의 상태는 파동함수에 의해 완전히 기술되고,

\Psi (x,t)\...

여기

서 x는 위치이고

t

는 시간입니다.이것은 두 개의 실제 변수

x

와

t

의 복소수 값 함수입니다.

1차원에서 스핀이 없는 입자 하나에 대해, 파동함수를 확률 진폭으로 해석하면, 파동함수의 제곱 계수, 양의 실수

\left \Psi (x,t)\right ^{2}=\Psi ^{*}(x,t)\Psi (x,t)=\rho (x),

는 주어진 시간

t

에서 입자의 위치를 측정하기 위한 확률 밀도로 해석됩니다.별표는 복소 켤레를 나타냅니다.입자의 위치가 측정되면 파동함수로부터 위치를 알 수 없고 확률분포로 설명됩니다.

정규화조건

위치 $x$ 가 간격 $a$ ≤ $x$ ≤ $b일$ 확률은 이 간격에 대한 밀도의 적분입니다.

P_{a\leq x\leq b}(t)=\int _{a}^{b}\, \Psi (x,t) ^{2}dx

여기

서 t는 입자를 측정한 시간입니다.이로 인해 정규화 상태가 발생합니다.

\int _{-\infty }^{\infty }\, \Psi (x,t) ^{2}dx=1\,,

왜냐하면 입자가 측정되면 어딘가에 있을 확률이 100%이기 때문입니다.

주어진 시스템에 대해 모든 가능한 정규화 가능한 파동 함수의 집합은 추상적인 수학적 벡터 공간을 형성하며, 이는 서로 다른 파동 함수를 합하고 복소수에 의해 파동 함수를 곱하는 것이 가능하다는 것을 의미합니다.기술적으로 파동함수는 일반적인 벡터 공간이 아닌 투영된 힐베르트 공간에서 광선을 형성합니다.

벡터로서의 양자 상태

특정한 순간에 파동함수ψ ψ(x, t)의 모든 값은 벡터의 성분입니다.그 중에는 셀 수 없이 많은 수가 있으며 합을 대신하여 적분이 사용됩니다.브라켓 표기법에서 이 벡터는

\Psi (t)\rangle =\int \Psi (x,t) x\rangle dx

그리고 "quantum 상태 벡터" 또는 간단히 "quantum 상태"라고 합니다.추상 벡터 공간의 요소를 나타내는 파동 함수를 이해하는 데에는 다음과 같은 몇 가지 이점이 있습니다.

선형 대수학의 모든 강력한 도구는 파동함수를 조작하고 이해하는 데 사용될 수 있습니다.예:
- 선형대수학은 벡터 공간에 기초가 주어질 수 있는 방법을 설명하고 벡터 공간에 있는 모든 벡터는 이 기초로 표현될 수 있습니다.이것은 위치 공간의 파동 함수와 운동량 공간의 파동 함수 사이의 관계를 설명하고 다른 가능성도 있음을 시사합니다.
- 브라켓 표기법을 사용하여 파동함수를 조작할 수 있습니다.
양자 상태가 추상 벡터 공간의 벡터라는 생각은 양자역학과 양자장 이론의 모든 측면에서 완전히 일반적인 반면, 양자 상태가 공간의 복소 값 "파" 함수라는 생각은 특정 상황에서만 사실입니다.

시간 매개 변수는 종종 억제되며 다음과 같습니다. $x$ 좌표는 연속 지수입니다. $x$ ⟩는 부적절한 벡터라고 불리는데, 이 벡터는 통일성으로 정규화할 수 있는 고유 벡터와는 달리 디랙 델타 함수로만 정규화할 수 있습니다.

\langle x' x\rangle =\delta (x'-x)

따라서

\langlex' \Psi \rangle =\int \Psi (x)\langlex' x\rangle dx=\Psi (x')

그리고.

\Psi \rangle =\int x\rangle \ langlex \Psi \rangle dx=\left(\int x\rangle \ langlex dx\right) \Psi \rangle

아이덴티티 연산자를 조명하는 것입니다.

I=\int x\rangle \ lang x dx\,

이는 N차원 힐베르트 공간에서의 정칙 기저의 완전성 관계와 유사합니다.

기저에서 아이덴티티 연산자를 찾는 것은 추상적 상태를 기저에서 명시적으로 표현할 수 있게 해주며, 그 이상(두 상태 벡터 사이의 내적, 관찰 가능한 다른 연산자는 기저에서 표현될 수 있습니다).

운동량-공간파동함수

입자는 운동량 공간에서도 파동함수를 갖습니다.

\Phi(p,t)

여기

서 p는 - ∞에서 + ∞까지의 임의의 값이 될 수 있는 1차원 운동량이고, t는 시간입니다.

위치의 경우와 유사하게 두 파동함수φ(p, t)와φ(p, t)의 내적은 다음과 같이 정의할 수 있습니다.

(\Phi _{1},\Phi _{2})=\int _{-\infty }^{\infty }\,\Phi _{1}^{*}(p,t)\Phi_{2}(p,t)dp\,

시간에 독립적인 슈뢰딩거 방정식의 한 가지 특정한 해는

\Psi _{p}(x)=e^{ipx/\hbar },

평면파는 운동량 연산자의 고유함수이기

때문

에 운동량이 정확히 p인 입자의 설명에 사용될 수 있습니다.이 함수들은 통일성으로 정규화할 수 없으므로(정사각형 적분이 아님), 물리적 힐베르트 공간의 요소가 아닙니다.세트가.

\{\Psi _{p}(x,t),-\infty \leq p\leq \infty \

모멘텀 기반이라고 불리는 것을 형성합니다.이 "근거"는 일반적인 수학적 의미에서의 근거가 아닙니다.우선, 함수들이 정규화될 수 없기 때문에, 대신 델타 함수로 정규화됩니다.^{[nb 4]}

{\displaystyle(\Psi _{p},\Psi _{p'})=\delta(p-p')}

또 다른 이유로, 그들은 선형적으로 독립적이지만 물리적 힐베르트 공간에 대한 기초로 너무 많은 그들(그들은 셀 수 없는 집합을 형성한다)이 있습니다.다음과 같이 푸리에 변환을 사용하여 모든 함수를 표현하는 데 사용할 수 있습니다.

위치와 운동량 표현 사이의 관계

$x$ 와 p 표현은

{\begin{aligned} \Psi \rangle = I \Psi \rangle &=\int x\rangle \ lang x \Psi \rangle dx=\int \Psi (x) x\rangle dx,\\Psi \rangle = I \Psi \rangle &=\int p\rangle \lang p \Psi \rangle dp=\int \Phi (p) p\rangle dp.\end{align}}

이제 두 방정식의 마지막 표현식을 사용하여 운동량 고유함수에 대한 $상태$ ψ의 투영을 수행합니다.

\int \Psi (x)\lang p\rangle dx=\int \Phi (p')\lang p'\rangle dp'=\int \Phi (p')\delta (p-p')dp'=\Phi (p)

그런 다음 자유 슈뢰딩거 방정식의 위치 표현 해에서 적절하게 정규화된 운동량 고유 상태에 대한 알려진 표현식을 활용합니다.

\langle x p\rangle =p(x)={\frac {1}{\sqrt {2\pi \hbar }}}e^{{\frac {i}{\hbar }}px}\Rightarrow \langle p x\rangle ={\frac {1}{\sqrt {2\pi \hbar }}}e^{-{\frac {i}{\hbar }}px},

손에 쥐다

\Phi (p)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Psi (x)e^{-{\frac {i}{\hbar }}px}dx\,.

마찬가지로, 위치의 고유 함수를 사용하여,

\Psi (x)={\frac {1}{\sqrt {2\pi \hbar }}}\int \Phi (p)e^{{\frac {i}{\hbar }}px}dp\,.

따라서 위치 공간 및 운동량 공간 파동 함수는 서로 푸리에 변환된 것으로 확인됩니다.^[30]동일한 정보를 포함하는 동일한 상태에 대한 두 가지 표현이며 둘 중 하나는 입자의 특성을 계산하기에 충분합니다.

실제로는 위치 공간 파동 함수가 운동량 공간 파동 함수보다 훨씬 더 자주 사용됩니다.관련 식에 들어가는 포텐셜(Schrödinger, Dirac 등)은 어느 근거에서 설명이 가장 쉬운지를 결정합니다.고조파 발진기의 경우 $x$ 와 $penter$ 가 대칭적으로 입력되므로 어떤 설명을 사용하는지는 중요하지 않습니다.동일한 방정식(모듈로 상수)이 생성됩니다.이로부터 조금만 생각해 보면 조화 발진기의 파동 방정식에 대한 해는 $L$ 의² 푸리에 변환의 고유 함수라는 것을 알 수 있습니다.^{[nb 5]}

정의(기타의 경우)

다음은 더 높은 차원과 더 많은 입자를 가진 시스템에 대한 일반적인 파동 함수의 형태이며, 위치 좌표나 운동량 성분보다 다른 자유도를 포함합니다.

유한 차원 힐베르트 공간

힐베르트 공간은 원래 무한 차원의 완전한 내적 공간을 의미하지만, 정의에 따라 유한 차원의 완전한 내적 공간도 포함합니다.^[31]물리학에서는 이들을 종종 유한 차원 힐베르트 공간이라고 부릅니다.^[32]모든 유한 차원 힐베르트 공간에 대하여 전체 힐베르트 공간에 걸쳐 있는 직교 기저 집합이 존재합니다.

N차원 집합 ${\textstyle \{|\phi _{i}\rangle \}}$ { ${\textstyle \{|\phi _{i}\rangle \}}$ ϕ ${\textstyle \{|\phi _{i}\rangle \}}$ i ⟩ } {\ $textstyle$ \{ \ $phi$ _{i}\rangle \} 가 정규일 경우, 이들 상태에 걸쳐 있는 공간에 대한 사영 연산자는 다음과 같이 주어집니다.

P=\sum_{i} \phi_{i}\rangle \lang \phi_{i} = I

여기서

{\textstyle \{|\phi _{i}\rangle \}}

은 { ⟩ i

{\textstyle \{|\phi _{i}\rangle \}}

ϕ}

{\textstyle \{

\phi _{i}\rangle \}이 전체 힐베르트 공간에 걸쳐 있으므로 동일성 연산자와 동일합니다. 따라서 힐베르트 공간의 벡터는 변경되지 않습니다.이는 유한 차원 힐베르트 공간의 완전성 관계로도 알려져 있습니다.

대신 파동 기능은 다음과 같이 제공됩니다.

\psi \rangle = I \psi \rangle =\sum _{i} \phi _{i}\rangle \lang \phi _{i} \psi \rangle

여기서

{\textstyle \{\langle \phi _{i}|\psi \rangle \}}

{⟨ ϕ i ψ ⟩ } {\textstyle \{\lang \phi _{i} \psi \rangle \}는 위의 공식을 사용하여 파동함수를 구성하는 데 사용할 수 있는 복소수의 집합입니다.

내적의 확률해석

집합 ${\textstyle \{|\phi _{i}\rangle \}}$ { ${\textstyle \{|\phi _{i}\rangle \}}$ ϕ ${\textstyle \{|\phi _{i}\rangle \}}$ i ⟩ $}$ {\ $textstyle$ \{ \phi _{i}\rangle \}가 $고유값$ λ $i {\$ textstyle \lambda _{i}인 비퇴화 관측 가능한 고유켓이라면, 양자역학의 가정에 의해 관측 가능한 값이 λ i {\textstyle \lambda _{i}일 확률은 다음과 같습니다.

P_{\psi}(\lambda _{i})= \lang \phi _{i} \psi \rangle ^{2}

일부 관측 가능한 고유값 ${\textstyle \{|\phi _{i}\rangle \}}$ λ {\ $textstyle$ ${\textstyle \{|\lambda ^{(j)}\rangle \}}$ \{ \ $phi$ _{i}\rangle \}의 경우, 만약 고유값 λ {\textstyle \lambda }가 {⟩ (j) ⟩ } {\textstyle \{ \lambda ^{(j)}\rangle \}로 라벨이 붙은 고유 벡터의 부분 집합을 가지면, 양자역학의 가정에 의해,관측 가능한 값을 ${\textstyle \lambda _{i}}$ λ i로 측정할 확률은 $다음$ 과 같습니다. {\ $textstyle$ \lambda _{i}}:

P_{\psi}(\lambda)=\sum_{j} \lang \lambda ^{(j)} \psi \rangle ^{2}= {\widehat {P}_{\lambda } \psi \rangle ^{2}

여기서

{\textstyle {\widehat {P}}_{\lambda }=\sum _{j}|\lambda ^{(j)}\rangle \langle \lambda ^{(j)}|}

λ =

{\textstyle {\widehat {P}}_{\lambda }=\sum _{j}|\lambda ^{(j)}\rangle \langle \lambda ^{(j)}|}

∑

{\textstyle {\widehat {P}}_{\lambda }=\sum _{j}|\lambda ^{(j)}\rangle \langle \lambda ^{(j)}|}

j λ (j) ⟩ ⟨ λ (j) {\textstyle {\widehat {P}_{\lambda} =\sum_{j} \lambda ^{(j)}\rangle \lang^{(j)}\rangle \lambda }는 {⟩ (j) λ} {\textstyle \{(j)}\rangle \}에 걸쳐 있는 부분 공간에 대한 상태의 투영 연산자입니다.

{\textstyle \{|\phi _{i}\rangle \}}

ϕ

{\textstyle \{|\phi _{i}\rangle \}}

i ⟩ } {\textstyle \{ \phi _{i}\rangle \}의 직교 특성으로 인해 등식이 따릅니다.

따라서, 양자 역학 시스템의 상태를 지정하는 ${\textstyle \{\langle \phi _{i}|\psi \rangle \}}$ ${\textstyle |\phi _{i}\rangle }$ ⟨ ϕ ${\textstyle \{\langle \phi _{i}|\psi \rangle \}}$ i ψ ⟩ } {\ $textstyle \phi_$ {i} \psi \rangle \}의 크기는 제곱이 각 ϕ i ⟩ {\textstyle \phi_{i}\rangle} 상태를 측정할 확률을 제공합니다.

상대적 단계의 물리적 의미

두 입자 사이의 상대적인 상만이 간섭을 일으키는 것으로 관찰될 수 있기 때문에 물리적인 중요성을 가지고 있습니다.시스템의 전반적인 단계는 임의적인 것으로 간주됩니다.준비된 상태의 각 상태 ${\textstyle |\phi _{i}\rangle }$ ϕ i ⟩ ${\textstyle$ \phi_{i}\rangle}에 대한 상대적 위상은 준비된 상태의 물리적 의미와 그 대칭성을 기반으로 결정할 수 있습니다.예를 들어, z 방향을 따른 스핀 상태의 중첩으로서 x 방향을 따른 스핀 상태의 구성은 서로에 대한 적절한 위상을 제공하는 z 상태를 따라 스핀에 적절한 회전 변환을 적용함으로써 수행될 수 있습니다.

스핀을 포함하는 응용 프로그램

유한 차원 힐베르트 공간의 예는 ${\textstyle 2s+1}$ + ${\textstyle 2s+1}$ ${\textstyle 2s+1}$ 차원 ${\textstyle 2s+1}$ 힐베르트 공간을 형성하는 ${\textstyle s}$ ${\textstyle s}-$ spin ${\textstyle s}$ 입자의 스핀 고유켓을 사용하여 구성할 수 있습니다.그러나 입자의 상태를 완전히 설명하는 일반적인 파동함수는 입자의 위치 또는 운동량과 관련된 힐베르트 공간을 갖는 텐서 곱을 포함하기 때문에 항상 무한 차원의 힐베르트 공간에서 나옵니다.그럼에도 불구하고 유한 차원 힐베르트 공간에 대해 개발된 기법은 독립적으로 처리되거나 텐서 곱의 선형성을 고려하여 처리될 수 있기 때문에 유용합니다.

${\textstyle s}$ ${\textstyle s}$ - 스핀 ${\textstyle s}$ 입자에 대한 스핀 연산자는 ${\textstyle 2s+1}$ + ${\textstyle 2s+1}$ ${\textstyle$ ${\textstyle (2s+1)^{2}}$ ( $2s+1)^{$ $2}$ 개의 ${\textstyle 2s+1}$ 독립적인 스핀 벡터 성분에 작용하는 유한한 ${\textstyle (2s+1)^{2}}$ 행렬로 ${\textstyle (2s+1)^{2}}$ 표현될 수 있기 때문에 일반적으로 행렬/열/행 표기법을 사용하여 스핀 성분을 표시하는 것이 좋습니다.

예를 들어, 각 $s$ ⟩는 일반적으로 열 벡터로 식별됩니다.

s\rangle \leftrightarrow {\begin{bmatrix}1\\0\\vdots \\0\0\end{bmatrix}}\,\quad s-1\rangle \leftrightarrow {\begin{bmatrix}0\1\,\vdots \\0\0\end{bmatrix}\,\ldots \,\quad -(s-1)\rangle \leftrightarrow {\begin{bmatrix}0\0\dots \1\0\end{bmatrix}}\,\quad s-1\end{bmatrix}\,\,\quad -s\rangle \leftright 화살표 {\begin{bmatrix}0\\0\\vdots \\0\1\\end{bmatrix}

그러나 $kets$ ⟩은 열 벡터와 동의어가 아니거나 동일하지 않기 때문에 일반적인 표기법 남용입니다.열 벡터는 단순히 스핀 성분을 표현하는 편리한 방법을 제공합니다.

표기법에 해당하는 z성분 스핀 연산자는 다음과 같이 쓸 수 있습니다.

{\frac {1}{\hbar }}{\hat {S}}_{z}={\begin{bmatrix}s&0&\cdots &0&0\\0&s-1&\cdots &0&0\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\cdots &-(s-1)&0\\0&0&\cdots &0&-s\end{bmatrix}}

z성분 스핀 연산자의 고유 벡터는 위의 열 벡터이며 고유값은 해당 스핀 양자수입니다.

따라서 이와 같은 유한 차원 힐베르트 공간의 벡터는 다음과 같이 표현됩니다.

\phi \rangle ={\ begin{bmatrix}\ langle \phi \rangle \\\\ langle s-1 \phi \rangle \\\\vdots \\\ langle -(s-1) \phi \rangle \\\\end{bmatrix}}={\ begin{bmatrix}\varepsilon_{s}\\\varepsilon_{s-1}\\varepsilon_{s-1}\\\\varepsilon_{s-s}\\end{bmatrix}}

여기서

{\textstyle \{\varepsilon _{i}\}}

{

{\textstyle \{\varepsilon _{i}\}}

ε i}

{\textstyle \{\varepsilon

_{i}\}는 해당 복소수입니다.

스핀과 관련된 다음 논의에서, 완전한 파동 함수는 유한 차원 힐베르트 공간과 이전에 개발된 파동 함수로부터 스핀 상태의 텐서 곱으로 간주됩니다.따라서 이 힐베르트 공간의 기초는 $|\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle |s_{z}\rangle$ $|\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle |s_{z}\rangle$ ⟩ = r ⟩ $|\mathbf {r} ,s_{z}\rangle =|\mathbf {r} \rangle |s_{z}\rangle$ ⟩ ${\displaystyle$ \ $mathbf$ {r}, s_{z}\rangle = \mathbf {r} \rangle s_{z}\rangle }입니다.

3d 위치 공간의 단일 입자 상태

3개의 공간 차원에서 스핀이 없는 단일 입자의 위치-공간 파동 함수는 위의 1개의 공간 차원의 경우와 유사합니다.

\Psi(\mathbf {r},t)

여기서

r

은 3차원 공간에서의 위치 벡터이고,

t

는 시간입니다.항상 그렇듯이

ψ(r, t)는 실제 변수의 복소수 값 함수입니다.디랙 표기법에서 단일 벡터로

\Psi (t)\rangle =\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r},t)\, \mathbf {r} \rangle

내부 제품, 운동량 공간 파동 함수, 푸리에 변환 등에 대한 이전의 모든 언급은 더 높은 차원으로 확장됩니다.

위치 자유도를 무시한 스핀을 가진 입자의 경우 파동함수는 스핀만의 함수입니다(시간은 매개변수).

\xi(s_{z},t)

여기

서_z s는

z축

을 따른 스핀 프로젝션 양자수입니다.(

z축

은 임의의 선택이며, 파형 함수를 적절하게 변환할 경우 다른 축을 대신 사용할 수 있습니다. 아래를 참조하십시오.)

s z

모수는 r과

t

와는 달리 이산형 변수입니다.예를 들어 스핀-1/2 입자의 경우

s

는_z

+1/2

또는

-1/2만

될 수 있고 다른 값은 될 수 없습니다.(일반적으로

스핀

의 경우

s

는_z

s, s

- 1,

..., -s

+ 1,

-s

가 될 수 있습니다).각각의 양자수를 삽입하면 공간과 시간의 복잡한 가치 함수를 얻을 수 있으며, 그 중

2개

+

1개

가 있습니다.이것들은 열 벡터로 배열될 수 있습니다.

\xi ={\begin{bmatrix}\xi (s,t)\\\xi (s-1,t)\\\vdots \\\xi (-(s-1),t)\\\xi (-s,t)\\\end{bmatrix}}=\xi (s,t){\begin{bmatrix}1\\0\\\vdots \\0\\0\\\end{bmatrix}}+\xi (s-1,t){\begin{bmatrix}0\\1\\\vdots \\0\\0\\\end{bmatrix}}+\cdots +\xi (-(s-1),t){\begin{bmatrix}0\\0\\\vdots \\1\\0\\\end{bmatrix}}+\xi (-s,t){\begin{bmatrix}0\\0\\\vdots \\0\\1\\\end{bmatrix}}

브라켓 표기법에서는 벡터의 성분으로 쉽게 정렬할 수 있습니다.

\xi (t)\rangle =\sum _{s_{z}=-s}^{s}\xi (s_{z},t)\, s_{z}\rangle

전체 $벡터$ ξ은 (적절한 해밀턴이 있는) 슈뢰딩거 방정식의 솔루션으로, $솔루션$ ξ( $s,$ t), ξ $($ s - 1, t), ..., ξ(-s, t)가 있는 2s + 1 일반 미분 $방정식$ 의 결합 $시스템으로$ 펼쳐집니다.일부 저자들은 "파동 함수" 대신 "스핀 함수"라는 용어를 사용합니다.이는 슈뢰딩거 방정식이 파동 방정식의 형태를 취하기 때문에 위치 좌표가 연속 자유도인 위치 공간 파동 함수에 대한 솔루션과 대조됩니다.

더 일반적으로 스핀이 있는 3d 입자의 경우 파동함수는 "위치-스핀 공간"에 다음과 같이 기록될 수 있습니다.

\Psi(\mathbf {r},s_{z},t)

그리고 이것들은 또한 열 벡터로 배열될 수 있습니다.

\Psi (\mathbf {r} ,t)={\begin{bmatrix}\Psi (\mathbf {r} ,s,t)\\\Psi (\mathbf {r} ,s-1,t)\\\vdots \\\Psi (\mathbf {r} ,-(s-1),t)\\\Psi (\mathbf {r} ,-s,t)\\\end{bmatrix}}

스핀 의존성이 항목을 색인화하는 데 위치하고 파동 함수는 공간과 시간의 복잡한 벡터 값 함수입니다.

이산형 변수뿐만 아니라 연속형 변수에 대한 파동 함수의 모든 값이 단일 벡터로 수집됩니다.

\Psi (t)\rangle =\sum _{s_{z}}\int d^{3}\!\mathbf {r} \,\Psi (\mathbf {r} ,s_{z},t)\, \mathbf {r} ,s_{z}\rangle

단일 입자의 경우 위치 상태 $벡터$ ψ⟩와 스핀상태 벡터 ξ⟩의 텐서 곱 ⊗은 복합 위치-스핀 상태 벡터를 제공합니다.

\psi(t)\rangle \!\otimes \! \xi(t)\rangle =\s_{z}}\int d^{3}\!\mathbf {r} \,\psi(\mathbf {r},t)\,\xi(s_{z},t)\,\mathbf {r} \rangle \!\otimes \! s_{z}\rangle

신원을 알 수 있는

\Psi(t)\rangle = \psi(t)\rangle \!\otimes \! \xi(t)\rangle

\Psi(\mathbf {r},s_{z},t)=\psi(\mathbf {r},t)\,\xi(s_{z},t)

\mathbf {r},s_{z}\rangle = \mathbf {r} \rangle \!\otimes \! s_{z}\rangle

시스템의 역학의 기초가 되는 해밀턴 연산자에서 입자의 오비탈과 스핀 각운동량이 분리될 수 있다면 에너지 고유 상태의 텐서 곱 인수분해는 항상 가능합니다(즉, 해밀턴 연산자는 오비탈과 스핀 항의^[34] 합으로 분할될 수 있습니다).시간 의존성은 두 요인 중 하나에 배치될 수 있으며, 각각의 시간 진화를 개별적으로 연구할 수 있습니다.이러한 해밀토니안 하에서, 임의의 텐서 곱 상태는 다른 텐서 곱 상태로 진화하며, 이는 본질적으로 임의의 얽히지 않은 상태가 시간 진화 하에서 얽히지 않은 상태로 유지됨을 의미합니다.이것은 텐서 곱의 상태들 사이에 물리적 상호작용이 없을 때 발생한다고 합니다.분리할 수 없는 해밀턴의 경우 에너지 고유 상태는 인수분해할 필요가 없는 그러한 상태의 선형 조합이라고 합니다. 예를 들어 자기장의 입자, 스핀-궤도 결합 등이 있습니다.

앞의 논의는 불연속적인 변수로서 스핀에 국한되지 않으며, 총 각운동량 J도 사용될 수 있습니다.^[35]아이소스핀과 같은 다른 이산 자유도는 위의 스핀의 경우와 유사하게 표현될 수 있습니다.

3d 위치 공간의 다입자 상태

입자가 많은 경우 일반적으로 각 입자에 대한 별도의 파동함수가 아닌 하나의 파동함수만 존재합니다.양자 얽힘과 EPR 역설을 가능하게 하는 것은 하나의 파동함수가 많은 입자를 기술한다는 사실 때문입니다. $N$ 입자에 대한 위치 공간 파동 함수는 다음과 같이 기록됩니다.^[20]

\Psi(\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},t)

여기

서_i r은 3차원 공간에서 i번째 입자의 위치이고,

t

는 시간입니다.이를 종합하면,

이

는

3N

+ 1개의 실제 변수의 복소수 값 함수입니다.

양자역학에서 동일한 입자와 구별 가능한 입자 사이에는 근본적인 차이가 있습니다.예를 들어, 어떤 두 개의 전자는 동일하고 근본적으로 서로 구별할 수 없습니다. 물리 법칙은 특정 전자를 추적하기 위해 특정 전자에 "식별 번호"를 찍는 것을 불가능하게 만듭니다.^[30]이는 동일한 입자를 가진 시스템에 대한 파동 함수에 대한 요구 사항으로 해석됩니다.

\Psi \left(\ldots \mathbf {r} _{a},\ldots,\mathbf {r} _{b},\ldots \right)=\pm \Psi \left(\ldots \mathbf {r} _{b},\ldots,\mathbf {r} _{a},\ldots \right)

여기서 입자가 모두 보손이면

+부호가 발생하고 모두 페르미온이면

-부호가 발생합니다.즉, 파동함수는 보손의 위치에서 완전히 대칭이거나 페르미온의 위치에서 완전히 반대칭입니다.^[36]입자의 물리적 교환은 파동함수에서 수학적으로 전환되는 인수에 해당합니다.페르미온 파동함수의 반대칭성 특징은 파울리 원리로 이어집니다.일반적으로 보손 및 페르미온 대칭 요구 사항은 입자 통계의 표현이며 다른 양자 상태 형식에 존재합니다.

N개의 $구별$ 가능한 입자(동일한 두 개가 없음, 즉 동일한 양자수 집합을 가진 두 개 없음)의 경우 파동 함수가 대칭 또는 반대 대칭일 필요가 없습니다.

어떤 $것$ 은₁ $좌표 2 2$ r $,$ r, ...와 같고, 다른 것들은 $구별$ 할₁ 수 있습니다. (앞에서 언급한 동일한 입자와 동일하지 않고) 파동함수는 동일한 입자 좌표 $r$ 에서만_i 대칭 또는 반대칭입니다.

\Psi \left(\dots \mathbf {r} _{a},\dots,\mathbf {r} _{b},\dots,\mathbf {x} _{1},\mathbf {x} _{2},\dots \right)=\pm \Psi \left(\dots \mathbf {r} _{b},\dots,\mathbf {r} _{a},\dots,\mathbf {x} _{2},\dots \right)

다시 말하지만, 구별 가능한 입자 좌표 $x$ 에_i 대한 대칭 요구 사항은 없습니다.

각각 스핀을 가진 N개의 입자에 대한 파동함수는 복소값 함수입니다.

\Psi (\mathbf {r} _{1},\mathbf {r} _{2}\cdots \mathbf {r} _{N},s_{z\,1},s_{z\,2}\cdots s_{z\,N},t)

이 모든 성분들을 하나의 벡터로 축적하면

\Psi \rangle =\overbrace {\s_{z\,1},\ldots,s_{z\,N}}^{\text{discrete라벨}}\overbrace {\int_{R_{N}}d^{3}\mathbf{r}_{N}\cdots \int_{R_{1}d^{3}\mathbf{r}_{1}^{\text{continu라벨}\;\underbrace{\Psi}(\mathbf{r}_{1},\ldots,\mathbf{r}_{N},s_{z\,1},\ldots,s_{z\,\ldots\,\,N})}_{\begin{array}{c}{\text{wave 함수(}의 구성 요소)\\{\text{state vector long basis state)}}\end{array}}\;\underbrace {\mathbf {r} _{1},\ldots,\ldots,\ldots,s_{z\,1},\ldots,s_{z\,N}\rangle }_{\text{basis state(베이스)}\,

동일한 입자의 경우, 대칭 요건은 파동 함수의 위치 인수와 스핀 인수 모두에 적용되므로 전체적으로 올바른 대칭을 갖습니다.

내부 생성물의 공식은 모든 좌표 또는 운동량에 대한 적분이며 모든 스핀 양자수에 대한 합입니다.3-d에서 스핀을 갖는 N개 $입자$ 의 일반적인 경우,

(\Psi _{1},\Psi _{2})=\sum _{s_{z\,N}\cdots \sum _{s_{z\,2}}\sum _{z\,1}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r}_{1}\int \limits _{\mathrm {all\,space} }d^{3}\mathbf {r}\cdots \int limits _{\mathrm {all\,space} }d^{3}\mathbf {r}_{N}\Psi _{1}^{*}\left(\mathbf {r}\cdots \mathbf {r}_{N},s_{z\,1}\cdots s_{z\,N},t\right)\Psi _{2}\left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)

이것은 모두

N개

의 3차원 부피 적분과 스핀에 대한

N개

의 합입니다.차동 볼륨 요소(

dr 3 i

)에는_i "dV"

또는 i

"

dxdy i dz i

"라고 쓰여 있습니다.

위치 또는 위치-스핀 공간파 함수의 다차원 푸리에 변환은 운동량 또는 운동량-스핀 공간파 함수를 산출합니다.

확률해석

일반적으로 3d에 스핀이 있는 $N개$ 의 $입자$ 의 경우, ψ을 확률 진폭으로 해석하면 확률밀도는

\rho \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)=\left \Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},s_{z\,1}\cdots s_{z\,N},t\right)\right ^{2}

그리고 시간 t에서 입자 1이 $스핀$ = $m$ 인 영역 $R$ 에 있고 입자 2가 스핀 = m인 영역 R에 있을 확률은 이러한 영역에 대한 확률 밀도의 적분이며 다음 스핀 수에서 평가됩니다.

P_{\mathbf {r} _{1}\in R_{1},s_{z\,1}=m_{1},\ldots ,\mathbf {r} _{N}\in R_{N},s_{z\,N}=m_{N}}(t)=\int _{R_{1}}d^{3}\mathbf {r} _{1}\int _{R_{2}}d^{3}\mathbf {r} _{2}\cdots \int _{R_{N}}d^{3}\mathbf {r} _{N}\left \Psi \left(\mathbf {r} _{1}\cdots \mathbf {r} _{N},m_{1}\cdots m_{N},t\right)\right ^{2}

위상의 물리적 의미

비상대론적 양자역학에서 슈뢰딩거의 시간 의존 파동 방정식을 사용하면 다음과 같은 방정식을 얻을 수 있습니다.

{\frac {\partial \rho}{\partial t}}+\nabla \cdot \mathbf {J} =0

is satisfied, where

{\textstyle \rho (\mathbf {x} ,t)= \psi (\mathbf {x} ,t) ^{2}}

is the probability density and

{\textstyle \mathbf {J} (\mathbf {x} ,

t)=

{\

frac {i\hbar }{2m}}(\psi ^{*}\nabla

\

psi

-\nabla \

psi

^{*})

=

{\frac {\hbar }{m}{\text{Im}}(\psi ^{*}\nabla \

psi

)}는 위의 방정식의 연속 방정식 형태에 따른 확률 플럭스로 알려져 있습니다.

파형 함수에 대해 다음 식을 사용합니다.

\psi(\mathbf {x},t)={\sqrt {\rho(\mathbf {x},t)}\exp {\frac {iS(\mathbf {x},t)}{\hbar}

여기서

{\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}

ρ

{\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}

(x, t) =

{\textstyle \rho (\mathbf {x} ,t)=|\psi (\mathbf {x} ,t)|^{2}}

ψ (x, t) 2

{\textstyle \rho(\

mathbf {x}, t) = \psi(\mathbf {x}, t) ^{2}}는 확률 밀도이고 S (x, t) {\textstyle S(\mathbf {x}, t)}는 파동 함수의 위상입니다.

\mathbf {J}(\mathbf {x},t)={\frac {\rho \nabla S}{m}

따라서 위상의 공간적 변화는 확률 플럭스를 특징짓습니다.

고전적 유추에서, ${\textstyle \mathbf {J} =\rho \mathbf {v} }$ = ρ v {\textstyle \mathbf {J} =\rho \mathbf {v}에 대해, 수량 ∇ Sm {\textstyle {\frac {\nabla S}{m}}는 속도와 유사합니다.불확정성 원리에 따라 속도와 위치를 동시에 결정할 수 없기 때문에 이것이 ${\textstyle {\frac {\nabla S}{m}}}$ 로 ∇ $Sm {\textstyle {\nabla S$ }{m}}를 문자 그대로 해석하는 것을 의미하지는 않습니다.슈뢰딩거의 시간 의존 파동 방정식에 파동함수의 형태를 대입하고 고전적 한계를 취하는 ${\textstyle \hbar |\nabla ^{2}S|\ll |\nabla S|^{2}}$ ℏ ∇ ${\textstyle \hbar |\nabla ^{2}S|\ll |\nabla S|^{2}}$ S ≪ ∇ S $2 {\textstyle$ \ $hbar \nabla$ ^{2}S $\ll$ S ^{2}}:

{\frac {1}{2m}}\nabla S(\mathbf {x},t) ^{2}+V(\mathbf {x})+{\frac {\partial S}{\partial t}=0

그것은 고전역학의 해밀턴-자코비 방정식과 유사합니다. ${\textstyle \mathbf {P} _{\text{class.}}=\nabla S}$ 해석은 P ${\textstyle \mathbf {P} _{\text{class.}}=\nabla S}$ 가 있는 해밀턴-자코비 이론과 일치합니다 ${\textstyle \mathbf {P} _{\text{class.}}=\nabla S}$ $∇$ }} $=$ \ $nabla$ S ${\textstyle \mathbf {P} _{\text{class.}}=\nabla S}$ $여기$ 서 S는 해밀턴의 주함수입니다.

시간 의존성

시간에 독립적인 전위에 있는 시스템의 경우 파동 함수는 항상 자유도에 시간에 의존하는 위상 인자를 곱한 함수로 기록될 수 있으며, 그 형태는 슈뢰딩거 방정식으로 제공됩니다. $N개$ 의 입자에 대해서는 그들의 위치만을 고려하고 다른 자유도를 억제하는 것,

\Psi(\mathbf {r} _{1},\mathbf {r} _{2},\ldots,\mathbf {r} _{N},t)=e^{-iEt/\hbar }\,\psi(\mathbf {r} _{1},\mathbf {r} _{2},\ldots,\mathbf {r} _{N}\,

여기서

E

는

고유

상태 ψ에 해당하는 시스템의 에너지 고유 값입니다.이러한 형태의 파동함수를 정지 상태라고 합니다.

양자 상태와 연산자의 시간 의존성은 연산자와 상태에 대한 단일 변환에 따라 배치될 수 있습니다.임의의 양자 상태ψ ⟩ 및 연산자 O에 대해 슈뢰딩거 그림 ψ(t) ⟩은 O가 일정한 동안 슈뢰딩거 방정식에 따라 시간에 따라 변합니다.Heisenberg 사진에서 그것은 반대 방향이며,ψ ⟩은 일정하고, O(t)는 $Heisenberg$ 운동 방정식에 따라 시간에 따라 진화합니다.디랙(또는 상호작용) 그림은 중간이고, 시간 의존성은 운동 방정식에 따라 진화하는 연산자와 상태 모두에 위치합니다.주로 S-매트릭스 요소를 계산하는 데 유용합니다.^[38]

비상대론적 예

다음은 하나의 비상대론적 스핀 없는 입자에 대한 슈뢰딩거 방정식의 해입니다.

유한 퍼텐셜 장벽

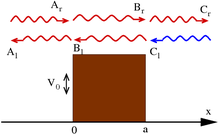
파동역학의 가장 두드러진 특징 중 하나는 입자가 (고전역학에서) 엄청난 힘의 전위를 가진 위치에 도달할 가능성입니다.일반적인 모델은 "잠재적 장벽"이고, 1차원 케이스는 잠재적인 장벽을 가지고 있습니다.

V(x)={\begin{case}V_{0}& x <a\\0& x \geq a\end{cases}}

그리고 파동 방정식에 대한 정상 상태 해는 (일부 상수

k

에

대해, κ) 형태를 갖습니다.

\Psi(x)={\begin{case}A_{\mathrm {r} }e^{ikx}+A_{\mathrm {l} }e^{-ikx}&x<-a,\\B_{\mathrm {r} }e^{\kappa x}+B_{\mathrm {l} }e^{-\kappa x}& x \leq a,\\C_{\mathrm {r} }e^{ikx}+C_{\mathrm {l} }e^{-ikx}&x>a.\end{case}}

이러한 파동함수는 정규화되지 않음을 유의하십시오. 논의는 산란 이론을 참조하십시오.

이에 대한 표준적인 해석은 $입자$ 흐름이 왼쪽( $음$ 의 x 방향)에서 계단에서 발사되는 것입니다. A = $1$ 을 설정하면 입자를 발사하는 것과 $일치$ 합니다. $A$ 와 C를 포함하는 용어는 오른쪽으로 움직임을 나타내고 $A$ 와 $C$ 는 왼쪽으로 움직임을 나타냅니다.오른쪽에서 입자가 나오지 않으므로 이 빔 해석 $아래$ 에 C = $0$ 을 넣으십시오.따라서 파동함수와 그 도함수들의 연속성을 경계에 적용함으로써 위의 상수들을 결정할 수 있습니다.

반지름이 엑시톤 보어 반지름보다 작은 반도체 결정체에서는 엑시톤이 비집고 들어가 양자가 구속됩니다.그런 다음 여러 상태의 에너지가 상자의 길이에 따라 달라지는 상자 모델의 입자를 사용하여 에너지 수준을 모델링할 수 있습니다.

양자 고조파 발진기

양자 고조파 진동자에 대한 파동함수는 에르미트 다항식 $H$ 로_n 표현될 수 있습니다.

\Psi _{n}(x)={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot e^{-{\frac {m\omega x^{2}}{2\hbar }}}\cdot H_{n}{\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)}

여기

서 n = 0,

1, 2, ...

수소원자

수소 원자에서 전자의 파동 함수는 구면 조화론과 일반화된 라게르 다항식으로 표현됩니다(이들은 저자에 따라 다르게 정의됩니다(이들과 수소 원자에 대한 주요 기사 참조).

구면좌표를 사용하는 것이 편리하고, 파동함수를 각 좌표의 함수로 분리할 수 있으므로,^[39]

\Psi _{n\ell m}(r,\theta ,\phi )=R(r)\,\,Y_{\ell }^{m}\!(\theta ,\phi )

여기서

R

은 반지름 함수이고

Y (

θ, φ)는

차수

ℓ 및 차수 m의 구면 조화입니다.이것은 슈뢰딩거 방정식이 정확히 풀린 유일한 원자입니다.다중 전자 원자는 대략적인 방법이 필요합니다.솔루션 제품군은 다음과 같습니다.^[40]

\Psi _{n\ell m}(r,\theta,\phi )={\sqrt {\left ({\frac {2}{na_{0}}\right)}^{3}{\frac {(n-\ell -1)!}{2n[(n+\ell!)]}}}}e^{-r/na_{0}}\left({\frac {2r}{na_{0}}}\right)^{\ell }L_{n-\ell -1}^{2\ell +1}\left({\frac {2r}{na_{0}}}\right)\cdot Y_{\ell }^{m}(\theta ,\phi )

여기

서 a = 4 πεħ/me는 보어 반경이고,

L

은

n

- ℓ - 1, n = 1, 2, ...의 일반화된 라게르 다항식이며, ℓ = 0, 1, ..., n - 1은 방위 양자수, m = - ℓ, - ℓ + 1, ..., ℓ - 1은 자기 양자수를 ℓ합니다.수소와 같은 원자는 용액이 매우 비슷합니다.

이 솔루션은 전자의 스핀을 고려하지 않습니다.

수소 궤도의 그림에서 19개의 하위 이미지는 위치 공간에서의 파동 함수(그들의 표준 제곱)의 이미지입니다.파동 함수는 각 이미지의 오른쪽 아래에 있는 양자수 $(n,$ ℓ, m)의 3배로 특징지어지는 추상 상태를 나타냅니다.주양자수, 궤도 각운동량 양자수, 자기양자수입니다.전자의 스핀-프로젝션 양자수 하나와 함께, 이것은 완전한 관측 가능한 집합입니다.

그림은 파동함수의 함수 공간의 몇 가지 추가적인 특성을 설명하는 역할을 할 수 있습니다.

이 경우 파동 함수는 제곱 적분이 가능합니다.처음에는 함수 공간을 일반적으로 $L$ 로² 표시되는 제곱 적분 가능 함수의 공간으로 취할 수 있습니다.
표시된 함수는 슈뢰딩거 방정식의 해입니다. $분명히 2$ , L의 모든 함수가 수소 원자에 대한 슈뢰딩거 방정식을 만족하는 것은 아닙니다.따라서 함수 공간은 $L$ 의² 부분 공간입니다.
표시된 기능은 기능 공간에 대한 기준의 일부를 형성합니다.각 삼중 $(n,$ ℓ, m)에는 기본 파동 함수가 있습니다.스핀을 고려한다면, 각 삼중에 대해 두 개의 기저 함수가 존재합니다.따라서 함수 공간에는 셀 수 있는 기반이 있습니다.
기본 함수는 상호 직교합니다.

파동함수 및 함수공간

함수공간의 개념은 파동함수에 대한 논의에서 자연스럽게 들어갑니다.함수 공간은 일반적으로 함수에 대한 몇 가지 정의 요구 사항을 포함하는 함수 집합이며, 때때로 집합의 대수 구조(현재 경우 내부 곱이 있는 벡터 공간 구조)와 집합의 토폴로지를 포함합니다.후자는 여기서 드문드문 사용될 것이며, 함수 공간의 부분 집합이 닫히는 것이 무엇을 의미하는지에 대한 정확한 정의를 얻기만 하면 됩니다.파동함수의 함수공간은 힐베르트 공간이라는 결론이 아래에서 내려질 것입니다.이 관찰은 양자역학의 지배적인 수학적 공식의 기초입니다.

벡터공간구조

파동함수는 부분적으로 다음과 같은 구체적이고 추상적인 설명을 특징으로 하는 함수 공간의 요소입니다.

슈뢰딩거 방정식은 선형입니다.이는 이에 대한 해결책인 파동 함수를 스칼라에 추가하고 곱하여 새로운 해결책을 형성할 수 있음을 의미합니다.슈뢰딩거 방정식의 해들의 집합은 벡터 공간입니다.
양자역학의 중첩원리.만약 ψ φ와 φ가 $양자역학계$ 의 추상적인 상태 공간에서 두 개의 상태이고, a와 b가 $임의$ 의 두 $복소수$ 라면, A ψ + B φ도 유효한 상태입니다. (null vector가 유효한 상태로 간주되는지 여부("계가 존재하지 않음")는 정의의 문제입니다.null 벡터는 양자장 이론에서 진공 상태를 전혀 설명하지 않습니다.)허용 상태 집합은 벡터 공간입니다.

물론 이러한 유사성은 우연이 아닙니다.염두에 두어야 할 공간 간의 차이도 있습니다.

표현

기본 상태는 양자수의 집합으로 특징지어집니다.이 값은 통근 관측치의 최대 집합의 고유값 집합입니다.물리적 관측치는 벡터 공간에서 관측치라고도 불리는 선형 연산자로 표시됩니다.최대성은 집합에 이미 존재하는 관측치와 통근하는 대수적으로 독립적인 관측치를 더 이상 추가할 수 없음을 의미합니다.이러한 집합의 선택을 표현의 선택이라고 할 수 있습니다.

위치, 운동량 또는 스핀과 같은 물리적으로 관찰 가능한 계의 양이 상태 공간의 선형 에르미트 연산자로 표현된다는 양자역학의 공식입니다.수량 측정의 가능한 결과는 측정 시스템의 고유 값입니다.^[18]더 깊은 수준에서 대부분의 관측치, 아마도 모두 대칭의 생성기로 발생합니다.^[18]^[41]^{[nb 6]}
물리적 해석은 이러한 집합이 이론적으로 임의의 정밀도로 동시에 측정할 수 있는 것을 나타낸다는 것입니다.Heisenberg 불확정성 관계는 두 개의 비통근 관측치의 동시 정확한 측정을 금지합니다.
세트는 독특하지 않습니다.예를 들어, 일입자 시스템에 대해 위치 및 스핀 z-투영, ( $x,$ $S z)$ 또는 운동량 및 스핀-투영, ( $p y,$ S)일 수 있습니다 $.$ 이 경우, 위치에 해당하는 연산자(위치 표현에서의 곱셈 연산자)와 운동량에 해당하는 연산자(위치 표현에서의 미분 연산자)는 통근하지 않습니다.
일단 대표를 선택하면 여전히 임의성이 있습니다.좌표계를 선택해야 합니다.예를 들어, 이는 $x,$ $y축$ 및 z축 중 하나 또는 수소 원자파 기능에 사용되는 구면 좌표로 예시된 곡선 좌표 중 하나에 해당할 수 있습니다.이 최종 선택은 추상 힐베르트 공간에서도 기초를 고정합니다.기본 상태는 통근 관측치의 최대 집합과 적절한 좌표계에 해당하는 양자 번호로 표시됩니다.^{[nb 7]}

추상적인 상태는 특정한 명시적인 설명에 필요한 임의의 선택이 주어지지 않는다는 점에서만 "추상적"입니다.이는 통근 관측치의 최대 집합에 대한 선택권이 주어지지 않았다는 것과 같습니다.이것은 지정된 기저가 없는 벡터 공간과 유사합니다.따라서 상태에 해당하는 파동 함수는 고유하지 않습니다.이러한 비특이성은 통근 관측치의 최대 집합을 선택할 때 비특이성을 반영합니다.한 차원에서 한 스핀 입자의 경우 특정 상태에 대해 두 개의 파동 함수인ψψ(x, S)와p s( $p$ , S)가 모두 동일한 상태를 설명합니다.

추상 상태 공간에 대한 최대 통근 관측치 집합의 각 선택에 대해 파동 함수의 함수 공간과 관련된 해당 표현이 있습니다.
이 모든 다른 함수 공간과 추상 상태 공간 사이에는 일대일 대응(여기서는 정규화 및 관찰할 수 없는 위상 요인을 무시함)이 있으며, 여기서 공통 분모는 특정 추상 상태입니다.예를 들어, 동일한 상태를 설명하는 것은 운동량과 위치 공간파 함수 사이의 관계입니다.

각각의 표현 선택은 그 표현 선택에 해당하는 파동 함수가 살아있는 고유한 함수 공간을 지정하는 것으로 생각되어야 합니다.두 개의 그러한 함수 공간이 수학적으로 동일하다고 주장할 수 있더라도, 예를 들어 제곱 적분 가능 함수의 집합이 되는 것은 이 구별을 가장 잘 유지합니다.그런 다음 기능 공간을 해당 집합의 두 개의 서로 다른 복사본으로 생각할 수 있습니다.

내품

파동함수의 벡터공간과 추상상태공간에는 추가적인 대수적 구조가 있습니다.

물리적으로 서로 다른 파동함수는 어느 정도 중첩되는 것으로 해석됩니다.상태 φ와 겹치지 않는 상태 ψ의 시스템은 측정 시 상태 φ에 $있는$ 것을 확인할 수 없습니다.그러나φ, φ, … ψ이 어느 정도 겹친다면,ψ에 의해 기술된 $시스템$ 의 측정이 φ, φ, …의 주에서 발견될 가능성이 있습니다. 또한 선택 규칙이 적용됩니다.이들은 일반적으로 일부 양자수의 보존에서 공식화됩니다.이는 초기 및 최종 총파 함수가 겹치지 않기 때문에 일부 관점에서 허용되는 특정 프로세스(예: 에너지 및 운동량 보존)가 발생하지 않음을 의미합니다.
수학적으로, 특정 퍼텐셜에 대한 슈뢰딩거 방정식의 해는 어떤 식으로든 직교한다는 것이 밝혀졌는데, 이는 일반적으로 적분으로 설명됩니다. $\int \Psi _{m}^{*}\Psi _{n}w\,dV=\delta _{nm},$ 여기서 $m,$ $n$ 은 (양자수의) 지수 집합으로 서로 다른 해를 표시하고, 엄밀하게 양의 $함수$ w를 가중치 함수라고 $하며$ , δ는 크로네커 델타입니다.통합은 관련 공간을 모두 차지합니다.

이는 추상 양자 상태의 벡터 공간에 내부 제품을 도입하는 동기를 부여하며, 표현으로 전달될 때 위의 수학적 관찰과 호환됩니다.이는(ψ, φ) 또는 브라-켓표기법 ⟨ ψ ⟩로 표시됩니다.복잡한 숫자를 산출합니다.내부 제품과 함께 기능 공간은 내부 제품 공간입니다.내부 제품(일반적으로 적분 또는 적분의 합)의 명시적인 모양은 표현의 선택에 따라 다르지만 복소수 $($ ψ, φ)는 그렇지 않습니다.양자역학의 물리적 해석의 대부분은 Born 규칙에서 비롯됩니다.측정 시 시스템이 ψ 상태에 있는 상태 φ를 발견할 확률 $p$ 는 다음과 같습니다.

p= (\Phi,\Psi ) ^{2

여기서 ψ 및 φ는 정규화된 것으로 가정합니다.산란 실험을 고려해 보십시오.양자장 이론에서

산란

입자 간의 상호 작용이

멈춘

후 φ이 "먼 미래"("out state")의 상태를 설명하고, ψ이 "먼 과거"의 "상태"인 경우, φ과 ψ이 각각 상태와 외부 상태의 완전한 집합에 따라 달라지는

양

(φ, ψ)을 S-행렬 또는 산란 행렬이라고 합니다.그것에 대한 지식은, 적어도 예측에 관한 한, 당면한 이론을 효과적으로 해결한 것입니다.붕괴 속도 및 산란 단면과 같은 측정 가능한 양은 S-매트릭스에서 계산할 수 있습니다.^[42]

힐베르트 공간

위의 관측은 파동 함수가 원소인 함수 공간의 본질을 캡슐화합니다.그러나 설명이 아직 완료되지 않았습니다.함수 공간에 대한 추가적인 기술적 요구 사항이 있는데, 이는 함수 공간의 시퀀스의 한계를 취할 수 있고, 한계가 존재하는 경우 함수 공간의 요소임을 보장할 수 있습니다.완전한 내적 공간을 힐베르트 공간이라고 합니다.완전성의 속성은 양자역학의 고급 치료와 응용에 중요합니다.예를 들어 사영 연산자 또는 직교 사영의 존재는 공간의 완전성에 의존합니다.^[43]이러한 투영 연산자는 차례로 스펙트럼 정리와 같은 많은 유용한 정리의 진술과 증명에 필수적입니다.도입 양자역학에서는 그다지 중요하지 않으며, 다음과 같은 기술적 세부 사항과 링크는 각주에서 찾을 수 있습니다.^{[nb 8]}공간 $L$ 은² 힐베르트 공간으로, 나중에 내적이 제시됩니다.그림의 예제의 $함수공간$ 은² L의 부분공간입니다. 힐베르트 공간의 부분공간은 닫힌 공간이면 힐베르트 공간입니다.

요약하면, 특정 기저 선택을 갖는 시스템에 대해 가능한 모든 정규화 가능한 파동 함수의 집합은 널 벡터와 함께 힐베르트 공간을 구성합니다.

$관심 2$ 있는 모든 함수가 어떤 힐베르트 공간의 요소인 것은 아니라고 L은 말합니다.가장 눈에 띄는 예는 함수 $e$ 의^{2πip · x⁄h} 집합입니다.이것들은 자유 입자에 대한 슈뢰딩거 방정식의 평면파 해이지만 정규화할 수 없으므로 $L$ 에서는² 그렇지 않습니다. 그러나 그럼에도 불구하고 이들은 설명에 기본적입니다.이를 사용하여 웨이브 패킷을 사용하여 정규화 가능한 기능을 표현할 수 있습니다.그것들은 어떤 의미에서 관심 있는 파동 함수가 표현될 수 있는 기저(하지만 힐베르트 공간 기저나 하멜 기저는 아닙니다)입니다.또한 표기법의 편의를 위해 자주 사용되는 "델타 함수로의 정규화"라는 아티팩트도 있습니다. 자세한 내용은 아래를 참조하십시오.델타 함수 자체도 제곱 적분이 불가능합니다.

파동함수를 포함하는 함수공간에 대한 위의 설명은 대부분 수학적 동기에 의한 것입니다.기능 공간은 완전성으로 인해 어떤 의미에서는 매우 큽니다.모든 함수가 어떤 물리적 시스템에 대한 현실적인 설명은 아닙니다.예를 들어, 함수 공간 $L$ 에서는² 모든 유리수에 대해 $0$ 의 값을 갖는 $함수와 [0,$ 1] 구간의 무리수에 대해 $-i$ 를 갖는 함수를 찾을 수 있습니다.이것은 제곱 적분이 ^{[nb 9]}가능하지만 물리적 상태를 거의 나타낼 수 없습니다.

공통 힐베르트 공간

전체적으로 해의 공간은 힐베르트 공간이지만, 성분으로서 흔히 발생하는 다른 많은 힐베르트 공간들이 있습니다.

구간 $[0,$ 2π]에서 제곱 적분 가능한 복소수 값 함수.집합 { $e /2$ π, n ∈ Z}는 힐베르트 공간 기저, 즉 최대 직교 집합입니다.
푸리에 변환은 위 공간의 함수를 제곱합 가능 $함수$ Z→ $C$ 의 $공간$ 인 l $(Z$ )의 원소로 가져갑니다.후자의 공간은 힐베르트 공간이고 푸리에 변환은 힐베르트 공간의 동형입니다.^{[nb 10]}Its basis is ${e i, i \in Z}$ with $e i (j) = δ ij, i, j \in Z$ .
스패닝 다항식의 가장 기본적인 예는 $[-1,$ 1] 구간의 제곱 적분 가능 함수의 공간이며, 여기서 레전드르 다항식은 힐베르트 공간 기저(완전 직교 집합)입니다.
단위 구 $S 2$ 위의 제곱 적분 가능 함수는 힐베르트 공간입니다.이 경우 기본 기능은 구면 고조파입니다.Legendre 다항식은 구면 조화론의 성분입니다.회전 대칭의 대부분의 문제는 그 대칭과 관련하여 "동일한" (알려진) 해를 가질 것이므로 원래의 문제는 더 낮은 차원의 문제로 축소됩니다.
관련된 라게르 다항식은 구형 고조파를 인수분해한 후 수소파 함수 문제에 나타납니다.이들은 반무한 구간 $[0,$ ∞]에서 제곱 적분 가능 함수의 힐베르트 공간에 걸쳐 있습니다.

더 일반적으로, 힐베르트 공간의 설정에서 스투름-류빌 방정식에 대한 모든 2차 다항식 해의 통합 처리를 고려할 수 있습니다.여기에는 레전드르 다항식과 라구에르 다항식뿐만 아니라 체비셰프 다항식, 야코비 다항식, 에르미트 다항식이 포함됩니다.이 모든 것들은 실제로 물리적인 문제에서 나타나고, 후자는 조화 진동기에서 나타나며, 그렇지 않으면 특수 함수의 속성들로 이루어진 당황스러운 미로가 사실의 조직체가 됩니다.이에 대해서는 Byron & Fuller(1992, 5장)를 참조하십시오.

유한 차원 힐베르트 공간도 발생합니다.공간 $C$ 는ⁿ 차원 $n$ 의 힐베르트 공간입니다.내부 제품은 이러한 공간의 표준 내부 제품입니다.그 안에는 단일 입자 파동 함수의 "스핀 부분"이 존재합니다.

전자의 $비$ relat론적 설명에서 전자는 n = 2이고 $전체$ 파동함수는 파울리 방정식의 해입니다.
$해당$ 상대론적 처리에서 n = $4$ 이고 파동함수는 디랙 방정식을 해결합니다.

입자가 많아지면 상황이 더 복잡해집니다.텐서 곱을 사용하고 (전체) 스핀파 함수가 있는 공간을 텐서 곱에서 추출하기 위해 관련된 대칭 그룹(회전 그룹과 로렌츠 그룹)의 표현 이론을 사용해야 합니다. (입자가 자유롭지 않은 한 상대론적인 경우에 추가 문제가 발생합니다.^[44]베테-살피터 방정식을 참조하십시오.)해당 발언은 대칭군이 SU(2)인 아이소스핀의 개념에 적용됩니다.60년대의 핵력 모형은 대칭군 SU(3)를 사용했습니다.이 경우에도 내부 대칭에 해당하는 파동 함수의 부분은 그러한 $공간$ 의ⁿ 텐서 곱의 일부 C 또는 부분 공간에 존재합니다.

양자장 이론에서 기본적인 힐베르트 공간은 포크 공간입니다.그것은 자유로운 단일 입자 상태, 즉 표현이 선택될 때 파동 함수로부터 구축되며, 반드시 시간적으로 일정하지는 않지만 유한한 입자 수를 수용할 수 있습니다.흥미로운(또는 오히려 다루기 쉬운) 역학은 파동 함수가 아니라 포크 공간에 작용하는 연산자인 필드 연산자에 있습니다.따라서 Heisenberg 그림이 가장 일반적인 선택(일정한 상태, 시간 가변 연산자)입니다.

시스템의 무한 차원적 특성으로 인해 기능 분석에서 적절한 수학적 도구는 연구의 대상이 됩니다.

간단한 설명

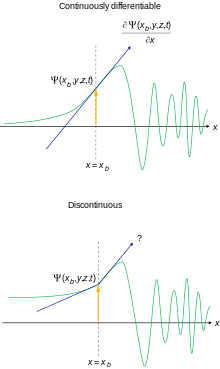
모든 입문 교과서가 긴 경로를 택하여 완전한 힐베르트 공간 기계를 소개하는 것은 아니지만, 특정 표준 퍼텐셜에 대한 위치 표현에서 비상대론적 슈뢰딩거 방정식에 초점을 맞추고 있습니다.파동 함수에 대한 다음의 제약 조건은 때때로 계산과 물리적 해석을 이해하기 위해 명시적으로 공식화됩니다.^[45]^[46]

파동 함수는 제곱 적분이 가능해야 합니다.이것은 파동함수를 확률 진폭으로 해석하는 코펜하겐의 해석에 의해 동기 부여됩니다.
어디에서나 연속적이고 어디에서나 연속적으로 차별화할 수 있어야 합니다.이것은 대부분의 물리적으로 합리적인 전위에 대한 슈뢰딩거 방정식의 출현에 의해 동기 부여됩니다.

특수한 목적을 위해 이러한 조건을 어느 정도 완화하는 것이 가능합니다.^{[nb 11]}이러한 요구 사항이 충족되지 않으면 파동 함수를 확률 진폭으로 해석할 수 없습니다.^[47]퍼텐셜장의 무한 불연속적인 점에서 도함수 규칙의 연속성에 예외가 발생할 수 있습니다.예를 들어, 퍼텐셜이 무한히 불연속적인 것으로 알려진 상자의 경계에서 파동함수의 도함수가 불연속적일 수 있는 상자의 입자에서 말입니다.

이것은 이러한 특정 파동 함수가 거주하는 힐베르트 공간의 구조를 변경하는 것이 아니라, 두 번째 요구 사항을 만족하는 힐베르트 공간인 제곱 적분 함수 $L$ 의² 부분 공간은 $L$ 에서² 닫히지 않으므로, 그 자체로 힐베르트 공간이 아닙니다.^{[nb 12]}요구 사항을 충족하지 못하는 기능은 기술적, 실용적인 이유로 여전히 필요합니다.^{[nb 13]}^{[nb 14]}

파동함수 및 추상상태공간에 관한 더 많은 정보

입증된 바와 같이, 시스템에 대한 일부 표현에서 가능한 모든 파동 함수의 집합은 일반적으로 무한 차원 힐베르트 공간을 구성합니다.표현 기저의 여러 가능한 선택으로 인해 이러한 힐베르트 공간은 고유하지 않습니다.따라서 어떤 사람은 추상적인 힐베르트 공간, 상태 공간에 대해 이야기하고, 거기서 재현과 근거의 선택은 결정되지 않은 채로 남겨집니다.구체적으로 각 상태는 상태 공간에서 추상 벡터로 표현됩니다.^[48]임의의 표현에서 양자 상태ψ ⟩는 일반적으로 벡터로 표현됩니다.

\Psi \rangle =\sum _{\boldsymbol {\alpha}}\int d^{m}\!{\boldsymbol {\omega}}\,\,\Psi({\boldsymbol {\alpha}},{\boldsymbol {\omega}},t)\,{\boldsymbol {\alpha},{\omega}\rangle

어디에

$α, ω$ ⟩ 선택한 표현의 기본 벡터
$d$ $ω =$ $d$ $ω$ d $ω$ ...d $ω$ 연속 자유도에서 "차체 체적 요소"
$ψ($ α, $ω$ , t) 벡터 $ψ$ $⟩$ 의 구성 요소로, 계의 파동 함수라고 합니다.
$α$ $=$ (α, $α, ...,$ $α)$ 무차원 이산 양자수
$ω =$ ( $ω$ , $ω$ , ..., $ω$ ) 연속형 변수(반드시 차원이 없는 것은 아님)

이 양자수는 상태 벡터의 성분을 지수화합니다.또한 모든 $α$ 는 n차원 집합 $A$ = $A$ × A × $...$ 에 있습니다. $\times 여기$ 서 각 $A$ 는 $α$ 에 대해 허용되는 값의 집합이고, $모든$ $ω$ 는 m차원 " $부피"$ $ω$ $\subseteq$ ℝ에 있으며, $여기$ 서ω=ω ×ω × ... $\times ω$ $및 각$ ω⊆ R은 실수 R의 부분 집합인ω에 $허용$ 되는 값의 집합입니다 $.$ 일반적으로 $n$ 과 $m$ 이 반드시 같은 것은 아닙니다.

예제:

스핀이 있는 3d의 단일 입자에 대해 다른 자유도를 무시하고 데카르트 좌표를 사용하여 z 방향을 따라 입자의 스핀 양자 수에 $대해$ α = $(s)$ 를 취하고 입자의 위치 좌표에 대해 ω = (x, y, z)를 취할 수 있습니다.여기서 $A$ = ${- s$ , -s + 1, ..., s - 1, s}는 허용된 스핀 양자수의 집합이고 ω = R은 3d 위치 공간 전체에 걸쳐 가능한 모든 입자 위치의 집합입니다.
대안적인 선택은 y 방향을 따른 스핀 양자수의 $경우$ $α$ = $(s$ )이고 입자의 운동량 성분의 경우 ω = (p, p, p)입니다.이 경우 $A$ 와 ω은 이전과 동일합니다.

ω⟩ $상태 α$ 에서 {\ $displaystyle$ t}시간에 시스템을 찾을 확률 밀도는 다음과 같습니다.

\rho_{\alpha,\omega }(t)= \Psi({\boldsymbol {\alpha}},{\boldsymbol {\omega },t) ^{2}

$일부$ 또는 모든 가능한 이산 변수 구성에서 $α$ , $D$ ⊆ $A$ , 일부 또는 모든 가능한 연속 변수 구성에서 ω가 있는 시스템을 발견할 확률은 밀도에 대한 합과 적분입니다.

P(t)=\sum _{\boldsymbol {\alpha}}\in D}\int _{C}\rho _{\alpha,\omega }(t)\,\,d^{m}\!{\boldsymbol {\omega}

모든 확률의 합이 1이어야 하므로 정규화 조건

1=\sum_{\boldsymbol {\alpha}}\in A}\int_{\Omega}\rho_{\alpha,\omega}(t)\,d^{m}\!{\boldsymbol {\omega}

시스템이 진화하는 동안 항상 유지되어야 합니다.

정규화 조건에서는 ρ d ω가 무차원이어야 하며, $치수$ 분석에 의해 ψ는 다음과같은 단위를 $가져야$ 합니다(ωω... $ω m) -1/2$ .

온톨로지

파동함수가 실제로 존재하는지, 그리고 그것이 무엇을 나타내는지는 양자역학의 해석에서 주요한 질문입니다.슈뢰딩거, 아인슈타인, 보어와 같은 이전 세대의 많은 유명한 물리학자들은 이 문제에 대해 어리둥절해 했습니다.일부는 코펜하겐 해석의 공식화 또는 변형(예: 보어, 비그너 및 폰 노이만)을 옹호하는 반면 휠러 또는 제인스와 같은 다른 사람들은 더 고전적인 접근^[49] 방식을 채택하고 파동 함수를 관찰자의 마음 속 정보, 즉 현실에 대한 우리의 지식의 척도로 간주합니다.슈뢰딩거, 봄, 에버렛 등 일부 사람들은 파동함수가 객관적이고 물리적인 존재를 가져야 한다고 주장했습니다.아인슈타인은 물리적 실체에 대한 완전한 설명은 추상적인 수학적 공간을 지칭하는 파동함수와는 구별되는 물리적 공간과 시간을 직접적으로 지칭해야 한다고 생각했습니다.^[50]

참고 항목

언급

^ 여기서 함수는 제곱 적분 가능 함수의 공간인 $L$ 의² 원소라고 가정합니다.이 공간의 요소는 더 정확하게는 제곱 적분 가능 함수의 동치 클래스이며, 두 함수가 르베그 측도 $0$ 의 집합에서 다른 경우 동치로 선언됩니다.이는 세미 inner 제품이 아닌 내부 제품(즉, (ψ $,$ ψ) = 0 ⇒ ψ ≡ 0)을 얻기 위해 필요합니다.적분은 르베그 적분으로 간주됩니다.이것은 공간의 완전성을 위해 필수적이며, 따라서 완전한 내적 공간 = 힐베르트 공간을 산출합니다.
^ 양자역학에서는 분리 가능한 힐베르트 공간만 고려되는데, 존의 보조정리(Zorn's Lemma)를 사용하면 선형 대수학(Hamel basis)의 의미에서 정규 기저가 아닌 셀 수 없을 정도로 무한한 샤우더 기저를 인정한다는 의미입니다.
^ 엄밀히 따지면, 그들은 힐베르트 공간에 있지 않습니다.자세한 내용은 스펙트럼 정리를 참조하십시오.
^ ^a ^b "디랙 직교 정규성(Dirac orthonormality)"이라고도 합니다.Griffiths, David J. Introduction to Quantum Mechanics (3rd ed.).
^ 공간 $L$ 에서² 단일 연산자로 보는 푸리에 변환은 고유값 $\pm1,$ ± $i$ 를 갖습니다.고유 벡터는 "Hermite 함수"입니다.에르미트 다항식에 가우시안 함수를 곱한 것입니다.푸리에 변환을 유니터리 변환으로 설명하려면 Byron & Fuller(1992)를 참조하십시오.고유값과 고유값에 대해서는 문제 27장 9절을 참조하십시오.
^ 이 문장을 이해하려면 관측치가 최대 통근 집합의 요소여야 합니다.이를 보기 위해서는, 예를 들어 n-입자계에서 i'번째 입자의 운동량 연산자가 자연계의 어떤 대칭성의 생성자가 아니라는 것을 주목하는 것이 간단한 문제입니다.반면에, 총 운동량은 본질적으로 대칭, 즉 번역 대칭의 발생기입니다.
^ 결과적인 기초는 기술적으로 힐베르트 공간의 수학적 의미에서 기초가 될 수도 있고 아닐 수도 있습니다.예를 들어, 정위치 상태와 정운동량 상태는 제곱 적분이 되지 않습니다.이는 웨이브 패킷을 사용하거나 시스템을 "박스"에 둘러싸면 극복될 수 있습니다.아래의 추가 설명을 참조하십시오.
^ 기술적인 용어로 이는 다음과 같은 방식으로 공식화됩니다.내부 제품은 표준을 생성합니다.이 규범은 차례로 미터법을 유도합니다.이 메트릭이 완료되면 앞서 언급한 한계가 함수 공간에 있습니다.그런 다음 내부 제품 공간을 완전이라고 합니다.완전한 내부 제품 공간은 힐베르트 공간입니다.추상적 상태 공간은 항상 힐베르트 공간으로 간주됩니다.기능 공간에 대한 일치 요구 사항은 자연스러운 요구 사항입니다.추상 상태 공간의 힐베르트 공간 속성은 원래 슈뢰딩거 방정식에 정규화 가능한 해를 형성하는 함수 공간이 힐베르트 공간이라는 관찰에서 추출되었습니다.
^ 나중의 각주에서 설명한 바와 같이, 적분은 르베슈 적분으로 간주되어야 하지만 리만 적분으로는 충분하지 않습니다.
^ 콘웨이 1990.이는 내부 제품, 즉 규범이 보존되고 매핑이 경계를 이루며 연속적인 선형 투영임을 의미합니다.완전성의 속성도 유지됩니다.따라서 이것은 힐베르트 공간의 범주에서 동형 사상의 올바른 개념입니다.
^ 그러한 완화 중 하나는 파동함수가 소볼레프 공간 W에^1,2 속해야 한다는 것입니다.분포의 의미에서 미분 가능하고 기울기가 제곱 적분 가능하다는 것을 의미합니다.이 완화는 디랙 델타 함수와 같이 함수는 아니지만 분포인 전위에 필요합니다.
^ 불연속 함수로 수렴하는 요구 사항을 충족하는 함수의 시퀀스를 쉽게 시각화할 수 있습니다.이를 위해 내부 product space #some example에 주어진 예제를 수정합니다.그러나 이 원소는 $L$ 의² 원소입니다.
^ 예를 들어, 섭동 이론에서는 실제 파동 함수에 근접한 일련의 함수를 구성할 수 있습니다.이 시퀀스는 더 큰 공간에서 수렴하는 것이 보장되지만, 본격적인 힐베르트 공간의 가정 없이는 수렴이 관련 공간의 함수에 대한 것이며 따라서 원래 문제를 해결하는 것이 보장되지 않습니다.
^ 평면파 자유 입자 솔루션과 같이 일부 함수는 제곱 적분이 되지 않습니다. 이전 노트와 아래에 설명된 설명에 필요합니다.
^ 여기: $\sum _{\boldsymbol {\alpha}}\equiv \sum _{\alpha _{1}}\alpha _{2}\ldots,\alpha _{n}}\equiv \sum _{\alpha _{2}}\cdots \sum _{\alpha _{n}$ 는 복수합입니다.

인용

^ ^a ^b ^c 1926년생, 휠러 & 주렉 1983에서 52-55쪽으로 번역됨.
^ ^a ^b 1926년생, 루트비히 1968년 번역, 206-225쪽.여기도.
^ 출생, M. (1954)
^ 1927년생, pp. 354–357.
^ 하이젠베르크 1958, 143쪽.
^ 하이젠베르크, W. (1927/1985/2009)Heisenberg는 Camilleri 2009, p. 71, (Bohr 1985, p. 142)에 의해 번역되었습니다.
^ 머독 1987, 43쪽.
^ 드브로이 1960, 페이지 48.
^ 란다우 & 리프쉬츠 1977, 6쪽.
^ 뉴턴 2002, 19-21쪽.
^ "Planck - A very short biography of Planck". spark.iop.org. Institute of Physics. Retrieved 12 February 2023.
^ C/CS Pys C191:Representations and Wave Functions 》 1. Planck-Einstein Relation E=hv (PDF). EESC Instructional and Electronics Support, University of California, Berkeley. 30 September 2008. p. 1. Retrieved 12 February 2023.
^ 아인슈타인 1916, pp. 47–62, 그리고 거의 동일한 버전의 아인슈타인 1917, pp. 121–128 inter Haar 1967, pp. 167–183.
^ 드브로이 1923, 페이지 507–510, 548, 630
^ Hanle 1977, pp. 606–609.
^ 슈뢰딩거 1926, 1049-1070쪽.
^ 티플러, 모스카 & 프리먼 2008.
^ ^a ^b ^c 와인버그 2013.
^ Young & Freedman 2008, 페이지 1333
^ ^a ^b ^c 1974년 앳킨스.
^ 마틴 & 쇼 2008.
^ 파울리 1927, 601-623쪽..
^ Weinberg(2002)는 양자장이론이 양자역학과 특수상대성을 조화시킬 수 있는 유일한 방법이기 때문에 그렇게 나타난다고 주장합니다.
^ Weinberg (2002) 특히 5장을 참조하십시오. 여기서 이러한 결과의 일부가 도출됩니다.
^ 와인버그 2002 4장
^ 즈비바흐 2009.
^ 양자역학의 응용.
^ 그리피스 2004, 페이지 94.
^ 샹카르 1994, 페이지 117.
^ ^a ^b 그리피스 2004.
^ 트레브스 2006, 페이지 112-125.
^ B. Griffiths, Robert. "Hilbert Space Quantum Mechanics" (PDF). p. 1.
^ 랜드스맨 2009.
^ Sankar 1994, pp. 378–379.
^ 란다우 & 리프쉬츠 1977.
^ Zettili 2009, p. 463.
^ Sakurai, Jun John; Napolitano, Jim (2021). Modern quantum mechanics (3rd ed.). Cambridge: Cambridge University Press. pp. 94–97. ISBN 978-1-108-47322-4.
^ 와인버그 2002 제3장 산란행렬.
^ 과학자와 공학자를 위한 물리학 – 현대 물리학(제6판), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7
^ 그리피스 2008, 페이지 162ff.
^ 와인버그 2002.
^ 와인버그 2002, 3장.
^ 콘웨이 1990.
^ 그리너 & 라인하르트 2008.
^ 1985년 아이스버그 & 레스닉
^ 래 2008.
^ 1974년 Atkins, 258쪽.
^ 디랙 1982.
^ 제인스 2003.
^ 아인슈타인 1998, 682쪽.

일반출처

"Applications of Quantum Mechanics". Lecture notes for the course AP3303. Department of Quantum Nanoscience studies at TU Delft. 2022.
Arons, A. B.; Peppard, M. B. (1965). "Einstein's proposal of the photon concept: A translation of the Annalen der Physik paper of 1905" (PDF). American Journal of Physics. 33 (5): 367. Bibcode:1965AmJPh..33..367A. doi:10.1119/1.1971542.
Atkins, P. W. (1974). Quanta: A Handbook of Concepts. ISBN 978-0-19-855494-3.
Bohr, N. (1985). Kalckar, J. (ed.). Niels Bohr - Collected Works: Foundations of Quantum Physics I (1926 - 1932). Vol. 6. Amsterdam: North Holland. ISBN 978-044453289-3.
Born, M. (1926a). "Zur Quantenmechanik der Stoßvorgange". Z. Phys. 37 (12): 863–867. Bibcode:1926ZPhy...37..863B. doi:10.1007/bf01397477. S2CID 119896026.
Born, M. (1926b). "Quantenmechanik der Stoßvorgange". Z. Phys. 38 (11–12): 803–827. Bibcode:1926ZPhy...38..803B. doi:10.1007/bf01397184. S2CID 126244962.
Born, M. (1927). "Physical aspects of quantum mechanics". Nature. 119 (2992): 354–357. Bibcode:1927Natur.119..354B. doi:10.1038/119354a0.
Born, M. (11 December 1954). "The statistical interpretation of quantum mechanics". Nobel Lecture. Nobel Foundation. 122 (3172): 675–9. doi:10.1126/science.122.3172.675. PMID 17798674.
de Broglie, L. (1923). "Radiations—Ondes et quanta" [Radiation—Waves and quanta]. Comptes Rendus (in French). 177: 507–510, 548, 630. 온라인 사본(프랑스어) 온라인 사본(영문)
de Broglie, L. (1960). Non-linear Wave Mechanics: a Causal Interpretation. Amsterdam: Elsevier – via Internet Archive.
Byron, F. W.; Fuller, R. W. (1992) [First published 1969]. Mathematics of Classical and Quantum Physics. Dover Books on Physics (revised ed.). Dover Publications. ISBN 978-0-486-67164-2 – via Internet Archive.
Camilleri, K. (2009). Heisenberg and the Interpretation of Quantum Mechanics: the Physicist as Philosopher. Cambridge UK: Cambridge University Press. ISBN 978-0-521-88484-6.
Conway, J. B. (1990). A Course in Functional Analysis. Graduate Texts in Mathematics. Vol. 96. Springer Verlag. ISBN 978-0-387-97245-9.
Dirac, P. A. M. (1939). "A new notation for quantum mechanics". Mathematical Proceedings of the Cambridge Philosophical Society. 35 (3): 416–418. Bibcode:1939PCPS...35..416D. doi:10.1017/S0305004100021162. S2CID 121466183.
Dirac, P. A. M. (1982). The principles of quantum mechanics. The international series on monographs on physics (4th ed.). Oxford University Press. ISBN 0-19-852011-5.
Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt". Annalen der Physik (in German). 17 (6): 132–148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607.
Einstein, A. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft Zürich. 18: 47–62.
Einstein, A. (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift (in German). 18: 121–128. Bibcode:1917PhyZ...18..121E.
Einstein, A. (1998). Schilpp, P. A. (ed.). Albert Einstein: Philosopher-Scientist. The Library of Living Philosophers. Vol. VII (3rd ed.). La Salle Publishing Company, Illinois: Open Court. ISBN 978-0-87548-133-3.
Eisberg, Robert Martin; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). John Wiley & Sons. ISBN 978-0-471-87373-0 – via Internet Archive.
Greiner, W.; Reinhardt, J. (2008). Quantum Electrodynamics (4th ed.). springer. ISBN 978-354087560-4.
Griffiths, D. J. (2004). Introduction to Quantum Mechanics (2nd ed.). Essex England: Pearson Education. ISBN 978-013111892-8.
Griffiths, David (2008). Introduction to elementary particles. Wiley-VCH. pp. 162ff. ISBN 978-3-527-40601-2.
ter Haar, D. (1967). The Old Quantum Theory. Pergamon Press. pp. 167–183. LCCN 66029628 – via Internet Archive.
Hanle, P.A. (1977), "Erwin Schrodinger's Reaction to Louis de Broglie's Thesis on the Quantum Theory", Isis, 68 (4): 606–609, doi:10.1086/351880, S2CID 121913205
Heisenberg, W. (1958). Physics and Philosophy: the Revolution in Modern Science. New York: Harper & Row – via Internet Archive.
Jaynes, E. T. (2003). Larry, G. (ed.). Probability Theory: The Logic of Science. Cambridge University Press. ISBN 978-0-521 59271-0.
Landau, L.D.; Lifshitz, E. M. (1977). Quantum Mechanics: Non-Relativistic Theory. Vol. 3 (3rd ed.). Pergamon Press. ISBN 978-0-08-020940-1. 온라인 복사
Landsman, N. P. (2009). "Born Rule and its Interpretation" (PDF). Compendium of Quantum Physics. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-540-70626-7_20. ISBN 978-3-540-70622-9.
Lerner, R.G.; Trigg, G.L. (1991). Encyclopaedia of Physics (2nd ed.). VHC Publishers. ISBN 978-0-89573-752-6 – via Internet Archive.
Ludwig, G. (1968). Wave Mechanics. Oxford UK: Pergamon Press. ISBN 978-0-08-203204-5. LCCN 66-30631 – via Internet Archive.
Martin, B.R.; Shaw, G. (2008). Particle Physics. Manchester Physics Series (3rd ed.). John Wiley & Sons. ISBN 978-0-470-03294-7.
Murdoch, D. (1987). Niels Bohr's Philosophy of Physics. Cambridge UK: Cambridge University Press. ISBN 978-0-521-33320-7 – via Internet Archive.
Newton, R.G. (2002). Quantum Physics: a Text for Graduate Student. New York: Springer. ISBN 978-0-387-95473-8.
Pauli, Wolfgang (1927). "Zur Quantenmechanik des magnetischen Elektrons". Zeitschrift für Physik (in German). 43 (9–10): 601–623. Bibcode:1927ZPhy...43..601P. doi:10.1007/bf01397326. S2CID 128228729.
Peleg, Y.; Pnini, R.; Zaarur, E.; Hecht, E. (2010). Quantum mechanics. Schaum's outlines (2nd ed.). McGraw Hill. ISBN 978-0-07-162358-2.
Rae, A.I.M. (2008). Quantum Mechanics. Vol. 2 (5th ed.). Taylor & Francis Group. ISBN 978-1-5848-89700.
Schrödinger, E. (1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules" (PDF). Physical Review. 28 (6): 1049–1070. Bibcode:1926PhRv...28.1049S. doi:10.1103/PhysRev.28.1049. Archived from the original (PDF) on 17 December 2008.
Shankar, R. (1994). Principles of Quantum Mechanics (2nd ed.). ISBN 978-030644790-7.
Tipler, P. A.; Mosca, G.; Freeman (2008). Physics for Scientists and Engineers – with Modern Physics (6th ed.). ISBN 978-0-7167-8964-2.
Treves, Francois (2006). Topological Vector Spaces, Distributions and Kernels. Mineola, NY: Courier Corporation. ISBN 978-0-486-45352-1.
Weinberg, S. (2002), The Quantum Theory of Fields, vol. 1, Cambridge University Press, ISBN 978-0-521-55001-7 – via Internet Archive
Weinberg, S. (2013), Lectures in Quantum Mechanics, Cambridge University Press, ISBN 978-1-107-02872-2
Wheeler, J.A.; Zurek, W.H. (1983). Quantum Theory and Measurement. Princeton NJ: Princeton University Press.
Young, H. D.; Freedman, R. A. (2008). Pearson (ed.). Sears' and Zemansky's University Physics (12th ed.). Addison-Wesley. ISBN 978-0-321-50130-1.
Zettili, N. (2009). Quantum Mechanics: Concepts and Applications (2nd ed.). ISBN 978-0-470-02679-3.
Zwiebach, Barton (2009). A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.

외부 링크

[29] 여기서 함수는 제곱 적분 가능 함수의 공간인 $L$ 의² 원소라고 가정합니다.이 공간의 요소는 더 정확하게는 제곱 적분 가능 함수의 동치 클래스이며, 두 함수가 르베그 측도 $0$ 의 집합에서 다른 경우 동치로 선언됩니다.이는 세미 inner 제품이 아닌 내부 제품(즉, (ψ $,$ ψ) = 0 ⇒ ψ ≡ 0)을 얻기 위해 필요합니다.적분은 르베그 적분으로 간주됩니다.이것은 공간의 완전성을 위해 필수적이며, 따라서 완전한 내적 공간 = 힐베르트 공간을 산출합니다.

[30] 양자역학에서는 분리 가능한 힐베르트 공간만 고려되는데, 존의 보조정리(Zorn's Lemma)를 사용하면 선형 대수학(Hamel basis)의 의미에서 정규 기저가 아닌 셀 수 없을 정도로 무한한 샤우더 기저를 인정한다는 의미입니다.

[31] 엄밀히 따지면, 그들은 힐베르트 공간에 있지 않습니다.자세한 내용은 스펙트럼 정리를 참조하십시오.

[:0-32] "디랙 직교 정규성(Dirac orthonormality)"이라고도 합니다.Griffiths, David J. Introduction to Quantum Mechanics (3rd ed.).

[35] 공간 $L$ 에서² 단일 연산자로 보는 푸리에 변환은 고유값 $\pm1,$ ± $i$ 를 갖습니다.고유 벡터는 "Hermite 함수"입니다.에르미트 다항식에 가우시안 함수를 곱한 것입니다.푸리에 변환을 유니터리 변환으로 설명하려면 Byron & Fuller(1992)를 참조하십시오.고유값과 고유값에 대해서는 문제 27장 9절을 참조하십시오.

[47] 이 문장을 이해하려면 관측치가 최대 통근 집합의 요소여야 합니다.이를 보기 위해서는, 예를 들어 n-입자계에서 i'번째 입자의 운동량 연산자가 자연계의 어떤 대칭성의 생성자가 아니라는 것을 주목하는 것이 간단한 문제입니다.반면에, 총 운동량은 본질적으로 대칭, 즉 번역 대칭의 발생기입니다.

[48] 결과적인 기초는 기술적으로 힐베르트 공간의 수학적 의미에서 기초가 될 수도 있고 아닐 수도 있습니다.예를 들어, 정위치 상태와 정운동량 상태는 제곱 적분이 되지 않습니다.이는 웨이브 패킷을 사용하거나 시스템을 "박스"에 둘러싸면 극복될 수 있습니다.아래의 추가 설명을 참조하십시오.

[51] 기술적인 용어로 이는 다음과 같은 방식으로 공식화됩니다.내부 제품은 표준을 생성합니다.이 규범은 차례로 미터법을 유도합니다.이 메트릭이 완료되면 앞서 언급한 한계가 함수 공간에 있습니다.그런 다음 내부 제품 공간을 완전이라고 합니다.완전한 내부 제품 공간은 힐베르트 공간입니다.추상적 상태 공간은 항상 힐베르트 공간으로 간주됩니다.기능 공간에 대한 일치 요구 사항은 자연스러운 요구 사항입니다.추상 상태 공간의 힐베르트 공간 속성은 원래 슈뢰딩거 방정식에 정규화 가능한 해를 형성하는 함수 공간이 힐베르트 공간이라는 관찰에서 추출되었습니다.

[52] 나중의 각주에서 설명한 바와 같이, 적분은 르베슈 적분으로 간주되어야 하지만 리만 적분으로는 충분하지 않습니다.

[53] 콘웨이 1990.이는 내부 제품, 즉 규범이 보존되고 매핑이 경계를 이루며 연속적인 선형 투영임을 의미합니다.완전성의 속성도 유지됩니다.따라서 이것은 힐베르트 공간의 범주에서 동형 사상의 올바른 개념입니다.

[57] 그러한 완화 중 하나는 파동함수가 소볼레프 공간 W에^1,2 속해야 한다는 것입니다.분포의 의미에서 미분 가능하고 기울기가 제곱 적분 가능하다는 것을 의미합니다.이 완화는 디랙 델타 함수와 같이 함수는 아니지만 분포인 전위에 필요합니다.

[59] 불연속 함수로 수렴하는 요구 사항을 충족하는 함수의 시퀀스를 쉽게 시각화할 수 있습니다.이를 위해 내부 product space #some example에 주어진 예제를 수정합니다.그러나 이 원소는 $L$ 의² 원소입니다.

[60] 예를 들어, 섭동 이론에서는 실제 파동 함수에 근접한 일련의 함수를 구성할 수 있습니다.이 시퀀스는 더 큰 공간에서 수렴하는 것이 보장되지만, 본격적인 힐베르트 공간의 가정 없이는 수렴이 관련 공간의 함수에 대한 것이며 따라서 원래 문제를 해결하는 것이 보장되지 않습니다.

[61] 평면파 자유 입자 솔루션과 같이 일부 함수는 제곱 적분이 되지 않습니다. 이전 노트와 아래에 설명된 설명에 필요합니다.

[63] 여기: $\sum _{\boldsymbol {\alpha}}\equiv \sum _{\alpha _{1}}\alpha _{2}\ldots,\alpha _{n}}\equiv \sum _{\alpha _{2}}\cdots \sum _{\alpha _{n}$ 는 복수합입니다.

[Born_1926_A-1] 1926년생, 휠러 & 주렉 1983에서 52-55쪽으로 번역됨.

[Born_1926_B-2] 1926년생, 루트비히 1968년 번역, 206-225쪽.여기도.

[3] 출생, M. (1954)

[FOOTNOTEBorn1927354–357-4] 1927년생, pp. 354–357.

[FOOTNOTEHeisenberg1958143-5] 하이젠베르크 1958, 143쪽.

[6] 하이젠베르크, W. (1927/1985/2009)Heisenberg는 Camilleri 2009, p. 71, (Bohr 1985, p. 142)에 의해 번역되었습니다.

[FOOTNOTEMurdoch198743-7] 머독 1987, 43쪽.

[FOOTNOTEde_Broglie196048-8] 드브로이 1960, 페이지 48.

[FOOTNOTELandauLifshitz19776-9] 란다우 & 리프쉬츠 1977, 6쪽.

[FOOTNOTENewton200219–21-10] 뉴턴 2002, 19-21쪽.

[11] "Planck - A very short biography of Planck". spark.iop.org. Institute of Physics. Retrieved 12 February 2023.

[12] C/CS Pys C191:Representations and Wave Functions 》 1. Planck-Einstein Relation E=hv (PDF). EESC Instructional and Electronics Support, University of California, Berkeley. 30 September 2008. p. 1. Retrieved 12 February 2023.

[13] 아인슈타인 1916, pp. 47–62, 그리고 거의 동일한 버전의 아인슈타인 1917, pp. 121–128 inter Haar 1967, pp. 167–183.

[FOOTNOTEde_Broglie1923507–510,_548,_630-14] 드브로이 1923, 페이지 507–510, 548, 630

[FOOTNOTEHanle1977606–609-15] Hanle 1977, pp. 606–609.

[FOOTNOTESchrödinger19261049–1070-16] 슈뢰딩거 1926, 1049-1070쪽.

[FOOTNOTETiplerMoscaFreeman2008-17] 티플러, 모스카 & 프리먼 2008.

[FOOTNOTEWeinberg2013-18] 와인버그 2013.

[FOOTNOTEYoungFreedman20081333-19] Young & Freedman 2008, 페이지 1333

[FOOTNOTEAtkins1974-20] 1974년 앳킨스.

[FOOTNOTEMartinShaw2008-21] 마틴 & 쇼 2008.

[FOOTNOTEPauli1927601–623.-22] 파울리 1927, 601-623쪽..

[23] Weinberg(2002)는 양자장이론이 양자역학과 특수상대성을 조화시킬 수 있는 유일한 방법이기 때문에 그렇게 나타난다고 주장합니다.

[24] Weinberg (2002) 특히 5장을 참조하십시오. 여기서 이러한 결과의 일부가 도출됩니다.

[25] 와인버그 2002 4장

[FOOTNOTEZwiebach2009-26] 즈비바흐 2009.

[FOOTNOTEApplications_of_Quantum_Mechanics-27] 양자역학의 응용.

[FOOTNOTEGriffiths200494-28] 그리피스 2004, 페이지 94.

[FOOTNOTEShankar1994117-33] 샹카르 1994, 페이지 117.

[FOOTNOTEGriffiths2004-34] 그리피스 2004.

[FOOTNOTETreves2006112-125-36] 트레브스 2006, 페이지 112-125.

[:0-37] B. Griffiths, Robert. "Hilbert Space Quantum Mechanics" (PDF). p. 1.

[FOOTNOTELandsman2009-38] 랜드스맨 2009.

[FOOTNOTEShankar1994378–379-39] Sankar 1994, pp. 378–379.

[FOOTNOTELandauLifshitz1977-40] 란다우 & 리프쉬츠 1977.

[FOOTNOTEZettili2009463-41] Zettili 2009, p. 463.

[42] Sakurai, Jun John; Napolitano, Jim (2021). Modern quantum mechanics (3rd ed.). Cambridge: Cambridge University Press. pp. 94–97. ISBN 978-1-108-47322-4.

[43] 와인버그 2002 제3장 산란행렬.

[44] 과학자와 공학자를 위한 물리학 – 현대 물리학(제6판), P. A. Tipler, G. Mosca, Freeman, 2008, ISBN 0-7167-8964-7

[FOOTNOTEGriffiths2008162ff-45] 그리피스 2008, 페이지 162ff.

[FOOTNOTEWeinberg2002-46] 와인버그 2002.

[FOOTNOTEWeinberg2002Chapter_3-49] 와인버그 2002, 3장.

[FOOTNOTEConway1990-50] 콘웨이 1990.

[FOOTNOTEGreinerReinhardt2008-54] 그리너 & 라인하르트 2008.

[FOOTNOTEEisbergResnick1985-55] 1985년 아이스버그 & 레스닉

[FOOTNOTERae2008-56] 래 2008.

[FOOTNOTEAtkins1974258-58] 1974년 Atkins, 258쪽.

[FOOTNOTEDirac1982-62] 디랙 1982.

[FOOTNOTEJaynes2003-64] 제인스 2003.

[FOOTNOTEEinstein1998682-65] 아인슈타인 1998, 682쪽.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[nb 2]

[nb 4]

[30]

[nb 5]

[31]

[32]

[34]

[35]

[36]

[38]

[39]

[40]

[41]

[nb 6]

[nb 7]

[42]

[43]

[nb 8]

[nb 9]

[nb 10]

[44]

[45]

[46]

[nb 11]

[47]

[nb 12]

[nb 13]

[nb 14]

[48]

[49]

[50]

v t 양자역학
배경	서론 역사 타임라인 고전역학 구양자론 용어집
펀더멘털	모태규칙 브라켓 표기법 상보성 밀도행렬 에너지 준위 지반상태 들뜬 상태 퇴화 수준 영점 에너지 얽힘 해밀토니안 방해다 디코히어런스 측정. 비국소성 양자 상태 중첩 터널링 산란설 양자역학에서의 대칭성 불확실성 파동함수 쓰러짐 파동-입자 이중성
제형	제형 하이젠베르크 상호작용 행렬역학 슈뢰딩거 경로적분공식 위상공간
방정식	디랙 클라인고든 파울리 뤼드베르크 슈뢰딩거
해석	베이지안 일관 이력 코펜하겐 드브로이-봄 앙상블 숨은 변수 현지의 초결정론 다세계 대물붕괴 양자논리학 관계형 거래적 폰 노이만-비그너
실험	벨 테스트 다비송-독일 지연선택 양자지우개 더블슬릿 프랭크-헤르츠 마하-젠더 간섭계 Elitzur–Vaidman 포퍼 양자지우개 슈테른-게를라흐 휠러의 지연된 선택
과학	양자생물학 양자화학 양자 혼돈 양자우주론 양자미분학 양자역학 양자기하학 양자계측문제 양자마인드 양자 확률 미적분학 양자 시공간
기술	양자 알고리즘 양자증폭기 양자 버스 양자 세포 오토마타 양자 유한 오토마타 양자 채널 양자 회로 양자복잡성이론 양자전산 타임라인 양자암호학 양자전자학 양자오류보정 양자영상 양자영상처리 양자정보 양자키분포 양자논리학 양자 논리 게이트 양자기계 양자기계학습 양자 메타물질 양자계량학 양자망 양자신경망 양자광학 양자 프로그래밍 양자감지 양자 시뮬레이터 양자 순간이동
확장	양자 변동 카시미르 효과 양자통계역학 양자장이론 역사 양자중력 상대론적 양자역학
관련된	슈뢰딩거의 고양이 대중문화에 있어서 위그너의 친구 EPR 역설 양자 신비주의
카테고리 물리 포털 커먼즈

Search